基于BPNN-EMD-LSTM组合模型的城市短期燃气负荷预测

陈 川，陈冬林，何李凯

(武汉理工大学电子商务与智能服务研究中心，湖北 武汉 430070)

随着我国清洁能源政策的大力推行，天然气在一次能源消费结构中的占比不断增长，安全、稳定的天然气供应极为重要[1-2]。对应于快速增长的天然气需求，天然气产能的严重不足已连续多年造成我国区域性“气荒”。在此背景下，为增强天然气保障能力，管道天然气线上竞价交易于2017年9月在上海石油天然气交易中心正式开启。管道气竞价交易机制的出现为燃气公司解决区域性“气荒”提供契机的同时，也向其提出了新的挑战：在原有燃气采购合同的基础上，短期内购气过量将造成额外的存储成本；短期内购气不足则难以解决“气荒”，保障供气。因此，寻求一种准确、可行的城市短期燃气负荷预测模型和方法具有重要的理论价值与现实意义。

在城市燃气负荷预测方面，现有的研究可分为两个方向：①研究城市燃气负荷的成因，从影响因素着手提高预测模型的解释能力；②研究城市燃气负荷多元化预测方法，从不同角度分析和利用已知信息，提高预测模型的性能。在研究城市燃气负荷的成因方面，常见的影响因素包括气象因素、经济因素、社会因素等[3-4]。如顾婷婷等[5]从气象因素出发，深入研究了城市燃气负荷与日平均气温、日平均气压、相对湿度等主要气象因子的关系；周伟国等[6]通过计算判断得出城市燃气负荷具有与气象参数、经济指标等类似的混沌性质；李谦益等[7]认为气温累计效应对城市燃气负荷具有较大的影响，并提出气温修正公式进行验证。在研究城市燃气负荷多元化预测方法方面，常见的改进预测方法为预处理数据、优化单一模型和建立组合模型等[8-9]。如张超等[10]从数据预处理方法和不同时段的用气特点两个方面，分析了提高城市燃气日负荷预测准确性的方法，并建立了支持向量机(SVM)模型进行验证；龚承柱等[11]抛却外界因素的影响，通过对原始数据进行分解(EMD)、重构(PSR)，建立了基于最小二乘支持向量机(LSSVM)的组合预测模型，对城市燃气管网短期负荷进行了时序预测；Yu等[12]利用遗传算法对城市短期燃气负荷的BP神经网络进行改进，加快了网络收敛速度；Rodger等[13]建立了模糊最近邻神经网络统计模型，能够很好地拟合城市燃气日负荷曲线。然而从预测目标的角度来看，以上研究的差异可归结为预测步长与预测精度的不同，现有文献关于“气荒”环境下半月步长的高精度城市燃气负荷预测的研究较为稀少。考虑城市燃气负荷的混沌性，其历史数据具有非线性和高随机性的特点，单一模型无法较好地解释除主要影响因素以外其他因素的影响，针对此类问题，考虑借鉴EMD算法处理非线性、非平稳数据的优势[14-15]，运用EMD方法对主要影响因素以外的其他因素影响下的数据进行分解。

本文通过对燃气日负荷历史特征的分析，剥离开燃气负荷的主要影响因素与其他影响因素。先以温度、日期属性作为主要影响因素，利用BPNN模型捕捉燃气日负荷的主要特征，其他因素的影响则体现在BPNN模型预测产生的非线性残差中；然后运用EMD-LSTM模型进行拟合，将BPNN模型与EMD-LSTM模型相结合得到组合预测模型，并以某城市民用类燃气日负荷为研究对象进行了实证分析，结果表明：BPNN-EMD-LSTM组合预测模型具有较好的预测效果，能够为燃气公司短期购气决策提供科学依据。

1 数据来源与特征分析

本文以我国某城市民用燃气日负荷为研究对象，根据2015年1月1日至2017年4月30日之间851天的城市燃气日负荷数据，对2017年5月1日起未来15天的城市燃气日负荷进行了预测。该城市原始燃气日负荷数据，见图1。

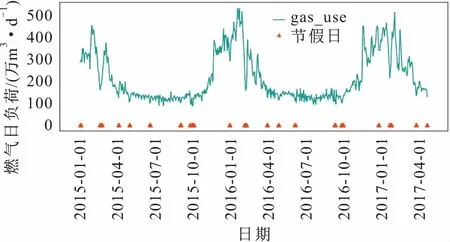
图1 某城市燃气日负荷的变化曲线Fig.1 Change curve of the daily natural gas load of a city 注：图中实线反映了燃气日负荷的变化；“▲”代表该天为我国法定节假日；节假日及历史天气数据从“中国天气网”获取。

由图1可见，该市一年内4月中旬至10月底燃气日负荷波动幅度较小，其余时段燃气日负荷存在剧烈波动，燃气日负荷整体偏高，初步判断燃气日负荷与温度有较强的相关性；另外，该市燃气日负荷在节假日期间显著降低，判断节假日的出现会在一定程度上影响燃气的日负荷。

2 基于BPNN-EMD-LSTM的组合预测模型建立

组合预测模型的基本思路是将燃气负荷的影响因素拆分为主要影响因素和其他影响因素两类，并由BPNN模型计算主要影响因素与燃气负荷的映射关系，由EMD-LSTM模型预测受其他因素影响的时序残差，并将两部分预测结果结合以完成对燃气负荷的组合预测。下面对BPNN-EMD-LSTM组合预测模型中的具体方法进行分析。

2.1 BP神经网络(BPNN)

BP神经网络(Back Propagation Neural Network,BPNN)是一种按误差逆向传播算法训练的多层前馈神经网络。作为一种全连接神经网络，BPNN模型具有很强的计算能力和复杂的映射能力，能够对大量非结构性、非精确性规律进行自适应训练，主要应用于模式识别、函数逼近等[16]。其原理和方法如下：

对一个三层BP神经网络，假定网络有n个输入xi(i=1,2,…,n)，m个输出yi(i=1,2,…,m)，该神经网络计算可分为工作信号的正向传递、误差信号的反向传递两个过程。

工作信号的正向传递：设节点i和节点j间的权值为ωij，节点j的阈值为bj，节点的输入为xi，节点的输出为xj，则:

(1)

xj=f(Sj)

(2)

式中：Sj为节点j的所有输入信号在权值、阈值作用下产生的待激活信号;f(Sj)为激活函数，一般根据数据内在规律的不同按需选择。

误差信号的反向传递：假定每一个样本所对应的二次型误差函数为

(3)

其中，dk为网络第k个节点的期望输出;yk为网络的实际输出。

BPNN模型训练的目的在于反复修正权值和阈值使总的误差函数值E最小，根据梯度下降法计算，则:

(4)

(5)

式中：η1、η2分别为权值与阈值的学习速率，取值在0～1之间。

对于训练完成的BPNN，权值和阈值固定，进行预测时只需将数据按规范形式输入网络，即可自动计算得到相应的预测结果。

2.2 经验模态分解(EMD)

经验模态分解(Empirical Mode Decomposition,EMD)是一种处理非线性、非平稳时变序列的方法，该方法根据数据自身的时间尺度特征自适应分解信号，被认为是对以平稳和线性假设为基础的傅里叶分析和小波分析的突破[17]。EMD算法的筛选过程是将复杂时序数据分解为有限个本征模函数(Intrinsic Mode Function,IMF)，分解得到的IMF分量包含了原数据在不同时间尺度的波动信息。

对一给定原始时序样本数据x(t)，首先计算x(t)上的局部最大值、最小值，分别对局部最大值、最小值进行插值拟合得到原始数据x(t)的上下包络xmax(t)和xmin(t)序列，然后计算上下包络序列的均值，得到均值序列m1(t)：

(6)

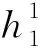
(7)

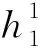
(8)

这里SD为筛分门限，一般取值在0.2～0.3之间较为合适。从x(t)中减去c1(t)，得到移除最高频成分的残差序列r1(t)=x(t)-c1(t)。重复上述筛选过程，得到后续IMF分量，直至cn(t)小于预定误差或rn(t)是单调函数，终止模态分解过程。至此，原始序列x(t)可由n阶IMF分量和残差rn(t)表示：

(9)

2.3 长短期记忆(LSTM)神经网络

长短期记忆(Long Short-Term Memory,LSTM)神经网络最早由Hochreiter和Schmidhuber于1997年提出[18]，是一种特定形式的循环神经网络。LSTM神经网络的计算过程同样可分为前向传播计算和误差反向传播更新两步，不同的是LSTM神经网络由众多记忆单元组成，记忆单元中应用多种控制器的形式对上一单元输出、当前单元输入、上一单元状态进行判断，控制丢弃或增加信息，从而实现遗忘或记忆功能。以一个记忆单元为例，LSTM神经网络的前向传播计算过程见图2。

图2 LSTM神经网络记忆单元的前向传播计算过程Fig.2 Forward propagation computation process of the memory unit of the LSTM neural network

在LSTM神经网络的记忆单元中，“遗忘门”是以本单元的输入xt与上一单元的输出ht-1为输入的“sigmoid”激活函数，“遗忘门”输出ft的值域为[0,1]，LSTM神经网络记忆单元通过ft来控制上一单元状态Ct-1被遗忘的程度。ft表示如下：

ft=σ(Wf·[ht-1xt]+bf)

(10)

式中：Wf、bf为“遗忘门”线性关系的系数和偏置；σ为“sigmoid”激活函数。

(11)

it=σ(Wi·[ht-1,xt]+bi)

(12)

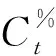
(13)

式中：Wc、bc，Wi、bi为“输入门”线性关系的系数和偏置；“*”表示按元素乘。

在LSTM神经网络的记忆单元中，“输出门”用于控制当前的单元状态Ct有多少被过滤掉。将单元状态Ct通过“tanh”函数激活后，通过“输出门”输出结果ot来控制单元状态被过滤的程度。用数学表达式可表示如下：

ot=σ(Wa·[ht-1,xt]+ba)

(14)

ht=ot*tanh(Ct)

(15)

式中：Wo、bo为“输出门”线性关系的系数和偏置。

LSTM神经网络的反向传播过程与RNN相同，使用BPTT算法(Back Propagation Through Time)对单元状态和“遗忘门”等部分进行更新。

3 基于BPNN-EMD-LSTM组合模型的城市短期燃气负荷预测流程

城市燃气管网负荷变化受多种因素，例如气温突变、节假日以及经济发展等因素的影响，若预测时全部考虑在内，不仅增加模型的复杂度，也会降低模型的性能，因此需将影响因素加以区分，并通过模型分别加以解释。基于BPNN-EMD-LSTM组合模型对城市短期燃气负荷进行预测的流程，详见图3。

图3 基于BPNN-EMD-LSTM组合模型的城市短期燃气负荷预测流程Fig.3 Diagram of the short-term forecast process of urban natural gas load based on the BPNN-EMD-LSTM combined model

基于BPNN-EMD-LSTM组合模型的城市短期燃气负荷预测步骤如下：

(1) BPNN训练与预测。选择与城市燃气日负荷有较强相关性的外界因素为输入，划分训练集、预测集，依据经验设定隐层层数h、隐层节点数l以及激活函数f，按梯度下降算法对模型进行有监督训练，分别计算训练集预测值与实际值的残差Ye以及预测集的预测值Yb。

(2) 残差序列分解。采用EMD分解流程，将BPNN训练集预测残差Ye分解为n组不同频率的本征模态分量{IMF1,IMF2,…,IMFn}和残差项rn。

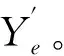
(16)

4 实证分析

4. 1 输入变量的确定

根据对图1的分析，考虑计算日期属性Dt、日平均气温Tt与燃气日负荷Yt间的相关性，引入虚拟变量Dt表示日期属性，考虑节假日和周末休息日对人活动习惯的影响不同，日期属性Dt可表示为

通过计算得到日平均气温Tt与燃气日负荷Yt的Pearson相关系数为-0.864 84，两者有极强的负相关性，日平均气温Tt可作为主要影响因素由BPNN加以解释；日期属性Dt与燃气日负荷Yt的Pearson相关系数仅为-0.119 8，两者相关性似乎不明显，但结合对图1的分析可知，节假日时段内燃气日负荷Yt同样会急剧下降，因此决定采用日期属性Dt作为主要影响因素中的一项进行燃气日负荷预测。

4.2 BPNN的练训与预测

由上述分析可知，BPNN有日期属性Dt和日平均气温Tt两个输入，据此建立两输入单输出的BPNN模型，隐层层数h、隐层神经元个数l采用试错法在网络学习中优选，这里选取h=2、l1=12、l2=3，并采用“tanh”函数作为神经元的激活函数。BPNN训练时将2015年1月1日至2017年4月30日共851天的数据作为训练集，以均方误差(MSE)作为损失函数，设定学习步长η=0.1，最大循环次数n=30 000，以梯度下降法对隐层权重ωl1、ωl2进行训练。

分别将训练集与预测集输入训练完成后的网络，计算得到训练集的预测值Ybtrain与预测集的预测值Yb，并计算训练集预测的残差：Ye=Y-Ybtrain。BPNN模型的预测结果与残差序列见图4。

图4 BPNN模型的预测结果与残差序列图Fig.4 Diagram of BPNN forecast results and the residual sequences

4.3 残差的EMD-LSTM时序预测

将BPNN模型预测所得的残差按EMD流程分解，获得具有原始残差序列不同波动尺度信息的本征模态分量IMF1～IMF13，考虑到对IMF分量的重构一般根据经验主观确定重构方法，不适用于对残差项分解后重构，这里选择保留所有分量信号，并针对不同IMF分量分别建立LSTM时序预测模型进行预测。

对于13个本征模态分量IMF1～IMF13，根据预测需要，建立LSTM时序预测模型时统一设定LSTM神经网络的训练方式为：通过历史30 d的数据学习未来15 d的数据规律，因此将长度为851的残差序列整合为长度为45的807条数据，归一化后组合成一个807×45的矩阵，即：

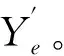
4. 4 预测结果分析

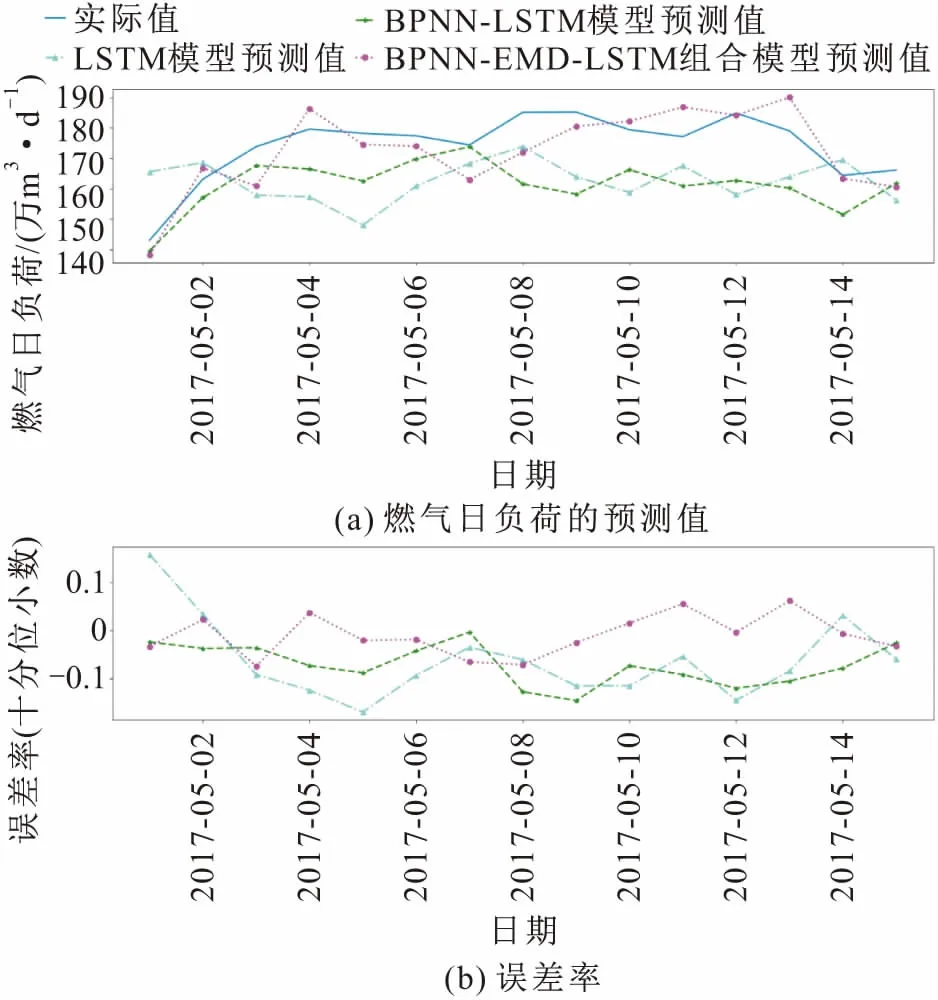
图5 3种预测模型的燃气日负荷预测值与误差率Fig.5 Forecast values and error rates of the three models for forcast of natural gas daily load

由图5可见，BPNN-EMD-LSTM组合预测模型具有很好的预测效果，即使在“五一”节假日期间也能准确地捕捉燃气负荷的变化；BPNN-LSTM预测模型能较准确地预测出“五一”节假日期间燃气日负荷；而LSTM预测模型的预测效果相比而言较差。3种预测模型的预测效果比较见表1。

表1 3种预测模型的预测效果比较

由表1可知，BPNN-EMD-LSTM组合预测模型的相关系数(R)更接近1，从侧面反映出该组合预测模型能够很好地预测出燃气日负荷的整体变化趋势，且另外3个预测评价指标即平均绝对误差(MAPE)、最大百分比误差(MaxPE)和均方根误差(RMSE)都比LSTM模型和BPNN-LSTM模型小很多，说明该组合模型的预测效果比单个LSTM模型和BPNN-LSTM模型更好；然而这并不代表每天的预测结果都是组合模型最好，如1日、7日、15日BPNN-LSTM模型的预测误差反而最小，而LSTM模型在8日和11日具有最好的预测精度。但总体上看，本文所建立的BPNN-EMD-LSTM组合模型具有更好、更稳健的预测效果。

5 结 论

天然气是我国推进能源生产和消费革命，实现主体能源绿色低碳更替的重要基础，“气荒”环境下精准预测半月步长的城市燃气负荷，对燃气管理部门通过天然气竞价交易机制补充购气，完成“保供”任务尤为重要。本文探讨了当前国内外燃气负荷预测的方法，并以某城市民用类燃气日负荷为研究对象，通过对该市燃气日负荷历史特征进行分析，剥离出燃气负荷的主要影响因素与其他影响因素，在此基础上建立了BPNN-EMD-LSTM组合预测模型对该市燃气日负荷的变化加以解释。实证结果表明：该组合预测模型能很好地拟合并预测城市燃气日负荷，比单一的LSTM模型和BPNN-LSTM模型具有更有效、更稳健的预测效果。当然，本文也存在残差序列与其他影响因素间关系不明确的问题，因此在今后的研究中需要做更深入的探讨。总体上来看，通过本文实证研究和预测模型的对比分析表明，类似BPNN-EMD-LSTM的组合模型比较适合城市短期燃气日负荷需求预测，为相关研究提供了一种新的视角，在现实中具有良好的应用前景。