固贴式薄膜体声波传感器的仿真分析
吴永盛,苏淑靖,翟成瑞,马晓鑫,袁财源
(中北大学,电子测试技术重点实验室,仪器科学与动态测试教育部重点实验室,山西太原 030051)
0 引言
随着无线通信系统和射频技术的飞速发展,工作在射频波段传感器的微型化、集成化、低功耗及高性能越来越受到人们的重视。相对于传统的介质传感器和声表面波传感器而言,体声波传感器(BAWR)具有工作频率高、容易实现GHz的水平、品质因数高、尺寸小、可与集成电路CMOS工艺兼容、功率容量大等优点,满足现代通讯的许多苛刻要求,因此BAWR逐渐成为科研工作者的关注热点[1]。布拉格反射栅薄膜体声波传感器(BAW-SMR)作为BAWR的一种,其关键在于BAW-SMR有由高/低声阻抗材料交替叠加形成的布拉格反射栅结构,提高了传感器的机械强度,在后期划片及封装的过程中显著减少了因操作不当造成的物理损伤[2]。
目前业内常用的高声阻抗材料主要是一些高杨氏模量、高硬度的材料,常用的低声阻抗材料为SiO2[3],SiO2的声阻抗值小,成本低廉,已经被半导体工艺广泛接受。2008年,Milyutin E等提出了以AlN作高声阻抗材料,SiO2作低声阻抗材料[4];2011年,陆晓欣等提出了以ta-C作为高声阻抗材料,以SiO2作为低声阻抗材料[5];从减少薄膜种类和简化工艺难度的角度考虑,采用的声阻抗材料和压电薄膜材料相同可以减少工艺复杂度;另外,AlN/SiO2的阻抗比相对于ta-C/AlN的阻抗比小很多,理论上,高/低声阻抗材料的比值越大,布拉格反射栅的效果越好。
本文采用ta-C作高声阻抗材料,AlN作低声阻抗材料,AlN作压电薄膜材料,Mo作电极材料,建立BAW-SMR传感器模型,利用COMSOL Multiphysics对BAW-SMR传感器进行仿真分析,分析不同布拉格反射栅对数对BAW-SMR传感器性能的影响,并仿真了电极边长尺寸及厚度对传感器特征频率的影响。
1 BAWR传感器的工作原理
根据BAWR传感器中声波的传播模式不同,可以将BAWR传感器分为纵波模式BAWR传感器和剪切波模式BAWR传感器。如图1所示,纵波模式BAWR传感器结构是典型的三明治结构,由上、下电极以及压电薄膜构成。

图1 纵波模式BAWR的三明治结构
其工作原理如下:外加交流电压作用于三明治结构的电极,在外加交流电压的作用下,压电薄膜由于具有逆压电效应会产生周期性的机械形变,从而在压电薄膜内激励出纵向传播的体声波,当体声波的频率与压电薄膜的固有特征频率相同时发生谐振,最终发生谐振的声信号通过压电体的压电效应以电信号的形式输出;当BAWR传感器受外界作用时,压电薄膜材料的杨氏模量会发生变化,导致体声波在压电薄膜内的传播速度发生变化,进而导致传感器的谐振频率发生变化,通过测量谐振频率的变化量,就能计算出被测物理量的大小[6]。
如图2所示,根据声波的传输原理,向上传播的声波在上电极介质/空气界面上反射,向下传播的声波则进入到布拉格反射栅中,布拉格反射栅是由介质内声波1/4波长厚的高/低声阻抗材料交替叠加形成的,在每个高/低声阻抗材料的交界面,声波被大量反射,反射波会以合适的相位叠加,形成主驻波,最终达到几乎全反射的效果。

图2 BAW-SMR传感器简单示意图
(1)
式中:fp为并联谐振频率;fs为串联谐振频率[7]。
2 BAW-SMR传感器模型的建立及仿真
理想情况下,BAWR传感器的谐振频率为
f0=v/(2d)
(2)
式中:v为声波在压电材料中的传播速度;d压电薄膜的厚度[8]。
本次设计的压力传感器的谐振频率为4 GHz,纵波在AlN材料中的传播速度为6 720 m/s,由式(2)可以计算出所需压电薄膜的厚度为840 nm,在COMSOL Multiphysics中绘制BAW-SMR的几何结构,各层膜的材料及厚度如表1所示。

表1 传感器各膜层的材料及厚度
按照图2建模完成后,对各层膜设置材料并添加材料属性参数如表2所示。

表2 材料属性
在各层膜的材料和尺寸都确定之后,对几何结构添加物理场并设置边界条件。物理场分为固体力学物理场和静电学物理场2部分,其中固体力学物理场可用于分析计算零件和子系统在载荷作用下产生的变形;静电学物理场可用于分析计算零件和子系统在外加电压作用下的电势及电荷分布情况。分别在每个物理场设置相应的边界条件,固体力学场的边界条件为:在传感器左右两侧添加固定约束,使得传感器左右两侧的变形为零,另外在上电极上表面和压电薄膜上表面添加边界载荷,使传感器均匀受力;静电学的边界条件为:上电极加0.3 V交流电压,下电极接地,使传感器中声波的传播方式为纵波模式。
在用COMSOL Multiphysics对模型进行有限元仿真计算之前,还需对结构进行网格划分,在划分网格的过程中,网格的疏密度直接影响仿真的结果,所以网格划分要兼顾计算量和精度,在计算结果不失真的前提下尽量减小计算量。完成网格划分后,添加研究进行仿真计算:在特征频率研究中设置特征频率搜索范围和所需特征频率数;在频域研究中设置频率搜索范围。为了得到更为精确的结果,可以在频域研究中加大频率搜索的范围。
3 仿真结果与分析
通过对BAW-SMR传感器的二维仿真计算,得到BAW-SMR传感器在不同布拉格反射栅对数下的导纳特性曲线,如图3所示。通过分析可以得到,BAW-SMR传感器的特征频率并没有随着布拉格反射层数的改变而变化,特征频率为3.258 GHz。

(a)3对

(b)4对

(c)5对
在得到传感器的导纳曲线图以及特征频率后,对特征频率研究进行仿真扫频范围设置并进行有限元计算,先进行大范围的扫频分析,在接近特征频率值附近加密频率间隔,得到接近共振点的形变位移分布(取4对布拉格反射栅的形变位移)如图4所示。

图4 BAW-SMR传感器形变位移图
由图4可知,当特征频率为3.258 GHz的时候,BAW-SMR的形变位移有最优值,与导纳图得出的结果一致。传感器中心位置的形变位移有最大值,由中心向两端,形变位移以指数形式递减;在电极覆盖范围之外的位置,传感器的形变位移近似为零,这表明传感器的形变位移受电极位置的影响。图4所示最大位移为662 nm,可见压电薄膜材料的最大位移在材料的应变范围之内,理论上证明了传感器在该频率下可以正常工作。
通过对BAW-SMR传感器进行有限元仿真分析,计算得到传感器的阻抗特性曲线如图5所示。
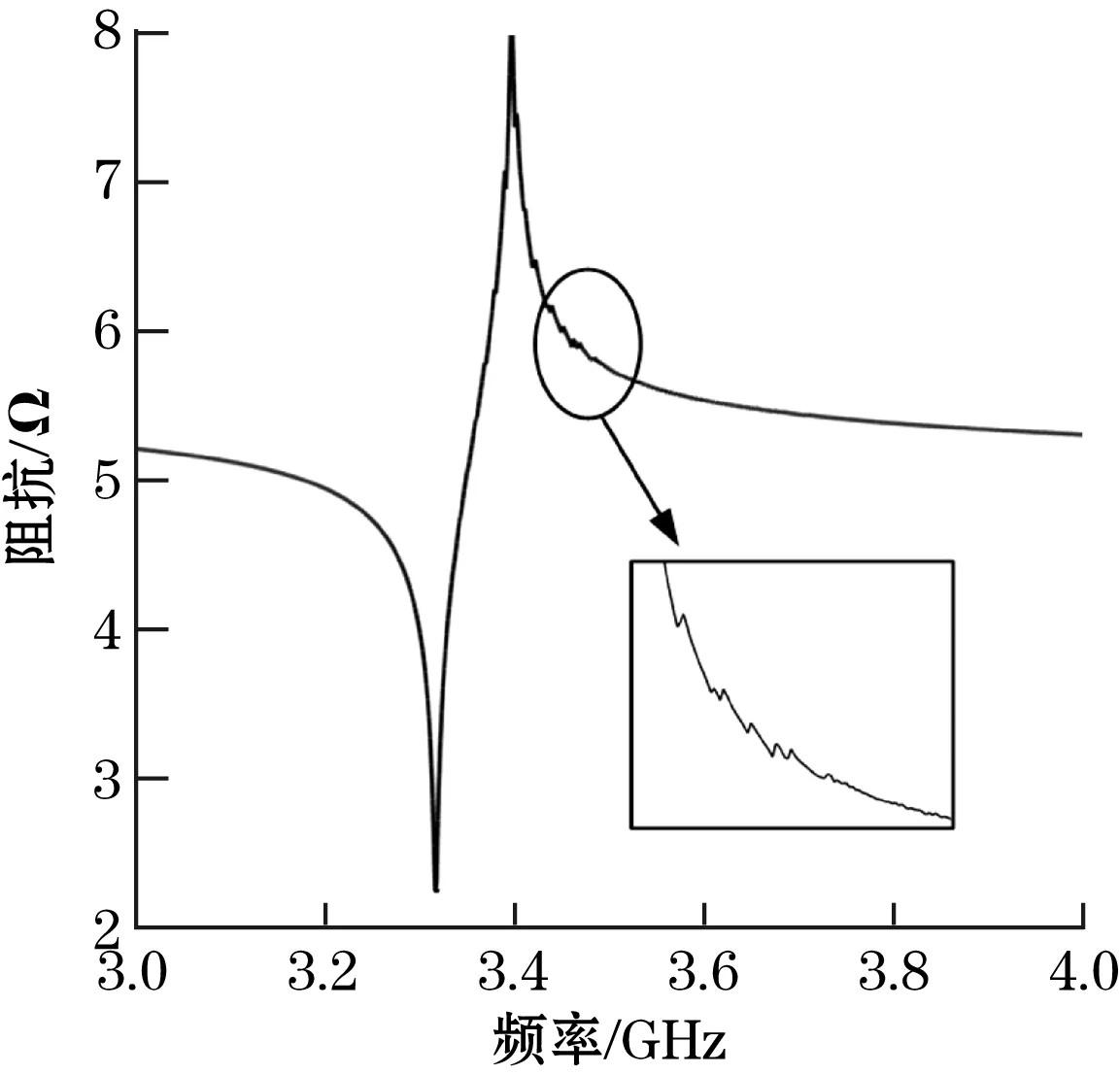
(a)3对

(b)4对

(c)5对
由图5可以看出,当布拉格反射栅对数为4的时候,BAW-SMR传感器的阻抗特性曲线最为光滑,此时传感器的串联谐振频率为3.258 GHz,并联谐振频率为3.392 GHz,由式(1)可知此时传感器的有效耦合系数为9.7%;当布拉格反射栅对数为3和5的时候,传感器的阻抗特性曲线出现寄生谐振。对具有寄生谐振的布拉格反射层,取具有3对布拉格反射栅的BAW-SMR传感器为例进行仿真分析,通过改变电极的尺寸来消除寄生谐振。上电极的尺寸和形状对体声波传感器的影响比下电极对传感器的性能影响大[9],所以主要通过改变上电极的尺寸来消除谐振。
首先改变电极尺寸(本次仿真的电极尺寸为400~800 nm,间隔为20 nm),发现当电极尺寸为720 nm的时候,阻抗特性的寄生谐振明显减少,曲线形状也没有很大改变,如图6所示,表明电极尺寸对寄生谐振有着一定的影响;然后改变电极厚度(本次仿真的电极厚度为10~80 nm,间隔为10 nm),通过仿真计算可以得到,当电极厚度改为0.02 μm时,寄生谐振几乎完全消除,此时的谐振频率为3.456 GHz,如图7所示,表明电极厚度对寄生谐振存在一定的影响,并且此时的谐振频率生改变,说明电极厚度对谐振频率也有一定的影响。

图6 3对布拉格反射栅通过改变电极尺寸得到的阻抗特性曲线

图7 3对布拉格反射层通过改变电极厚度得到的阻抗特性曲线
4 结束语
本文以ta-C为高声阻抗材料、AlN为低声阻抗材料构建布拉格反射栅结构,通过理论计算得到了BAW-SMR传感器的尺寸,利用COMSOL Multiphysics对具有不同布拉格反射栅对数的结构进行有限元仿真分析。首先,通过仿真分析得到该结构的导纳特性曲线和特性频率下的传感器的形变位移,形变位移在应变范围内,证明了传感器在该频率下的可行性;另外,通过对比不同反射栅对数条件下的阻抗特性曲线,可以看出在4对布拉格反射栅条件下传感器的阻抗特性曲线最为平滑,其他对数条件下传感器的阻抗特性曲线存在寄生谐振;最后,针对3对布拉格反射栅条件下阻抗特性曲线存在的寄生谐振峰进行优化,仿真了电极边长尺寸和厚度对寄生谐振的影响。

