基于结构输出响应的传感器故障检测研究

王 磊， 谭 平，程 涛， 周福霖

(1.安徽建工集团有限公司，安徽合肥 230031；2.广州大学工程抗震研究中心，广东广州 510405)

0 引言

在过去数十年中，随着大型复杂结构的大量涌现，为了保障重大结构在建造和运营过程中的安全性、完整性、适用性和耐久性，结构健康监测技术得到了广泛研究。其中基于环境激励的结构健康监测技术由于不需要外激励设备，也不会对结构产生额外的损伤，具有较好的经济性和实用性而被大量地研究和应用[1-8]。但是健康监测系统本身是一个复杂的系统，需要大量传感器提供结构响应数据，以保证系统的正常运行，因此传感器是结构健康系统的重要组成部分。然而在实际工程中，传感器装置由于自然损耗、环境改变和维护不及时等原因，难免会出现故障，甚至失效的情况。因此，在健康监测系统中对传感器进行实时的故障检测，从而确保传感器的正常工作，保障测量信号的可靠性，具有十分重要的理论和实际意义。早期对于传感器的故障，人们常以硬件冗余的方法确保系统安全工作。但硬件冗余法投资高，系统复杂性增加，工程不易实现。近年来基于动态冗余的传感器故障检测方法，因投资低、易于实现而受到了广泛研究。

基于动态冗余的传感器故障检测方法一般可以分为2类，即基于数据驱动方法和基于结构模型方法。其中，基于数据驱动方法需要收集大量的正常数据集进行分析，然后通过输出数据的统计特性检测故障的传感器[9]。所以数据集的大小和特性直接决定了基于数据驱动的故障检测方法的有效性。文献[10]通过对多个传感器量测信号相互关系的分析，识别出了故障信号及故障传感器。文献[11-12]通过基于历史测量数据构建的神经网络模型成功地检测并隔离了故障的传感器。相较于数据驱动方法，基于结构模型的故障检测方法充分利用了系统内部的信息来判别传感器故障，其具有在线计算量小、诊断迅速的优点，例如通过构建Kalman估计器或扩展Kalman估计器(extended Kalman estimator)生成残差，利用残差判别传感器的故障[13-15]。但是由于实际结构与构建的模型之间不可避免地存在一定的误差，因此，基于结构模型的方法很容易造成传感器故障的误判或漏判。

本文针对结构健康监测系统中恒偏差、变增益、缓慢漂移3种常见传感器故障，通过将前述两种传感器故障检测方法的优势相结合，提出了一种新型传感器故障检测方法。该方法首先通过已有量测数据利用随机子空间识别理论在线重构观测结构的离散状态模型，再直接利用识别出的离散状态模型构造多路Kalman估计器，并以此与实际传感器量测比较，产生输出残差，再通过比较输出残差绝对值，实现传感器故障的诊断和判别。其中对于基于结构模型的检测方法中存在的实际结构与模型的偏差及外环境的不确定性干扰，本文充分利用随机子空间识别方法识别时间短，所需数据较少的特点，通过每间隔一定的时间，依据最新量测数据在线更新结构模型和Kalman估计器，以确保所述检测方法的可靠性。最后通过一个数值模型和ASCE Benchmark 4层钢框架缩尺模型验证了本文所提方法的有效性和优越性。

1 随机子空间识别法

在环境激励下，n0层结构的离散状态空间模型为

(1)

式中：xk,yk分别为k时刻系统状态变量和观测变量,xk∈Rn，yk∈Rl；l为测量输出个数；n为系统阶数；A，C分别为系统的状态矩阵和系统输出矩阵；wk,vk分别为输入噪声和观测噪声ωk∈Rn,vk∈Rl。

假定噪声为零均值白噪声，满足

式中：E为数学期望；δ为Kronecker函数。

将响应测量输出y(k)组成2li×j的Hankel矩阵，并进一步将Hankel矩阵分成如下“过去”和“将来”2部分：

(2)

式中yi为i时刻所有量测响应。

(3)

(4)

式中( )+表示矩阵的广义逆。

(5)

对式(5)再进行奇异值分解(SVD)，则有

(6)

式中 ：W1，W2分别为左、右加权矩阵。通过不同加权矩阵的选取可产生不同的识别方式，比如BR法(Balanced Realization)，CAV法(Canonical Variate Analysis)等[7]，本文采用UPC算法(unweighted principal component algorithm)，W1，W2都取为单位矩阵；Un为n个主奇异值对应的左奇异值向量；Sn，Vn为相应的主奇异值和右奇异值向量。

(7)

式中Γi-1为矩阵Γi去除最后l行形成的矩阵。

求解线性方程组(1)可得到A，C的最小二乘解和白噪声序列如下式：

(8)

(9)

(10)

则由式(8)和式(10)所求参数A，C，Qi，Ri可以进一步构造Kalman估计器。随着采样的更新，本文利用最新量测数据替换旧有数据重复以上过程可实现对系统矩阵A，C及相应噪声矩阵Q，R的在线估计和更新，从而减小结构建模误差及外环境不确定性对于所述故障检测方法的影响。

2 Kalman估计器和传感器故障模型

2.1 Kalman估计器

由识别出的结构参数A、C可构造Kalman估计器如下：

(11)

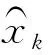
(12)

2.2 传感器故障模型

3 基于多路Kalman估计器的传感器故障检测

图1 传感器故障的多路检测策略

图2 多路Kalman估计器

其中，对于判决残差分布规律是否发生变化将由预设的传感器故障判决准则进行判断。为了更好地判别传感器故障，减少漏判和误判的发生，现对前述3种故障模型、实际环境振动与白噪声模型之间的差异对判决残差的影响进行分析。对于故障模型1、3，传感器恒定或缓慢漂移的存在都将使判决残差产生漂移；而对于故障模型2，传感器增益的衰减将直接导致判决残差的增大；在实际工程中，环境振动具有很强的不确定性，这将导致输出残差不完全满足预设的白噪声模型假定，因此，判决残差也具有一定的不确定性，不能仅通过超越阈值法来判别传感器故障。针对以上分析并结合一定的实践经验，本文提出如下2个传感器故障判决准则，以提高所述检测方法的准确性，避免误判、漏判：

(1)在1 s的时间间隔内，判决残差与阈值连续交差20次；

(2)判决残差以正斜率和负斜率与阈值交叉一次的时间间隔大于1 s；

其中，阈值的选取需在实际测量经验和传感器的噪声统计经验基础上经反复计算后才能大致确定，否则阈值取值过大，将对故障是否出现不敏感，容易造成漏报；反之，则会出现误报。

4 仿真分析

4.1 5层剪切型结构模型

某5层剪切型框架结构如图3所示，结构每层质量、刚度分别为m=125.53t，k=24.49×103kN/m，振型阻尼比为2%。结构每层设置一个加速度传感器，其标号如图3所示。考虑环境激励和传感器噪声分别是方差为1 m/s2和0.002 2 m/s2的有限白噪声(每层采样信号信噪比约为20)，加速度传感器采样频率为200 Hz。仿真时间为40 s，首先利用前15 s采样数据构造Kalman估计器，然后分别在22.5、30、37.5 s利用本时刻前15 s采样数据更新Kalman估计器。图4展示了随机子空间识别法在前15 s正常量测条件下对结构顶层加速度频响函数识别结果，可见随机子空间识别法能在短时间内识别结构特性。

图3 结构模型

图4 加速度频响函数

本例分以下3个工况进行仿真，每次仅考虑一个传感器在第16 s发生故障。工况1:5#传感器发生恒定漂移，漂移值为5#传感器无故障量测峰值绝对值的5%；工况2：5#传感器增益衰减为原增益的80%；工况3：5#传感器发生缓慢漂移，其中漂移值取α=0.01。针对此结构模型，本例将传感器反馈信号分解为5路信号，并针对每路信号设计了独立的Kalman估计器，以前述传感器故障判决方法判别传感器故障，其中故障阈值根据前15 s采样数据分析设为0.25。

相对前述3种工况，本文所述检测方法的检测结果分别如图5和表1所示。其中图5给出了第5路Kalman估计器的第5个判决残差，图中第一条竖向实线和第二条竖向实线分别是故障的出现时间和诊断时间，横向实线为设定的阈值线。从表1对于3种工况的检测结果可以看出基于Kalman估计器的多路故障检测方法能迅速准确地检测到故障的传感器，说明了本文提出的故障检测技术的正确性和可靠性。综合表1和图5可以发现所设计的Kalman估计器对于工况1、2中的故障模式诊断较为迅速；对于工况3，由于传感器缓慢偏移幅度较小，需要逐渐积累才能真正影响故障传感器的响应测量，故诊断时间较长。

图5 5#传感器判决残差

s

4.2 ASCE Benchmark结构模型

为进一步验证本文所述方法在实际环境振动下对于传感器故障的检测效果，现以ASCE Benchmark 4层钢框架缩尺模型(图6)最近一次环境振动试验数据(2002年8月)为例进行仿真。为了简化分析，本例仅采用布置在1～4层东、西两侧框架上的8个加速度传感器量测数据进行分析，其位置和编号分别如图7和表2所示，传感器采样频率为200 Hz，采样时间为300 s。关于该模型的详细信息及此次试验完整的试验数据、实验记录、设置工况等可登陆the ASCE Structural Health Monitoring Task Group's web page：https://nees.org/resources/1687查询。

图6 Benchmark钢框架缩尺模型

图7 传感器布置图

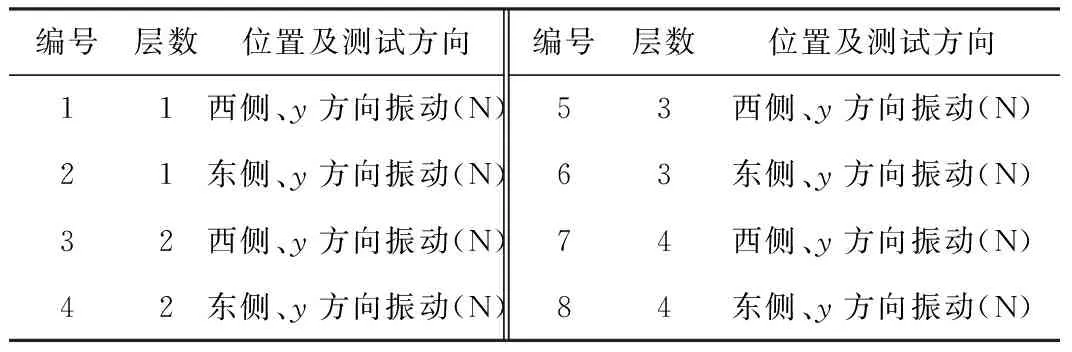
编号层数位置及测试方向编号层数位置及测试方向11西侧、y方向振动(N)53西侧、y方向振动(N)21东侧、y方向振动(N)63东侧、y方向振动(N)32西侧、y方向振动(N)74西侧、y方向振动(N)42东侧、y方向振动(N)84东侧、y方向振动(N)

图8为8个传感器记录数据的平均自功率谱密度曲线，可以看出结构的振动响应主要分布在0～30 Hz范围内，这是因为模型前五阶自振频率和外环境激励分布在此范围内[16]。因此，为了减少高频噪声的影响，提高识别结果的真实度，对前述传感器系统设计了一个8阶、通带截止频率为26 Hz的椭圆低通滤波器进行滤波。滤波前后2#传感器量测数据的自功率谱密度函数如图9所示，滤波后的自功率谱密度曲线在高频范围内迅速下降，但在结构响应区间内和原始数据保持了较好的相似性。

图8 自功率谱密度函数

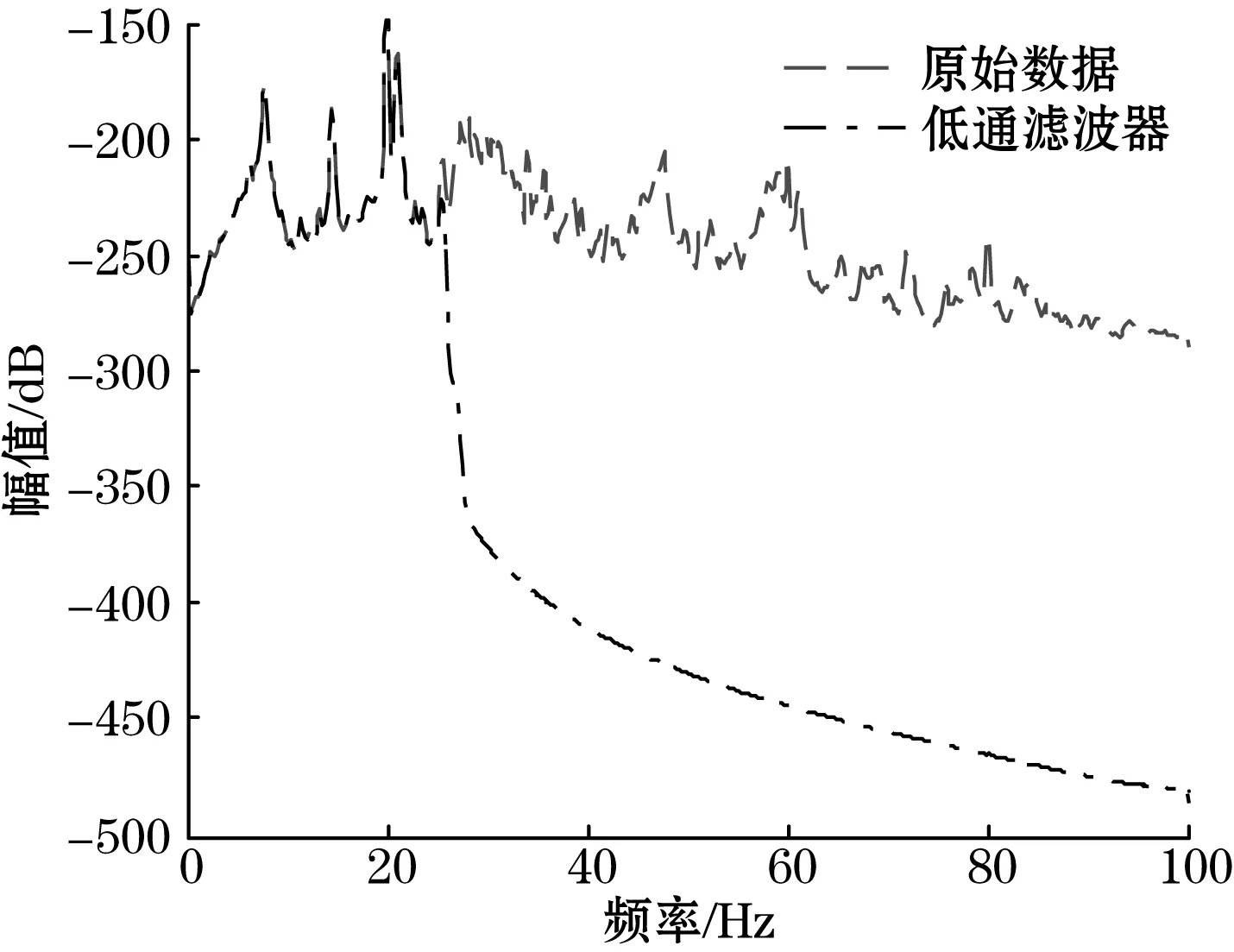
图9 2#传感器自功率谱密度函数

现对已滤波后的传感器量测数据进行仿真分析，采用前30 s采样数据构造Kalman估计器，然后每间隔30 s利用更新时刻前15 s采样数据更新Kalman估计器。假设8#传感器在50 s发生故障，对于加性误差故障模型取为8#传感器量测峰值的10%，对于传感器的增益改变取δ=0.8，传感器的缓慢漂移α=2×10-5。在本算例中继续采用前述传感器故障判决方法判决传感器故障，其中阈值向量定为15σ，σ如式(13)所示。在本例中，阈值已不再如前例所示为定值，而是随着最新的采样数据进行更新：

(13)

图10～图12展示了第8路Kalman估计器第8个判决残差，图中横向虚线、竖向实线和虚线分别代表了判决残差阈值、传感器故障开始时间和传感器故障判决时间。其中，对于故障模式1和2 ，所述的传感器故障检测方法大概花费1 s和0.695 s检测出传感器故障；对于故障模式3，与前述模型相同，由于传感器缓慢偏移幅度较小，需要逐渐积累才能影响传感器量测值，故诊断时间较长，需要11.71 s。

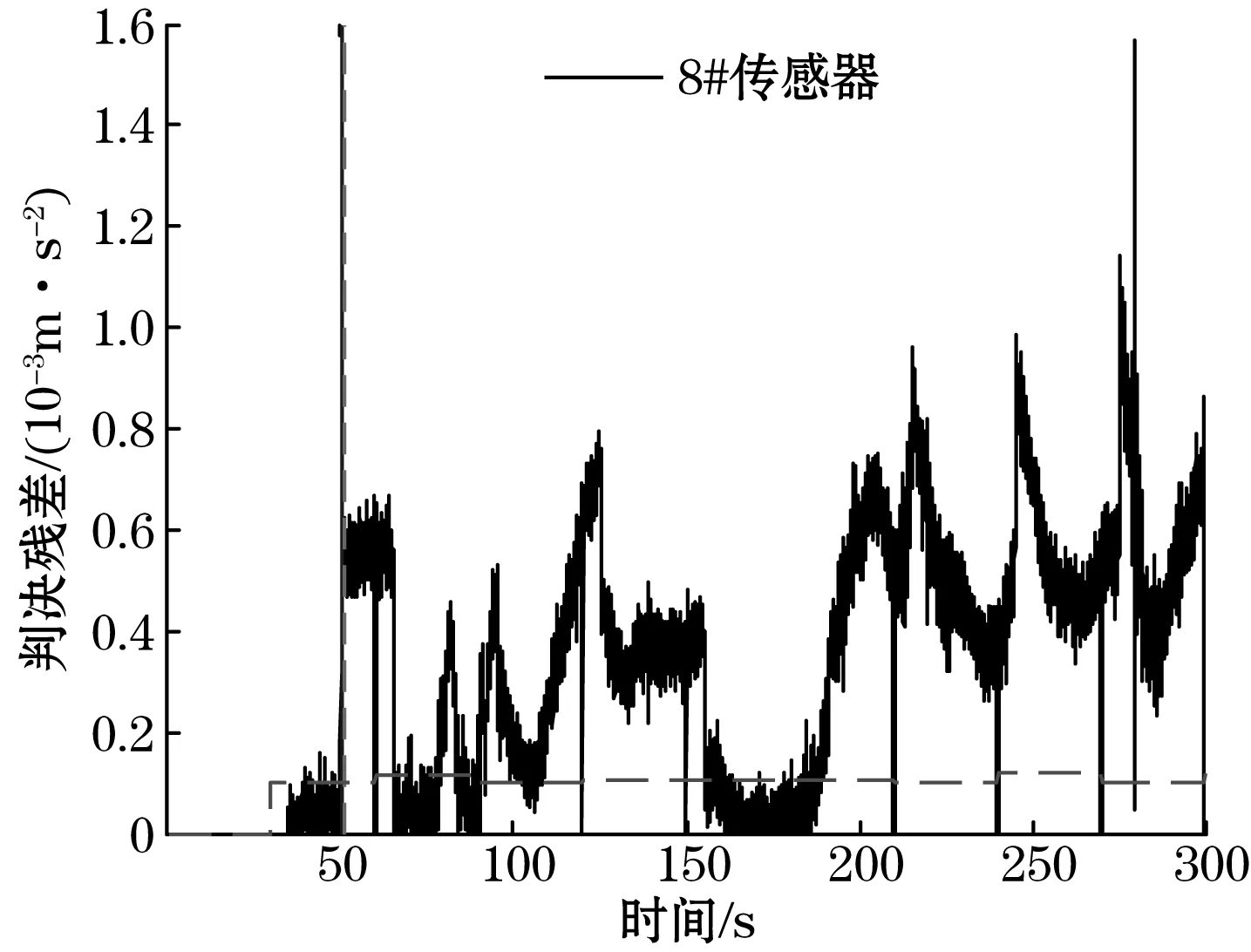
图10 故障模式1判决残差

图11 故障模式2判决残差

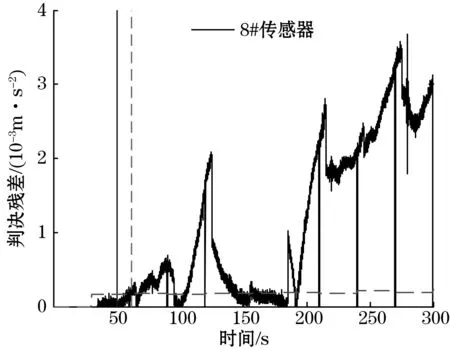
图12 故障模式3判决残差

5 结论

本文提出一种基于随机子空间法和Kalman估计器，利用输出残差实现的传感器故障检测方法，并在文末通过某5层剪切型结构和ASCE Benchmark 4层钢框架缩尺模型，验证了所述方法的有效性和适用性，得到以下一些主要结论：

(1)在结构健康监测系统中，对于3种常见的传感器故障模式，可以采用本文所述多路检测方法通过合理的设计和配置Kalman估计器，利用输出残差，快速地诊断传感器故障；

(2)通过传感器对于结构在环境激励下振动响应的量测结果，随机子空间法可以较好地识别结构特性，建立结构的离散空间模型；利用已识别的离散空间模型构造的Kalman估计器可较准确地估计下一时刻结构输出响应；

(3)本文所述传感器故障检测方法对于传感器的加性误差和增益改变诊断较为迅速；对于传感器的缓慢漂移，当其偏移幅度较小时，需要逐渐积累才能真正影响故障传感器的量测值，故诊断时间相对较长。