Some Topological Indices Computing Results If Archimedean Lattices L(4,6,12)
Kang Qiong and Xinting Li
Abstract: The introduction of graph-theoretical structure descriptors represents an important step forward in the research of predictive models in chemistry and falls within the lines of the increasing use of mathematical and computational methods in contemporary chemistry. The basis for these models is the study of the quantitative structure-property and structure-activity relationship. In this paper, we investigate Great rhom-bitrihexagonal which is a kind of dodecagon honeycomb net-work covered by quadrangle and hexagon. Many topological indexes of Great rhom-bitrihexagonal have being investigated, such as sum-connectivity index, atom-bond connectivity index,geometric-arithmetic index, fifth, harmonic index, Randić connectivity index, first Zagreb index, second Zagreb index and the corresponding Zagreb polynomials, modified Zagreb index, fourth atom-bond connectivity index, augmented Zagreb index, hyper-Zagreb index, Sankruti index, forgotten topological index, first multiple Zagreb index,second multiple Zagreb index, as well as derived geometric-arithmetic index, Narumi-Katayama index and modified Narumi-Katayama index.
Keywords: Topological index, L4,6,12 circumference, graph theory, molecular biology.
1 Introduction
There is an undirected graph without multiple edges and loops that is considered in this paper. We defineGas a graph, and defineE(G)andV(G)as the edge set and vertex set of G. In additional, we defined(v)as the degree of the a vertexvandN(v)as the set of neighbours ofvin graph. We useEa,bexpress the set of edges that the degrees of end verticesaandb, i.e.Ea,b={uv| {a,b}={d(u),d(v)}. Let the summation of a vertexubesG(u), i.e.sG(u)=and E'a,b={uv|{a,b}={sG(u),sG(v)}}. Topological Index has been derived for many years, the theory of chemical graph contains both compute graph theory and chemical graph theory. As a newly boundary science between chemistry and computer science, which become more and more concerned [Luo and Zhang (2012)]. It has become a significant branch of mathematical chemistry. In traditional chemistry, the researchers exploit the chemical properties of matter by means of experiment. But in molecular chemistry, a molecular structure is viewed as a so-called chemical graph, in which way, vertices is regarded as chemical atom and edge is regarded as chemical bond.As a useful tool of research, chemical graph is applied to reveal the relationships between various physical characteristics and chemical structures, such as biological activity,chemical reactivity [Van, Carter, Grassy et al. (1997)]. In 1947, Harold Wiener first used topological indices on the research of paraffin's boiling points. In his paper, Wiener index is introduced to reveal relationships between the index of their molecular graphs and physicochemical properties of organic compounds [Iranmanesh, Alizadeh and Taherkhani(2008)]. Furthermore, such an index reveals the correlations of physicochemical properties of alkanes, alcohols, amines and their analogous compounds [Ali, Yaser and Bahman(2008)]. There was Randić connectivity index, one of topological indexes, applied to the study of branching properties of alkanes [Randic (1975)].
Definition 1The connectivity index (or Randić Index) of a graph G, denoted by χ(G),was defined as follow:

There is another Randić index, named the harmonic index, as is first introduced in Fajtlowicz et al. [Fajtlowicz and Waller (1986)].
Definition 2The harmonic index H(G) is defined in a graph as follow.

In 1998, Estrada et al. [Estrada, Torres and Rodríguez et al. (1998)] put forward the atombond connectivity (ABC) index, in order to improve Randić classic connectivity index.
Definition 3Estrada introduced ABC index, also named atom-bond connectivity index,in 1998. And ABC index is defined as

In 1998, Estrada [Estrada (2008)] demonstrated that there is a linear relationship between alkanes’ experimental heats of formation and ABC index. Furthermore, in 2008, Estrada built the physical basis for this relationship. A new version of ABC index was introduced by Ghorbani et al. [Ghorbani and Hosseinzadeh (2010)], named (ABC4) index.
Definition 4The new version of atom-bond connectivity(ABC4)index is defined as

In 2010, Furtula et al. [Furtula and Gutman (2015)] refers a new topological index,named “augmented Zagreb index”, and furthermore, the upper and lower bounds of chemical tree can be attained.
Definition 5The augmented Zagreb index AZI(G) is defined as

In 1972, Gutman et al. [Gutman and Trinajstić (1972)] introduced the first and second Zagreb indiecs of a molecular graph.
Definition 6The first Zagreb index M1(G)[Nikolić, Kovačević, Miličević et al. (2003)] is defined as
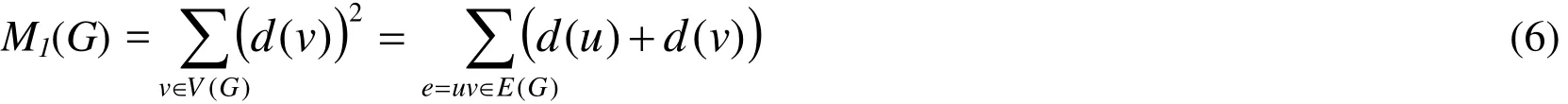
Definition 7The second Zagreb index M2(G)[Nikolić, Kovačević, Miličević et al. (2003)]is defined as

In 1972, Furtula et al. [Furtula and Gutmanstudied the total π-electron energy’s structure-dependency. He found that there was a relationship between the sum of square of the vertex degrees of the molecular graph and the total π-electron energy’s structuredependency. At the same time, he introduced the “forgotten topological index”.
Definition 8The forgotten topological index F(G) defined by Furtula is shown as follow:

On the basis of the above Zagreb indices, the first Zagreb polynomialM1(G,x) and the second Zagreb polynomialM2(G,x) have been defined [Farahani (2013); Fath-Tabar(2009)].
Definition 9The first Zagreb multinomial M1(G,x)is defined as

Definition 10The second Zagreb multinomial M2(G,x) is defined as

A problem with the Zagreb indices is that their contributing parts give greater weights to inner vertices and edges and smaller weights to outer vertices and edges of a graph. This opposes intuitive reasoning that outer atoms and bonds should have greater weights than inner vertices and bonds because outer vertices and bonds are associated with a larger part of the molecular surface and are consequently expected to make a greater contribution to physical, chemical and biological properties [Miličević and Nikolić(2004)].So the modified Zagreb index was proposed to correct the problem that former Zagreb(G) index contributing more weights to inner bonds and less weights to outer bonds. According to chemists' intuition, this index, on the contrary, outer bonds should have greater weights than inner bonds.
Definition11The modified Zagreb index M(G) is defined as

Zhou et al. [Zhou and Trinajstić (2009)] presents a novel connectivity index for molecular graphs, named sum-connectivity index, gives lower and upper bounds when graph structural invariant.
Definition12The sum-connectivity index is defined [Zhou and Trinajstić (2009)] as

Vukičević proposed a new topological index based on the end-vertex degrees of edges named as geometrical-arithmetic index (GA), and presented its basic features.
Definition13The expression of geometric-arithmetic index is defined as

Graovac et al. [Graovac, Ghorbani and Hosseinzadeh (2011)] lately introdue the fifth geometric-arithmetic topological index.
Definition14The fifth geometric-arithmetic topological index GA5 is defined as

In 2013, Shirdel et al. [Shirdel, Rezapour and Sayadi (2013)] defined a new distancebased Zagreb indice named “hyper-zagreb index”.
Definition15The hyper-Zagreb index is defined as

Based on the many researches recently, Hosamani [Hosamani (2017)] proposed a new topological index, named “Sanskruti index S(G)” of a molecular graph G that can be utilized to estimate the bioactivity of chemical compounds.
Definition16The Sankruti index of a graph G is defined as

Based on degrees of vertices in a given molecular graph, Ghorbani et al. [Ghorbani and Azimi (2012)] produced the multiple versions of Zagreb indices. They are named as the first multiple Zagreb index and the second multiple Zagreb index.
Definition17The first multiple Zagreb index PM1(G)is defined as:

Definition18The second multiple Zagreb index PM2(G)is defined as:

In 1984, Narumi et al. [Narumi and Katayama (1984)] defined “simple topological index”as the product of orders at vertexes of a graph. It can be used on the study of thermodynamic data including boiling points. Recently, more studies on the graph widely introduced “Narumi Katayama index” [Tomovic and Gutman (2001)].
Definition19Narumi et al. [Narumi and Katayama(1984)] defined this index as follow:

Definition20Ghorbani et al. [Ghorbani and Azimi (2012)] defined the modified Narumi-Katayama index, in which each vertex degree d is multiplied d times.

It can be seen in this paper, the modified Narumi-Katayama index and second multiplicative Zagreb index are the same.
2 Results
The Archimedean lattices are the graphs of vertex transitive, it can be embedded in a plane that each face is a regular polygon [Martinez (1973)].The family of Archimedean lattices contains 11 kinds of 2D lattices, which include the famous honeycomb lattices and square, triangle, kagomé. Based on the sizes of faces incident to a given vertex, the names of the lattices are given. The sizes of face are listed in order, from the smallest to largest. So, in this way, we can nominate the Archimedean lattices as follow (4, 4, 4, 4),abbreviated to (44), Kagome is (3, 6, 3, 6) [Codello (2010)] and honeycomb is called (63).In this paper, we define an archimedean lattice called (4, 6, 12). And we name this lattice L4,6,12circumference. In geometry, the Great rhombitrihexagonal contains one dodecagon,two hexagons, and three squares on each edge, as is shown in Fig. L4,6,12(n) and in Fig.L4,6,12(n) molecular structure wheren=2 circle is shown. Furthermore Fig. L4,6,12(n)presents then=3 circle.

Figure 1: The Archimedean lattice L4,6,12(n)
In terms of observing and computing, we can induce the |V2|=6n, |V3|=18n2-6n. And by means of further calculating, we can inferE(s,t)andS(s,t)corresponding to differents,andt, as is shown in the Tab. 1.

Table 1: Partition the edge set of L4,6,12(n) into Es,t

Table 2: Partition the edge set of L4,6,12(n) into E’s,t
Theorem 1Let G be and L4,6,12(n) circumference, then
ProofThe result is obtained based on the edge partition given in Tab. 1.By the definition of ABC4index, we have
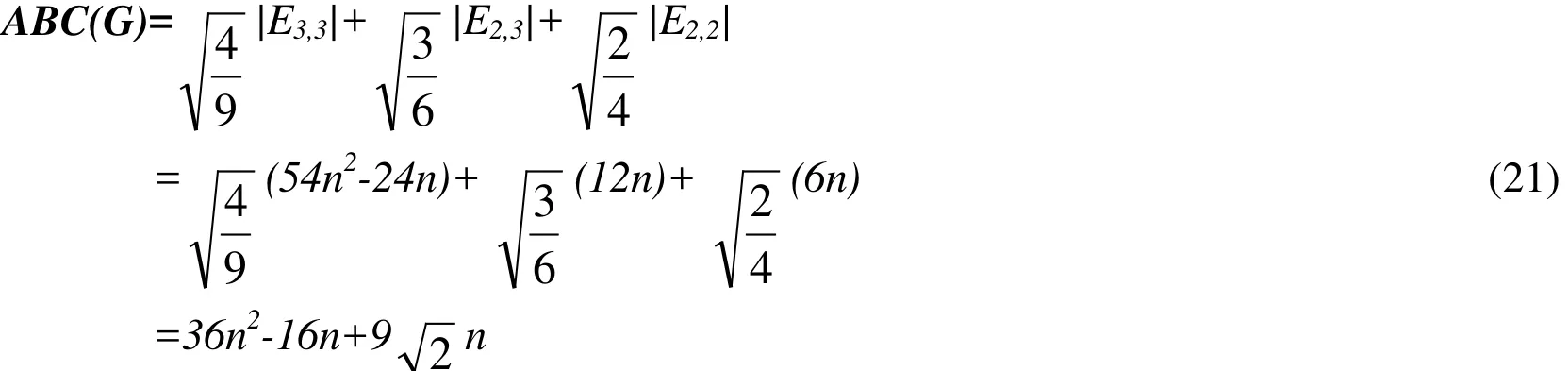
Theorem 2Let G be an L4,6,12(n) circumference, then
ProofThe result is obtained based on the edge partition given in Tab. 2.By the definition of Atom-bond Connectivity index, we have

Theorem 3Let G be an L4,6,12(n) circumference, then
ProofBased on the edge partition given in Tab. 2. The result of equation can be obtained.By the definition of Randić connectivity index, we have
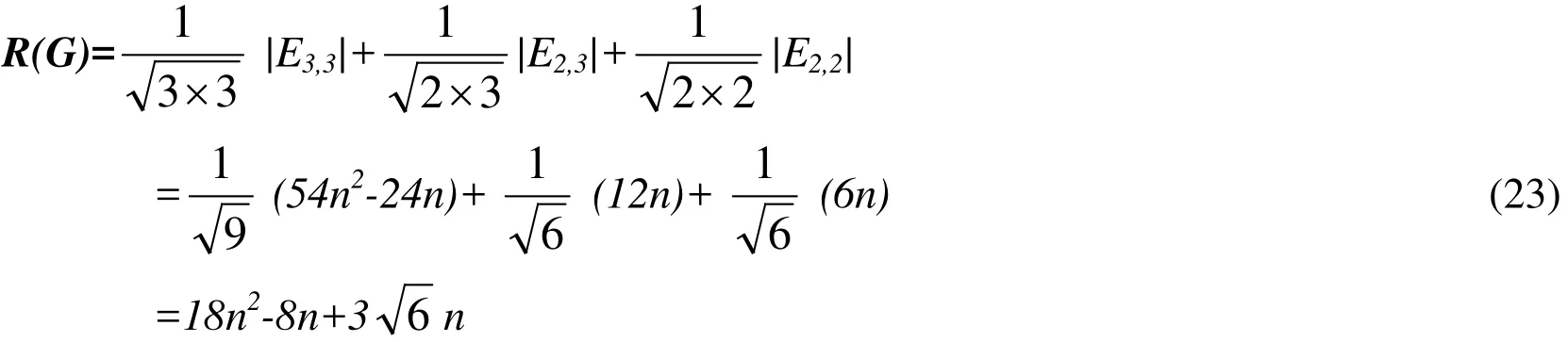
Theorem 4Let G be an L4,6,12(n) circumference, then Χ(G)=
ProofThe result is obtained based on the edge partition given in Tab. 2. According to the definition of sum-connectivity index, we have
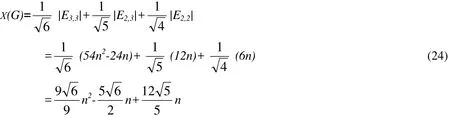
Theorem 5Let G be an L4,6,12(n) circumference, then M1(G)= 32n2-60n.
ProofThe result is obtained based on the edge partition given in Tab. 2. By the definition of First Zagreb index, we have

Theorem 6Let G be an L4,6,12(n) circumference, then M2G)=486n2-120n.
ProofThe result is obtained based on the edge partition given in Tab. 2. By the definition of Second Zagreb index, we have

Theorem 7Let G be an L4,6,12(n) circumference, then M1(G,x)=(54n2-24n)x6+12nx5+6nx4
ProofThe result is obtained based on the edge partition given in Tab. 2. By the definition of First Zagreb polynomialM1(G,x)index, we have
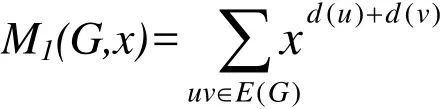

Theorem 8Let G be an L4,6,12(n) circumference, then M2(G,x)=(54n2-24n)x9+12nx6+6nx4
ProofThe result is obtained based on the edge partition given in Tab. 2. By the definition of Second Zagreb polynomialM2(G,x)index, we have

Theorem 9Let G be an L4,6,12(n) circumference, then
ProofThe result is obtained based on the edge partition given in Tab. 2. By the definition of Augmented Zagreb index, we have
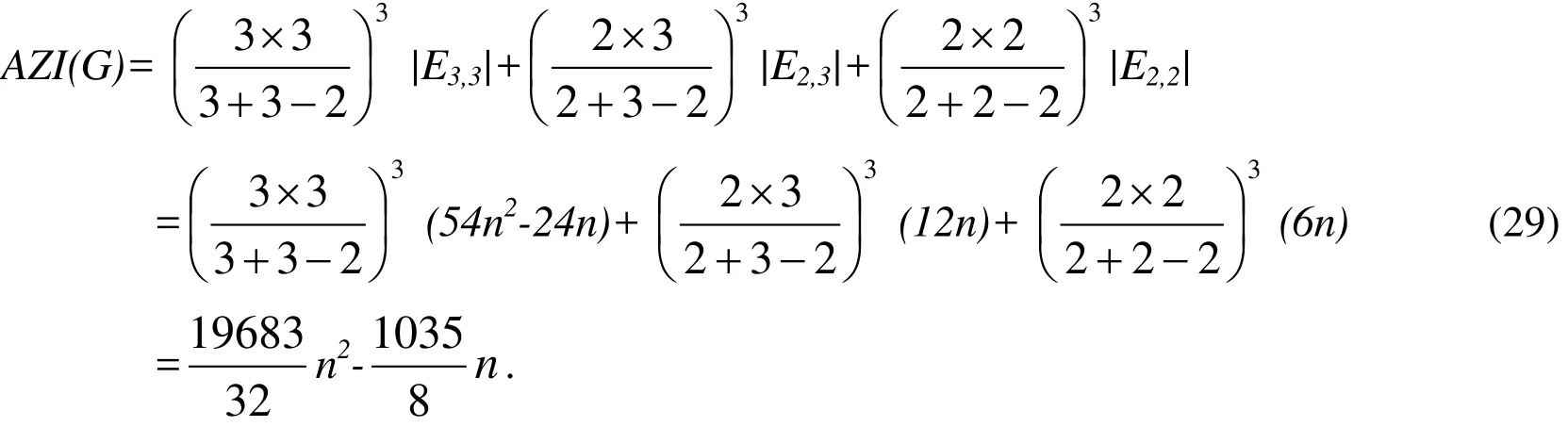
Theorem 10Let G be an L4,6,12(n) circumference, then
ProofThe result is obtained based on the edge partition given in Tab. 2. By the definition of modified Zagreb index, we have
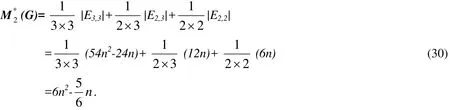
Theorem 11Let G be an L4,6,12(n) circumference, then HM(G)=1944 n2-468n
ProofThe result is obtained based on the edge partition given in Tab. 2. By the definition of hyper-Zagreb index, we have
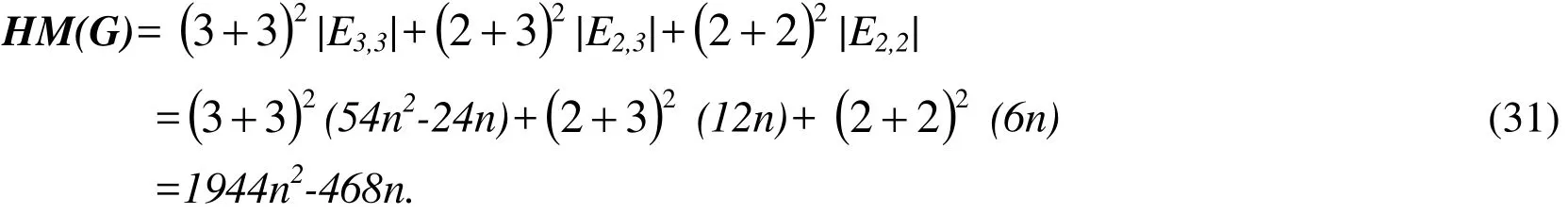
Theorem 12Let G be an L4,6,12(n) circumference, then
ProofThe result is obtained based on the edge partition given in Tab. 2. By the definition of Geometric-Arithmetic index, we have

Theorem 13Let G be an L4,6,12(n) circumference, then GA5(G)=54n2+
ProofThe result is obtained based on the edge partition given in Tab. 2. By the definition of GA5index, we have

Theorem 14Let G be an L4,6,12(n) circumference, then S(G)=(54n-48n+6)2-
ProofThe result is obtained based on the edge partition given in Tab. 2. By the definition of Sankruti index, we have

Theorem 15Let G be an L4,6,12(n) circumference, then F(G)=972n2-228n.
ProofThe result is obtained based on the edge partition given in Tab. 2. By the definition of forgotten index, we have
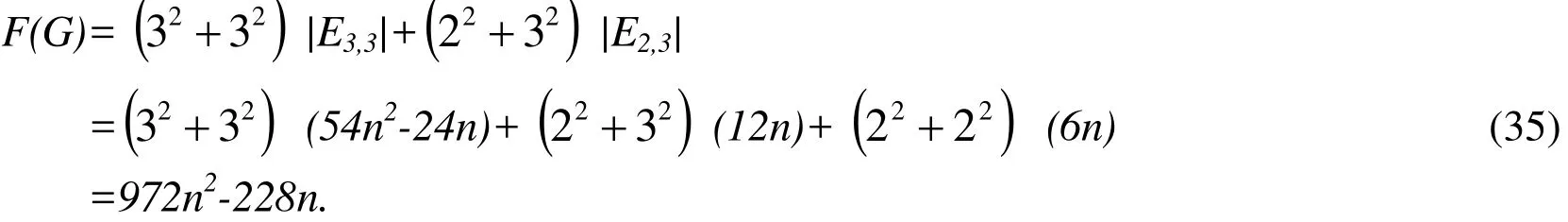
Theorem 16Let G be an L4,6,12(n) circumference, then H(G)=18n2-
ProofThe result is obtained based on the edge partition given in Tab. 2. By the definition of Harmonic index, we have
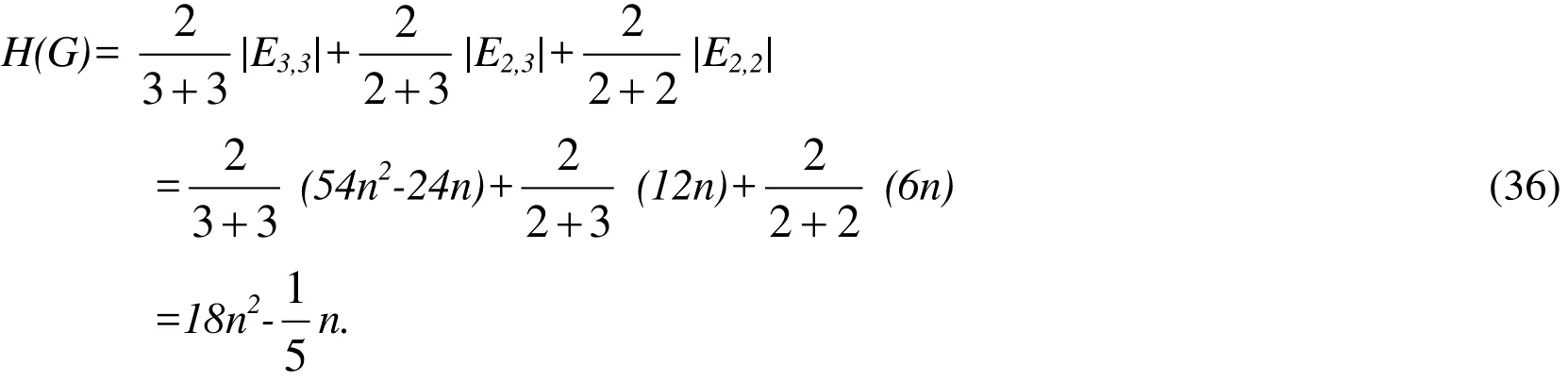
Theorem 17Let G be an L4,6,12(n) circumference, then
ProofThe result is obtained based on the edge partition given in Tab. 2. By the definition of first multiple Zagreb index, we have

Theorem 18Let G be an L4,6,12(n) circumference, then
ProofThe result is obtained based on the edge partition given in Tab. 2. By the definition of first multiple Zagreb index, we have

Theorem 19Let G be an L4,6,12(n) circumference, then
ProofThe result is obtained based on the edge partition given in Tab. 2. By the definition of second multiple Zagreb index, we have

Theorem 20Let G be an L4,6,12(n) circumference, then
ProofThe result is obtained based on the edge partition given in Tab. 2. By the definition of modified Narumi-Katayama index, we have

3 Conclusions
The topological index is defined for a topological graph which has nothing to do with distances, angles, steric strain, or hindrance. Therefore, without substantial modification,the topological index cannot account for the difference in physical quantities of geometrical isomers, or for the overcrowded effect expected for compounds having vicinal quarter carbon atoms. So these indexes are expected to be dependent on the topological nature of the skeleton of a system like a molecule.
A class of dodecagon honeycomb network which is covered by C4, C8and C12has been investigated here, and formulas for their Randić connectivity index, fourth Atom-Bond Connectivity index, Geometric-Arithmetic index, fifth Geometric-Arithmetic index,Atom-Bond Connectivity index, First Zagreb index, Second Zagreb index and the corresponding Zagreb polynomials, modified Zagreb index, Augmented Zagreb index,hyper-Zagreb index, forgotten topological index, first multiple Zagreb index, second multiple Zagreb, harmonic index, Sankruti index, index, Narumi-Katayama index and modified Narumi-Katayama index have been derived.
 Computers Materials&Continua2019年1期
Computers Materials&Continua2019年1期
- Computers Materials&Continua的其它文章
- Development and Application of Big Data Platform for Garlic Industry Chain
- ia-PNCC: Noise Processing Method for Underwater Target Recognition Convolutional Neural Network
- Spatial Quantitative Analysis of Garlic Price Data Based on ArcGIS Technology
- Estimating the Number of Posts in Sina Weibo
- GA-BP Air Quality Evaluation Method Based on Fuzzy Theory
- A Robust Image Watermarking Scheme Using Z-Transform,Discrete Wavelet Transform and Bidiagonal Singular Value Decomposition
