A Robust Image Watermarking Scheme Using Z-Transform,Discrete Wavelet Transform and Bidiagonal Singular Value Decomposition

N.JayashreeandR.S.Bhuvaneswaran

Abstract: Watermarking is a widely used solution to the problems of authentication and copyright protection of digital media especially for images, videos, and audio data. Chaos is one of the emerging techniques adopted in image watermarking schemes due to its intrinsic cryptographic properties. This paper proposes a new chaotic hybrid watermarking method combining Discrete Wavelet Transform (DWT), Z-transform (ZT)and Bidiagonal Singular Value Decomposition (BSVD). The original image is decomposed into 3-level DWT, and then, ZT is applied on the HH3 and HL3 sub-bands.The watermark image is encrypted using Arnold Cat Map. BSVD for the watermark and transformed original image were computed, and the watermark was embedded by modifying singular values of the host image with the singular values of the watermark image. Robustness of the proposed scheme was examined using standard test images and assessed against common signal processing and geometric attacks. Experiments indicated that the proposed method is transparent and highly robust.

Keywords: Digital watermarking, chaotic mapping, z-transform, arnold cat map, discrete wavelet transform (DWT), bidiagonal singular value decomposition (BSVD).

1 Introduction

Increased usage of the internet and the availability of high-speed digital data networks made online transmission and distribution of multimedia contents over the web to grow exponentially. Copyright protection and authentication of these data are of primary concern since it can be duplicated, modified and re-transmitted easily. Digital watermarking is not only a solution to address security concerns of digital media but also facilitates copyright protection and authentication. It is also an important branch of information hiding, as it can be applied to high strength secure communication. A watermark is a sequence, carrying information, embedded into a digital image [Cox,Kilian, Leighton et al. (1997)]. It provides an excellent method for copyright protection of multimedia by embedding copyright information in them.

Watermarking algorithms can be broadly classified into two categories based on the embedding process; one is spatial domain and second is frequency domain schemes. The spatial domain method directly alters the pixel values of the original image to embed the watermark. Although algorithms in this category are simple to implement, sophisticated operations require more computing resources and time. This drawback makes schemes in this category unsuitable for real-time situations. Transform domain schemes were proposed to overcome the limitations of the spatial domain method. The transform domain schemes, in the process, convert the original data, which is in the spatial domain,into a transform domain and vice versa. These conversions are made by utilizing mathematical transformation such as Discrete Fourier Transform (DFT), Discrete Cosine Transform (DCT), Z-transform (ZT) and Discrete Wavelet Transform (DWT). DWT is most commonly used in frequency domain watermarking due to its excellent spatiotemporal characteristics. Imperceptibility and robustness are two significant characteristics used to evaluate watermarking schemes. In order to improve robustness and imperceptibility, many hybrid watermarking schemes have been proposed combining various mathematical transformation.

A hybrid watermarking technique developed by Lai et al. [Lai and Tsai (2010)]employing single-level Haar DWT and SVD. In this scheme, the watermark image is divided into two parts and embedded into two different sub-bands to improve robustness and imperceptibility.

The image watermarking algorithm combining DWT, DCT, and SVD proposed by Fazli et al. [Fazli and Moeini (2016)] seeks to achieve robustness against geometric attacks. In this scheme, the host image is divided into four non-overlapping sub-images and the watermark is embedded in each sub-image independently. The semi-blind image watermarking scheme proposed by Saxena et al. [Saxena, Saxena and Rastogi (2014)],using trigonometric functions is robust against geometric distortions. The scheme is based on DWT, DCT, and SVD.

Bhatnagar et al. [Bhatnagar and Raman (2009)] introduced a robust semi-blind reference watermarking scheme based on DWT and SVD. In their another scheme [Bhatnagar, Wu and Raman (2012)] combining fractional wavelet packet transform, quadratic residues and SVD, the watermark strength for each embedding location is chosen from two candidate strengths using quadratic residue properties.

Shi [Shi (2014)] presented a robust scheme using DWT and SVD with circulation. In this scheme, Chebyshev map is used for scrambling the watermark information. In the hybrid image watermarking scheme based on DCT [Sverdlov, Dexter and Eskicioglu (2005)],the coefficients are mapped into four quadrants using the zig-zag sequence and show that watermark embedded in lower frequencies are robust against a set of attacks while watermark embedded in higher frequencies withstand against a different set of attacks.

Although, SVD is a widely used technique in the design of robust watermarking algorithms, the issue of the false positive problem (FPP) is a severe drawback. [Ling,Phan and Heng (2013); Makbol, Khoo and Rassem (2018); Xing and Tan (2010)]. Many FPP resistant SVD-based schemes have been proposed.

Ansari et al. [Ansari, Pant and Ahn (2016)] proposed a solution to the FPP in their method by embedding a signature generated using the UV matrices it in the HH sub-band of the host image. This signature is authenticated during the extraction process.

A block-based DWT-SVD watermarking scheme developed by Makbol et al. [Makbol, Khoo and Rassem (2016)] employed human visual system (HVS) characteristics for block selection and embedded a binary watermark in the U matrix to overcome the false positive problem.

Z-transform has been widely used for several image processing applications such as authentication, copyright protection and tamper detection [Ho, Zhu and Shen (2004); Ho,Zhu, Shen et al. (2008); Khan, Boda and Bhukya (2012); Mandal (2012); Rabiner,Schafer and Rader (1969); Stillings (1972); Takaya, Shimizu, Kitama et al. (1990); Vich(1987)]. The locations of the zeros of the z-transform are highly sensitive to changes in the pixel value, which is suitable for fragile watermarking. It is also easy to implement and provides better data hiding property. Based on these properties of Z-transform, Ho et al. [Ho, Zhu, Shen et al. (2008)] proposed a fragile watermarking scheme by encoding the zeros of the Z-transform. Ho et al. [Ho, Zhu and Shen (2004)] proposed another scheme for authentication of biomedical images based on zero location watermarking. Z-transform is also used in image steganography for grayscale images [Mandal (2012)]. A Z-transform-DWT based scheme was proposed by Jayashree and Bhuavaneswaran[Jayashree and Bhuvaneswaran (2016)].

In this paper, a watermarking algorithm using Z-transform, DWT, and BSVD is proposed.Arnold cat map is used to encrypt the watermark image to improve the security of the scheme. The rest of the paper is organized as follows: The Next part of the paper is Section 2 where, the Arnold Cat map, DWT, Z-transform, and BSVD are explained. In Section 3, the proposed algorithm is discussed in detail. Experimental results and performance analysis are presented in Section 4 before concluding the paper in Section 5.

2 Preliminaries

2.1 Discrete wavelet transform

Wavelet is a powerful mathematical tool used in a wide variety of applications like image denoising, data compression, watermarking and fingerprint verification [Sifuzzaman,Islam and Ali (2009)]. It provides a better representation of data by using Multi-Resolution Analysis (MRA). When DWT is applied to an input signal, it is decomposed into four sub-bands namely LL (low frequency), HH (high-frequency), HL (horizontal level frequency) and LH (vertical level frequency) sub-bands. The LL sub-band can be further decomposed into similar four sub-bands. Similarly, the input signal can be decomposed up to n-levels. DWT has both spatial and frequency information simultaneously thus provides the spatiotemporal representation of the data. It is also considered that the DWT represents the characteristics of the human visual system efficiently than other transform methods. The advantages of using wavelet transform include (1) simultaneous localization of data both in time and frequency domain and, (2)finer approximation of the data with few coefficients of the wavelets.

2.2 Z-transform

The z-transform plays a pivotal role in processing discrete data [Ho, Zhu, Shen et. al.(2008)]. Z-transform is a suitable and valuable tool for representing, analyzing and designing discrete-time signals and systems [Ho, Zhu, Shen et al. (2008)].

The z-transform of a discrete time signal x[n] is defined as

where, z is a complex variable. In the case of a sequence of image pixels, x(n) may be nonzero only in the interval 0≤n≤∞, and the Eq. (3) reduces to one-sided z-transform.

The inverse Z-transform is used to recover the discrete time sequence, x(n), given its Z-transform. Symbolically, the inverse Z-transform may be defined as

where X(z) is the Z-transform and Z-1is the function for the inverse Z-transform. An algorithm for numerically calculating the Z-transform of a sequence of N samples is proposed by Rabiner et al. [Rabiner, Schafer and Rader (1969)]. This algorithm is termed as chirp Z-transform (CZT), and it is used to compute the Z-transform effectively at points in z-plane which lie on a spiral or circular contour at any arbitrary point.Application of this algorithm in digital watermarking improves the robustness and imperceptibility of the watermarked image. It is also best suited for many other image processing applications such as filtering, interpolation, and correlation.

There are many potential applications wherein the CZT algorithm is used like spectral analysis of speech, to the individual periods of voice with great success [Ho, Zhu and Shen (2004)]. The ability to evaluate the Z-transform inside and outside the unit circle and to efficiently analyze high resolution, narrow frequency spectrum bands help watermarking algorithms to improve robustness and imperceptibility of the watermarked image.

2.3 BSVD

The decomposition of a matrix into the orthogonal matrix and the diagonal matrix is termed as singular value decomposition. It is given by the formula

where, S is the singular value matrix, and U and V are orthogonal matrices, generally termed as left and right singular matrices respectively.

The properties of the singular value decomposition are (1) the singular values of the image matrix remain less altered when it is subjected to various attacks (2) also, the singular values of the image matrix depict intrinsic algebraic characteristics which shows that SVD can be used in image processing methods.

The spectral decomposition based on SVD can be considered as bidiagonal SVD. The singular values obtained using BSVD are similar to SVD, although the method of calculating BSVD and SVD are different. The BSVD is calculated by bidiagonalizing A,and subsequently taking SVD on the upper bidiagonal values, as shown below:

where, A is an orthonormal matrix, PAand QAare unitary matrices and B is the upper bidiagonal matrix.

where, PBand QBare unitary matrices and S is the singular values of the matrix.

The calculation of SVD, which uses iterative schemes to calculate the singular values,differs from that of BSVD, where it uses finite operations. The performance of BSVD is better than SVD [Deift, Demmel and Tomei (1991)].

2.4 Arnold cat map

Arnold Cat Map (ACM), named after Vladimir Arnold, is a chaotic map. Arnold’s cat map is the transformation

given by the formula

where x, y∈{0,1,2 …,n-1} and n is the size of the image.

When the image is encrypted using Arnold cat map, the original image is obtained back,after N number of times, and N is called the period of the function [Chen, Wong, Liao et al.(2013)].

3 Proposed scheme

3.1 Watermark embedding

Let the cover image of size M×N be denoted byIand the grayscale watermark logo image of size M1×N1be represented byW, the steps for embedding the watermark are given below:

1. The watermark image W, scrambled and encrypted using the Arnold transformation is divided into two parts: W1and W2.

2. Applyn-level discrete wavelet transform on the cover imageIto obtain the following four sub-bands LLn, LHn, HLn, HHn. Of these, HLnand HHnare considered for embedding the watermark. In the proposed method, the host image is decomposed up to 3 levels, i.e.n=3 levels.

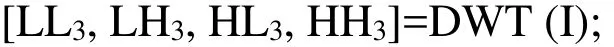
3. Perform Z-Transformation on the sub-band HL3.

4. Apply BSVD on the Z-transformed sub-band of the cover image. The watermark is embedded by modifying the singular values of sub-band with the watermark image.The value of scaling factor (alpha) α is chosen in such a way that the robustness and the imperceptibility of the watermarked image are well adjussted. In this experiment,the value of alpha is taken as 0.2.

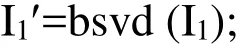
5. The inverse Z-transform is performed on the modified frequency sub-bands as follows:

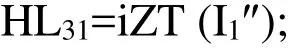
Repeat Steps 2-5, for the sub-band HH3to embed the other half of the watermark.

Apply the 3-level inverse DWT using the modified coefficients HL31and HH31, to generate the watermarked image I'.

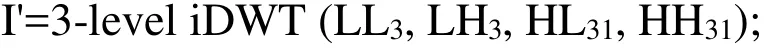
3.2 Watermark extraction scheme

The watermark is extracted using the keys generated during the embedding process. The steps for extracting watermark are given below:

1. The watermarked image I' is decomposed into sub-bands by applying 3-level DWT

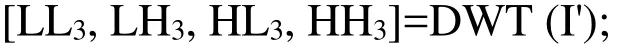
2. Z-transform is computed for the sub-band HL3;

3. Apply BSVD on I’1and calculate D1by subtracting the singular values from the keys generated during the embedding process and dividing the values by the scaling factor (alpha) α as follows:

4. The above steps are repeated for the sub-band HH3to compute W2', which is the second half of the watermark image. The values W1' and W2' are combined, and the watermark image is generated by applying Arnold Transformation.

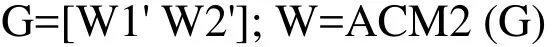
where, W is the extracted watermark.

4 Experimental results and analysis

Watermarking algorithms are generally evaluated in terms of imperceptibility and robustness. Imperceptibility is the measure of indistinguishable between the original and embedded images. In other words, there should not be any difference to view between the original and watermarked image. Robustness is the measure of a watermark to resist against intentional and random attacks.

Several experiments using image processing and geometric attacks were carried out to verify the invisibility and the robustness of the proposed watermarking scheme. The tests were conducted using MATLAB software on standard test images of size 512×512,namely Lena, Baboon, Barbara, Boat (Bridge), Peppers, Jetplane, Man (Pirate) and a logo grayscale image of size 64×64 is used as the watermark (shown in Fig. 1).

The invisibility of the proposed scheme was carried out by considering two parameters as follows:

4.1 Peak Signal Noise Ratio (PSNR)

4.2 Structural Similarity Index (SSIM)

The test images after embedding the watermark logo and the extracted watermark logo from each of the test images are shown in Fig. 5. The efficiency of the proposed method is evaluated by computing PSNR, SSIM, Image Fidelity, Entropy and CC.

Figure 1: (a-f) original host images; (g-l) original watermark images (m-r) watermarked host images (s-x) extracted watermark images

Table 1: PSNR Values obtained (without attacks)

Table 2: Comparison of PSNR values of the proposed scheme with different schemes

4.3 Robustness to attacks

The robustness of the proposed scheme was evaluated by applying various image processing attacks which includes common image processing attacks such as Gaussian noise, salt & pepper noise, Average filtering, median filtering, Blurring, Histogram Equalization, Gamma Correction and geometric distortions like scaling and rotation.

4.3.1 Filtering attacks

The most common signal processing attack is filtering. The watermark is extracted from the watermarked images after applying average and median filters of sizes: 3×3, 5×5, and 13×13. The results are shown in Fig. 2.

Figure 2: Average and Median Filtering Attacks with 3×3 and 5×5 filters and the extracted watermarks

4.3.2 Noising attacks

Additive and multiplicative noise account for the transformation and the degradation of the images. It also results in degrading the watermark information during the extraction.In this experiment, the watermarked image is subjected to 100% salt and pepper noise and the extracted watermark in Fig. 3 shows the robustness of the proposed algorithm.

Figure 3: Watermarked images with 100% Additive Salt and Pepper Noise and the extracted watermark

4.3.3 Geometric attacks

Geometric transformations or attacks include flipping, rotation, cropping and scaling of images. Cropping of images is the most common geometric attack in real time situations.Cropping is done by removing a part of the image either by hiding or deleting the rows or columns of the image. Much information is lost during this process. In this experiment,the image is cropped to 50% and the watermark is extracted as shown in Fig. 4.

The flipping of images generally does not result in loss of information. The vertically and horizontally flipped watermarked image and the extracted watermark is shown in Fig. 4.

Figure 4: Watermarked images subjected to horizontal flip attack and the extracted watermark

Rotating an image to a certain degree can result in loss of information, making the watermark nondetectable. Fig. 5 shows the watermark extracted, after rotating the watermarked image to 50°.

Figure 5: Watermarked images rotated to 50° and the extracted watermark

Scaling an image involves resizing the image to fit into the desired size. The image is enlarged or reduced, resulting in information loss of the embedded watermark. Two different scaling attacks are considered, and in the first case, the image is enlarged to 1024×1024 and it is again resized to its original size 512×512. Secondly, the image is reduced to 128×128 and brought back to 512×512. The attacked image and the extracted watermark images are shown in Fig. 6.

Figure 6: Watermarked images subjected to scaling and shearing and the extracted watermark

Shearing is also another form of generalised geometric transformation usually combined with scaling and rotation. The watermarked image subjected to shearing and the extracted watermark image is shown in Fig. 6.

4.3.4 JPEG compression

Another common attack or manipulation of images is the JPEG compression of images.The watermarked image is tested using different compression ratios and the watermark shown below is extracted from 80:1 as well as 10:1 compressed watermark image as shown in Fig. 7.

Figure 7: Watermarked images with JPEG compression 10:1 and 80:1 ratio and the extracted watermark

4.3.5 Image-processing attacks

Some of the general image enhancement techniques or attacks include sharpening,histogram equalisation, gamma correction, and motion blur. For sharpening of images attack, the watermark image is sharpened by choosing two scaling factors, 0.2 and 0.9.Histogram equalisation is the intensity-level equalisation of the image, resulting in a higher contrast of the image. It increases or sometimes decreases the image contrast to obtain the histogram of uniform distribution. The results of gamma correction, image sharpening, histogram equalisation, and motion blur are shown in Fig. 8.

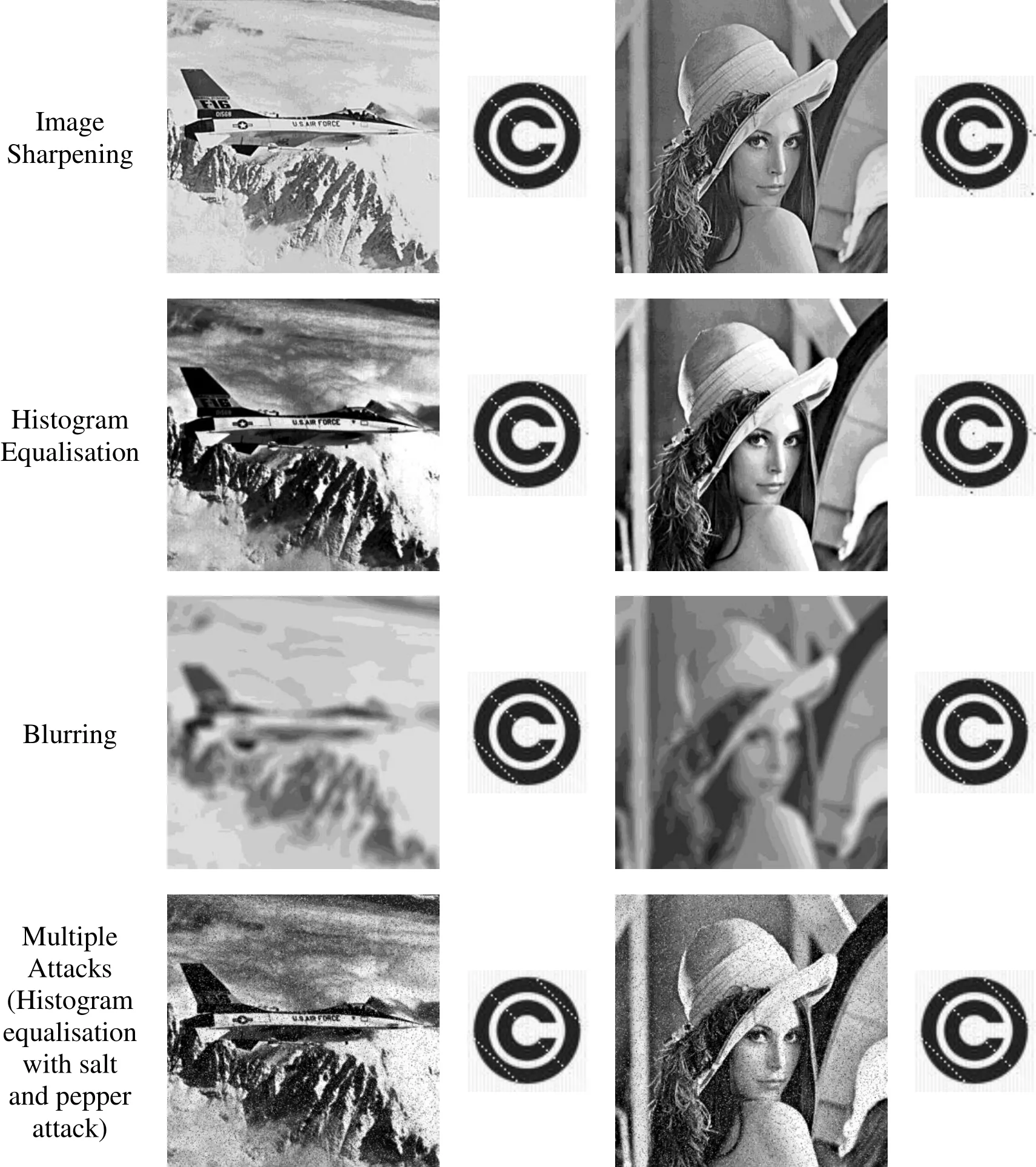
Figure 8: Watermarked images under different image processing attacks and the extracted watermark

The watermarked images are subjected to various image processing attacks, and the watermark is extracted from the attacked image. The correlation coefficients of the original watermark and the extracted watermark are calculated for each attack to verify the ability of the proposed scheme to withstand intentional and non-intentional attacks. Tab. 2 gives the correlation coefficient of all extracted watermarks after the watermarked images are subjected to various kinds of attacks.

4.3.5 False positive attacks

The proposed scheme overcomes the false positive problem by (1) embedding a scrambled watermark (using the Arnold transformation), and (2) the scrambled watermark is divided into two halves and embedded in two different coefficients of the host image. The extracted watermark requires the valid keys and the parameters of the Arnold transformation. From the Fig. 9, it can be seen that the watermark can be extracted with the valid keys and the parameters whereas the watermark cannot be extracted when invalid keys or parameters are provided.

Figure 9: (a) original image, (b) watermarked image, (c) original watermark (d) extracted watermark using correct keys, (e) extracted watermark using the wrong keys

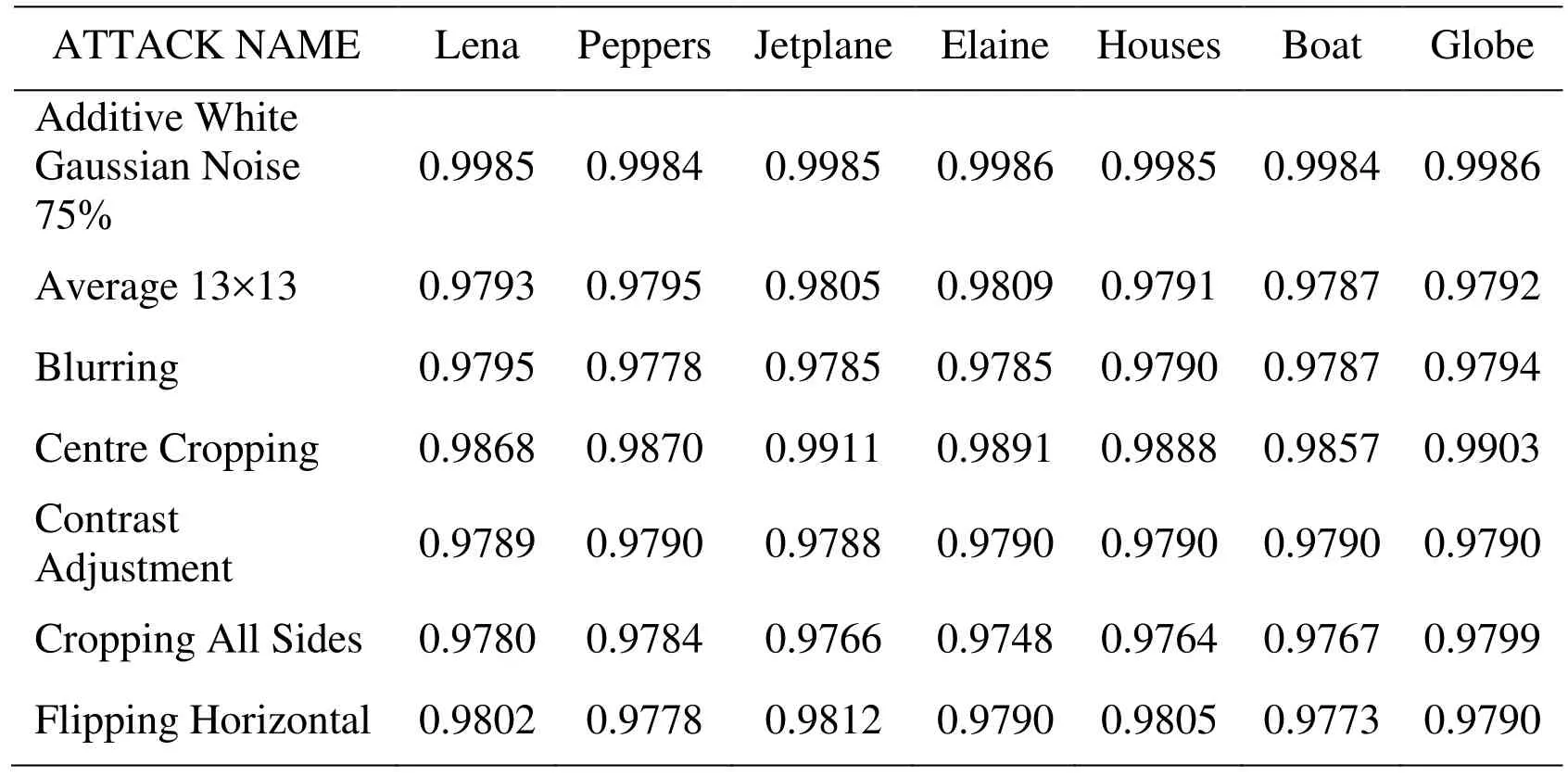
Table 3: Correlation coefficients of the original and the extracted watermark

?

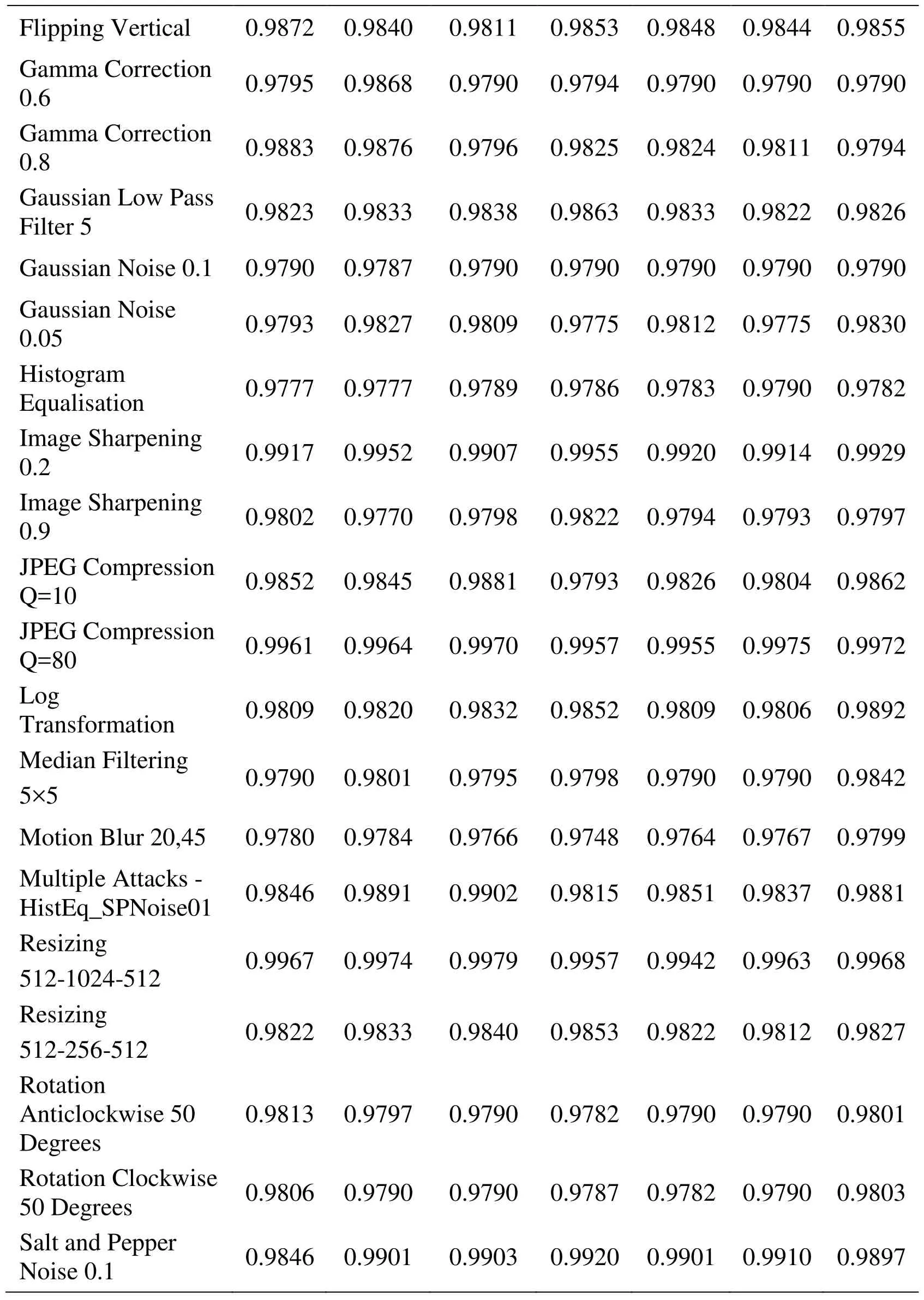
Tab. 3 shows reasonably good CC values against all the signal processing attacks and geometric distortions considered for evaluating the robustness of the proposed algorithm.All these experimental results suggest that the proposed method is extremely robust against common signal processing attacks and geometric distortions.

Comparative study of the correlation coefficient values of the proposed method and the method proposed by Singh et al. [Singh and Singh (2017)] (Tab. 4), Lai et al. [Lai and Tsai (2010)] (Tab. 5), Bhatnagar et al. [Bhatnagar and Raman (2009)] (Tab. 6), and Makbol et al. [Makbol, Khoo and Rassem (2016)] (Tab. 7) are given in Tabs. 4-7. It can be seen that the proposed scheme performs better under various image processing attacks and geometric distortions considered as well as in JPEG compression.

Table 4: Comparison of the correlation coefficients for Bhatnagar et al. [Bhatnagar and Raman (2009)] and the proposed method

The correlation coefficient of the extracted watermark is also compared with the method proposed by Lai et al. [Lai and Tsai (2010)], as given in Tab. 4 below:

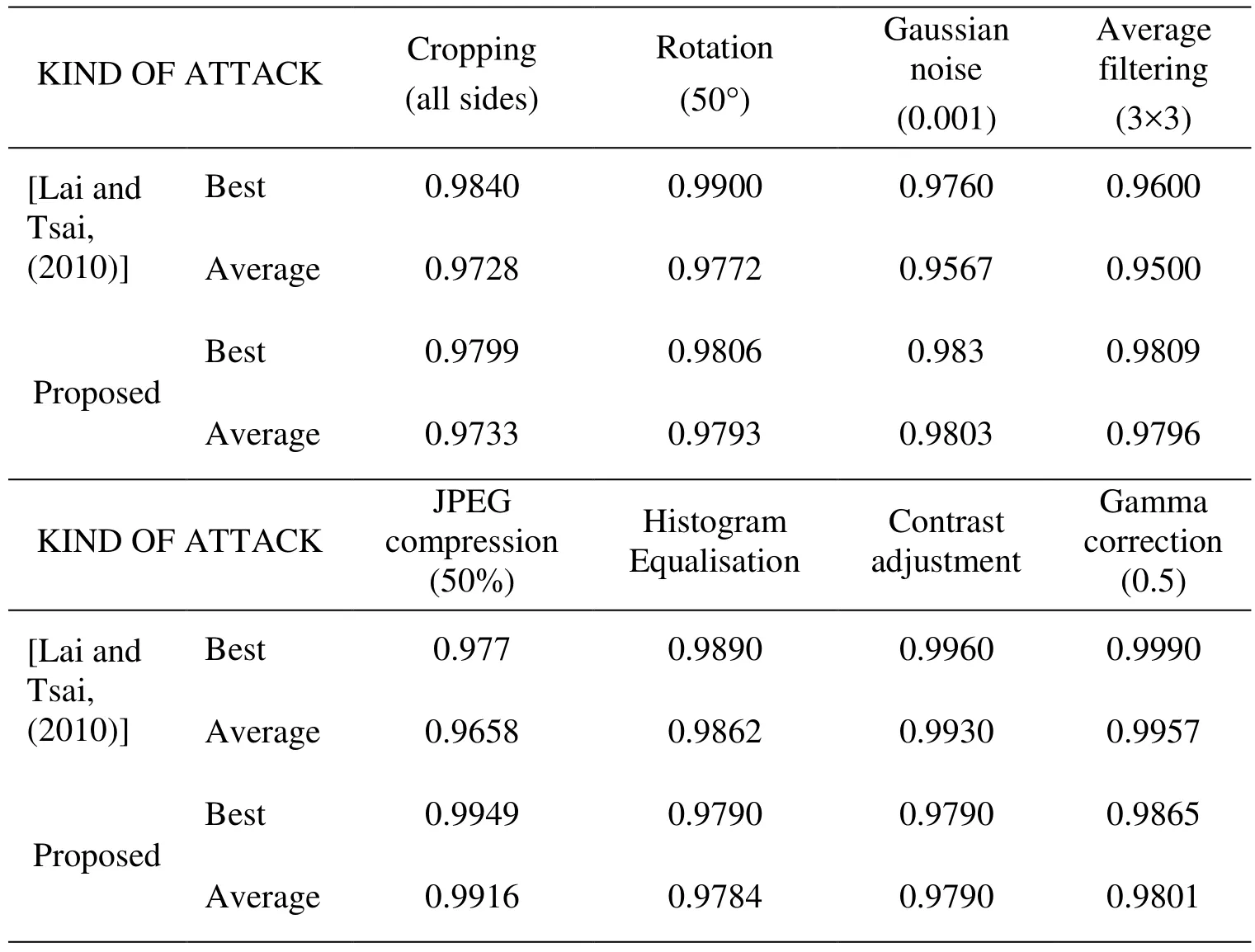
Table 5: Comparison of correlation coefficients for Lai et al. [Lai and Tsai (2010)], and the proposed method

The comparative study of the proposed method with previously reported schemes based on DWT-SVD techniques provided in Tabs. 4-7 shows the proposed scheme combining DWT-ZT-BSVD gives better results.

The proposed scheme is also compared with the scheme proposed by Mishra et al.[Mishra, Agarwal, Sharma et al. (2014)] which is an optimized image watermarking algorithm using DWT-SVD and Firefly algorithm. In their experiment, the authors used two different scaling factors viz. SSF (Single Scaling Factor) and MSF (Multiple Scaling Factor). The proposed method implements a single scaling factor and hence, compared with the correlation coefficient of SSF proposed by Mishra et al. [Mishra, Agarwal,Sharma et al. (2014)]. The comparative results are given in Tab. 8.

5 Conclusion

In this paper, a chaos-based hybrid image watermarking technique has been proposed,based on DWT, Z-transform and BSVD. The scheme combines the benefits of DWT, ZT,BSVD and the chaotic map. Z-transform can efficiently analyze high resolution and narrow frequency spectrum bands, and it has better data hiding properties. The zeros of the Z-transform are very sensitive to minute changes in the pixel values. Hence it is widely employed in fragile watermarking and image authentication applications. The proposed algorithm combines the properties of Z-transform with the widely-adopted DWT to design a robust watermarking scheme. This algorithm concurrently utilizes two sub-bands of the DWT decomposition viz., HL and the HH. The scrambled watermark is divided into two equal blocks, and they are separately embedded into the HL and HH sub-bands, thereby enhancing the robustness. The watermark is embedded in singular values of the bidiagonal SVD, which gives better performance than implementing SVD21.Further, the use of Arnold-Cat map for scrambling of the watermark image before embedding improves the security as the extracted image need to be decrypted correctly to obtain the watermark. Experiments were conducted using standard test images, and the results were analysed for imperceptibility and robustness. The PSNR, CC, Entropy,Image Fidelity and SSIM values of the experiments show that the proposed scheme is more secure and robust.