Estimating the Number of Posts in Sina Weibo
Kai Dong , Taolin Guo Xiaolin Fang Zhen Ling and Haibo Ye
Abstract: Sina Weibo, an online social network site, has gained popularity but lost it in recent years. Now we are still curious on the number of posts in Sina Weibo in its golden age. Besides checking this number in Sina’s operating results, we aim to estimate and verify this number through measurement by using statistical techniques. Existing approaches on measurement always rely on the supported streaming application programming interface (API) which provides proportional sampling. However no such API is available for Sina Weibo. Instead, Sina provides a public timeline API which provides non-proportional sampling but always returns a (nearly) fixed number of samples. In this paper, we present a novel method utilizing this API and estimate the number of posts in Sina Weibo in its golden age.
Keywords: Sina Weibo, popularity, number of posts, public timeline API.
1 Introduction
Online social network is an emerging trend over the past decade which offer the basic functionalities like friends listing, private messaging, information releasing [Heidemann,Klier and Probst (2012)]. With these features, mainstream social applications each has a large user base. Relying on an existing social network services to provide third party login and various other social networking application programming interfaces (API), the variety of mobile applications is now extremely rich, e.g. game, business, work, etc.
The popularity of a social network is important for the application developers, advertisers,or service providers, to make decisions on whether or not to establish business relationship with this social network service. Moreover, the popularity is also important for users of a mobile application, since the choice of third party user register/login with one certain social network may also mean inconvenience or unavailability of social activities in other social networks.
In this paper, we target at analyzing the popularity of the Sina Weibo (“weibo” is a Chinease word meaning “micro-blog”),which is one of the most popular online social network(OSN)site in the mainland of China and some other regions all over the world.Sina Weibo has experienced an explosion in popularity after its birth in 2009,but also soon lost popularity like many other Internet products and services from 2013 or 2014.However the story is still going on.With the wave of large-screen smartphones,Sina Weibo is now experiencing a steady development in popularity since 2017.This arises our interest in estimating and analyzing the number of posts in Sina Weibo,especially in its golden age in 2014.According to the 2017 full-year operating result of Sina Weibo,the number of monthly active users of Sina Weibo is 392 million(93%of which are mobile users),and the number of daily active users is 172 million.We can obtain the numbers of active users in different years by checking Sina Weibo’s operating results(which is always rising even when Weibo lost its popularity after 2014,e.g.the monthly active users of Sina Weibo in 2015 is 175 million,which grew 36 percent year-on-year).
However,the real popularity of an OSN site is determined not only by the number of active users,butalsoby “thenumberofposts”(i.e.howactivethe“activeusers”are).Thenumber of posts is rarely published by Sina,so we aim to estimate this number by using statistical techniques.
To perform measurement and analysis on an OSN,a large scale data set is critical.Using web crawlers and calling public APIs are the two most common ways to get a large scale of data in OSNs.According to the gradually improved security mechanisms and techniques employed by OSNs,it is always more dif ficult and more expensive to continuously crawl large scales of data from OSNs.As a result,most recent studies rely on public APIs which are of ficially supported,e.g.Lehmann et al.[Lehmann,Gonçalves,Ramasco et al.(2012)]evaluate hashtag popularity by using Twitter’s rest API,Xu et al.[Xu,Zhang,Wu et al.(2012)]examine the abuse of online social networks and Thomas et al.[Thomas,Grier,Song et al.(2011)]analyze user posting behavior by using Twitter’s streaming API.Sina Weibo also provides such APIs,i.e.the public timeline API which returns several posts after being called.
The data returned by calling such APIs is always a real-time sampling of the global data of the whole OSN.However,the dif ficulty in estimating the number of posts depends on the semantics of the API used.Some ofthese APIs can provide proportionalsampling of global data(e.g.Twitter’s streaming API).the measurement on the number of posts is trivial since the global number of posts can be calculated by multiplying the number of returned posts with the fixed proportion.Another form of the APIs can only provide“non-proportional sampling”of global data but always returns a(nearly) fixed number of samples(e.g.Sina Weibo’s timeline API).Estimating the number of posts by using this kind of APIs is quite challenging,sine the global number of all posts and the number of returned posts seem to be irrelevant to each other.
In this paper,we propose a novel method to estimate the number of posts by using nonproportional sampling APIs.This work is based on a large-scale data set which contains 667 million Sina Weibo posts obtained by using the Sina Weibo’s timeline API.By ana-lyzing this dataset,we observe that there are9Sina Weibo test accounts,each of which is releasing posts at their own speed.Intuitively,we can compute the total number of posts released by Sina Weibo test accounts,and we can also count the number of posts released by Sina Weibo test accounts in the data set.This means that we can analyze the real-time sampling proportion by analyzing the sampling proportion of Sina Weibo test accounts,for each time when the Sina Weibo’s timeline API is called,and at last we can estimate the global number of all posts by scaling up the number of returned posts.
This analysis is non-trivial since we still have to deal with statistic errors caused by randomness in sampling.This is because the number of returned posts(i.e.the number of samples)is always moving up and down near the expectation.Further more,the number of posts released by Sina Weibo test accounts is too small in comparing with the global number of all posts,so the distance between the real number of returned posts and the expectation can greatly in fluence the final estimation.To address this problem,we average the sampling proportion in each hour to minimize the statistic error.Our final estimation results show that there are about 1 billion posts per month in Sina Weibo in its golden age from September 2013 to June 2014.
The rest of this paper is organized as follows:Section 2 introduces the data set we used,and Section 3 presents our analysis on the regular patterns of Sina Weibo’s timeline API.In Section 4,we study the global sampling proportion of Sina Weibo’s timeline API,and in Section 5,we estimate the global number of all posts in Sina Weibo.The related work is surveyed in Section 6,and our conclusion to this paper goes in Section 7.
2 Data set
This paper utilizes data from a Sina Weibo real-time post data set which was obtained from Datatang(the biggest data sharing site in China).In this section,we detail a few statistical information about this data set.
The data set contains sampled posts released from September 2013 to June 2014.This data set is collected by calling Sina Weibo’s timeline API periodically,and all duplicate posts are removed.This data set contains about 667 million Sina Weibo posts,and each post is composed of post ID,created time,text,source,longitude,latitude,user ID,re-post count,comment count,location,followers count,fans count,posts count,released time,veri fied time,friends count,collected time and user name.
We count the number of posts recorded in data set by day.The details are as shown in Fig.1,about 1 million posts per day are collected from September 1 to December 29 in 2013,and this number is suddenly increased to about 3 million since December 30,2013.In addition,no data is collected on September 19 to 22 in 2013 and on January 20,2014.So the data we used is not perfect,and this increases dif ficulty in our work.
In the following,we study the sampling rules of Sina Weibo timeline API from this data set.Firstly,we show the distribution of the number of samples for each time this API was called.Secondly,we study the duplicate samples between/among multiple times when calling this API.Lastly,we analyze the stability issues of the sampling procedure.

Figure 1:The number of posts in data set within different days
2.1 The number of samples
The Sina Weibo timeline API is in essence a routine which performs sampling on the real time posts,and returns the sampled results to its caller.It is necessary to examine the number of posts(samples)for each time when this API was called to study the sampling ability.
Wenoticethat,varioussamplescanhaveasametime-stamp.This meansthatthesesamples are returned from the same time calling the API.According to this feature,we count the number of posts returned from each time calling the API by month.The distribution of the numbers of returned samples is as illustrated in Fig.2.For most times when calling the API,the number of returned samples is between 190 and 200.The peak of the distribution shows that the number is most probably around 195 to 197.This number is a little bit different from the of ficially published number of 200 according to the Sina Weibo API documents.
Although the proportion is small when the number of returned samples ranges from 1 to 190,this situation really exists.It is dif ficult for us to verify why the number of returned samples can be so different.We guess that this is caused by some prede fined limitations in the sampling procedure.Fig.3 illustrates as an example all the posts collected between 02:20:30 to 02:31:00,September 1,2013.The time stamps of the collected posts appear repeatedly in pairs,and the time interval between each pair is 1 s.
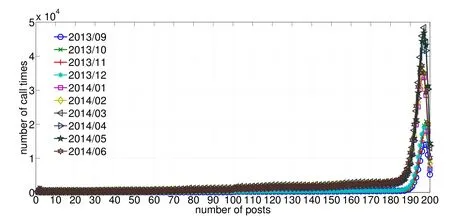
Figure 2: The distribution of the number of collected posts by calling Sina Weibo timeline API once
More importantly, the total number of posts in each pair is near to 200. As a result, we treat the pair of the collected time stamps instead of a single one, to indicate that the Sina Weibo timeline API was called for one time.
2.2 Duplicate samples
Each time when Sina Weibo timeline API is called, it will return at most 200 posts, which are sampled from Sina Weibo real time posts. It is inevitable that there are duplicate samples among multiple times calling the API within a very short period of time. In most cases, the duplicate posts are useless to online social networks analysis. Due to this reason,the data set does not maintain the duplicate posts, and it only maintains what we called theuniqueposts, i.e. the posts have never been previously sampled before. As a result, it turns out that the number of recorded posts in our data set is often smaller than is should be. Fig. 4 illustrates the monthly average number of unique posts returned by calling the Sina Weibo timeline API. The general value of this number is about 160 to 180, which is smaller than 200. We should notice that the value in 2014 are less than that in 2013. The reason is that, since the calling frequency in 2013 is lower than that in 2014 (as illustrated in Fig. 1), the number of duplicate posts (which have been deleted in the data set) in 2013 is also smaller that in 2014.
To further understand the reasons of duplicate samples, we details how the posts in the data set are collected from 00:10:00 to 00:20:00, 1 September 2013, as illustrated in Fig. 5. By calling the Sina Weibo timeline API once, it will generate about 190 to 200 Sina Weibo posts in a short time period (in the past minutes). However, the time periods with multiple times calling the API can overlap, resulting in duplicate samples. As shown in this figure,several sampling time periods have overlaps from 00:10:00 to 00:20:00 on September 1,2013.Take three time periods labeled as 00:14:02, 00:14:20, and 00:14:38 as examples,each of the time period relates to a different time calling the API, the released time of the posts returned are concentrated from 00:13:50 to 00:13:57.
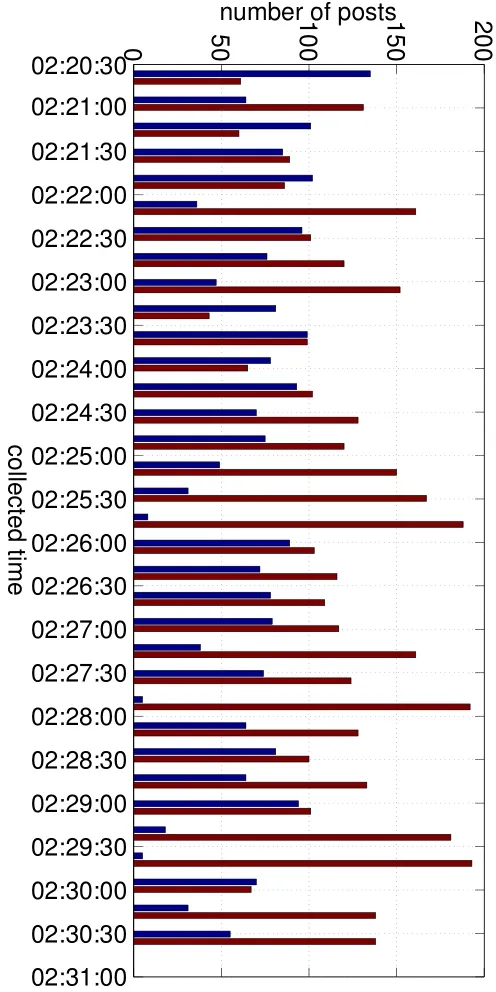
Figure 3:Number of posts collected from 02:20:00 to 02:30:00,September 1,2013

Figure 4:The average number of unique posts returned by calling Sina Weibo timeline API once
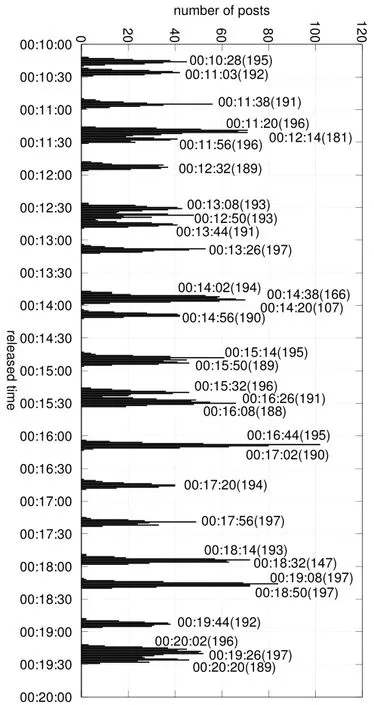
Figure 5: The distribution of the number of unique posts from 00:10:00 to 00:20:00,September 1, 2013
For the first calling (in the first time period), there are 194 posts returned at 00:14:02 and all of them are unique posts and are recorded in the data set. It is a relatively large number since there was no time period overlapping, means that there is no duplicate posts. For the second calling, some posts returned at 00:14:20 but only 107 posts are unique and are recorded. It is a relatively small number since duplicate posts exists.
2.3 Sampling stability
Unlike proportional sampling APIs which have a fixed proportion. Sina Weibo’s timeline API is a non-proportional sampling API, or in another word, the sampling proportion is dynamic and is determined by the number of posts returned by calling this API which is known and (nearly) fixed, and the total number of posts in Sina Weibo which is unknown and is also our goal.
We define the sampling proportion in calling Sina Weibo timeline API as

whereris the sampling proportion,tis the total number of posts released within the period of time,from the time stamp of the first sampled post returned by calling the API to that of the last one,andcis the number of posts returned by calling the API.We have already shown that the value ofcdoes not change much.Now,we discuss the value oft.
It is obvious that a post can be sampled by calling Sina Weibo timeline API,only if it has been released by its owner some time before.For a given sampled post,we de fine thetime intervalas the period of time from when it is released to when it is collected.In Section 2.1,we show that the numbers of posts returned by calling timeline API are similar.So we can deduce that,the longer the time interval is,the more posts will be released in this time period,which means that a largertand also a smallerr(sincecis nearly constant).

Figure 6:The numbers of callings with various lengths of time intervals
Fig.6 illustrates the distribution of the number of times when calling the API,to various lengths of time intervals in which the posts can be sampled.Only a few callings return posts with a short time interval,i.e.0-5 s.The number of callings which return posts with a time interval with length of 5-10 s has a signi ficant rise.For most callings,the time interval is between 10-60 s,and only few callings have a time interval longer than 70 s.
We now can compute the rate of change of the sampling proportion(which we de fined as the sampling stability),but still we do not know the exact sampling proportion for any given calling of the API.
3 Sampling proportion
To compute the sampling proportion,we have to find a subset of posts satisfying the following requirements:
1.The size of this subset is known;
2.Part of this subset is contained in the data set.
Fortunately,we finally find such a subset,which consists of posts released by of ficial test accounts of Sina Weibo.In this section,we introduce how we find this subset and how we compute the sampling proportion of Sina Weibo’s timeline API.We start by introduce the Sina Weibo test accounts.Then,we analyze the sampling proportion of Sina Weibo timeline API by using the posts released by test accounts.
3.1 Sina Weibo test accounts
Here we show how we compute the sampling proportion of the timeline API. We obtain 9 Sina Weibo official test accounts, the posts of which have the same format,
command_IPaddress_timestamp.
In this paper we name these posts “signals”. For example,openapi_report1 releases a post
UPDATE_10.75.0.130_1414394581.25905,
means thatopenapi_report1 sends a signal, i.e. a command requestUPDATEto 10.75.0.130 at time 1414394581.25905. Sincetimestampis useless in distinguishing signals, we use onlycommandandIP_addressto refer these signals.
To study the regular patterns of Sina Weibo test accounts and their released posts (i.e.signals), we analyze thetimestampof these signals. By computing the interval between two adjacent releasing of each kind of signals, we find that the signals are released at one of three possible frequencies, i.e. once per minute, three times per minute and six times per minute. These signals satisfying:
·The total number of signals are known;
·Some signals are included in our data set;
·Signals have the same sampling proportion with ordinary posts.
So the number of posts released by test accounts can be calculated,and they can be treated as a particular subset to analyze the global sampling proportion of Sina Weibo’s timeline API.
However,a test account may add or delete a certain kind of signals at some point.In this way,we will calculate a false sampling proportion of Sina Weibo’s timeline API.It is necessary to analyze the stability of releasing signals for each test accounts.Our rule de fines whether a kind of signals are stable by using probabilistic methods.For the signals with the lowest releasing frequency,i.e.once per minute,we have

whereris the probability that it is collected in our data set within1day(24hours/day×60minutes/hour=1440minutes/day),pis the sampling proportion of our data set,we first supposepis 0.01,(in fact,the sampling proportion is greater than1%,so we will get a larger value with compare to real probability),and the value ofris about5.2e-07,this is really a small value,and we assume a kind of signal is unstable if there is no such signal is obtained in data set within any time period lasts one day.
For each kind of signals released by test accounts,there are four attributes need to be considered.We list them as follows:
·Whether it is collected by our crawler;
·Whether it is collected in our data set;
·Whether it is assumed to be stable;
·The releasing frequency.
We show some of this detail information in Tab.1.
To ensure estimation accuracy,we choose those signals which last over a month to compose a particular subset.We count the number of posts per minute in this subset by months,and the results are shown in Tab.2.
4 Number of posts
In this section,we detail how we estimate the number of posts in Sina Weibo.We first detail our intuitive method,and show the preliminary estimation results.Then we analyze theprobleminthisintuitivemethodandre finetheresultsbyaveragesamplingprobabilities.
4.1 Intuitive method
The key idea of our method is scale-up,which was veri fied effectiveness to estimate the size of networks.This method is based on the assumption that there is a particular subset and the size of this subset is known to estimator.To put formally,letmbe the size of a known special subsetMof some larger setC,cbe the size ofC,tbe the size of a known data setT,andebe the size of the special subsetEwhich is included inT,we have,

Here,ccan be the number of posts in Sina Weibo which is what we want to estimate.In this casemis the number of signals released by test accounts,eis the number of signals which are collected in our dataset,andtis the size of our data set.
4.2 Dealing with dynamic sampling proportions
However the expectation of the number of posts of an OSN is greatly different at different time due to user activities.For example,there are much more posts in daytime than in nighttime since most users fall asleep at night.To solve this problem,we divide our data set into several sub-period(by hours),and simplify this problem bysupposing that the sampling proportion is similar within a same hour.So the number of posts in each month can be calculated as follows,


Table 1:Details in signals released by Sina Weibo of ficial test accounts.The column with heading(C.)indicates whether a kind of signal is collected by our crawler;the column with heading(D.)indicates whether it is collected in our data set;the column with heading(S.)indicates whether it is assumed to be stable;and the column with heading(F.)indicates the releasing frequency,i.e.the number of posts per minute
Wherecis the number of posts,cijis the number of posts in thej-th hour of thei-th day,mis the number of signals the test accounts should release within an hour,tijandeijare respectively the number of posts and the number of signals released by the test accounts in thej-th hour of thei-day which are collected in our data set,nis the number of days of a month.Using this equation,we show our preliminary results in Tab.3.

Table 2:The number of posts in the particular subset per minute
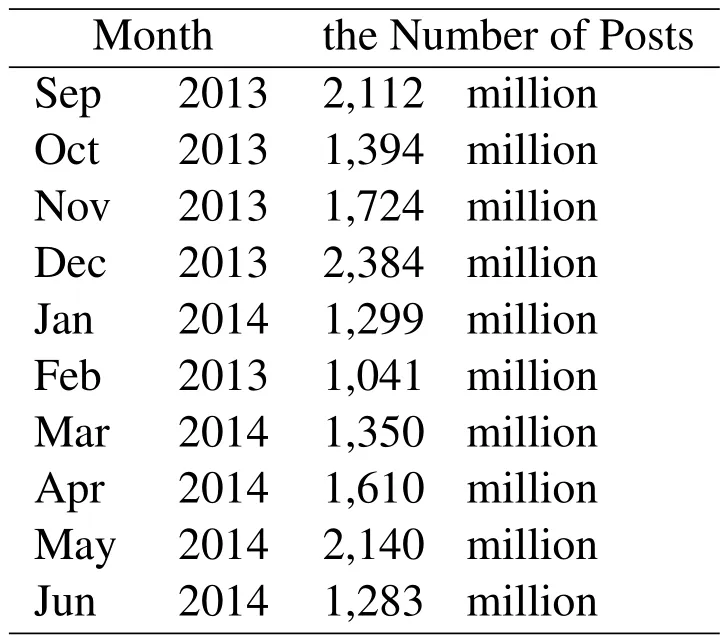
Table 3:The(preliminary)number of posts estimated by Eq.4
4.3 Dealing with errors caused by samplings
The number of samples can move up and down around expectation due to the heart of randomness,and the distance between the real value and the expectation can cause deadly errors when the sampling proportion is small.As shown in Tab.2,the size of our particular subset is between 48-60 posts per minute,which are 2880-3600 posts in an hour,it is too small in compare with the global number of all posts in Sina Weibo within an hour.So the randomness in sampling will greatly in fluence the accuracy of our estimation.However the average of multiple samples should be close to expectation.So the error caused by sampling can be minimized,by supposing that the sampling proportion is similar within different sub-periods which are in a same hour of different days.Here,we use the averaged sampling proportion in an hour of different days to estimate the number of posts in Sina
Weibo.Our re fined method can be formalized as follows,

Wherecis the number of posts we want to estimate,ciis the average number of posts in thei-th hour,mis the number of signals the test accounts should release within an hour,eiis the averaged number of posts in our data set in thei-th hour, andtiis the averaged number of posts in thei-th hour in our data set,dis the number of days in a month.

Table 4: The number of posts estimated by Eq. (5)
4.4 Bound analysis
We now give an insight into our results.We divide our post data set by hour into several subsets and estimate the number of posts in each hour and then add them together.So the determinant of our method is the accuracy of estimation in each hour.
4.4.1 Upper bound
We can treat the signals released by test accounts as a sample of posts of Sina Weibo.Lete1,e2,...,enbe the value of expectations of the numbers of samples for the hours we estimate in thei-th day.For the regular patterns of Sina Weibo users,e1,e2,...,encan be similar,so we set the expectation to beeapproximately.Let the real numbers of samples in the hours we estimate in thei-th day bee+σ1,e+σ1,...,e+σn,whereσiis a variable which describes the error caused by randomness.We have that,for thei-th day,ifσi>0,the estimationcwill be less than the real number of posts,and vice versa.
Without loss of generality,we can assume thatσifollows normal distribution.So we can deduce that,

wherec=m×t/eis the expectation,cu=m×t/(e-‖σ‖)>cindicates an underestimation,andco=m×t/(e+‖σ‖)<cindicates an overestimation.
Based on this formula,we can have following relationship between our estimation results and the real number of posts in Sina Weibo.

Whereciis the estimated number of posts in thei-th hour.This means that the result shown in Tab.3 is the upper bound of the number of posts in Sina Weibo.
We are now using an example to illustrate why the result shown in Tab.3 is the upper bound.Within an hour,the number of posts being sampled is very large,say 10000 is the expectation;however the number of signals being sampled is very small,say 2 is the expectation.As a result,whether a signal is being sampled can greatly in fluence the estimation.Let us assume 1 signal may be sampled or missed,i.e.in a real hour,1 signals or 3 signals may be sampled.We have10000/1+10000/3>10000/2×2.So the result shown in Tab.3 is the upper bound,and the error can be large.
4.4.2 Lower bound
We now analyze the estimation results shown in Tab.4.We assume the number of posts in the same hour of different days to be exactly equal.However this assumption must have errors.Let the average number of samples bee,considering the sampling proportion of different days,the real exceptions in these hours can be represented ase+δ1,e+δ2,...,e+δn.
Let the number of signals released by test accounts bee+δ,we can also deduce that,

wherec′,cp′andcn′arem×t/e,m×t/(e+‖δ‖)andm×t/(e-‖δ‖),indicating our estimated value,and the real numbers which indicate an underestimation and an overestimation,respectively.Also,we have

whereci′is the real number of posts in thei-th hour.This means that the result shown in Tab.4 is the lower bound of the number of posts in Sina Weibo.
We are now using the previous example to illustrate why the result shown in Tab.4 is a re fined version.We make an additional assumption that the number of posts in a same hour of different days within a month is close to each other.So we can combine the same hours of different days together.If a month have 30 days,we have the total number of posts being sampled in these 30 h is expected to be30×10000=300000,and the total number of signals being sampled is expected to be30×2=60.Again we assume 1 signal may be sampled or missed.We have300000/59+300000/61>300000/60×2,and we can find that the error this time is much smaller.
Now we explain why the result shown in Tab.4 is a lower bound.We first ignore in fluence caused by randomness in sampling due to this kind of error in Tab.4 is minimized and very small.Then we should take into consider the difference between same hours of different days.This distance could be very large,as a result,δican mainly caused by this distance(not the randomness in sampling). As the result, the left part in Formula 8 is more describing the real number, and the right part is only an estimation based on a wrong assumption(that the numbers of posts within a same hour of different days are equal). In a word, the result shown in Tab. 4 is the lower bound, and the error is small.
5 Related work
There is little past work on analyzing the number of posts in an OSN, and most social sampling work is related to estimate the size of it. Three methods are commonly used to measure the size of a network.
The first is scale-up, which is based on the assumption that there is a particular subset and the size of this particular is known to estimators; The second is summation, which uses relation types to estimate network size instead of countable subset, since in many cases,it is dif ficult to obtain a countable particular s ubset. McCarty et al. [McCarty, Killworth,Bernard et al. (2001)] compared this two methods for estimating the size of personal networks, and they found that both methods are valid and reliable. The third is graph traversal,the heart of which is a summation method based on the relationships between nodes or on the topology of the OSN.
There is a rich literature on the third method. Cooper et al. [Cooper, Radzik and Siantos(2014)] present a general framework to estimate network properties, e.g. the total number of edges/links, number of vertices/nodes and number of connected triads of vertices (triangles) in graphs, by using random walks. Sinnott et al. [Sinnott and Wang (2017)] analyze the number of individuals in a given area based on geotagged Twitter data. Çem et al. [Çem and Saraç (2016)] estimate the average degree and network size of graphs under a limited data access model called the random neighbor access model. Kimura et al. [Kimura and Tsugawa (2016)] target to estimate the in fluence of social media users, by investigating the effects of node sampling on the in fluence indices. Gjoka et al. [Gjoka, Kurant, Butts et al.(2010)] compared four popular crawling techniques, and they found that compared to traditional algorithms, such as Breadth-First-Search and Random walk, Metropolis-Hasting random walk and a re-weighted random walk performed well. Recent years, graph traversal is frequently used to evaluate social networks properties, such as possible malicious incidents [Haralabopoulos and Anagnostopoulos (2014)] and underlying network structure[Papagelis, Das and Koudas (2013)]. And researchers tried to estimate the size of social networks by this way, Katzir et al. [Katzir, Liberty and Somekh (2011)] and Hardiman et al. [Hardiman and Katzir (2013)] abstracted social networks as undirected graphs and then they using random node sampling to graphs, lastly, they estimate the size of social networks by counting the number of collisions or non-unique nodes.
The work proposed by Fu et al. [Fu and Chau (2013)] is most related to our method in this paper, however, the target of their approach is to estimate the number of users in an OSN and this paper aims to estimate the number of posts. Another related research is in which Hardiman et al. [Hardiman and Katzir (2013)] abstracted social networks as undirected graphs and then use random node sampling on the graphs, and finally can estimate the size of social networks by counting the number of collisions or non-unique nodes. This method is also used to evaluate OSN properties, such as possible malicious incidents [Haralabopoulos and Anagnostopoulos (2014)] and underlying network structure [Papagelis,Das and Koudas (2013)].
6 Conclusion
This paper presents a novel method to estimate the number of posts in Sina Weibo by using data obtained from a public timeline API and public posts released by of ficial test accounts. This API returns sampling results of real-time posts, however the sampling is non-proportional and the number of returned posts is (nearly) fixed. This brings interesting challenges in estimating the number of posts in compare with scenarios when a proportional sampling API is available.
We believe this method is valuable due to two reasons. The first reason is that the legendary history of Sina Weibo which rapidly gained popularity but soon lost it and finally is now developing steadily, has attracted attention of both industry and academia. The second reason is that this method can theoretically compute an upper bound and a lower bound on estimating the number of posts, which can serve as a contrast to the of ficial operating result of Sina Weibo.
Conflicts of interest:The authors declare no conflict of interest.
Acknowledgement:This work was supported in part by the National Natural Science Foundation of China under Grants 61602111, 61502099, 61502100, 61532013 and by the Jiangsu Provincial Natural Science Foundation of China under Grants BK20150628,BK20150637, and by the Jiangsu Provincial Scienti fic and Technological Achievements Transfer Fund, and by the Jiangsu Provincial Key Laboratory of Network and Information Security under Grant BM2003201, and by the Key Laboratory of Computer Network and Information Integration of Ministry of Education of China under Grant 93K-9, and by the Collaborative Innovation Center of Novel Software Technology and Industrialization.
 Computers Materials&Continua2019年1期
Computers Materials&Continua2019年1期
- Computers Materials&Continua的其它文章
- Development and Application of Big Data Platform for Garlic Industry Chain
- GFCache: A Greedy Failure Cache Considering Failure Recency and Failure Frequency for an Erasure-Coded Storage System
- ia-PNCC: Noise Processing Method for Underwater Target Recognition Convolutional Neural Network
- Spatial Quantitative Analysis of Garlic Price Data Based on ArcGIS Technology
- GA-BP Air Quality Evaluation Method Based on Fuzzy Theory
- A Robust Image Watermarking Scheme Using Z-Transform,Discrete Wavelet Transform and Bidiagonal Singular Value Decomposition
