电场对乳化废油双场耦合分离影响的数值分析
龚海峰, 余 保, 戴 飞, 张贤明, 彭 烨,3, 王黎明
(1.重庆工商大学 废油资源化技术与装备教育部工程研究中心, 重庆 400067; 2.重庆理工大学 机械工程学院, 重庆 400054;3.重庆工商大学 机械工程学院, 重庆 400067)
工业废油资源化再利用对于缓解能源短缺、节约资源以及保护环境等具有十分重要的意义,其关键环节是废油乳化液的破乳脱水处理[1-3]。一般情况下,单一工艺方法很难实现乳化油高效破乳脱水处理,将2种及以上的工艺方法或单元操作通过耦合集成,完成常规工艺难以适应的分离过程,是破乳脱水技术发展的主流[4-6]。因此,对于含水量普遍较高、成分复杂的W/O型工业废油,通过以脱水型旋流器为本体嵌入高压电极,生成和耦合电场-旋流离心场,实现废油乳化液高效分离处理[7]。
目前,关于电场-离心场耦合实现乳化油破乳脱水的报道并不多。Bailes等[8]利用高压直流电场和离心场联合完成原油的破乳脱水,并证实电场-离心联合破乳效率要优于电场-重力场破乳。阎军等[9]采用静电场和离心力场联合脱水的新型脱水器对乳状液进行了分离试验,发现高速离心场替代传统重力场,使得破乳效果明显提升。陈海燕等[10]在研究脉冲电场-离心场联合破乳脱水时也发现该技术破乳效果明显。杨秀丽[11]主要研究了离心场和脉冲电场双场联合作用下液滴变形及最佳破乳频率的问题。王健[12]和孙立江[13]也各自对离心-脉冲电场联合作用下旋流场结构对乳化油分离影响规律进行了研究。然而已有研究均未从双场耦合作用的角度分析其对乳化油脱水分离的影响,不能从根本上阐明双场耦合破乳脱水的规律,也限制了技术的推广应用。笔者将着重从双场耦合作用的角度仿真分析电场对废油乳化液分离的影响。
1 双场耦合分离数值模型
以脱水型双锥旋流器为本体结构的旋流腔段内嵌入高压电极电场(如图1),即运用高压电场在短时间内完成乳状液小水滴的聚结,旋流离心场在短时间内实现聚结液滴的沉降分离,从整体上提高乳化油破乳脱水效率,实现废油高效快速脱水[14]。建立旋流离心场-高压电场耦合单元几何模型(如图2),单元结构参数列于表 1。溢流口伸入段外圆柱面和与对应的筒身直管段对应柱面之间形成高压电场,其他区域均为液体区域。

图1 双场耦合脱水单元示意图Fig.1 Diagram of double-field coupling dewatering unit
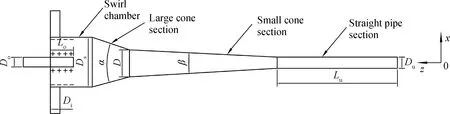
图2 双场耦合单元结构模型Fig.2 Geometry structure of double-field coupling unit

D/mmDi/mmDo/mmLo/mmαβDu/mmLu/mm2612184520°3°10400
油-水混合液流体在双场耦合分离单元中满足如下控制方程:
(1)连续性方程
(1)
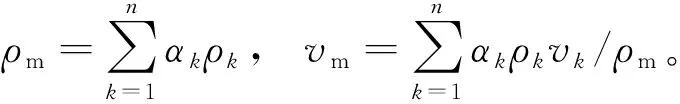
(2)Naive-Stokes方程

(2)
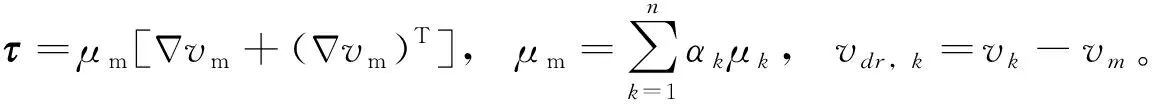
(3)电场控制方程
在电场作用下双场耦合单元物理模型中液滴所受的电场力可由麦克斯韦应力张量[15]表示:
(3)
其矩阵形式为:
(4)
将电场体积力作为外部体积力添加至Naive-Stokes方程中,由于双场耦合单元物理模型采用的是笛卡尔坐标系,因此电场体积力可用fx、fy、fz3个电场体积力分量表示:
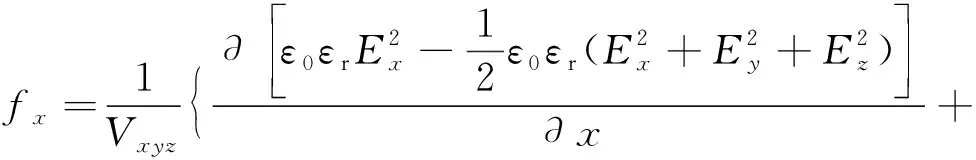
(5)

(6)
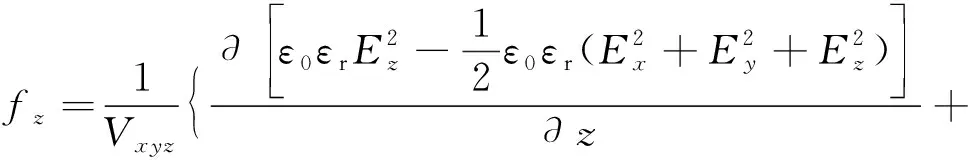
(7)
(4)输运方程

(8)
(5)液滴粒径控制方程
根据Atten液滴成对结聚模型[17],从N个液滴半径为Rw的液滴结聚到0.5N个半径为21/3Rw的液滴,运用Stokes公式计算可得:
(9)
为了确定乳化油液滴在流场中的粒径大小,数值计算得出液滴在电场区段停留时间t,求出t与t1的比值n并取整,然后根据(2n)1/3Rw计算粒径大小。
2 数值计算
2.1 流场条件与网格划分
选用20#机油为连续相,水为分散相,液滴半径Rw为0.1 mm,并设底流口分流比为10%,流场相关参数如表2所示。

表2 流场参数Table 2 Parameters of flow field
由于双场耦合单元是一种细长结构,它的长/径比(925 mm的总长度与26 mm的公称直径之比)较高,约为36。在液体流入底端时流场的梯度非常小,此部分应适当降低网格密集程度。电场与离心场耦合处的网格质量对耦合模拟结果影响最为明显,此部分划分网格时应合理地进行加密处理。另外,入口段与旋流腔相切处的网格应当适当地进行加密以保证网格质量。
对于耦合单元的本体结构,采用自动网格方法,其特点是可以根据体扫掠进行四面体或扫掠网格的六面体网格划分[18]。生成的耦合单元本体结构的三维网格数量为723695个,最大网格扭曲率为0.55,生成的计算网格如图3所示。
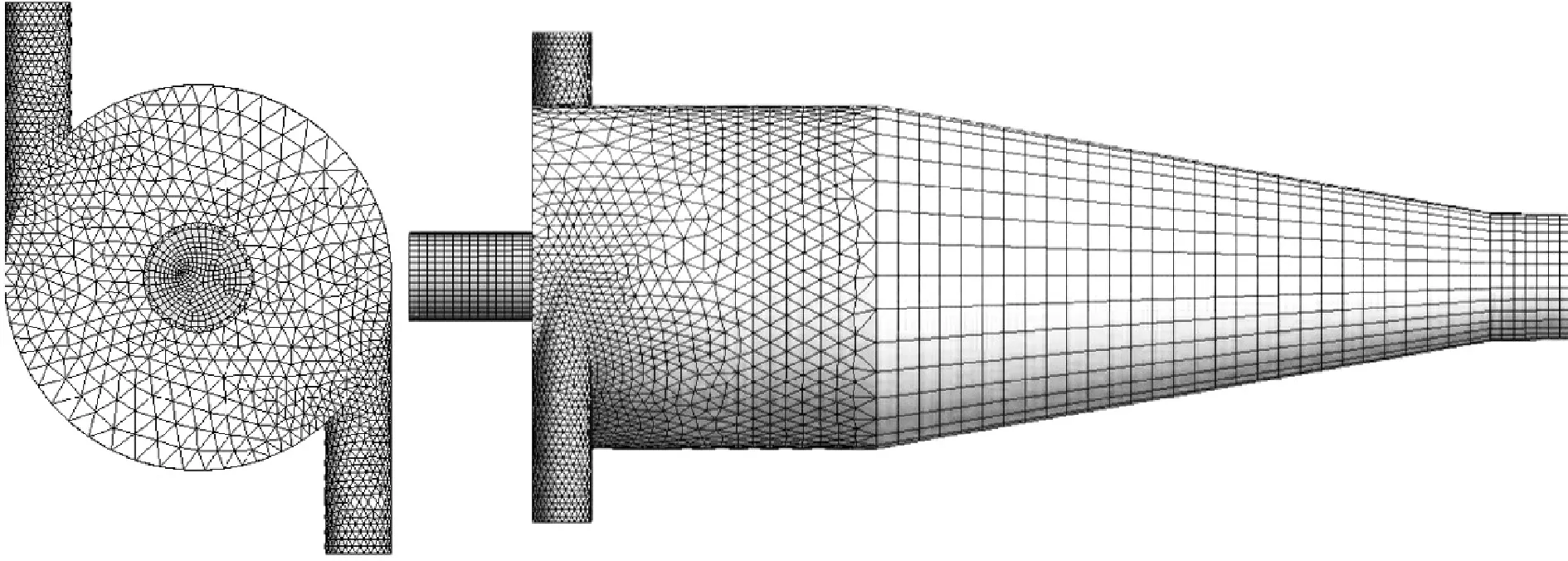
图3 生成的计算网格Fig.3 Computational mesh
2.2 边界条件与计算
设入口边界条件为速度入口,且入口截面法向速度为10 m/s,其他2个方向速度为0;乳化液中含水体积分数为10%;入口湍流强度为5%,入口直径为12 mm。出口边界为自由出口。壁面为无滑移边界条件,采用标准壁面函数对近壁面区域进行处理。设单向直流电场电压幅值为11 kV。溢流管伸入段壁面作为电场高压输入端,旋流腔内壁面作为电场接地端。
笔者采用用户自定义函数方法建立多场耦合单元物理模型的电位方程,基于该方程求解电场强度,通过麦克斯韦应力张量法解出电场力,并将电场力作为源项添加到Naive-Stokes方程中,利用有限体积法控制方程的离散,且设时间步长为0.05 s。
3 数值结果与分析
3.1 速度场分布
为了研究高压电场作用对单元内部流体的流动特性的影响,对比分析了嵌入高压电场作用与离心场单独作用时单元内部的切向速度及轴向速度分布。取4个垂直于本体结构中心轴的横截面进行对比分析,且各截面z轴方向位置分别为z=100 mm、z=620 mm、z=750 mm、z=790 mm。
耦合单元内部流体切向速度在3个速度(分别为切向速度、轴向速度和法向速度)分量中占主导地位,数值上比轴向速度和法向速度大,且由其产生离心力驱动乳化油中水滴向壁面运动。由数值计算得到的耦合单元内部切向速度分布如图4所示。由图4可知,4个截面上的切向速度分布形态基本相同,均出现双峰现象,即在径向位置上出现2个切向速度最大值,且可将其分为外部准自由涡和内部准强制涡。切向速度的最大值出现在准强制涡与准自由涡的交界面;在准自由涡内,切向速度随横截面半径的增加迅速减小,由于壁面采用无滑移边界条件,切向速度值在边壁处的值为零;在准强制涡内,切向速度随横截面半径的增加而增加。
由图4可知,由于高压电场的影响,双场耦合作用在z=100 mm及z=790 mm截面上的切向速度最大值比流场单独作用时的最大速度值略大;在z=620 mm截面上,2种作用下的最大切向速度值基本相同,且该截面上的切向速度分布为非轴对称性,表现为流体旋转中心与单元几何中心不重合,左右两边最大切向速度值大小相差较大。在z=750 mm 截面上,在左半个曲线内2种作用下的最大切向速度值基本相同,在右半个曲线内高压电场作用下的切向速度最大值也同样比流场单独作用时的最大速度值略大。因此,高压电场作用使得单元内部强制涡及自由涡的旋流强度略有增强,更有利于乳化油的脱水分离。
图5为双场耦合作用与单一旋流场作用2种条件下单元内部4个不同截面上的轴向速度分布。由图5可知,轴向速度具有明显的轴对称性。以轴向速度为0的点为分界点,将轴向速度分成内涡流区以及外涡流区。在内涡流区,轴向速度最大值在轴心处,且随横截面半径的增大而减小;在外涡流区,轴向速度随横截面半径的增大先增大后减小。在整个单元内部,轴向速度为0的点形成零轴向速度包络面。
由图5还可知,在z=100 mm截面上,由于高压电场的影响,轴向速度略高于旋流场单独作用时的速度;在z=620 mm、z=750 mm及z=790 mm截面上,2种不同作用下的轴向速度曲线基本重合在一起,无明显差异,表明高压电场基本对轴向速度影响较小,不会对分离效率产生较大影响。

图4 不同截面的切向速度分布Fig.4 Radial distribution of tangential velocity at different cross sectionsz/mm: (a) 100; (b) 620; (c) 750; (d) 790

图5 不同截面的轴向速度分布Fig.5 Radial distribution of axial velocity at different cross sectionsz/mm: (a) 100; (b) 620; (c) 750; (d) 790
在高压电场作用下,耦合单元的y=0截面上的正轴向速度区域及负轴向速度区域云图如图6所示。由图6可知,正轴向速度区域即为内涡流区,流体向溢流口流动;负轴向速度区域为外涡流区,流体向底流口流动。

图6 正轴向速度区域及负轴向速度云图Fig.6 Axial velocity contour of both positive and negative zone(a) Zone of positive axial velocity; (b) Zone of negative axial velocity
3.2 分离效率
为了探讨旋流离心场嵌入高压电场作用对单元分离效率的影响,对比分析了嵌入高压电场作用与旋流场单独作用时的油相体积分数分布。2种不同作用条件下,油相体积分数分布云图如图7所示。由图7可知,在轴线区域的含油体积分数较高,壁面区域的含油体积分数较低,这是因为油中的水滴在不断地向壁面运动,实现了油-水两相分离。在溢流口附近区域的含油量最高(体积分数>90%),且区域面积较大,表明轻质油相在向溢流口流动,又因溢流口的排出流量有限,因此在附近区域聚集了大量的高含油量(体积分数>90%)的流体。由图7(a)可知,高含油量(体积分数>90%)液流在单元各个几何段均有分布,且在直管段区域具有较低含油量(体积分数<20%);由图7(b)可知,高含油量(体积分数>90%)液流主要集中在旋流腔及大锥段,且高含油体积分数区域的面积比流场单独作用时要大,在直管段和小锥段区域内均分布有较低含油量(体积分数<10%)的液流,表明嵌入高压电场作用能够明显有效地促进油-水两相流分离。
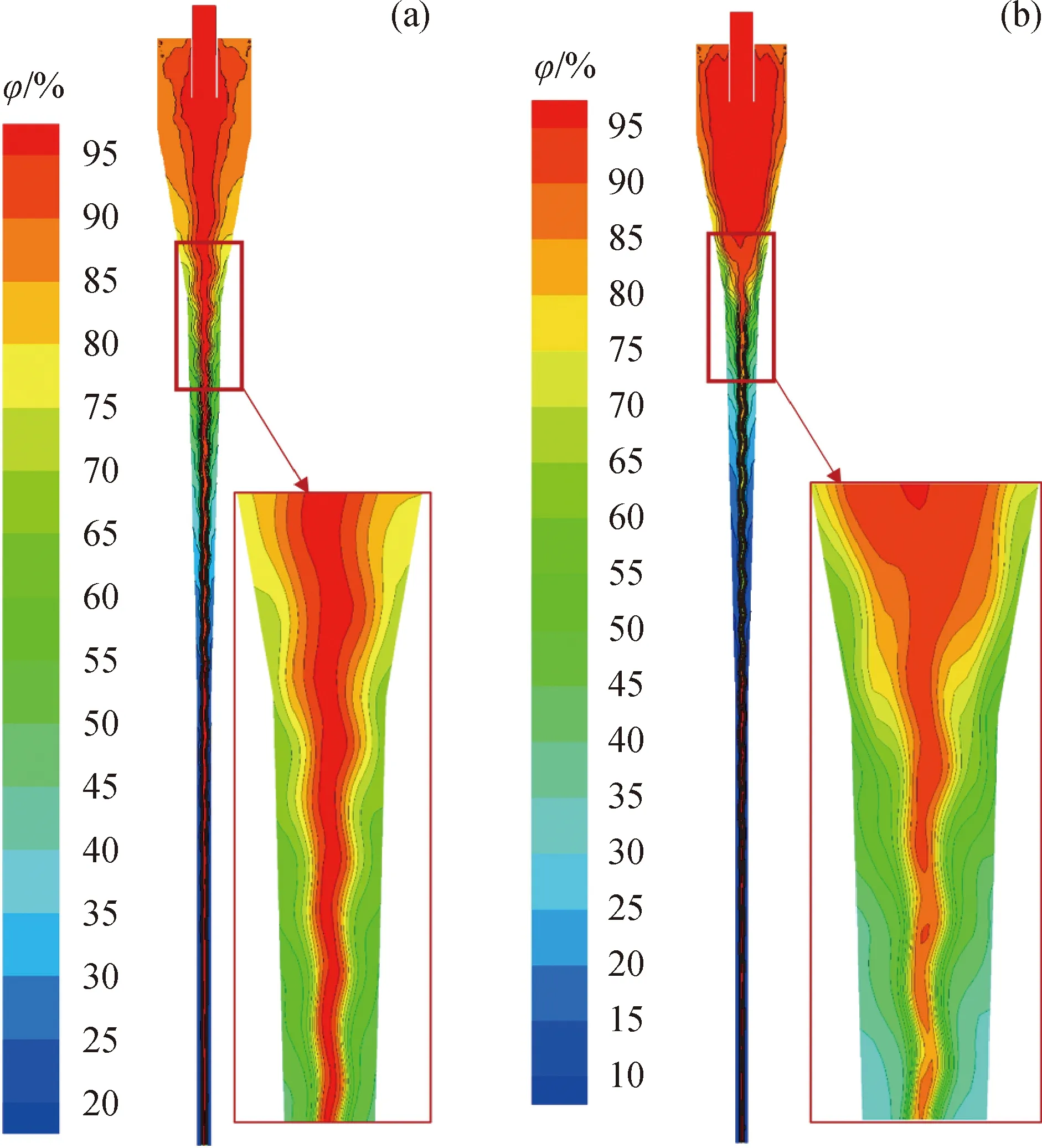
图7 油相体积分数云图分布Fig.7 Distribution of oil volume fraction(a) Single field; (b) Coupling field
为进一步说明嵌入高压电场作用对油相体积分数分布的影响,图8为2种不同作用下4个截面上的油相体积分数分布,油相体积分数呈对称分布,且轴线区域的油相浓度高于其他区域。在z=100 mm 及z=620 mm截面上,嵌入高压电场作用下的油相体积分数明显低于旋流场单独作用,且对于同一油相体积分数,嵌入高压电场作用下的油相分布区域窄于旋流场单独作用。这充分表明,在小锥段及底流直管段,嵌入高压电场能够提高底流口的含水体积分数。在z=750 mm及z=790 mm截面上,对于高含油相(体积分数>96%)的区域,嵌入高压电场作用的分布较宽,且最大含油体积分数值大于旋流场单独作用。这说明了嵌入高压电场作用能够促进油相向溢流口附近区域聚集,提高了溢流口的含油体积分数。
评价分离效率常采用旋流单元溢流口脱水率和底流口脱油率。数值结果表明,在嵌入高压电场和采用单独旋流场2种条件下溢流口脱水率分别为94.3%和80.3%,底流口脱油率分别为86.9%和71.1%。显然,由于高压电场的影响,溢流口的脱水率提高了12.45%,底流口脱水率提高了22.2%。

图8 不同截面处油相体积分布Fig.8 Oil volume fraction at different cross sectionsz/mm: (a) 100; (b) 620; (c) 750; (d) 790
这主要是因为在高压电场作用下油中水滴发生伸缩变形振动,界面膜机械强度降低,微小颗粒水滴在变形碰撞过程中发生聚结,增大了液滴粒径,从而使液滴在离心场中更容易向壁面运动,提高乳化液的脱水效果。同样,根据对流动特性的对比分析可知,高压电场下单元内部轴向速度基本没有变化,切向速度略有增加,对油-水分离有促进作用。因此,旋流离心单元嵌入高压电场能够有效提高油-水分离效率。
4 结 论
利用数值模拟方法研究了高压电场对耦合单元内部流体的流动特性及分离效率的影响,得到如下结论:
(1)通过用户自定义函数法将电场力以源项形式添加到Naive-Stokes方程中,能够实现旋流离心场与高压电场耦合分离计算分析。
(2)旋流器嵌入的高压电场对双场耦合单元内部流场分布影响较小。其中,由于高压电场的影响,切向速度有较小程度的增加,有利于乳化液的油-水分离,而轴向速度无明显变化。
(3)嵌入高压电场对油-水分离有很好的促进作用,提高溢流口的含油体积分数。数值结果表明,旋流器嵌入高压电场后,溢流口脱水率提高了12.45%,底流口脱油率提高了22.20%。
符号说明:
Cij——对流运输项;
D——公称直径,mm;
Di——入口直径,mm;
Dij——扩散项;
Do——溢流口直径,mm;
Du——底流口直径,mm;
E——电场幅值有效值,kV/m;
Ei——i=1,2,3代表沿着x、y、z方向电场强度,kV/m;
Ej——j=1,2,3代表沿着x、y、z方向电场强度,kV/m;
Ex、Ey、Ez——沿着x、y、z方向电场强度,kV/m;
Fe——外部体积力,N;
fx、fy、fz——x、y、z方向电场体积力,N;
g——重力加速度,m·s-2;
Gij——浮力产生项;
Lo——溢流管伸入长度,mm;
Lu——底流管长度,mm;
N——液滴个数;
n——整数0,1,2,…;
p——压力,Pa;
Pij——应力产生项;
Q——入口流量,m3/h;
R——横截面半径,mm;
Rij——雷诺应力项;
RW——液滴半径,mm;
T——麦克斯韦应力张量;
t——液滴在电场区停留时间,s;
t1——液滴成对结聚时间,s;
ui——i=1,2,3代表沿着x、y、z方向的速度,m/s;
uj——j=1,2,3代表沿着x、y、z方向的速度,m/s;
va——轴向速度,m/s;
vdr,k——第k相的飘移速度,m/s;
vk——第k相的速度,m/s;
vm——质量平均速度,m/s;
Vxyz——网格单元体积,m3;
α——大锥角,°;
αk——第k相的体积分数,%;
β——小锥角,°;
δij——克罗内克符号;
εij——黏性耗散项;
ε0——真空绝对介电常数,F/m;
εr——相对介电常数;
μ——油液动力黏度,Pa·s;
μk——第k相的黏性系数,Pa·s;
μm——混合黏性系数,Pa·s;
μo——油相动力黏度,mPa·s;
μw——水相动力黏度,mPa·s;
ρk——第k相的密度, kg/m3;
ρm——混合密度,kg/m3;
ρo——油相密度, kg/m3;
ρw——水相密度, kg/m3;
τ——剪切应力张量, Pa;
φ——油中含水体积分数,%;
φij——压力应变项。

