车辆行人事故碰撞速度重建技术研究

车兴平，谢静茹，黄 云，明健雄，邱金龙，赵 辉

（陆军军医大学第三附属医院野战外科研究所车辆／生物碰撞安全重庆市重点实验室，重庆 400042）

2016年，我国发生车辆与行人交通事故48 006起，造成16 525人死亡，40 114人受伤。事故起数和死亡人数占比达22.55%和26.19%［1］。行人作为弱势交通参与方，损伤严重度较高，根据交通事故数据统计，行人事故的重伤和死亡比例达80%［2］。车辆行驶速度的准确重建对事故责任认定、保险理赔、人体损伤生物力学研究具有重要意义。相较于其他类型的交通事故，车辆行人事故现场痕迹、车辆变形痕迹、散落物较少，加之驾驶员采取制动、避让措施和行人本身的应急反应，使得行人事故车速准确重建仍具有较大的难度和不确定性。

目前车辆行驶速度重建通常按照国家标准GB／T 33195—2016《道路交通事故车辆速度鉴定》实施，其中包括制动痕迹法和行人抛距法。制动痕迹法是根据轮胎在地面留下的制动拖印、压印或侧滑痕迹进行计算，但由于现有的车辆普遍配备ABS系统，事故现场往往难以留下明显的制动痕迹。行人抛距法是根据碰撞点与人体最终停止点的距离计算车速，由于行人事故现场散落物、路面痕迹少，难以确定碰撞点的位置，而且现有方法只适用于卷绕抛射和向前抛射［3］，因此行人抛距法的应用范围也很有限。

除了上述两类方法外，许多研究者也利用新技术、新方法对车辆行人事故车速重建进行了研究。有学者根据行人与挡风玻璃、灯罩等易碎部件发生碰撞后形成的范围分布场，通过散落物运动方程计算车辆行驶速度，但模型中试验参数需要通过参数拟合确定，鲁棒性较低，因此由拟合参数带来的误差较大［4］。人车事故中，平头车或高速行驶的长头车往往导致人体头部与挡风玻璃发生碰撞，可以利用风窗玻璃凹陷变形深度和裂纹半径计算车辆行驶速度［5］。Jun Xu等［6］基于冲击动力学和薄板理论建立了挡风玻璃凹陷变形深度-碰撞速度模型。刘文君等［7］利用有限元模拟仿真和遗传神经网络，通过行人损伤信息对车辆碰撞速度进行估计。总之方法很多，但有效性并未经过大量真实案例的验证。

包络距离（wrap around distance，WAD）是指车辆前保险杠正下方的地面到行人头部与车辆接触位置所包绕的曲线长度［8］，WAD值显然是与车辆碰撞速度有相关性的，而且车辆与成年行人碰撞后，一般都可以测量到WAD值，这为人车事故车速重建提供了一种新的方法。

事故数据记录器（event data recorder，EDR）也称为汽车中的“黑匣子”，它可以记录丰富的事故信息，包括碰撞前5 s内车辆的行驶速度、碰撞瞬间速度、碰撞过程中速度变化量、采取制动的时间、驾驶员转向操作、安全带是否使用等多项数据。EDR记录的碰撞速度对传统车速重建方法的验证和新方法的研究有重要意义。本文的研究目的是利用采集到的具有EDR数据的人车事故，对行人抛距法的准确性进行验证，并建立基于行人包络距离的车速重建计算方法。

1 方法

1.1 数据资料

通过交通事故深度调查，采集具有EDR数据的典型人车碰撞事故案例。典型案例定义为车辆与行人接触后，行人运动状态为卷绕抛射和向前抛射的事故，排除侧面刮撞、人从车顶翻过和碾压等非典型事故。数据来源于重庆市八益交通事故司法鉴定中心、重庆市交巡警总队和重庆市交通行政执法总队。采集的信息包括EDR数据、制动痕迹长度、行人抛距、行人身高和WAD值。统计学分析采用SPSS18.0软件进行，检验水准α＝0.05，以P＜0.05为有统计学意义。

1.2 WAD标准化

为消除行人身高对WAD值的影响，定义包绕比（wrap-around ratio，WRR）为 WAD值除以行人身高，计算公式如下：

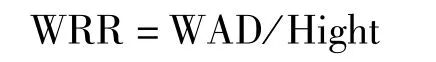
1.3 行人抛距计算模型

行人抛距法计算模型来源于国家标准GB／T 33195—2016《道路交通事故车辆速度鉴定》，计算公式如下：

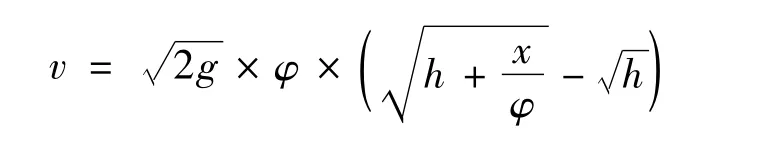
式中：v为交通事故瞬间汽车车速（m／s）；ψ为行人滑动附着系数；x为碰撞接触点到人体质心最终停留位置的直线距离（m）；h为碰撞时行人质心高度（m）。

2 结果

2.1 事故基本信息

采集到27例有EDR数据的典型案例，其中有路面制动痕迹的案例4起；可明确行人抛距的事故11起；可明确WRR值的事故22起。

2.2 抛距法验证

在11起可明确抛距的事故中，排除1起车辆拖行行人导致抛距存在较大误差的案例。计算中沥青路面行人滑动附着系数取1.1，碰撞时行人质心高度取行人身高的0.56倍。经统计分析，抛距法计算误差最大值为24 km／h，最小值为1 km／h，相对误差最大值为36.7%，最小值为1.5%，平均相对误差7.1%（图1）。

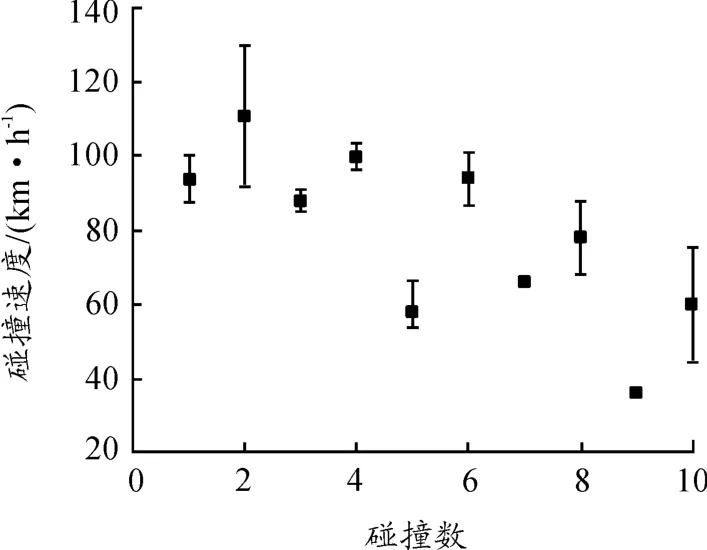
图1 抛距计算方法误差图

2.3 碰撞速度－WRR模型

以碰撞速度为横坐标，WRR为纵坐标绘制散点图，图2（a）表明随碰撞速度增加，WRR值增加，两者之间具有明显正相关性，Pearson相关系数r＝0.65。将车辆按照车型不同分为轿车组与SUV组，图2（b）显示不同车型分组间具有差异，在相同的碰撞速度下，轿车组WRR值高于SUV组。

对轿车组和SUV组分别进行曲线拟合，结果表明：轿车组Pearson相关系数 r＝0.74；SUV组Pearson相关系数 r＝0.85（图3）。

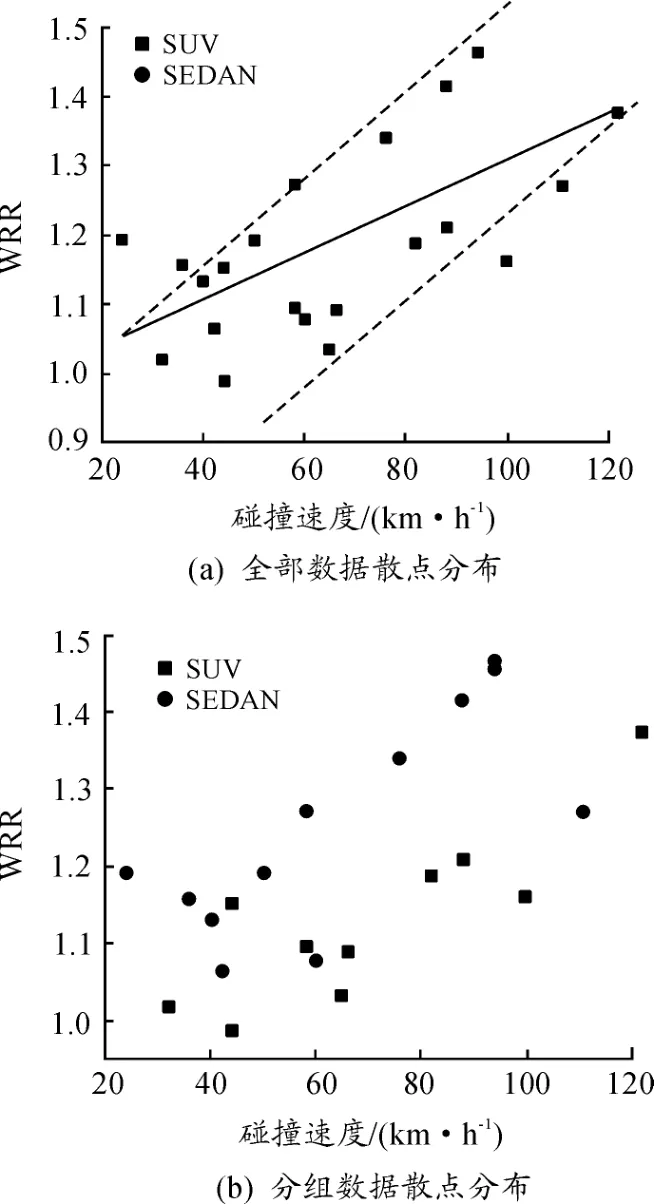
图2 WRR-碰撞速度关系

图3 轿车组与SUV组拟合曲线

以碰撞速度速度（km／h）为因变量，WRR和发动机罩前缘高度（m）为自变量做多元线性回归，建立回归方程：

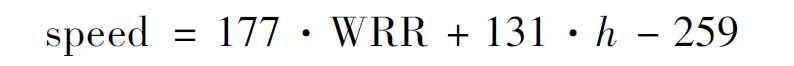
统计结果表明：P＝0.000＜0.05，R2＝0.77，有统计学意义。

3 讨论

在27例人车事故中，4起有车辆制动痕迹，仅占事故总数15%。这是因为行人事故多发生于城市道路，事故车型以小型汽车为主，ABS的作用导致现场很少留下制动痕迹，因此制动痕迹法在多数情况下无法适用。事故中行人抛距的计算依赖于碰撞点的位置，27例事故中，交警部门均无法明确碰撞点的具体位置，只能依靠第一散落物的起点近似作为碰撞点，但也仅有37%的事故可以明确行人抛距。经过EDR数据验证，抛距法平均相对误差为7.1%，最大相对误差达36.7%，在交通事故司法鉴定领域，车速的准确重建涉及到责任认定，这样的结果也是不够理想的。而典型人车碰撞中，均可以通过车辆勘察确定WAD值，因此包绕率法具有更广泛的应用范围。

WRR值与碰撞速度具有相关性，随碰撞速度增加，WRR值增加，其他研究者通过尸体实验和计算机模拟仿真实验也得出了同样的结论［9-10］。但同时发动机罩前缘高度也是影响碰撞速度计算的一个重要参数，经过对不同车型进行分组拟合后，轿车组和SUV的相关系数分别提高到了0.74和0.85。说明经过车型分组后，拟合效果更好，并且在相同的碰撞速度下，发动机罩前缘高度较高的车型导致的WRR值更低。

Feng等［11］根据有监控视频的交通事故对车辆行人事故中WAD与碰撞速度的关系进行了研究，他的研究中未考虑发动机前缘高度的影响，且碰撞发生前驾驶员通常采取了制动措施，因此通过监控视频无法得出精确的碰撞速度值。本研究中车辆碰撞速度直接来源于EDR数据，而EDR记录的碰撞速度误差不超过3 km／h［12］，因此建立的模型具有更高的准确度。前期研究中我们对108例具有EDR数据的案例进行统计发现，事发前驾驶员普遍采取了制动措施，平均制动时间为1.74 s，车辆平均行驶速度由82 km／h降低至63 km／h，因此在后续的研究中可以对有监控视频的事故案例进行修正，来扩大样本数量，有助于建立更高精度的回归方程。

Wood等［13］利用计算机模型对卷绕抛射行人碰撞中WRR与碰撞速度的关系进行了研究。研究结果表明：当碰撞速度小于40 km／h时，WRR与碰撞速度呈良好线性关系，而当碰撞速度大于40 km／h时，随碰撞速度增加，WRR值增加幅度逐渐减小。本文研究表明：当碰撞速度达到100 km／h时，碰撞速度与WRR仍具有较好的线性关系。本研究是基于EDR记录的真实碰撞速度，因此较计算机模拟仿真具有更高的精度。

除了行人身高和发动机罩前缘高度这2个主要影响因素外，质心高度与发动机罩前缘高度的关系也有重要影响。研究表明，成年人在高速碰撞下具有更高的WAD值，但并不适用于儿童假人［14］，这表明在建立WRR-碰撞速度模型的时候还应考虑质心高度是否高于发动机罩前缘高度。因此，上述因素对碰撞速度重建精度的影响还需要进一步研究。

4 结束语

本文通过具有EDR数据的27例典型案例对碰撞速度重建技术进行了研究。结果表明，制动痕迹法具有很大的应用限制，抛距法相对误差最大值为36.7%，最小值为1.5%，平均相对误差为7.1%，重建精度也不够理想。然后，研究了发动机罩前缘高度对WRR值的影响，发现在相同的碰撞速度下，发动机罩前缘高度较高的车型导致的WRR值更低，在此基础上建立了车辆碰撞速度与WRR值和发动机罩前缘高度的回归方程，本研究利用EDR数据对典型车辆行人碰撞事故碰撞速度重建方法进行了重要补充。