基于LMI方法的电液舵机动刚度H∞控制器分析与设计

董 胜， 袁朝辉

(西北工业大学 自动化学院，西安 710072)

液压伺服舵机是飞行器飞控系统中的重要驱动装置，是各种稳定系统和增稳系统的执行机构。舵机作为整个飞控系统中的关键性部件[1-2]，对其动态特性有很高的要求，它的一些性能指标，如阶跃输入时的超调量、上升时间；频率特性中的带宽、稳定裕度等都是以从输入指令到输出位移这样一种输入输出的关系来制定的。然而在实际使用中往往这样一些性能指标比较满意的舵机系统仍会出现一些新的问题，经过分析之后发现以上性能指标不够全面，还应当考虑所谓舵机的阻抗特性(或称动刚度)。也可以通俗地称为舵机在动态负载下的“把持”特性。这个特性与所谓气动伺服颤振有直接的关系[3]。动刚度太差则极易引起舵面的颤振从而影响到整个系统和飞机结构的空气动力学特性。

舵机的动刚度与很多因素有关，例如油源压力、油温、油液弹性模量、作动器本身结构参数等。因此很有必要建立舵机的动刚度实验室仿真模型，详细分析各参数对系统刚度的影响，通过建立的系统模型仿真结果指导舵机控制器的设计，以期在一定程度上提高电液舵机的刚度。

目前电液舵机主要采用各种变结构的PID(Proportion Intergration Differentiation)控制结合前馈补偿驱动伺服阀完成位置闭环[4-6]。本文采用H∞现代控制理论，设计了状态反馈控制器，通过解线性矩阵不等式方程组可以简化控制器的设计[7-8]，理论上指出在LMI(Linear Matrix Inequality)条件下设计的舵机控制器具有比较强的抗干扰能力，系统结构参数波动情况下依然具有较好的控制效果。相对于前馈补偿PID控制，刚度有了较明显的提高，并且刚度幅频特性“凹点”被铺平。舵机在很大的扰动频率范围都能保持较好的抗干扰能力。

1 舵机动刚度特性分析

1.1 舵机动刚度定义

舵机控制系统一般有两个输入端[9]：①控制指令输入端；②外载荷的干扰输入，舵机控制系统除了考虑其位置输出对于指令输入的特性外，还应当考虑位置输出对于外载荷干扰输入的特性，其外载荷与相应位置输出之比称为舵机的刚度，该刚度特性随外载荷频率而变化，如图1所示。

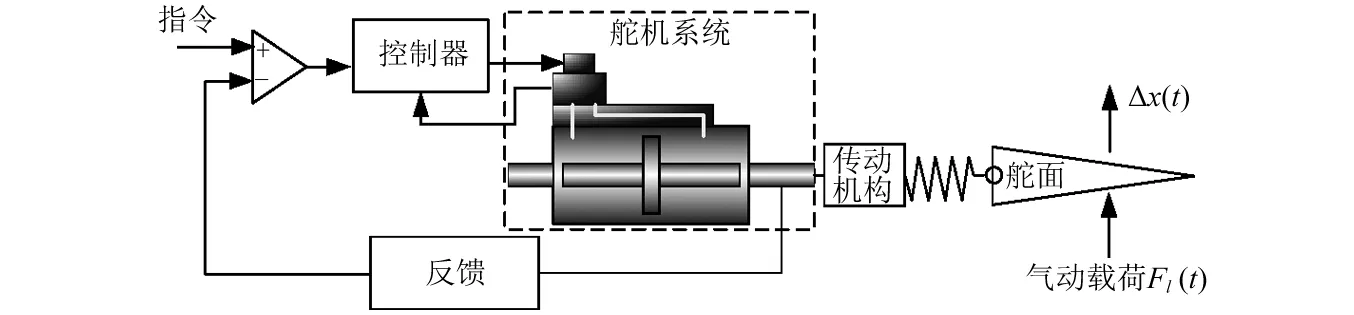
Fl—舵机扰动力;Δx—舵机受扰动作用发生的位移变化量图1 舵机控制系统示意图Fig.1 Schematic diagram of steering gear control system

若假设舵机的输入指令为零，当其负载作用力Fl=0时，输出位移Δx=0，若Fl≠0时，通常Δx≠0。因而Fl/Δx称为舵机的刚度。它的大小体现了舵机控制系统抗干扰能力，动刚度越大抗干扰能力就越强。定义Z(jω)=Fl(jω)/Δx(jω)为舵机的动刚度。舵机的动刚度在复平面上常常表现如图2的形状。

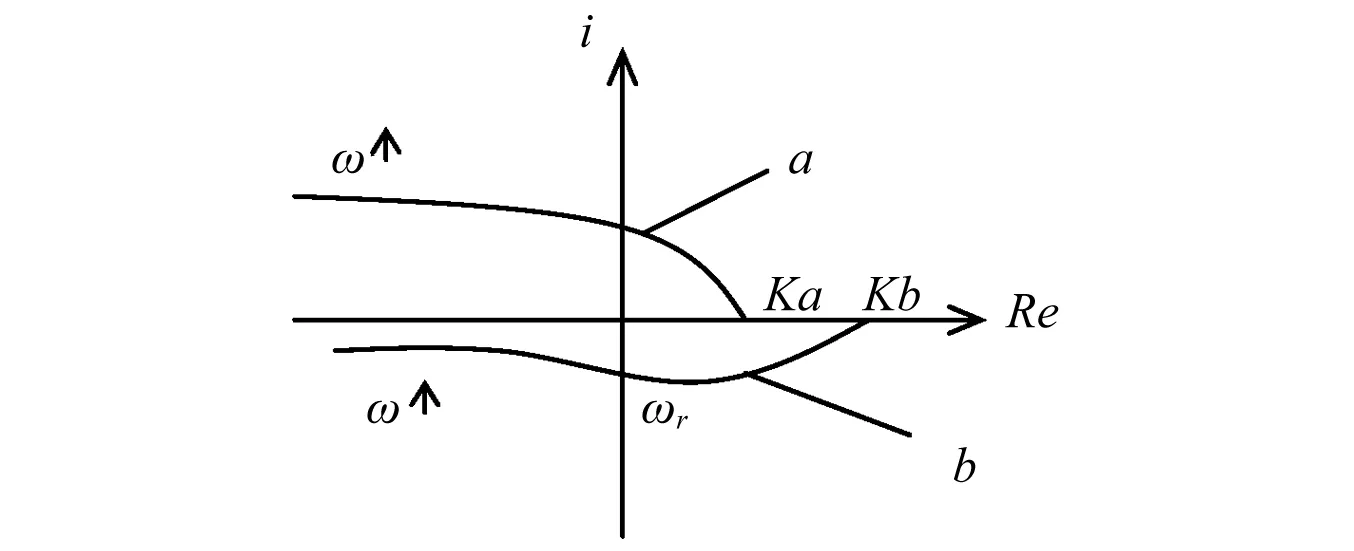
图2 舵机动刚度复频特性Fig.2 Complex frequency characteristic of rudder maneuver stiffness

从图2可知，a的静刚度不如b，但随着ω的增大，曲线a的动刚度下降。而曲线b在某一频率ωr处动刚度非常小，表明在Fl(jωr)作用下x(jωr)较大，也既是此时舵机把握不住它应有的位置，对这样的交变负载没有“抵抗力”，若在此ωr下与气动力相耦合就会发生颤振，引起飞行器故障。

通过建模仿真，图3展示了某型号舵机的动刚度幅频特性曲线，从图3可知，系统刚度特性在频率ωr=103rad/s附近达到最小值。此时系统抑制扰动的能力最弱，需要设计控制器提高舵机在该频率点附近的抗扰能力。

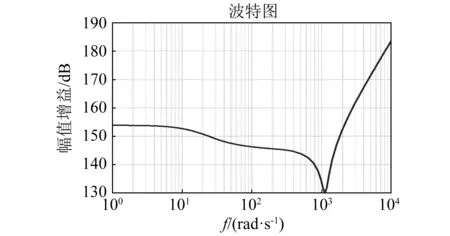
图3 某型号舵机动刚度特性曲线Fig.3 Dynamic stiffness curve of a certain rudder

1.2 电液舵机控制系统建模

将电液舵机系统改变结构，如图4所示。依据此结构的舵机控制系统动力学方程为：

(1)线性化后的伺服阀流量方程[10]

Qf=Kqxv-Kcpf

(1)

式中：Qf为负载流量；Kq为伺服阀流量放大系数；Kc为伺服阀流量压力放大系数；xv为伺服阀阀芯位移；pf为负载压力。

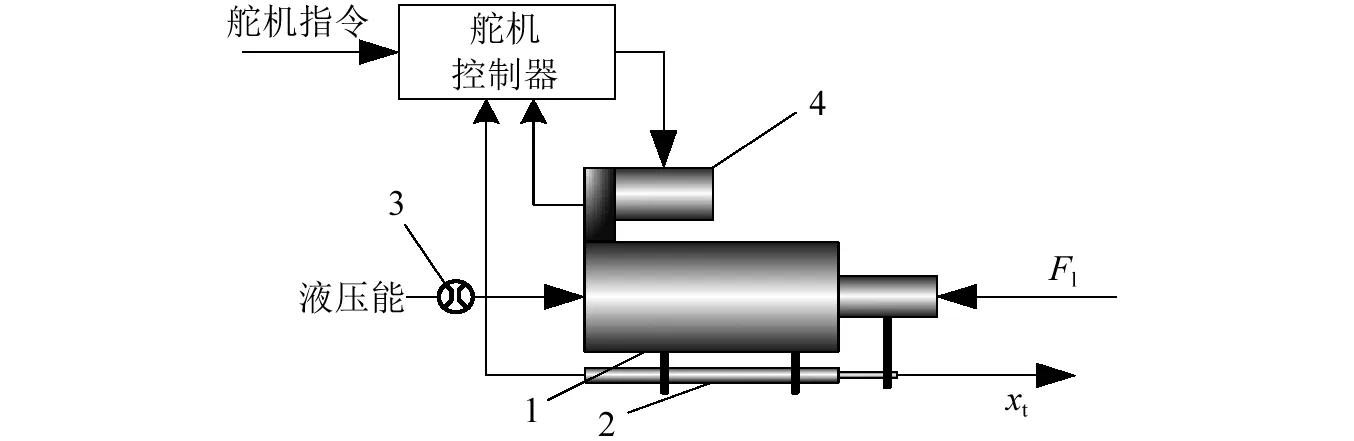
1-舵机；2-舵系统位移传感器；3-舵机能源；4-伺服阀图4 电液舵机控制系统图Fig.4 Control system diagram of electro-hydraulic rudder

(2)舵机液压缸流量连续方程

(2)

式中：At为舵机液压缸活塞有效面积；xt为舵机液压缸活塞位移；Vt为舵机液压缸有效容积;Ey为油液等效容积弹性模量；Csl为舵机液压缸泄漏系数。

(3)舵机力平衡方程

(3)

式中：Fl为外扰动力；mt为舵机液压缸运动部分折算到活塞上的总质量；bt为黏性阻尼系数；Kt为负载弹性系数。

(4)舵机系统电子伺服放大器

u=Kexi

(4)

式中：Ke为控制器放大系数；xi为舵机目标位移；u为控制器输出。

(5)电液伺服阀阀芯位移与控制输入之间的传递函数为

(5)

式中：ξs为伺服阀相对阻尼系数;ωs为伺服阀固有角频率;ksv为伺服阀增益;ki为伺服放大器增益。

对式(1)～式(5)进行拉普拉斯变换并整理，可得系统开环传递函数，如图5所示。

图5 舵机位置控制开环模型Fig.5 Open loop model of steering gear position control

(6)

其中，

Kcs=Kc+Csl

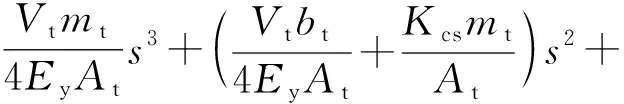
2 基于LMI方法的舵机位置控制H∞状态反馈控制器设计

舵机控制系统的广义结构框图，如图6所示。

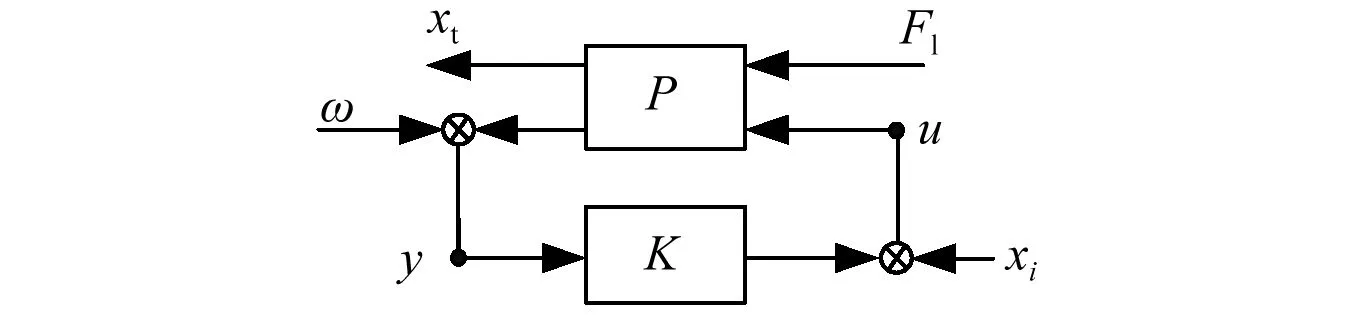
图6 系统广义结构框图Fig.6 Generalized block diagram of system

从图6可知，xi为舵机目标位移；ω为系统测量噪声；y为测量输出;u为控制输入;xt为舵机实际位移；Fl为外扰动力。在测舵机动刚度试验中保持xi恒定或直接为零，忽略ω则图6又可以转换为图7[11]。

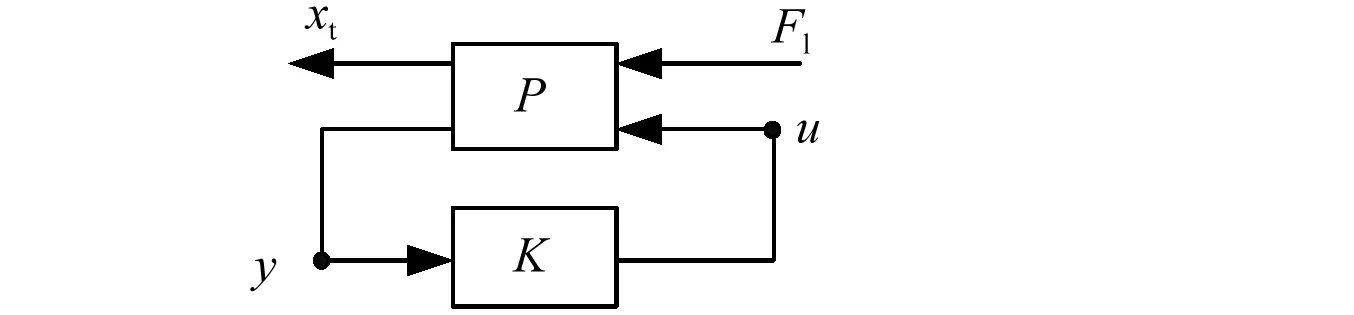
图7 单扰动输入系统广义结构框图Fig.7 Generalized structural block diagram of single disturbance input system

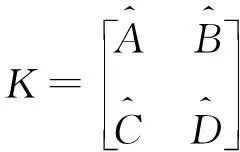
(7)

(8)

那么，K相对于P的一个下线性分解变换为

F(P,K)=P11+P12K(I-P22K)-1P21

(9)

容易知道，图7中Fl|→x的传递函数矩阵TxFl(s)与F(P,K)一致，即

x=F(P,K)Fl

(10)

设计原则1——设一系统中P可以写成式(8)形式。则H∞控制问题是指设计形如式(7)的控制器K满足:

(1) 闭环系统是内稳定的。

(2) 从Fl～xt的传递函数TxtFl(s)的H∞范数满足||TxtFl(s)||∞=||F(P,K)||∞<γ，γ为目标性能。

又因为

(11)

其表征了能量有限输入输出信号的能量放大倍数，设计希望F(P,K)在一定频率范围内能有尽量小的放大倍数γ，问题转化为给定一个γ，设计出来的控制器K能够满足

考虑多输入多输出系统[15]

z=C1x+D11w+D12u

(12)

y=C2x+D21w+D22u

式中：x∈Rn为系统状态；w∈Rl为干扰输入；u∈Rm为控制输入；z∈Rp为被控输出；y∈Rq为可测量输出，假设系统的状态是可测量的，设计一个静态的状态反馈控制器u=Kx使得相应的闭环系统

z=(C1+D12K)x+D11w

(13)

是渐进稳定的且从w|→z的传递函数满足

||Tzw(s)||∞=||(C1+D12K)[sI-(A+

B2K)]-1B1+D11||∞<γ

(14)

可得到状态反馈H∞控制的存在条件和设计方法。设计原则1可以进一步写成：

设计原则2——式(12)存在一个状态反馈H∞控制器,使得闭环式(13)为渐进稳定，且满足性能指标式(14)，当且仅当存在一个对称正定阵X和矩阵Y使得下面不等式成立

如果式(15)有解，则K=YX-1是式(12)的一个状态反馈H∞控制器。进一步基于控制器存在式(15)，通过建立和求解以下的优化问题

minγ

X>0

(16)

可以得到系统状态反馈最优H∞控制器，相应的系统扰动抑制度为γ[16-18]。

3 仿真分析

针对本舵机控制系统将前面建立的系统模型写成式(12)状态空间方程的形式，取

所以有

(17)

进而可以写成如下形式

(18)

参数选取如表1所示，求得

B1=[0 0 1 0 0]T,B2=[0 0 0 0.8 0]T

C1=[1 0 0 0 0],D11=D12=0

表1 系统参数取值Tab.1 System parameter value

依据设计原则2建立起系统的线性矩阵不等式：

lmiterm([1 1 1X],A,1,′s′);

lmiterm([1 1 1Y],B2,1,′s′);

lmiterm([1 2 1 0],B1′);

lmiterm([1 2 2 0],-1);

lmiterm([1 3 1X],C1,1);

lmiterm([1 3 1Y],D12,1);

lmiterm([1 3 2 0],D11);

lmiterm([1 3 3r1],-1,1);

lmiterm([-2 1 1X],1,1)。

结合Matlab LMI工具箱求解函数求得系统的状态反馈矩阵K，将舵机位置指令设置为零，扰动输入采用幅值为1 000 N，频率为100 rad/s，相位为0的正弦函数，

Fl=1 000sin(100t)

如图8所示对比前馈补偿PID控制时的系统输出xt，可以发现相对于没有状态反馈控制时，系统对于Fl=1 000sin(100t)的扰动抑制作用较强，舵机位置环的位置波动幅值减小，而对于系统的脉冲响应，如图9所示。对比H∞控制和PID控制系统的中间状态变量，系统液压缸活塞杆输出位移xt最大波动幅值也相应减小，并且系统各个状态变量的收敛速度加快。

图8 固定频率扰动液压缸活塞杆位置输出Fig.8 Displacement output of piston rod of hydraulic cylinder under fixed frequency disturbance

改变扰动输入的频率，做出扰动Fl到系统输出之间的频率特性曲线，如图10(a)所示，由图10可知：

(1) 状态反馈H∞控制器在舵机实际环境扰动频率10～200 Hz(62.83～1 256.6 rad/s)内[19]幅值放大倍数几乎维持在-206 db不变,相对于PID控制幅值放大倍数(>-150 db)有所减小,相位滞后与PID控制时相当且不随频率的变大而变大，保持在0°不变。

(2) 系统无状态反馈控制时，幅值放大倍数在频率点ωr附近的“上翘”被状态反馈控制器“削平”，不会出现舵机在某一频率附近刚度特性变软的情况。

为了更好的说明系统的动刚度前后变化情况，分别做出Fl(jω)/Δx(jω)的频率特性曲线，如图10(b)所示。无状态反馈控制时在频率546 rad/s求出刚度最小值5.623×105N/m，而加入状态反馈控制后刚度在较大范围内维持1.995×1010N/m不变。

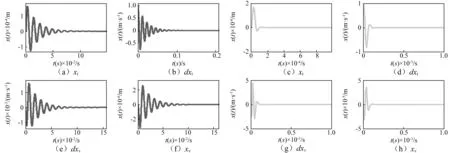
图9 舵机位置控制脉冲响应Fig.9 Impulse response of position control of steering engine

图10 控制效果对比图Fig.10 Contrast chart of control effects

为了验证控制器的鲁棒性使系统油液的弹性模量Ey减小10倍，同样对比系统液压缸活塞杆位移输出xt，如图11所示。减小弹性模量(油液中容解空气量增加)舵机位置环的位置波动都会加剧，相比之下无状态反馈控制时位移波动范围从10-4量级恶化到10-3量级，状态反馈控制后扰动引起的位移波动幅值基本不变。对比系统的脉冲响应曲线，如图12所示。观察系统液压缸活塞杆输出位移xt，xt的导数，xv以及xv的导数等中间状态变化情况，xt最大波动幅值基本不变，并且系统各个状态变量很快收敛。

图11 改变系统油液弹性模量后固定频率扰动液压缸活塞杆位置输出Fig.11 After changing the oil elastic modulus of the system, the position of the piston rod of the hydraulic cylinder output under the fixed frequency disturbance

改变扰动输入的频率，做出扰动Fl到系统输出之间的频率特性曲线，如图13(a)所示。由图13可知:

(1) 状态反馈H∞控制器在舵机真实扰动频率10～200 Hz(62.83～1 256.6 rad/s)内幅值放大倍数维持在-186 db不变，但是比弹性模量减小前-206 db有所变大，相位滞后仍旧不随频率的变大而变大，保持在0°不变。而前馈补偿PID控制扰动幅值放大倍数从很小的扰动频率开始就逐渐变大, 最终增大到-96.9 db。

(2) 系统无状态反馈控制时，舵机对扰动的抵抗能力因为弹性模量的减小而减小。“上翘”频率点ωr也减小到166 rad/s。

分别做出Fl(jω)/Δx(jω)的频率特性曲线，如图13(b)所示。无状态反馈控制时在频率166 rad/s求出刚度最小值6.998×104N/m，加入状态反馈控制后刚度为6.309×108N/m，并在很宽频率范围内保持不变。

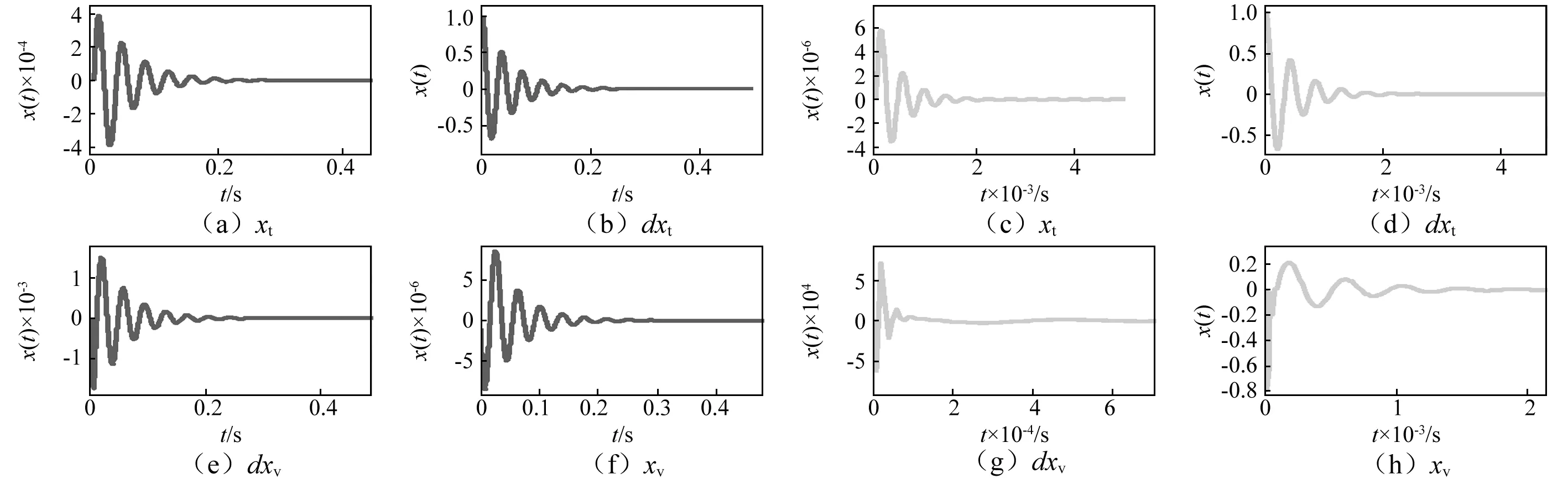
图12 改变系统油液弹性模量后舵机位置控制脉冲响应Fig.12 After changing the oil elastic modulus of the system, impulse response of position control of steering engine

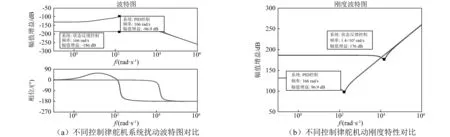
图13 改变系统油液弹性模量后控制效果对比图Fig.13 After changing the oil elastic modulus of the system, contrast chart of control effects

4 试验分析

4.1 试验设计

试验台架分为两个子系统，舵机控制系统和加载系统。舵机控制系统和加载系统作用点之间加装拉压力传感器，通过惯量负载盘模拟实际舵面，系统组成框图如图14所示。加载操作系统平台采用windows系统，通过Lab Windows编程控制加载力。所有位移检测均采用高精度光栅尺测量。通过实际系统搭建测试算法的有效性。实际系统的物理参数与上节仿真参数一致。真实台架如图15和图16所示。

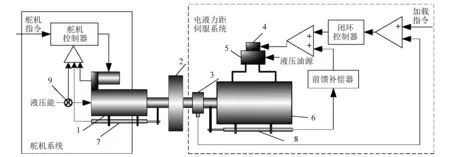
1-舵机;2-惯性负载;3-拉压力传感器;4-电液伺服阀;5-转接阀块;6-加载缸;7-舵系统位移传感器;8-加载系统位移传感器图14 试验系统原理图Fig.14 Schematic diagram of test system

图15 试验舵机Fig.15 Test actuator

系统具体工作原理为：加载系统的函数发生器产生预先给定频率、幅值的正弦信号载荷谱(即参考输入)，在该输入作用下，加载缸产生输出力Fl作用于被试舵机，舵机系统缸将产生一定的位移Δx，加载缸与被试舵机通过连接件固连在一起。加载缸产生的力Fl以及位置系统产生的位移Δx将由传感器测量并通过采集卡转换送入计算机，用以计算出某一频率下舵机位置系统的动刚度特性，计算机完成动刚度的测试和加载系统的闭环控制与校正[20]。

图16 试验舵机加载系统Fig.16 Loading system of test steering gear

4.2 试验结果

试验过程中，加载系统负责施加外部扰动，外部扰动载荷谱为

Fl=-4 340sin(2πft)+4 750

式中：f=20 Hz加载力满足设计要求，跟随曲线如图17所示。舵机做周期为3.33 s，幅值±15 mm的正弦运动，采用第“2”节设计的控制器，舵机位移跟随曲线，如图18所示。舵机位移跟随误差如图19所示。从图19可知，舵机位移跟踪误差波动范围约在±0.1 mm范围内(不包含加载多余力对位置控制的影响)。对比前馈补偿PID控制算法的±0.3 mm本方法起到了一定的抗负载扰动，提高舵机动刚度的作用。

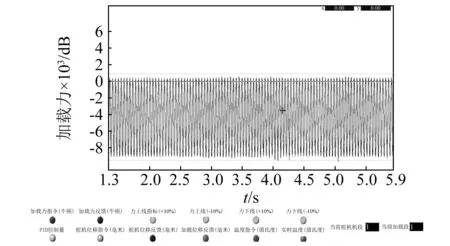
图17 舵机加载系统力跟随曲线Fig.17 Force following curve of servo system loading system

图18 舵机位移跟随曲线Fig.18 Displacement following curve of steering engine

5 结 论

通过对电液舵机系统建模和仿真，可以看到舵机在整个频率范围内会出现刚度特性最差频率点ωr。基于LMI方法设计的H∞控制算法，应用无穷范数的物理意义，在一定的频率范围内系统扰动通道增益最大值不大于性能指标参数γ，保证了舵机回路的动刚度特性。较前馈补偿PID控制抗扰动能力有所提高，并在一定的系统参数波动范围内控制器持续有效，鲁棒性好。在实际的工程项目中该方法也能起到较好的控制作用。