表征驾驶风格和驾驶员能力的驾驶员模型

王超， 郭孔辉， 许男， 张琳， 刘洋， 郑磊， 刘涛

(1. 吉林大学 汽车仿真与控制国家重点实验室，吉林,长春 130025；2. 长春孔辉汽车科技股份有限公司，吉林,长春 130012 3. 中国第一汽车集团公司技术中心，吉林,长春 130011)

在人-车-路闭环系统中，驾驶员兼做道路状况的感知环节和车辆操作的决策环节，对车辆安全稳定的行驶以及乘坐人员的感受起着重要作用. 驾驶员模型从控制的角度，对真实驾驶员的车辆操作行为进行模拟，被广泛应用于车辆仿真开发、主动安全控制系统设计[1-2]及智能车控制系统开发[3-4]. 更准确更真实地反应驾驶员的行为，是驾驶员模型开发的目标之一. 其中DYNAware仿真平台的驾驶员模型以线性单轨车辆模型和半经验轮胎模型构建控制内模，将驾驶员轨迹跟随行为转化为最优控制问题进行求解，轨迹跟随效果较好，并且通过设定驾驶员操作参数和车辆响应参数的极值定义驾驶员风格，仿真中显现出了不同的驾驶方式. 模型预测控制(MPC)由于其滚动更新预测区间进行寻优的特点，与真实驾驶员行为习惯相近，被广泛应用于车辆转向控制行为的建模[5-6]. 模型预测控制被应用于模拟驾驶员学习、自适应车辆特性并进行转向操作决策的行为，设定了几个自由参数以模拟不同的驾驶员，包括视野距离的远近、侧向位移与车身方位角的权重比，并根据22位真实驾驶员的驾驶结果进行了误差统计与分析，更丰富的描述了驾驶员. 基于随机模型预测控制建立驾驶员转向行为模型，应用侧向横摆二自由度车辆模型与UniTire轮胎模型[7]建立预测模型，将驾驶员对轮胎侧偏角的估计以正态分布的形式建模，表征熟练驾驶员与生疏驾驶员的估算差别.

尽管上述文献对驾驶员的驾驶方式进行了一定区分，但真实驾驶员面临驾驶环境复杂多变，且不同驾驶员对车辆操纵能力也不尽相同. 因此，本文基于最优预瞄理论，通过4个自由参数表征：驾驶员的视野范围大小、远近重视程度、决策意愿、决策精度差异. 从而丰富了模型对驾驶员的驾驶风格及驾驶员能力的模拟.

1 驾驶员的视野特征与决策意愿建模

真实驾驶员的驾驶习惯往往是关注视野中前方一段道路. 如果这段道路中存在n个预瞄点，与每一预瞄点处匹配的预瞄时间为tl～tn，跟随误差为el～en. 随着车辆的移动，这些预瞄点的信息也在不断更新，驾驶员由此进行行驶决策，从而模型具有类似于模型预测控制的滚动更新的特点. 为使每一预瞄点的跟随误差值最小，则有

(1)

综合考虑全段预瞄轨迹的跟随误差值最小，建立二次型指标函数，则有

(2)

以上为以单一跟随误差最小目标的多点预瞄驾驶员模型，而因驾驶员的驾驶风格不同(或行驶条件不同)，为了稳定车身或驾乘感受舒适，在一定程度上放弃跟随误差最小指标，以换取较小的侧向加速度. 加速度最小指标可以描述为

(3)

综合式(1)与式(3)，便可将多点预瞄模型发展为多点双目标决策模型. 在预瞄点i处，分别以权系数p和q，表征驾驶员对跟随误差及侧向加速度的决策意愿，建立指标函数

(4)

综合以上指标函数，设每一预瞄点处的权系数为wi，则有

(5)

(6)

由于车速一定的情况下，Ti越大，预瞄距离越远. 所以，当m>0时，视野远处轨迹信息权重高；当m<0时，视野近处轨迹信息权重高；当m=0时,wi(Ti)=1,轨迹没一点的权重相同. 同时，|m|越大，相邻两个预瞄点的权重差距的越大，t1～tn预瞄区间内的远近重视区别越明显. 通常取值范围在m∈[0,5]即可表现出驾驶员较丰富的视野特征.

2 驾驶员决策精度差异建模

上文提到的侧向加速度决策，是基于最优理论得到. 但真实的驾驶员不会像计算机一样，在每一次决策时都能够计算出侧向加速度的最优值. 更贴近现实的应是驾驶员每次决策的加速度值都在最优值周围的一定范围，并且这一范围应有一定规律可循. 文献[6]中，将驾驶员对轮胎真实侧偏角的估计考虑为一种高斯函数的分布行为，同样在这里，假设驾驶员的决策行为符合一定的高斯分布，从这一角度描述不同决策精度的驾驶员.

(7)

(8)

令：

(9)

由式(8)和式(9)得

(10)

(11)

3 驾驶风格与驾驶员能力

以上的理论建模阶段，可以看到表征驾驶员特征的参数在原有预瞄时间tp，神经反应滞后时间td，以及肌肉操作滞后时间th的基础上，发展为更丰富和贴近真实驾驶员的视野特征、决策取舍特征及决策精度特征的描述方式. 由4个自由参数表示这些特征，如表1和表2所示.

表1 表征驾驶风格及能力的物理量及意义

这里提出了驾驶风格和驾驶员能力两个相互独立又可以交叉的概念. 驾驶风格，表现驾驶员对车辆驾驶方式的取向，属于驾驶员的意愿：一种为对远近轨迹信息的取舍;另一种为对跟随精度和乘坐感受的取舍，与驾驶员本身能力无关. 因为驾驶员能力是驾驶员对驾驶方式决策的最优侧向加速度的实现能力，成熟驾驶员的决策相对更容易接近最优值，生疏驾驶员决策相对更不易接近最优值. 驾驶风格和驾驶员能力的概念互不影响，可以自由匹配.

4 仿真验证

在Matlab R2013a/Simulink和Carsim 8.1建立联合仿真平台，以双移线工况进行仿真验证，主要从预瞄区间大小、视野窗函数选择、跟随误差侧向加速双指标权重值以及驾驶员决策精度系数4个方面进行仿真对比.

针对视野区间的仿真如图1所示. 车速为80 km/h，视野窗函数为wi=1，即视野区间内所有预瞄点权重相同，预瞄点个数n=10，不考虑侧向加速度指标以跟随误差最小为单一目标，并忽略决策偏差，分别在视野区间[t1,1,t1,10]=[0,0.6 s]和[t2,1,t2,10]=[0,1.0 s]进行仿真对比. 在图1中，两种预瞄方式下，驾驶员转向操作的起始位置分别为X1=46.69 m，X2=37.82 m. 由于此处所述“预瞄视野”为驾驶员决策的依据，所以预瞄视野越长，就越能够提前获取道路信息，并进行操作决策.

图1 驾驶员视野区间大小对轨迹跟随的影响Fig.1 Effect of driver's visual field for path tracking

图2 驾驶员视野窗函数对轨迹跟随的影响Fig.2 Effect of horizon-window for path tracking

针对驾驶员决策取向的仿真结果如图3、图4所示. 其中跟随误差权重参数为p，侧向加速度权重参数为q，车速设定为60 km/h，视野区间[t1,1,t1,10]=[0.3,0.6] s，视野窗函数为wi=1，最大跟随误差和最大侧向加速度如表2所示.

图3 驾驶员决策取向对轨迹跟随的影响Fig.3 Effect of decision intention for path tracking

图4 驾驶员决策取向对侧向加速度的影响Fig.4 Effect of decision intention for lateral acceleration

表2 决策取向参数对跟随误差和侧向加速度的影响

可以看到，决策取向参数p/q对跟随误差和侧向加速度大小的影响明显，与理论相符.p/q的值越大，说明驾驶员模型所模拟的驾驶员对跟随精度要求的越高，偏向于驾驶的精准性；p/q的值越小，说明所模拟的驾驶员希望侧向加速度最大值越小，偏向于驾驶的舒适性.

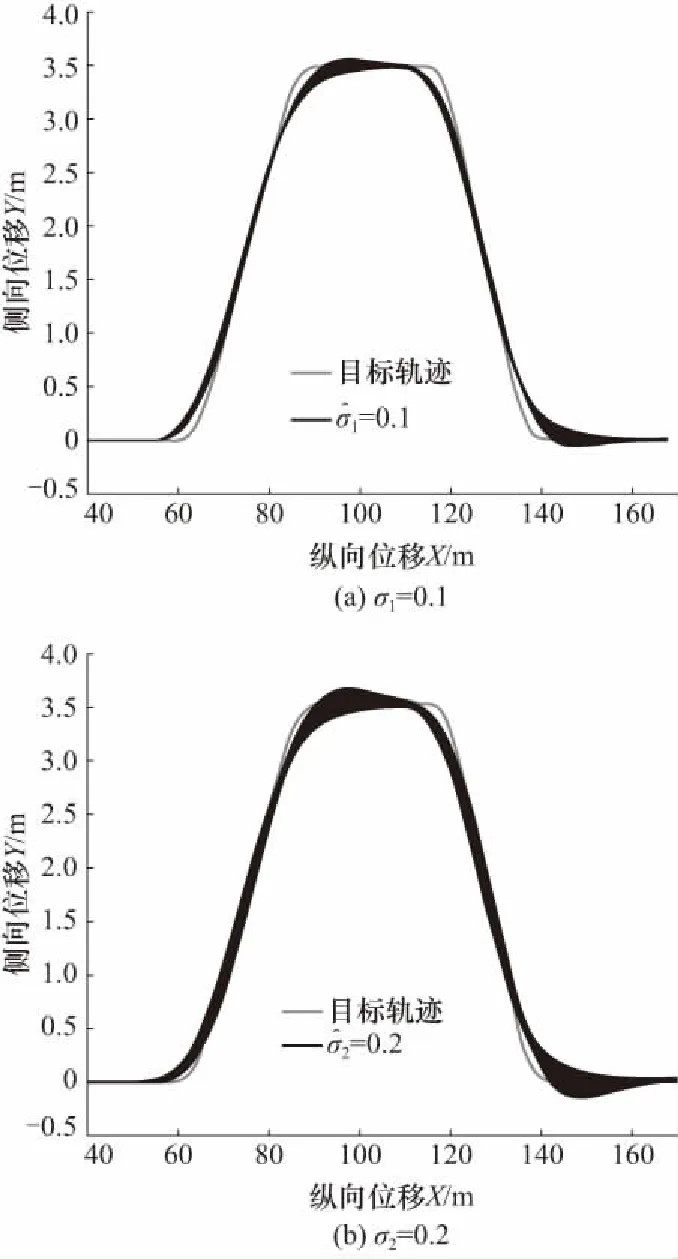
图5 决策能力对轨迹跟随的影响Fig.5 Effect of driver's decision ability for path tracking

5 结 论

以驾驶员决策行为及侧向物理模型为基础，建立以侧向加速度与方向盘转角的稳态增益Gay为经验的，以驾驶员视野为单位的滚动寻优车辆转向操作算法，内部自由参数能够表征驾驶风格及驾驶员能力.

区分了驾驶风格和驾驶员能力的概念. 以视野特征，决策意愿特征表征驾驶风格，代表驾驶员的决策意愿；以决策精度特征表征驾驶员能力，代表驾驶员对最优决策的实现能力. 两个概念彼此独立，可相互匹配.

视野特征以参数[t1,tn]表征驾驶员的视野范围大小，以视野窗函数wi=tim表征远近重视取向；决策意愿特征以权值比p/q表征驾驶员对跟随误差和侧向加速度的取向；决策精度差异特征以方差参数σ表征真实决策值与最优决策值的差距程度. 4组自由参数的相互匹配，拓宽了驾驶员模型的模拟范围.