启发思维落实核心素养的几个切入点——以一节高三习题课为例

浙江省镇海中学 (邮编：315200)

2017年版的《普通高中课程标准》指出：“在教学过程中，要始终体现学生的主体地位，教师应充分发挥学生在学习过程中的主动性和积极性，激发学生的学习兴趣，营造宽松、和谐的学习气氛[1]……” 在高三复习课教学中，如何发挥学生的主动性和积极性？高三课堂教学内容多、容量大、难度高，如何找准学生的“兴奋点”？笔者认为只有找准思维的启发点，逐步切入，努力培养学生的主体意识，体现学生的主体地位，激发学生的学习自主性、能动性、创造性，从而在问题解决的过程中逐步落实数学核心素养．下面结合高三习题课一道二元最值问题的求解过程，具体谈谈启发思维落实核心素养的几个切入点：

1 疑难之时点拨

启发思维一个重要的时机就是在学生解决问题的过程中，尤其是在解决过程中遇到阻力之时．疑难之时点拨就是在学生找不到前进的方向时，教师应该适时地发挥“引路人”的作用.

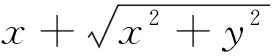
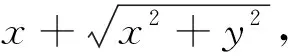
2 点拨之后反思

点拨学生之后，引导学生抓住主要矛盾，从不同的视角、不同的维度、不同的高度，带领学生重新剖析题目条件，重新认识遇到的数学问题，从而抓住解题核心，找准解题的方向.

本题中，结合题目特点不难得出：视角一，从代数的角度看：可以看成方程；可以消元；可以选择换元……视角二，从几何的角度看：可以看成直线和距离；可以看成向量的模……在具体的分析过程中，应该抓住某一个点来启发思维，经过逻辑推理，逐步落实这些想法一一解答.

视角一代数角度

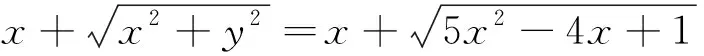
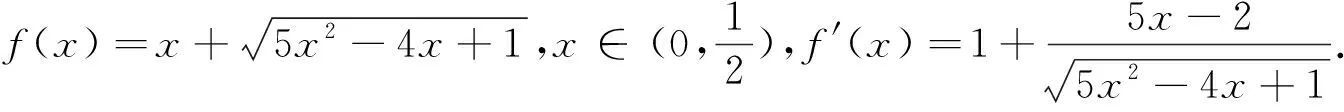
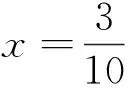
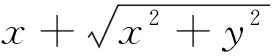
视角二几何角度

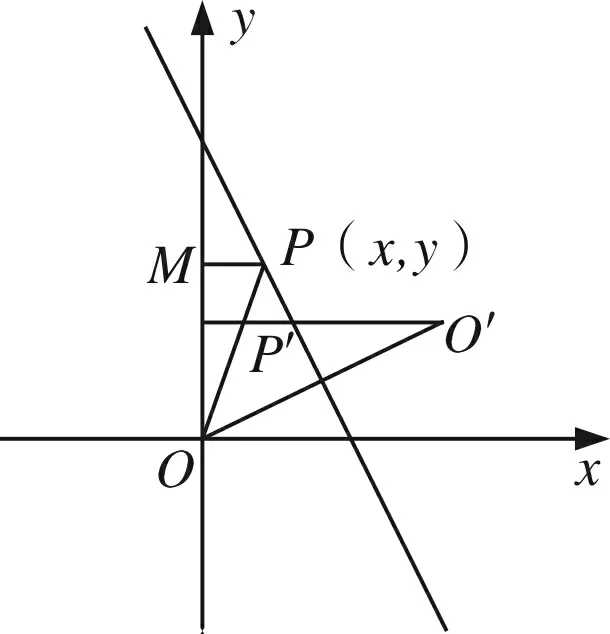
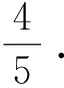
在学生突破题目难点，找到一种解法后，趁热打铁地引导学生进行题后反思，思变、思同、思异、思源，对问题本质的重新剖析，反思解题方法、解题技巧、解答过程，力求一题多解，一题多变，将思维由特殊推向一般，使问题层层深入，寻找总结通性通法，使思维逐渐深化.

本题中，我们已经从代数几何两个角度较圆满地解决了这个问题.但是，从思维的角度，站在更高的层次，我们不仅要问，仅此一种消元方法吗？

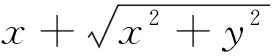
启发思维点四：从变量主次关系上，看成含有一个变量的方程，用判别式法.

3 反思之机发散

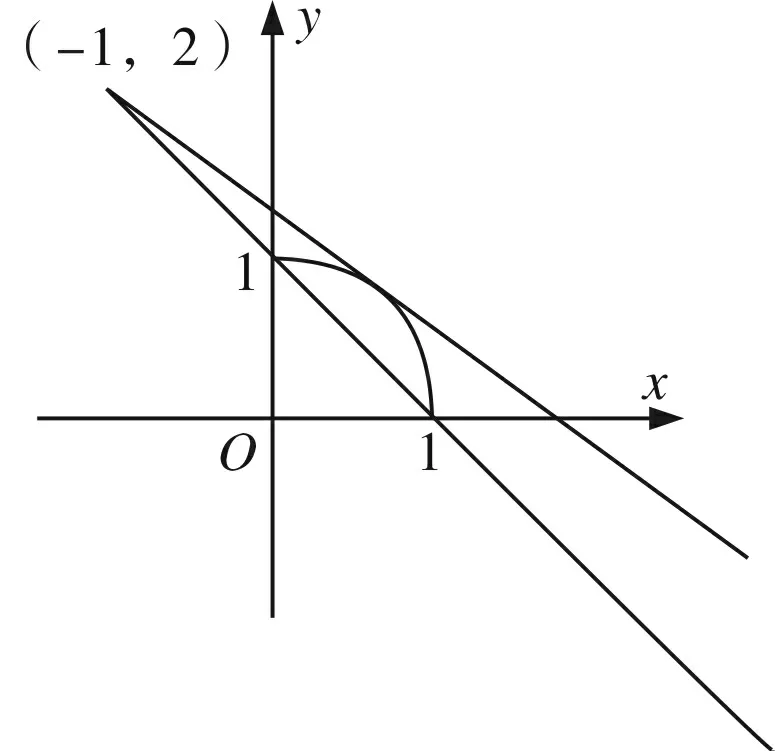
文[2]中指出，题后小结是一种自我提升的重要手段．思变，拓宽题目背景、发散思维是基础；思同，思考结论属性、总结归纳是切入点；思异，猜想性质范围、大胆推广是关键； 思源，追溯事物本质、掌握客观规律是核心．本例中，以上已经多角度解决了此问题，但是我们不禁要问，能不能借助转化与化归的思想方法，将其转化为我们熟悉的特殊的模型？

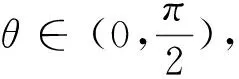
方法一：(利用三角函数的有界性)整理得：(2m-1)cosθ+msinθ=1，即

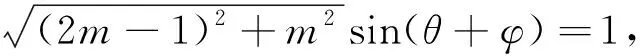
4 发散之后小结

通过前面几步的反思发散，带领学生重新认识我们所学内容，从思维的角度、思维的过程、思维的结果等方面进一步增强学生解题体验，加深对知识的理解．发散是为了聚焦，通过发散思维，拓展解法，最终在发散的过程中，总结提炼为什么这样解？为什么能这样解？怎样解才是最好等方法.

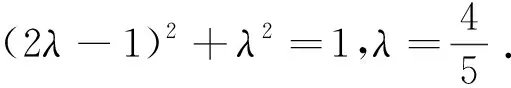
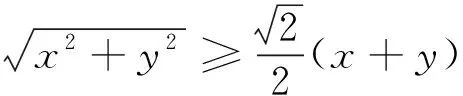
至此，这种解法从反面、从代数上解释了为什么所求为最小值，结合刚刚视角二启发思维点二解释了为什么有最小值．从而圆满地解决了此问题．不仅如此，还给我们以后解决此类型的问题，提供了方法上的借鉴.

5 小结之处升华

课后，可以让学生在解题后反思的基础上，要求学生在思考的基础上理解：二元(多元)最值问题，一是“减元”(或减参)，化为单变量问题；减元方法有很多，可以采用消去法、齐次化、判别式法.二是“换元”，具体包括三角换元、齐次代换等．换为熟悉的形式、换为熟悉的模型．三是数形结合法．在数学问题的解决过程中，紧紧把握数与形的特征，可以从代数和几何两种角度来认识所求问题，可以方便地找到解决的方向．更要在求解二元最值的过程中，体会运用了哪些思想方法？碰到了哪些困难？有何感触？这样的总结，可以升华为对所学知识的深层次的理解，久而久之，这种理解就会慢慢转化为学生一种能力，一种素养.

近几年的高考题，背景新颖、能力要求高、内在联系密切、思维方法灵活，充分体现了课程标准理念，这就使得我们在平时的教学过程中，不能仅仅停留在题目的解决上．更应该从题目的解答上升为对知识深层次的理解，即更加注重知识的形成过程，更加关注学生获取知识的过程，更加关注学生思维能力发展的过程，从而培养学生创新精神和实践能力.