相容拉格朗日-欧拉法求解黏性流体中弹性圆柱壳的振动

郝亚娟， 郭茜茜， 陈佳慧

(燕山大学 理学院， 河北 秦皇岛 066004)

近年来，在海洋资源开发利用等方面的需求驱动下，许多科研人员着眼于研究水下生物的运动机理，指导水下机器人[1]的研究，所以仿生学[2]的研究具有了广阔的应用前景和巨大潜在价值，涉及到流体力学、机械、材料、控制、生物等学科。

根据Lighthill[3]对水中生物运动方式的分类，波状摆动推进是其中的一种，该推进方式生物身体做横向扭曲、往复摆动，以横波的方式由前向后或逆向传播。早在20世纪50年代，Taylor[4]采用“静态流体理论”分析计算微生物运动的流体力，该方法忽略惯性力影响，适用于雷诺数比较低的情况。Lighthill[5]提出一种应用于变形体的“细长体理论”，该理论指出细长鱼类获得较高推进效率的条件。随后Wu[6]首先提出了“二维波动板理论”，该理论将鱼体看作一块弹性薄板，分析了二维柔性波动板的游动过程。Chopra等[7]又将“二维波动板理论”进行了扩展，提出了可用于大摆幅推进系统的理论。Triantafyllou[8]通过观测证实了二维和三维波动板理论的真实性。Tian等[9]用不可压缩的纳维-斯托克斯方程数值解来了解行波表面推进机制，用灵活的箔来模拟行波运动游泳体模型，分析向前推进速度和流场。

国内外学者对相关理论开展广泛的研究，取得了一些成果，但仍存在不足之处，对水中生物的推进机理还需进一步深入研究。本文尝试将水中生物看作弹性圆柱壳体，假设圆柱壳长度足够长并远远大于半径，将其近似为无限长。另外假设速度很小，雷诺数Re<0.1，属于低雷诺数流动，采用斯托克斯方程近似，这样运动学问题和动力学问题相互独立，因此速度与流体的黏性无关[10]。采用相容拉格朗日-欧拉法[11]求解无限长圆柱壳位于黏性流体中，当壳体表面发生行波振动，黏性流体的运动速度以及壳体的推进速度。相容拉格朗日-欧拉法的优势在于，壳体采用拉格朗日法描述，流体采用欧拉法描述，在接触面结合这两种方法，这样可直接利用流体力学和固体力学中的基本方程。相容拉格朗日-欧拉法求解弹性体理想流体绕流问题显示了方法的有效性[12-13]，本文尝试采用该方法研究黏性流体问题。

1 基本方程

对于不可渗透表面，应用黏性流体分子对表面的黏附条件和压力矢量平衡条件，可以将表面接触条件简化。“相容”黏附条件简化为

(1)

式中：u是弹性体固定点的位移矢量;V为与变形后弹性体重合的流体空间点处的速度矢量;t为时间。

在圆柱坐标系(r,θ,z)中，变形后空间点处沿单位矢量kl(l=r,θ,z)方向的速度矢量分量近似值Vl(l=r,θ,z)用变形前空间点处速度矢量和位移矢量沿坐标轴方向的分量vl和ul(l=r,θ,z)的泰勒级数展开式近似表示

(2)

由于壳的位移分量太小，故泰勒级数展开式的第三项不予考虑。

由式(1)得接触面的运动条件为

(3)

Vz、Vθ和Vr的值可由式(2)计算得到。

对于不可压缩黏性流体的纳维-斯托克斯方程，在圆柱坐标系中形式如下[14]

(4)

其中

式中：μ表示流体动力黏性系数；ρ表示黏性流体质量密度，p为单位质量流体压力；Fr、Fθ和Fz表示单位质量的质量力在三个坐标轴的投影。

假设流体速度很小，雷诺数Re< 0.1，式(4)左边的惯性力同式(4)右边的第三项黏性力相比可以忽略，而且运动是定常的，质量力可以略去，则与θ无关的二维流体运动的纳维-斯托克方程简化为斯托克斯方程[15]

(5)

其中

相应的连续方程为

(6)

2 问题的解

圆柱壳体表面行波振动形式如下

(7)

式中：α=2π/λ，ω=cα，λ和c为波的长度及速度，Zn和Rn为振幅。

引入流函数ψ满足

rvz=∂ψ/∂r，rvr=-∂ψ/∂z

(8)

式(8)满足连续方程式(6)。

由式(2)、式(3)和式(8)，接触面运动方程式(3)可以写成如下形式

(9)

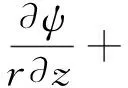
(10)

式(5)中消去压力p得到如下方程

(11)

方程式(11)具有如下形式的解

BnrK1(nαr)]sinn(αz-ωt)

(12)

该解满足条件

vz=V0(r→∞)

式中：V0是与时间无关、相对于不动坐标系无穷远处流体的运动速度，由给定问题及系数An和Bn同时确定，K0(x)，K1(x)是麦克唐纳函数[16]。也就是说，相对于无穷远处不动的流体而言，壳的推进速度等于-V0。

将式(7)和式(12)代入式(9)和式(10)，并利用如下关系式[16]

(13)

可得

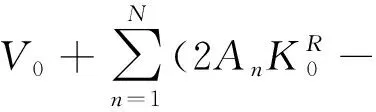
(14)

(15)

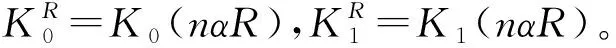
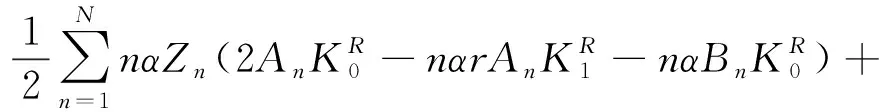
(16)

由式(14)和式(15)得

(17)

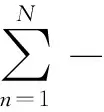
(18)

由式(16) 、式(17)和式(18)可得

(19)

(20)

其中

(21)

由式(16)、式(19)和式(20)得速度V0

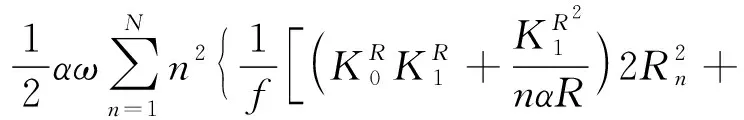
(22)

流体的速度vz和vr分别为

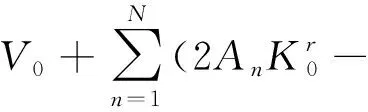
(23)

(24)

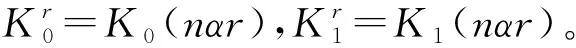
当nαR为大值时，利用函数渐进值

由式(22)，令圆柱壳的半径R→∞，可以得到薄板振动时的无穷远处流体速度V0为

(25)

3 结果分析

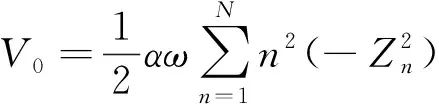
经编程分析可知，N取值不同，速度的具体数值不同，但变化规律一致，振幅和频率对于速度的影响是显著的，随着振幅和频率的增加，速度增加，而波长的变化对速度的增加几乎没有影响，该结果与文献[11]一致。以下取N=1计算。

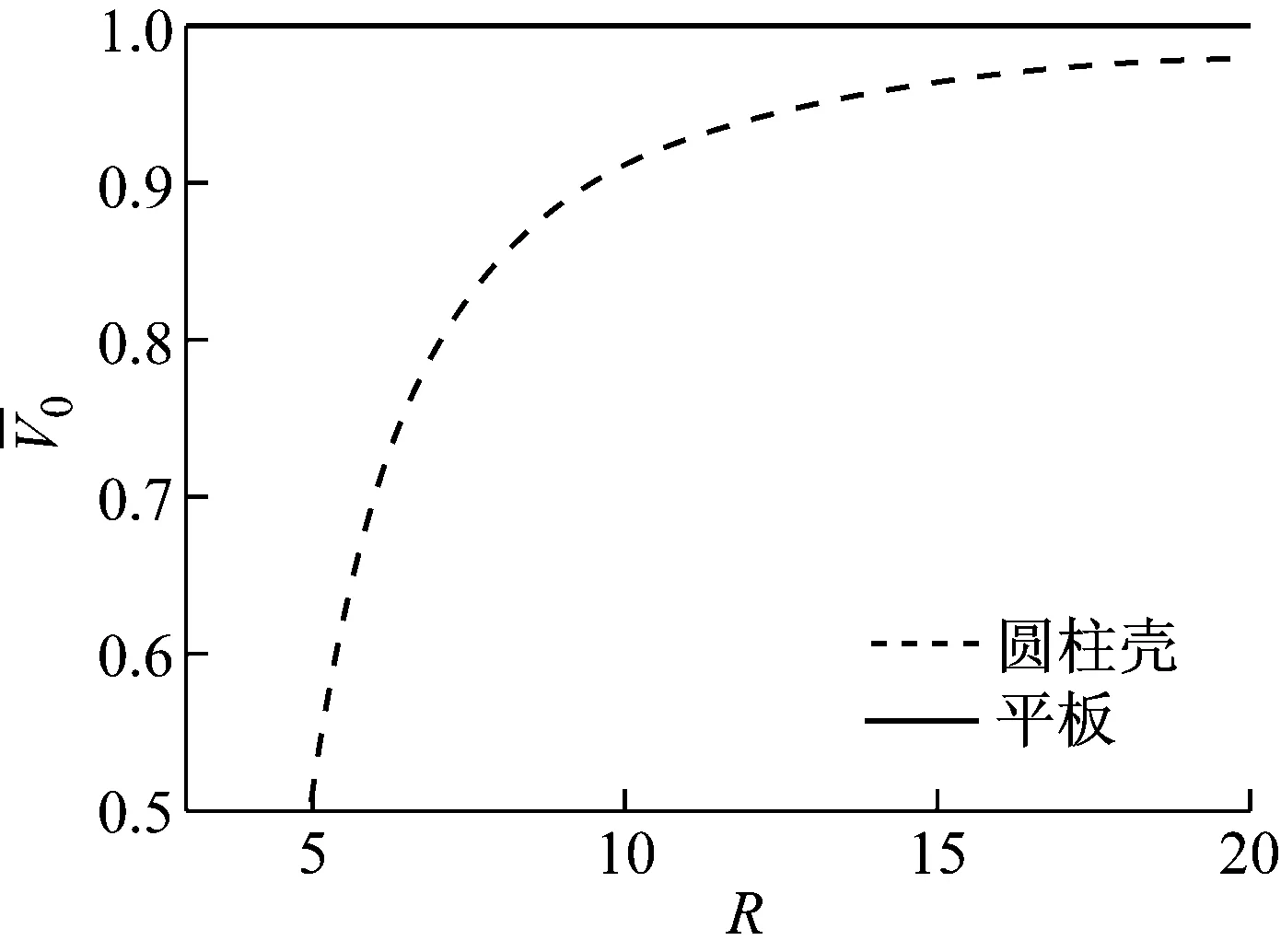
图1 随R增大圆柱壳与薄板值比较

对于弹性薄板，取N=1，表1给出了Z1和R1不同取值时V0/c的数值。从表1可以知道，纯横向振动(Z1=0，R1≠0)时无穷远处流体的运动速度与波的方向相同，而纯纵向振动(Z1≠0，R1=0)时二者方向相反，即纯横向振动时薄板的位移和波的方向相反，纯纵向振动时二者方向相同。若两种振动均有，由式(25)可知，当R1的数值位于-2.4Z1与0.4Z1之间时，无穷远处流体的运动速度与波的方向相反，否则方向相同。

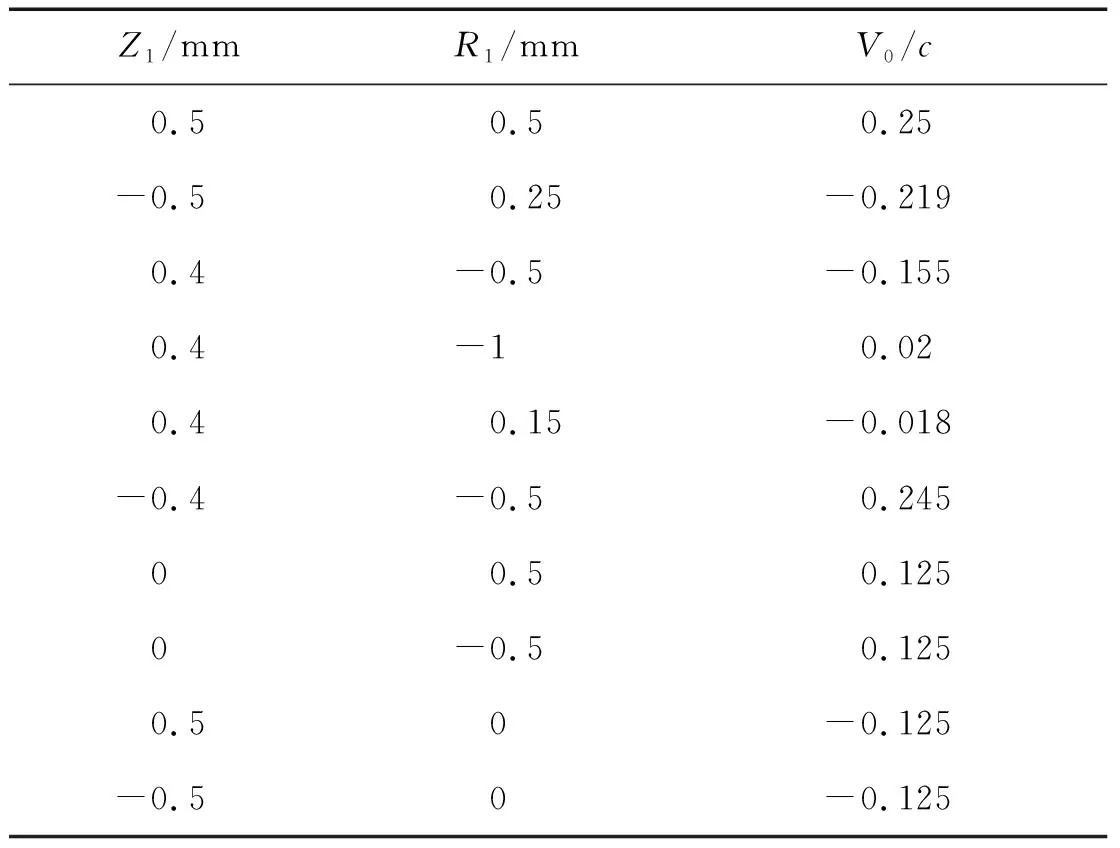
表1 对于薄板Z1和R1不同取值时的V0/c数值

表2 r=1.5R处和的最大值

4 结 论

(1) 接触面条件中变形后的速度分量用变形前分量的泰勒级数展开式近似表示，简单明了，适用性强；

表3 不同位置处的最大值

(2) 横向振动对于黏性流体速度的影响是主要因素，纵向振动对结果影响很小；

(3) 圆柱壳表面做纯纵向振动时，与时间无关的无穷远处流体的运动速度与圆柱壳半径无关；

(4) 弹性圆柱壳半径较大(薄板)做纯横向振动时壳的位移方向与波的方向相反，纯纵向振动时二者方向相同，两种形式的振动均有，则方向可能相同，也可能相反。