激波管管长对阶跃压力波形的影响分析

杨 军， 薛 斌

(1. 北京长城计量测试技术研究所， 北京 100095； 2. 北京航空航天大学 仪器与光电工程学院， 北京 100191)

激波管作为阶跃压力发生装置已经有一定的研究历史，因其可以实现较为理想的阶跃压力，在化学动力学、气体动力学、燃烧以及爆炸工程研究等方面都得到了广泛的应用。在航空领域内，随着对发动机喘振等现象地不断研究，有关动压的研究近些年也得到很大程度的发展。作为计量校准的一项重要发生装置，激波管的高低压段长度，管内膜片破碎情况，管腔内选择的气体介质属性，腔室间膜片的材质以及厚度选择等都会对产生的阶跃压力以及压力平台时间造成影响。

近些年国内外对于激波管的设计研究都取得了很大程度的突破。在提高激波管阶跃压力幅值域度的研究方案中，范毓润等[1]将管腔内的气体介质换成H2和CO2，通过理论分析和实验验证了通过CO2驱动H2可以一定程度上提高压力增益。葛竹等[2]通过比较四种不同气体作为压力源，得出通过介质的调整可以改变压力幅值域度。黄芬[3]采用基于预压力的水激波管校准方案，将阶跃压力的幅值提高到了700 MPa,频带达到了1 kHz。Larergue等[4]带队研制出的50～60 MPa的高动压标定激波管为建立动压标准奠定了基础。薛莉[5]利用双膜片的破膜方式，更大程度上提升了阶跃压力幅值。在阶跃压力下限的研究当中，杨军等[6]采用双腔负压法扩大了阶跃压力的域度。

对于针对激波在传递过程中边界层的影响问题，全鹏程等[7]通过实验的方法研究了激波与层流边界层的相互作用。由于激波管形成的阶跃压力的平台时间用于压力传感器的标定，因此尽可能延长阶跃平台时间可以获取更为丰富的压力源低频分量。针对此研究，袁俊先等[8]通过理论分析以及实验，验证了在其他条件不变时，通过增加激波管高压腔长度可以一定程度上增加平台时间。

1 压力激波管工作原理

1.1 理想状况下激波理论

在理想的状况下，即不考虑激波管内壁的黏性以及与管壁之间的热传导等因素，在膜片破碎前后，整个管腔内的压力分布变化过程，如图1所示。

(a) 激波管初始压力

(b) 激波管膜片刚破碎时状态

(c) 稀疏波反射状态

(d) 激波到达端面反射时状态

图1中P1和P4分别为破膜前高压段和低压段的初始压力，P2为膜片破碎后激波进入低压段时产生的压力，P5为激波到达低压腔底端面后形成的反射压力。基于激波理论可以推导出激波管内压力随时间变化情况[9-11]。

当入射激波运动到底端面位置时，会在固定壁面上发射现象，为了满足固定壁面附近不能出现真空状态这一边界条件，会形成反向传递的激波。入射激波的波前到达端面并反射的过程时间极短，通常在几十ns级别[12]。

基于得到的激波马赫数，P2和P5与低压室压力的关系为[13]：

(1)

(2)

从理论分析上可以看出，在理想情况下阶跃压力的大小只与初始状态的压力介质与膜压比有关，与激波管自身的长度并无关系。

1.2 阶跃平台时间

在激波发生反射后，波后为压缩区域，为了满足边界条件，波后区域内的气体流动为0，此时即会形成阶跃压力平台。当反射激波先传递到接触面时，会在接触面上发生二次反射，新形成的反射激波运动到底端面时，平台被破坏，平台时间结束。当反射稀疏波先于接触面到达底端面时，同样会导致平台被破坏。为满足动态压力的校准需求，通常要使得阶跃平台时间尽可能长。在这样的情况下，当反射稀疏波、接触面、反射激波三者交汇于一点时，产生的阶跃压力平台时间最长，此时三者的运动轨迹，如图2所示。

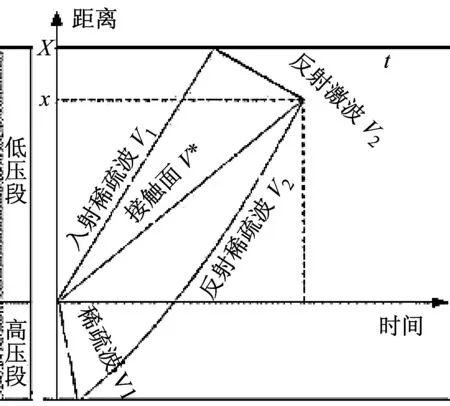
图2 激波管阶跃平台时间最长情况下速度变化情况

根据激波管内气体在传递过程中的状态参数关系以及量热气体状态方程，当高低压腔介质选择为空气时，接触面的传播速度v*与激波速度V1之间关系如下[14]：

(3)

激波抵达底端面后反射的激波速度为V2，与正向传播的激波速度关系如下：

(4)

不妨假设反射激波，接触面以及反射稀疏波交汇点的位置为x，低压室的长度为X，高压室长度为单位长度，若激波与接触面到达x的时间差为t，则有：

(5)

(6)

根据激波管气体流动特征关系，接触面运动的马赫数M与激波速度存在如下关系：

(7)

可以推导得到x与M之间为：

x=2M(1+M/5)2

(8)

因此最优的激波管高低压段长度比与破膜之后激波的马赫数Ma之间的关系为：

(9)

根据上述理论，可知破膜前高低压腔压力值影响产生的激波马赫数，而不同马赫数对应不同的管腔最佳设计尺寸。

2 激波管仿真分析

为了和实验数据相比较，同时分析激波管长度的影响因素，本文建立两种不同模型尺寸。第一种为高压段长度为2 m，低压段长度为9 m；第二种高压段长度为4 m，低压段长度为7 m，且管腔直径均为0.1 m。基于上述两种激波管尺寸进行仿真模拟。

2.1 仿真模型建立

考虑黏性因素时，激波管初始膜压比以及介质决定了破膜瞬间产生的压力幅值以及激波大小，而管腔长度则与激波传递过程造成的衰减程度有关，同时影响了平台时间的长短，因此在管腔长度已知时，可以对高低压腔长度进行优化，从而得到更加理想的阶跃幅值以及平台时间。

在边界层方面，Kevin等[15]通过实验和仿真的方式研究了边界层对激波的阻滞影响。本文仿真分析采用应用于流体分析的FLUENT软件，分别选用无黏模型以及Renormalization-group(RNG)k-e模型进行研究。认为气体介质在高低压腔内满足理想气体方程，边界层位置选择小尺寸网格使计算更加准确。膜片因为厚度尺寸相对于管腔整体长度很小，因此膜片位置的网格进行细化。膜片在真实实验中难以实现理想破碎，但是瞬间形成的激波大小不受破碎状况影响，且在传播过程中，激波会进行自身调整，低压腔足够长时激波到达底端面时近似为平面波。根据激波管自身的轴对称性，建立二维模型进行分析研究，可以有效缩短计算周期。

在网格划分方面，考虑边界层的黏性因素影响，采用三角形单元可以提高边界位置处的计算精度，同时进行网格细化，边界位置以及高低压腔连接处进行特别细化，保证网格质量超过80%，至仿真结果不发生数值偏差为止。

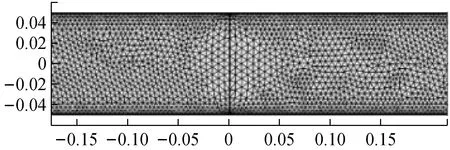
图3 激波管膜片附近网格划分

在求解过程当中，采用的RNGk-e模型方程中湍流动能k以及湍流耗散率e方程，并在边界条件设置上，不考虑管腔内部与外部的热交换，因此壁面设置为wall，且初始状态下定义整个管腔压力为大气压，通过region进行区域选择，将高压腔范围内采用patch更换为对应初始高压。因为实际激波上升沿时间较短，实验中通过压力传感器测量的上升时间为ns级，因此courant number定义为2加快收敛，迭代步长选择为1 ns。

2.2 无黏情况下平台时间

为与实验相互验证，本文低压腔的初始压力均为标准大气压0.101 MPa,高压腔的3组不同初始条件的情况分别为3倍大气压，10倍大气压以及20倍大气压。且3组仿真的温度条件都认为是在常温300 K下进行的,通过计算可知此时音速为347 m/s。激波管膜片破碎前后，整个管腔内的压力分布变化过程，如图4所示。

(a) 膜片破碎前初始压力分布(b) 膜片破碎后压力分布

(c) 稀疏波反射后压力分布(d) 激波反射后压力分布

图4 FLUENT仿真激波管破膜前后不同位置压力变化

Fig.4 Pressure change process during the shock tube diaphragm rupture at the different positions in FLUENT

从仿真结果的云图上可以看出激波管内压力变化情况与理论过程相同。在不考虑黏性条件时，利用方程(12)可以得到在已知初始高低压时，平台时间最长的设计发方案。且为和实验数据相比较，仿真设计尺寸均为总长11 m。

当低压室采用标准大气压，对高压室进行充压到3个大气压时，形成的激波马赫数为1.273，计算可得到此时高低压段最佳长度为2.6 m∶8.4 m，此时三种情况下在底端面位置所产生的阶跃压力为0.288 MPa。设计的两种尺寸与最佳理论长度比之间所产生的阶跃平台时间区别，如表1所示。

表1 当低压室为大气压，膜压比为3时仿真值

当高压室的初始压力为10倍大气压时，此时马赫数为1.607，同时得到此时高低压段最佳长度为1.5 m∶9.5 m，阶跃压力幅值为0.707 MPa,三种设计尺寸在阶跃平台时间上的差别如表2所示。

表2 当低压室为大气压，膜压比为10时仿真值

当高压室进行充压到20个大气压时，此时激波马赫数较高，接触面的运动速度超过音速，激波马赫数达到1.827，根据高低压最佳长度计算，可以得到此时最佳长度设计是1.0 m∶10.0 m，阶跃压力幅值为1.12 MPa,三种不同设计尺寸的平台时间差别如表3所示。

表3 当低压室为大气压，膜压比为20时仿真值

从仿真结果来看，在不考虑管壁的黏性因素时，膜压比对应唯一激波马赫数，同时可以看出最长阶跃平台时间随马赫数变化。在低压腔的初始压力为大气压时，随着马赫数增加，总管长一定，平台时间会减小。将仿真结果与理论计算相比较，可以看出由于网格细分以及计算步长等因素会造成一定误差，但结果趋势相吻合。

2.3 黏性衰减仿真结果

由于管壁内侧黏性因素作用，会导致激波在传播过程中出现衰减，因此马赫数也会随着传播距离的增加而降低。同时由于黏性因素影响，到达底端面处的压力小于刚刚破膜时产生的压力，因此激波管产生的阶跃压力要比理论值小。另一方面，由于激波在开始形成时因膜片破碎等原因会导致端面并不平整，在传播过程中会不断进行调整，在经过一段距离之后激波会形成较为平整的端面。

为此，分别对2 m∶9 m以及4 m∶7 m的两种管长比在不同膜压比下，距离底端面2 m内进行压力监测，根据压力出现变化时刻可以计算得到激波速度，即可以得到马赫数随距离的增加而逐渐减小的变化量，从而可以算出激波衰减系数，同时压力幅值会随着距离增加而降低。

对于2 m∶9 m的管长设计时，在距离底端面2 m距离内进行压力监测，选取3组不同初始膜压比进行仿真分析，其马赫数的衰减情况，如图5所示。

图5 2 m∶9 m时三种不同膜压比下，近底端2 m内的马赫数

对于4 m∶7 m的管长设计时，同样在距离底端面2 m距离内进行压力监测，选取同样的3组膜压比进行仿真分析，其马赫数衰减情况，如图6所示。

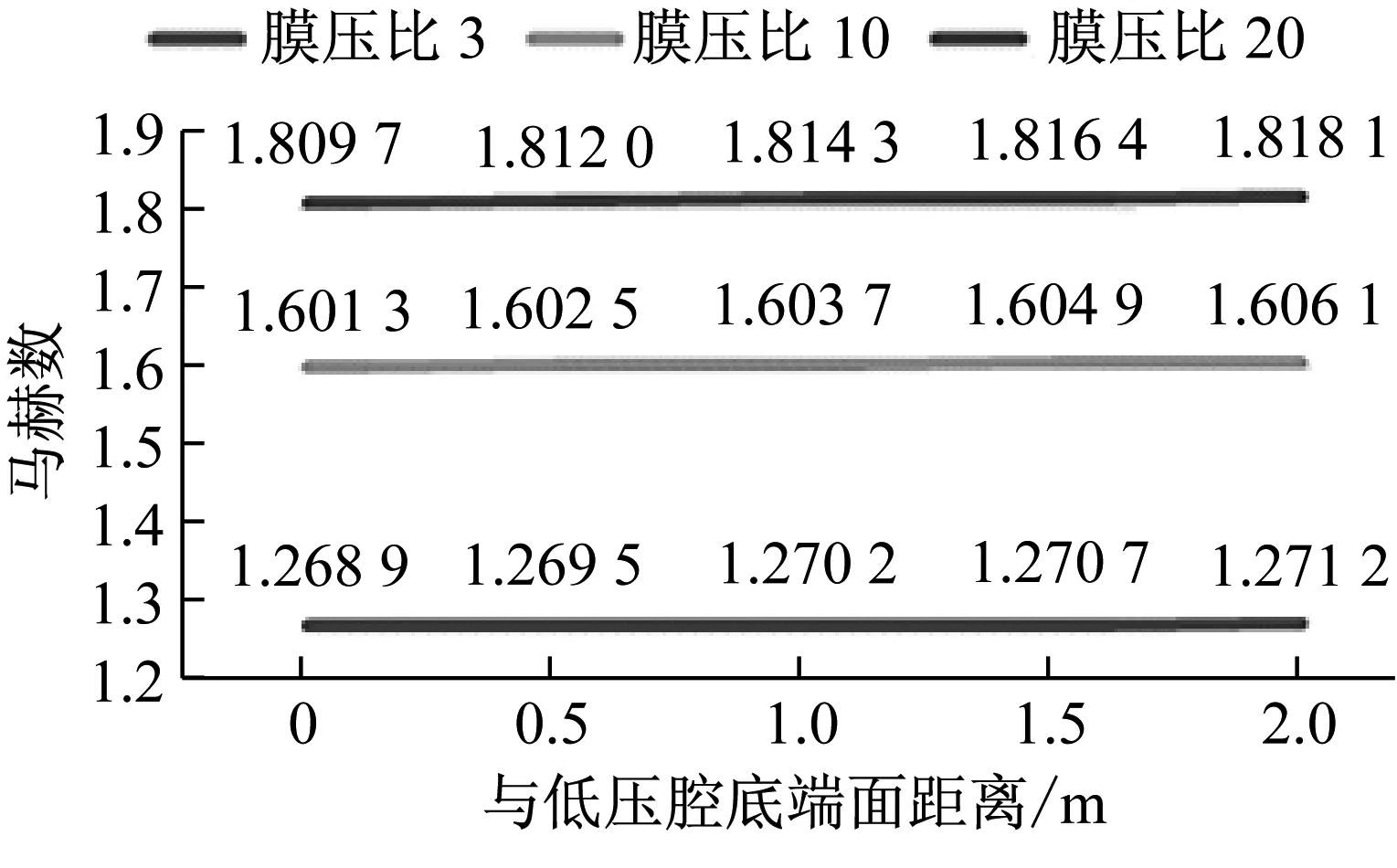
图6 4 m∶7 m时三种不同膜压比下，近底端2 m内的马赫数

针对两种不同管长设计，可以看出在近激波管底端面位置时，马赫数都随距离呈线性衰减，不妨定义马赫数衰减系数的表达式为：

(10)

式中：ΔMa表示单位距离内马赫数减小值，Ma则表示对应情况下，理论上膜片破碎后产生的入射马赫数的值。根据仿真结果，具体衰减系数结果，如表4所示。

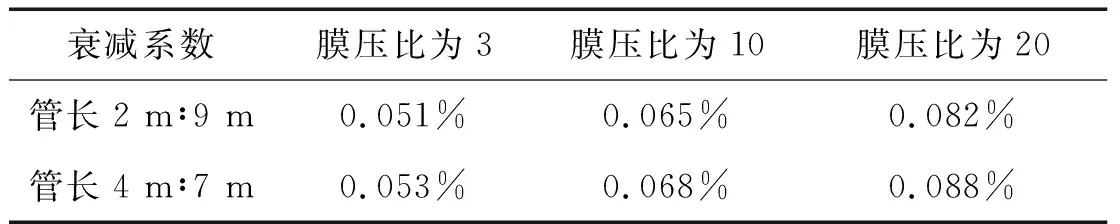
表4 不同状态下马赫数衰减系数

从衰减系数来看，在激波管选择的气体介质都为空气时，随着膜压比增加，马赫数在靠近底端面位置的衰减系数越大，且低压腔的尺寸较长时，激波此时趋于均匀，在底端位置衰减系数较小。由于黏性因素使得激波在传递过程中，产生的压力值也会随着距离增加而逐渐降低。在距离底端面2 m范围内压力幅值变化情况如表5所示。

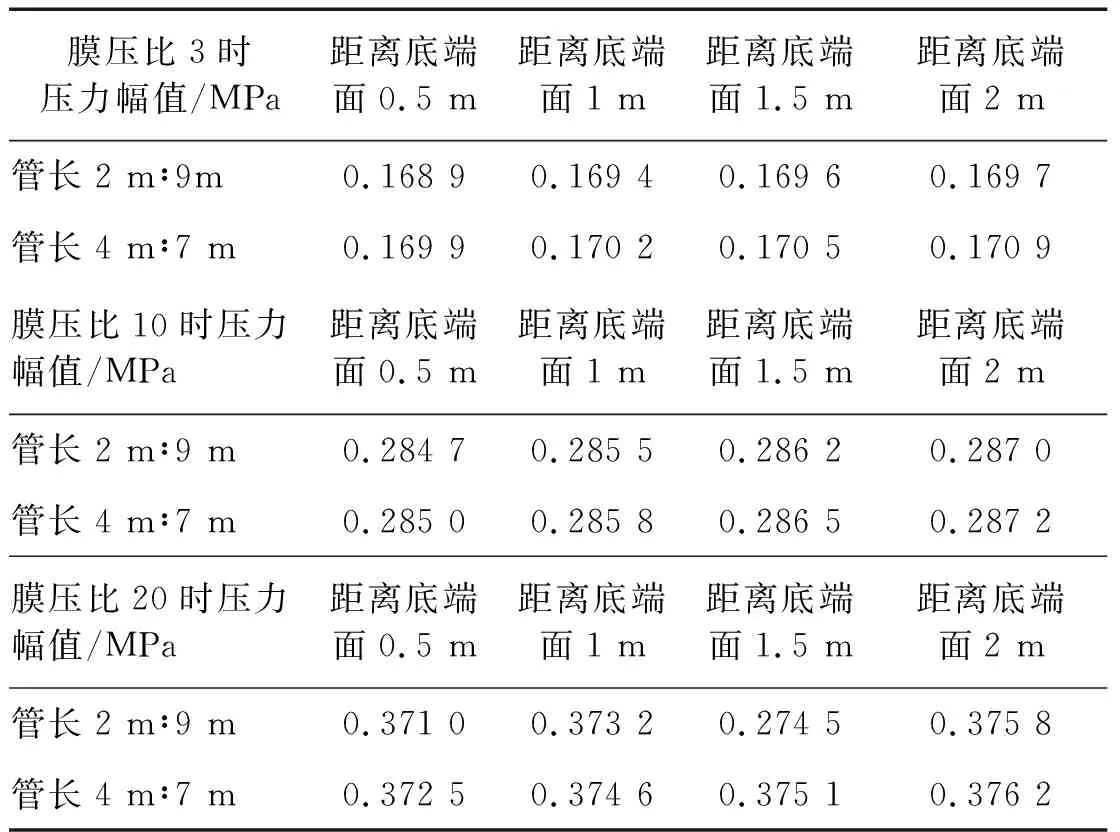
表5 不同初始条件时底端面位置附近的压力幅值

可以看出，激波在传递过程中，因受到管壁黏性因素的作用，导致的压力幅值随距离增加呈线性衰减，且衰减系数与管长设计长度，初始膜压比都有直接关系。同时，可根据获得的衰减系数对实验测量值进行修正。

3 激波管实验结果

目前由于实验中无法直接测量得到激波到达底端面时刻的具体马赫数，因此需要通过仿真的手段提供计算方案。实验在激波管近底端位置安装3个压力传感器，只能获取到激波来传递过程中，引发的压力阶跃的时刻，获取近底端两处马赫数值，且存在衰减现象,有必要对结果进行修正。

激波管的实验是在北京长城计量测试技术研究所的动压激波管上进行的。为进行长度分析，第一次采用高压室2 m，低压室9 m的方案进行试验，之后采用高压室4 m，低压室7m的方案进行设计，分析比较长度变化导致的阶跃压力大小和阶跃平台时间的变化情况。对于不同的实验情况选择不同的压力传感器以及放大器，不同的膜压比通过选用不同厚度的和不同材质的膜片进行控制。

在进行激波管的实验当中，采用ENDEVCO的8530C-15型号的传感器，以及选择CDV700型号的放大器。实验中在膜片选择方面，当低压室内为标准大气压的情况下，在膜压比较小时，使用0.07 mm的铝膜片，而在高膜压比的实验过程中，则采用0.3 mm以及1.8 mm厚的铝制膜片，且每次使用的数据采样点为100 000个。每组膜片实验进行10次，对三组阶跃压力幅值和平台时间进行归一化的方差分析验证重复性，根据方差的计算公式：

(11)

可以计算得到三组不同膜片的阶跃压力归一化的方差，如表6所示。

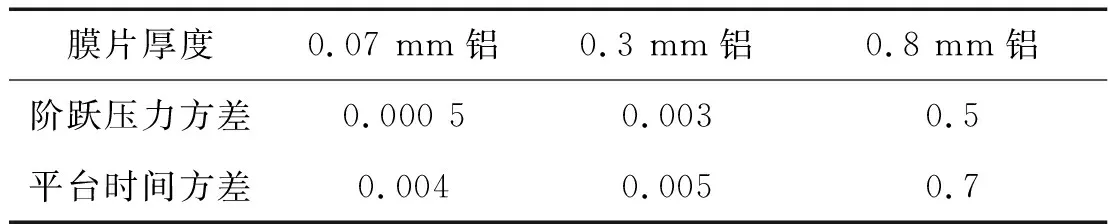
表6 不同膜片时阶跃压力和平台时间方差

可以看出阶跃压力的幅值和平台时间的方差均在实验误差允许的范围内。选用不同的膜片，即可以实现膜片破碎后产生不同的马赫数，从而产生的阶跃压力幅值以及平台时间也会有所区别，取实验数据的平均结果。在管长为2 m∶9 m的实验过程中，3组不同膜压比时底端面处压力值随时间的变化如图7所示。

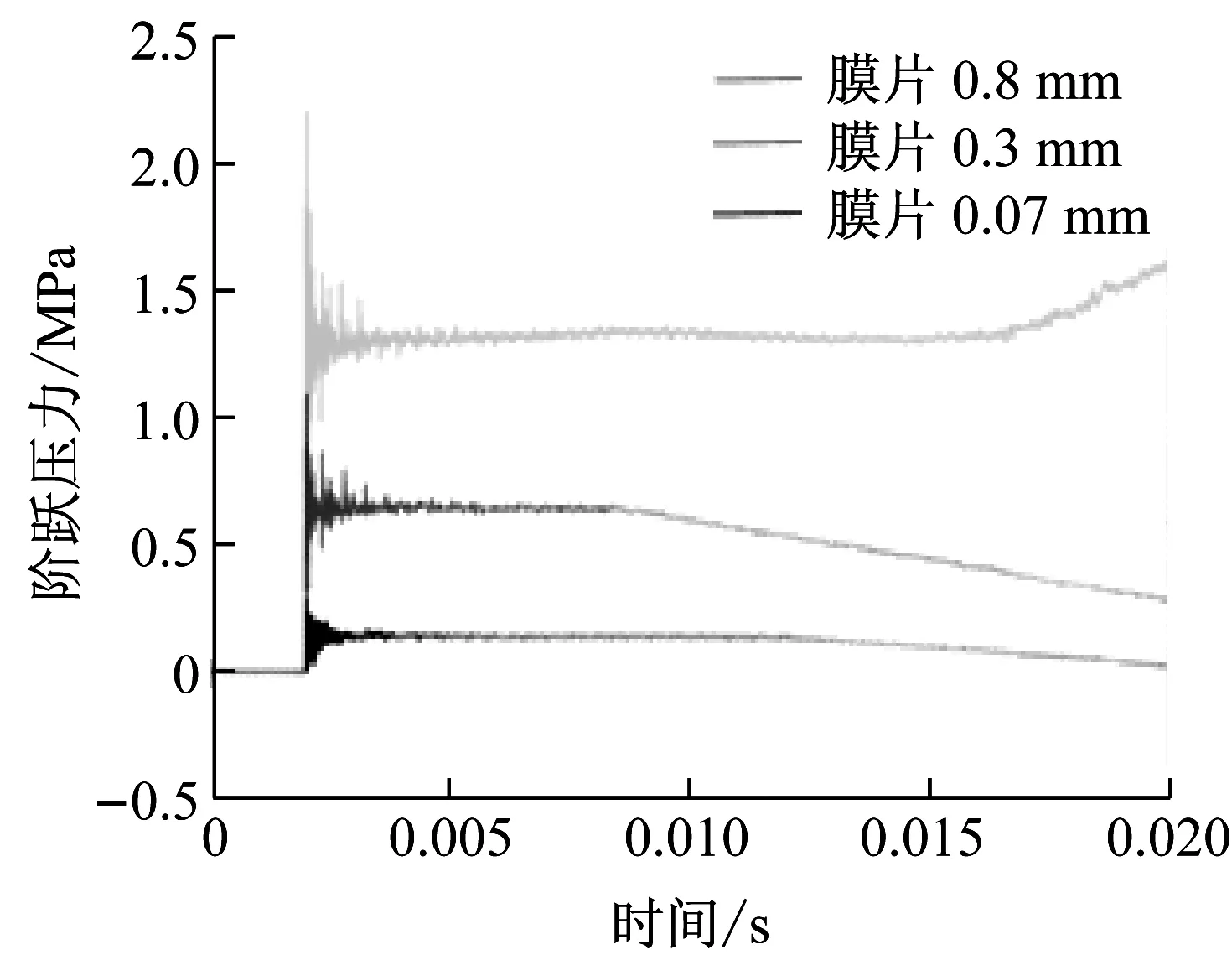
图7 2 m∶9 m时三种不同膜片时底端面压力变化

管长为4 m∶7 m的实验过程中，3组不同膜压比时时底端面处压力值随时间的变化，如图8所示。

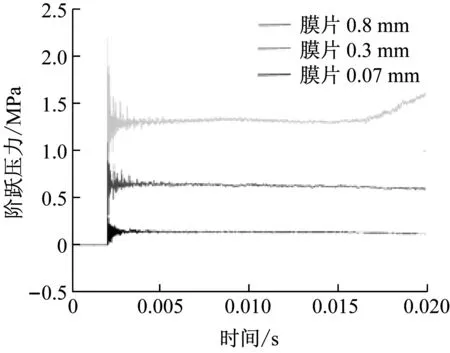
图8 4 m∶7 m时三种不同膜片时底端面压力变化

通过比较可看出管腔内的压力图像在不同膜压比下尾部波形存在差异。在膜片为0.07 mm时，两种管腔长度设计下膜片破碎后接触面运动速度小，反射稀疏波将超过接触面先到达底端面，导致平台结束，压力下降。在膜片为0.3 mm时，2 m∶9 m的设计反射稀疏波很快到达底端面，导致压力平台快速下降，4 m∶7 m时稀疏波与接触面到达端面时间相近，平台时间下降较缓。在使用0.8 mm的膜片时，接触面速度较大，先于反射稀疏波到达底端面，使得反射激波在接触面上发生二次反射，从而再次到达底端面时使压力平台上升，平台时间结束。

根据实验数据，对两种管长设计在不同膜压比下的平台时间进行统计，结果如表7所示。

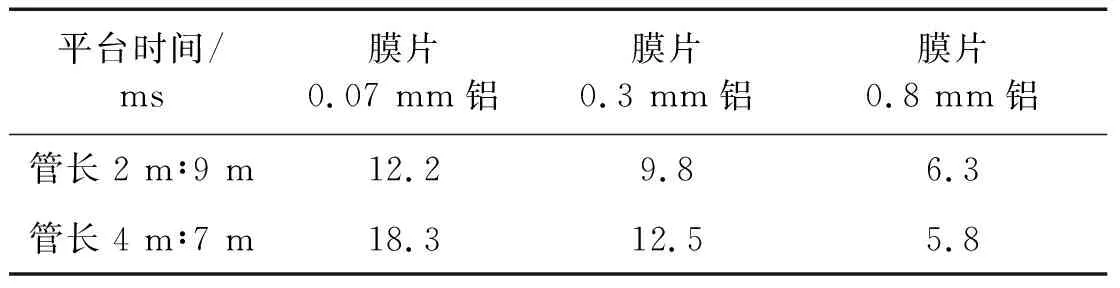
表7 不同初始状态下平台时间

可以看出平台时间的长短与管长设计有关，同时初始状态的膜压比不同也会导致平台时间的不同。

4 结 论

通过理论分析可知，入射激波的马赫数与初始状态的膜压比以及管腔内气体介质有关，同时可根据得到的马赫数来选择高低压腔的管长比，从而对阶跃平台时间进行优化，用以提升动态压力校准的实验范围。

通过对低压腔为大气压，三种膜压比情况下的两种不同设计方案进行仿真分析，可知在低马赫数时增加高压腔长度可以一定程度上提高阶跃平台时间。利用FLUENT仿真平台对三种情况进行模拟，结果表明在考虑黏性的情况下，激波速度在传递过程中不断衰减，在底端面形成的阶跃压力幅值要低于理论值。在近低压腔底端位置时，马赫数衰减系数近似线性关系，且随激波的马赫数增加而增大。实验验证了在激波管总长一定时，高低压腔长度设计对阶跃压力以及平台时间的影响，得到结论与仿真结果基本一致。