基于BP神经网络的围岩介质爆炸峰值压力预测

郭 璇， 马思远， 郭一帆， 张晓新

(1. 北京交通大学 城市地下工程教育部重点实验室，北京100044; 2. 北京交通大学 土木建筑工程学院， 北京 100044； 3. 华诚博远工程技术集团有限公司, 北京 100052)

鉴于爆炸事件(近年如2017年4月俄罗斯地铁爆炸等)对地下公共服务设施产生的巨大危害和严重后果，各国纷纷出台相应的防护设计规范：如印度国家标准局1973年制定地下爆炸结构安全性设计规范，美国陆军1983年制定《常规武器防护设计规范》[1]，美国国防部2008年公布结构抵抗偶然爆炸荷载设计手册等，地下公共设施的安全防范等级不断升级。

地下结构防护设计中爆炸荷载的确定是关键性难题[2-5]，考虑爆炸波在非线性地层中传播的复杂性如：岩土围岩特性、地下特殊空间中固-液-气对爆炸及测点参数产生的重要随机影响、复杂的时空演化效应等多因素交叉影响，围岩介质各点的爆炸应力即难确定又难复核。各经验公式存在适用范围离散，地层参数随机或误差修正及量化困难等问题。

由反射系数法简化求取围岩介质爆炸荷载峰值压力的既有研究如：Ляхов等[6]对岩石和土中不同形式冲击波传播规律及计算方法的研究及实验；周丰峻等[7]对饱和土应力波传播黏塑性模型的计算方法及应变硬化特性实验；Henrych等[8]区分岩石、黏性土和非黏性土介质，以各相体变为基础的变形机理推导绝热状态方程确定其压力值；叶亚齐等[9]通过对砂黏土不同深度的爆炸试验，给出炸药埋深对围岩介质压力的影响及不同埋深峰值压力经验式；王占江等[10]通过花岗岩化爆实验，给出按岩性分区围岩介质的应力衰减规律；Al-Qasimi等[11]对不同土质系列爆炸试验测定土中一点峰值振动速度和峰值孔压，提出峰值振速的预测公式；William等[12]开展地下爆炸试验，通过60组不同土质试验测得不同湿度凝灰岩、花岗岩和淤泥围岩介质的峰值压力、振速、加速度及相应经验公式；Leong等[13]对新加坡残积土的多组小比例爆炸试验，测定饱和/非饱和土3种爆炸比例距离的峰值压力，对比试验结果与TM-5-855-1计算公式的误差，修正衰减系数，采用爆炸比例距离立方根的数据处理方法替代平方根拟合结果，提出无量纲经验公式；市野宏嘉等[14]通过小比例爆炸试验，研究不同饱和度的中砂、山砂、黄土爆炸波的传播规律，给出含参数密度和饱和度的经验公式，并与Leong结果对比吻合较好；Gefken等[15]通过爆炸试验箱不同测点压力、振动速度和加速度等参数研究归纳四种饱和度砂性土的爆炸波传播规律等。

基于以上研究基础和成果可以看出，科学分析爆炸围岩介质波的传播规律，快速得到大量峰值压力的关键特征值，提取随机特征，迫切需要提升一种稳定可靠的快速实用算法，以便开展大量实测试验数据和理论归纳式之间的关系归纳和规律总结。

BP网络[16-17]是一种按误差逆传播算法训练的多层前馈网络，是应用较广泛的神经网络模型之一，方便提供简易算法和结果。BP网络或算法能学习和存贮大量输入-输出模式映射关系，无需事先揭示描述这种映射关系的数学方程，使用最速下降法作为学习规则，通过反向传播不断调整网络的权值和阈值，使网络误差平方和最小，迅速收敛，提高计算效率。作为一种基本的智能信息处理系统，BP神经网络法的核心功能及算法思想由基本拓扑结构包括输入层(input)、隐层(hide layer)和输出层(output layer)实现，本文尝试利用该方法处理爆炸实验数据，预测爆炸围岩地层中任一点围岩介质峰值压力特征区间，并考察该简易方法的实效性。

1 BP神经网络算法

人工神经网络模拟人脑结构和功能的信息处理系统，其近似信息处理的有效性取决于层与层间高度的互连结构，每层可由多神经元组成，各神经元通过权重分配连接至下一层，形成的基本模型通过数学计算工具实现结构传递和层间有机联系。

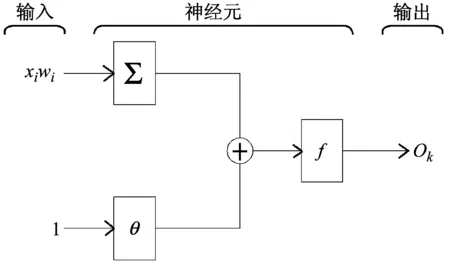
图1 神经网络模型示意

神经网络模型的基本流程和示意如图1所示，x1～xn由上一层神经元传来输入信号，wi表示神经元之间的连接权值，θ表示初值为1的阈值，f为传输函数，第j

个单元的输出值可由公式1给出：

(1)

利用输出层的各输出值误差，限定给出直接前导层的误差，并对权值和阈值更新，层层反向调整，直至误差减小到预设值。主要算法结构由输入层、隐层和输出层组成，流程主要分为两部分。

(1) 数据正向输入：权值和阈值初始化之后，网络随机选取一组输入向量(x1，x2,…,xn)和一组输出向量(y1，y2,…,yn),隐含层的输出值如公式1所示，则输出层第k个单元的输出值为：

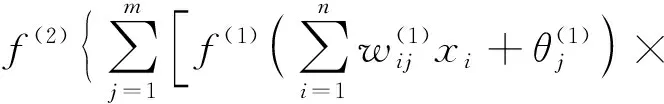
(2)

式中：标号(1)为输入层到隐含层的传输函数、权值和阈值，标号(2)为隐含层到输出层的传输函数、权值和阈值，m为隐含层单元数。

(2) 误差反向传递：用输出层误差对前向权值和阈值进行网络训练修正。本文选取Levenberg-Marquardt[18]算法作为训练函数，结合高斯-牛顿算法和梯度下降法的优点，具有较快的收敛速度。e(X)表示每个输入样本X在输出层的残差，X为权值和阈值组成的向量，XN表示第N次迭代，则基本算法可表示为：

XN+1=XN-(JTJ+λE)-1JTe(X)

(3)

式中：E为单位矩阵；λ为正数，在迭代中不断调整，使JTJ+λE保持正定矩阵；J为雅各比矩阵：

(4)

式中:K为X向量维度，l为输出层单元数。

完成初始修正后，随机选取下一组数据继续上述过程，直至输出误差达到预设值或趋于稳定，直至整个网络收敛。

2 BP神经网络构建

2.1 数据集

本文收集130个地下封闭爆炸实验数据(William&Robert、E.C.Leong、Hiroyoshi Ichino、Paul R.Gefken等)，根据实验土质，将围岩数据初分为：黏土、砂性土和岩石三组，各组自动随机5个数据作为测试样本，取值在表1中列出。输入参数包括介质参数：纵波波速c、密度ρ和饱和度S，使用爆炸比例距离D来描述位置参数和炸药参数，(此处定义D=R/W1/3，R为距离爆炸中心的距离，W为炸药的TNT当量)。考虑爆炸比例距离和峰值压力的数值量级差别较大，将其对数化处理。

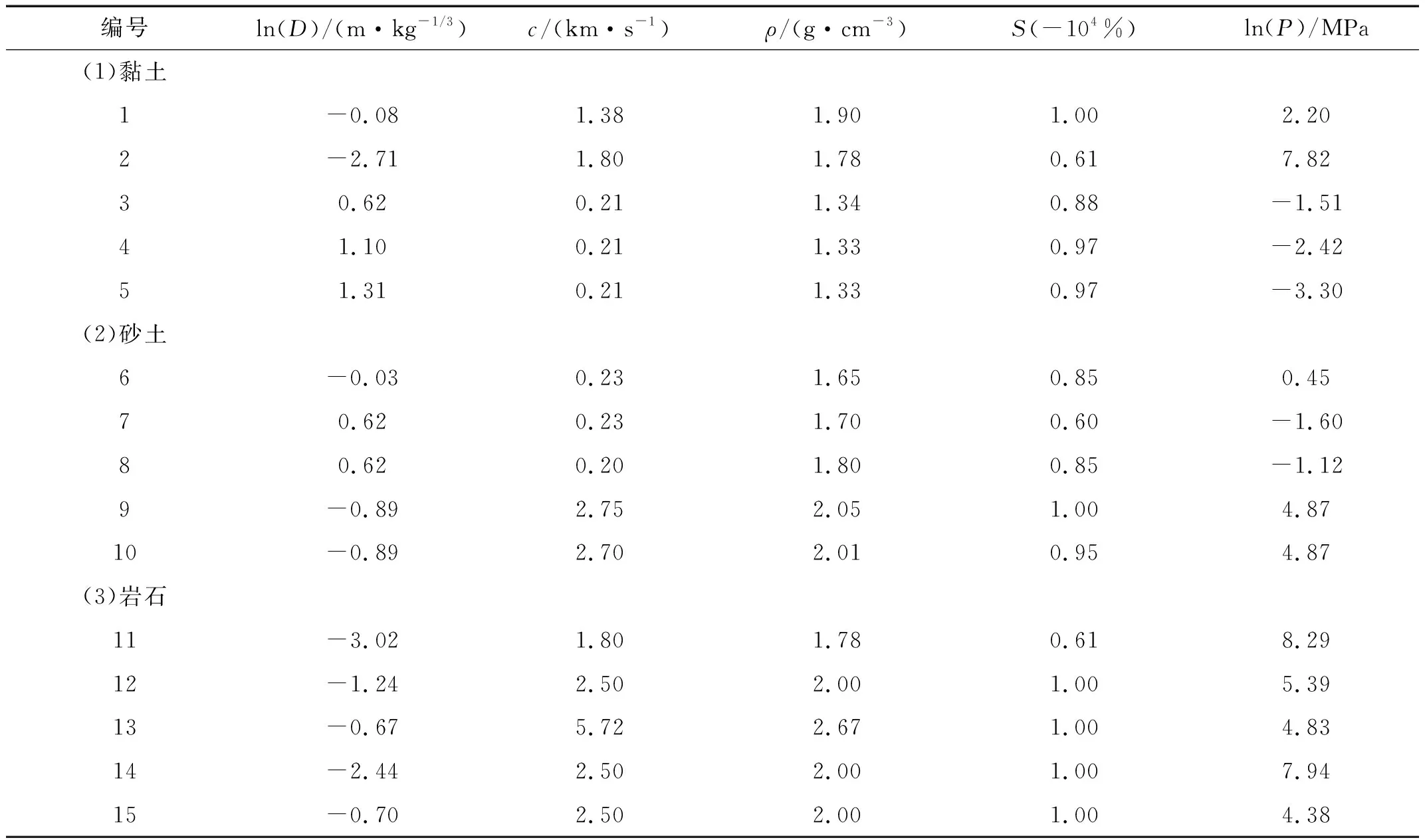
表1 测试样本

输入和输出参数及其范围如表2所示。

表2 输入输出参数取值范围

2.2 网络构建

输入和输出层分别有4和1个神经元，网络性能受隐含层神经元数量影响较大，通过经验公式(5)限定范围，逐步试验得出最佳节点数。

(5)

式中：α为1～10之间的常数。

为试验得到最佳网络性能，共建立了30个BP神经网络，隐含层神经元个数分别为3～12。网络选用双曲正切S型函数tansig作为输入层到隐含层的传输函数，隐含层到输出层选用线性函数purelin。通过软件Matlab®函数newff命令建立网络。将测试样本输入网络，得到结果与实测值均值的绝对误差MAE为：

(6)

得到不同网络的MAE在图2中列出，可以看出，黏土和岩石隐含层节点数为6时，网络均值的绝对误差最小；砂性土的隐含层节点数为7时，预测性能最好。选用各组最佳网络预测峰值压力，通过net.w和net.b命令可查看训练完成的权值和阈值，得到预测表达式：

ln(P)=[tan sig(W1X+θ1)]W2+θ2

(7)

(8)

式中：P为峰值压力；X为输入矩阵[ln(D)，c，ρ，S]T；Wi和θi(i=1,2)为权值和阈值矩阵，取值在表3中列出。

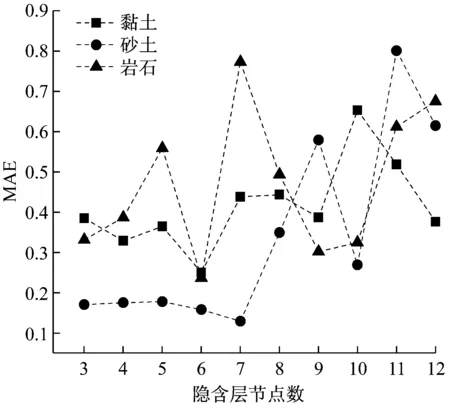
图2 不同网络的MAE

3 结果及分析

3.1 现有预测方法

(1) 经验公式：现有峰值压力公式的能力表现可通过对比美军常规武器防护规范TM5-855-1的建议方法进行。Robert等[12]根据不同介质的实验数据给出拟合公式，Leong等[13]通过爆炸试验提出了无量纲化预测模型，市野宏嘉等[14]通过爆炸试验和参数分析得出含饱和度S和密度ρ的预测公式，各具体公式的形式对比在表4中列出。

(2) 选择多元回归分析(Multiple Value Regression Analysis，MVRA)作为建议方法效果的检验方法。MVRA方法建立多自变量和一因变量之间的数学关系，通过判断几个特定变量间是否存在相关关系，找出函数间合适的数学表达式。将网络输入参数作为自变量，输出参数作为因变量，通过软件Origin Pro®得到本算例的多元线性回归表达式：

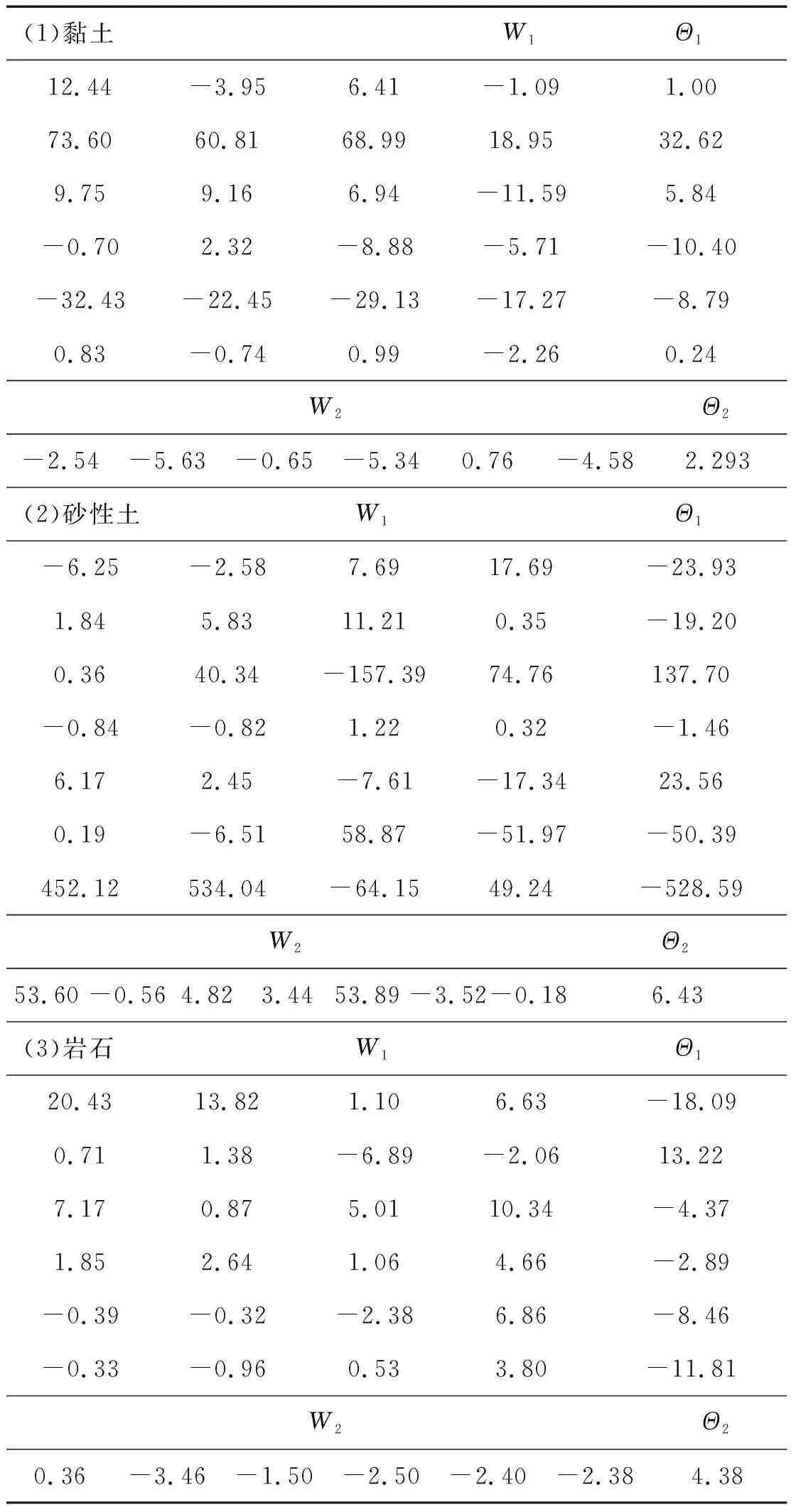
表3 网络参数表

表4 经验公式

ln(P)={-2.804 91×D[kg/m1/3]+0.144 49×

c[km/s]+0.693 87×ρ[g/cm3]+

2.354 39×S[104%]-2.659 25}

(9)

3.2 结果检验

为验证预测方法的可靠性，使用15个未参与训练过程的数据对BP神经网络和多元回归分析(Multiple Value Regression Analysis，MVRA)预测方法的预测效果进行相互测试和对比；考察各方法计算结果的参数效应。

图3列出基于各预测方法的预测值和实测值对比分布情况，供效果判断。

对比各图分布效果可以看出，BP神经网络具有较好的拟合效果，对不同参数的预测偏离度较小；各经验公式在某些区间或节点上的准确度较好，但整体误差和离散程度较大，在变换不同参数时的准确度变化大，预测效果出现不稳定。

此外在黏土、砂土、岩石不同介质各方法预测效果的对比结果可知，MVRA的拟合性整体优于经验公式，图4中6种预测模型预测值的MAE值对比可以看到，BP神经网络预测方法平均误差最小，在0.5以下，预测效果最好，对砂性土的预测最为准确；各经验公式由于在不同参数区间的准确度不一，个别区间偏离严重，整体平均误差比BP神经网络法及MVRA均大，三种方法对比而言，在此例岩石类数据的预测结果中误差出现了偏大现象。MVRA整体预测误差能力介于中游，对于黏土的预测误差最小。

3.3 地下结构防护设计的实例分析

为进一步考察方法的实用性，开展方法的实例应用分析。将以上各方法在具体岩层条件下地下结构爆冲荷载的防护设计中进行对比，进一步考察模型的预测效果。

假定爆炸围岩介质中地下结构防护设计的爆冲峰值荷载Pr的主要影响因素和条件为：

(1) 围岩介质峰值压力Pso：主要影响因素为位置参数和介质参数；

(2) 炸弹等震源耦合系数f：与爆炸埋深和炸药量有关，封闭爆炸耦合系数取1；

(3) 考虑爆炸波在土-结构交界面多次反射、相互叠加，峰值增加效应。

Pr通过下式简化计算：

Pr=f×N×Pso

(10)

式中：N为放大倍数或反射系数。

根据Hailong等对埋入式钢筋混凝土拱结构在爆炸荷载作用下的响应问题进行的试验研究[19]，在不同TNT炸药量下测得结构和围岩介质的压力时程变化，选取P2和P3位置的测点数据为研究对象，P2测得围岩介质压力，P3测得拱顶反射荷载值，反射系数在6 kg和17.4 kg药量下分别取1.55和2.1，耦合系数为1。测点和炸药位置示意，如图5所示，试验场地土质为风化砂质黏土，密度ρ为1 810 kg/m3，纵波波速为1 025 m/s，含水率ω为25.2%，取颗粒密度ρs=2 600 kg/m3，水密度ρw=1 000 kg/m3，则，饱和度：

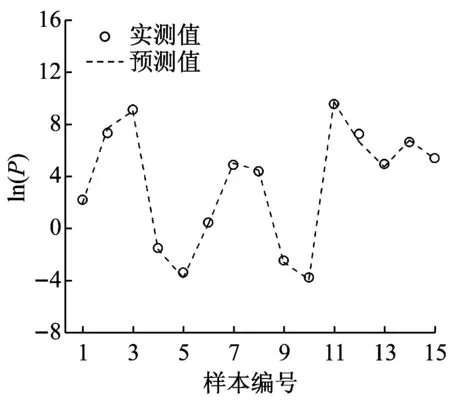
(a) BP神经网络

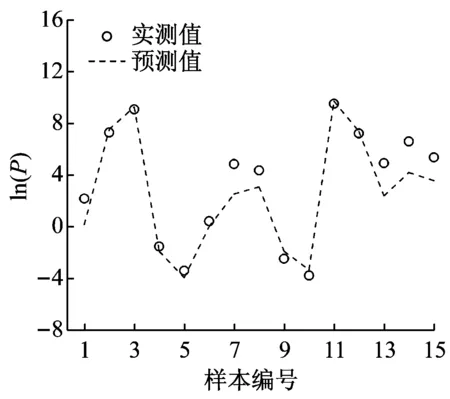
(b) TM5-855-1

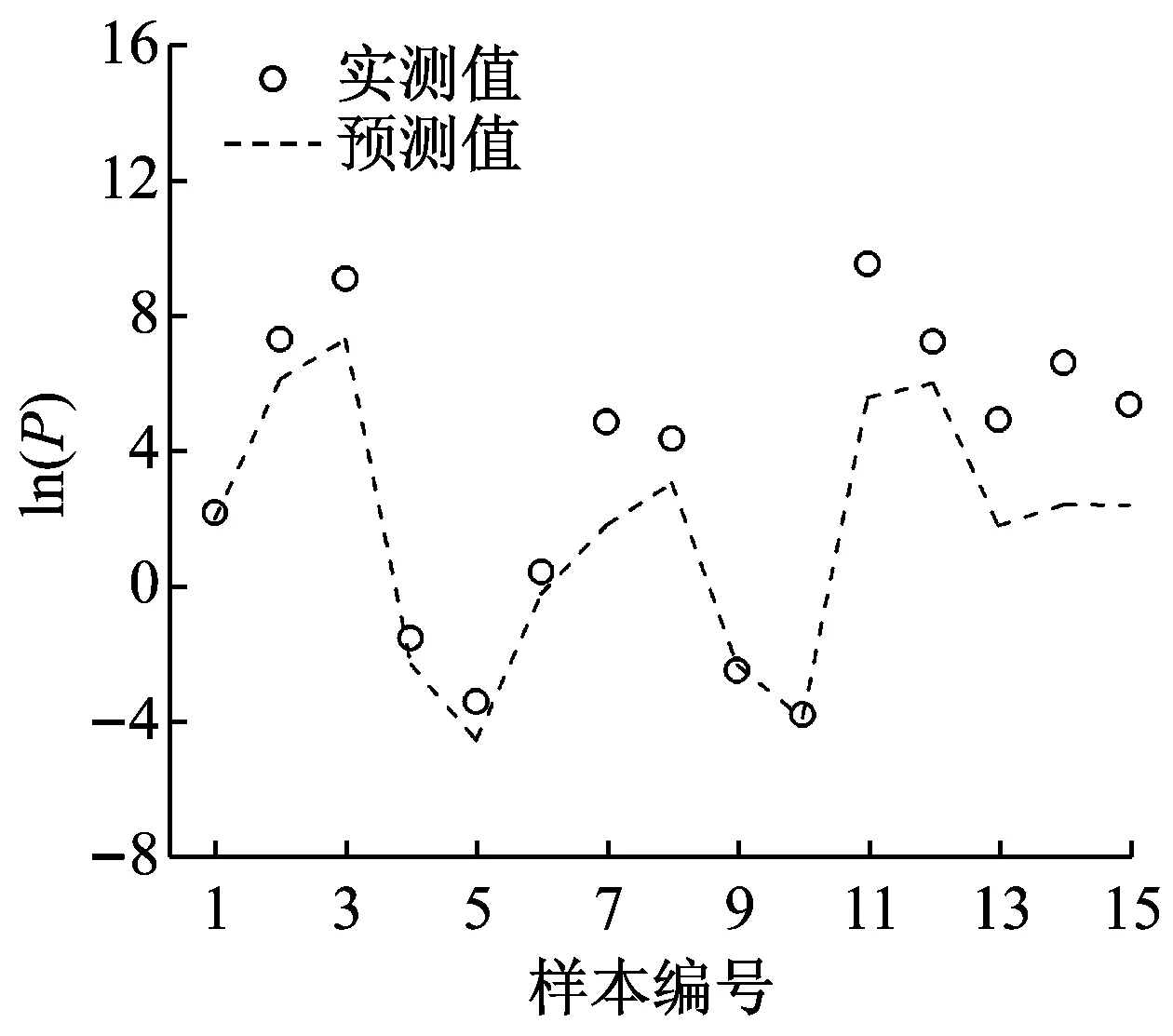
(c) Leong

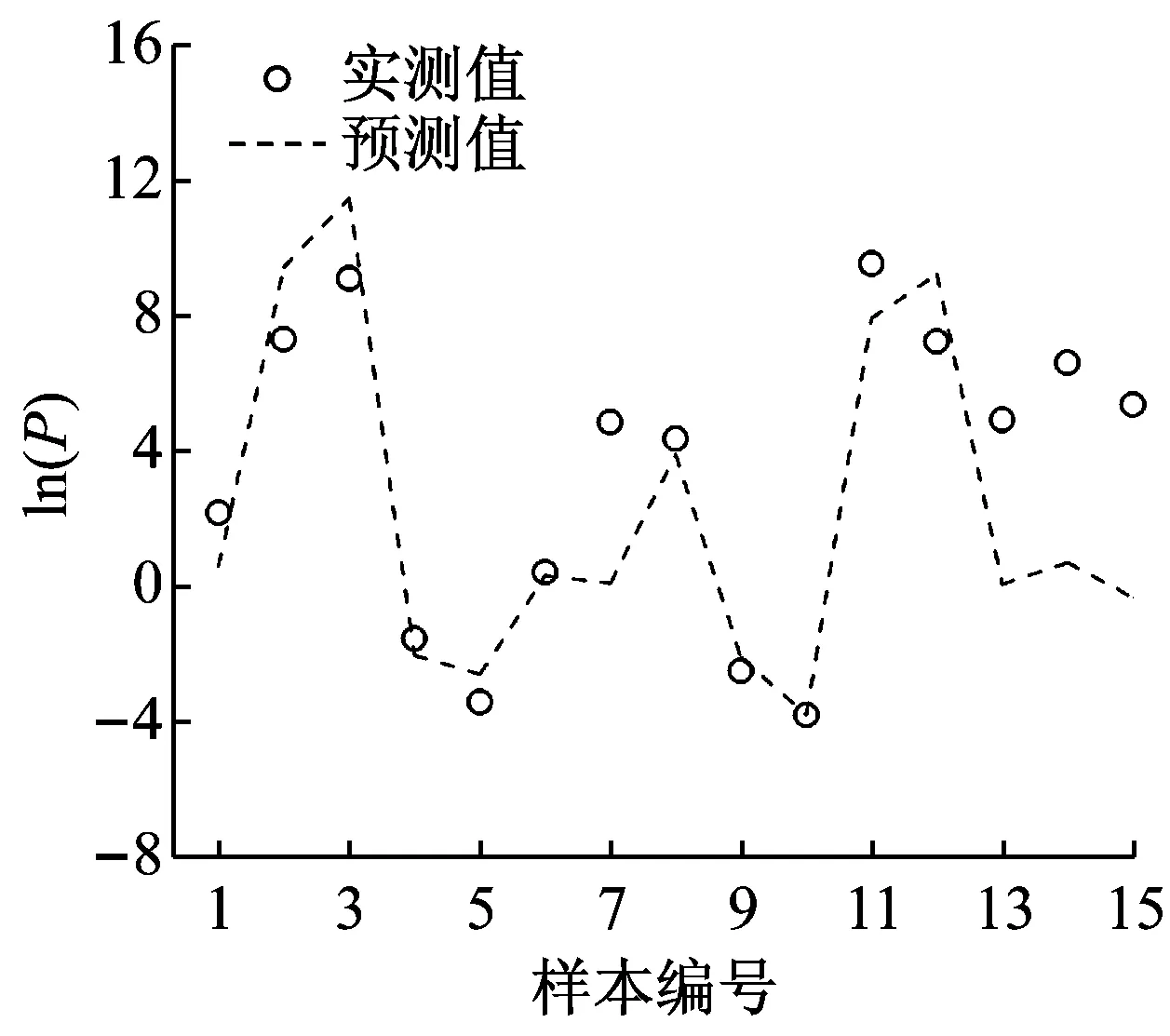
(d) Robert

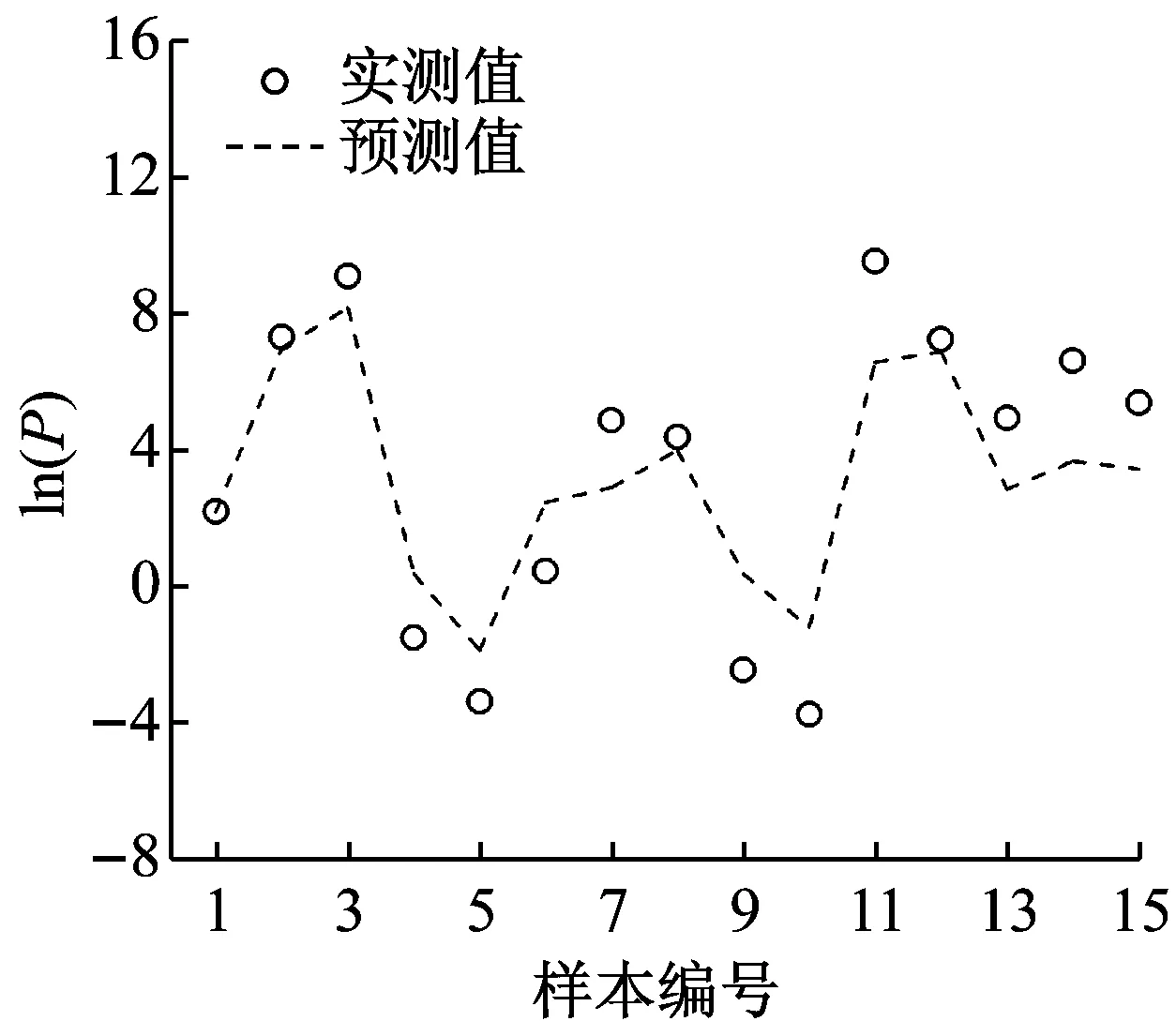
(e) Hiroyoshi

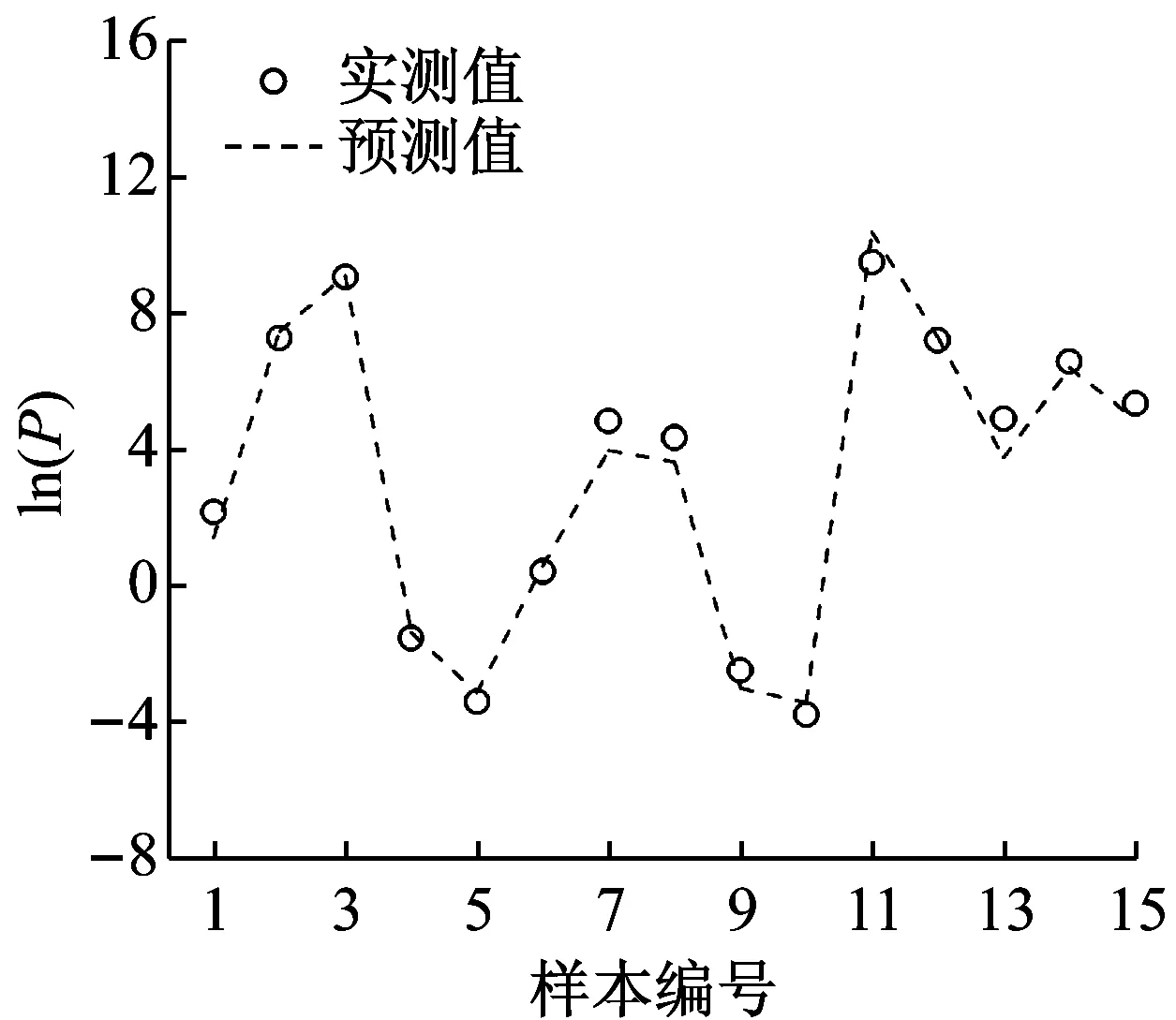
(f) MVRA

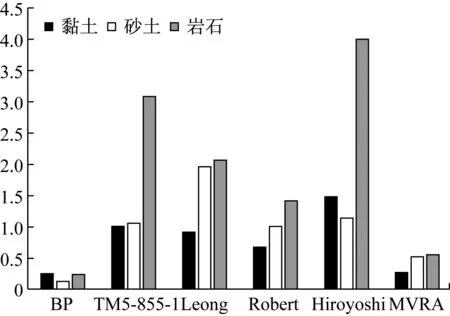
图4 预测结果的MAE

(11)

将以上参数输入到BP神经网络模型，训练完成后和MVRA模型分别得出P2，P3的围岩介质峰值压力，进而得到P3点的爆炸荷载，计算值和相对误差在表5

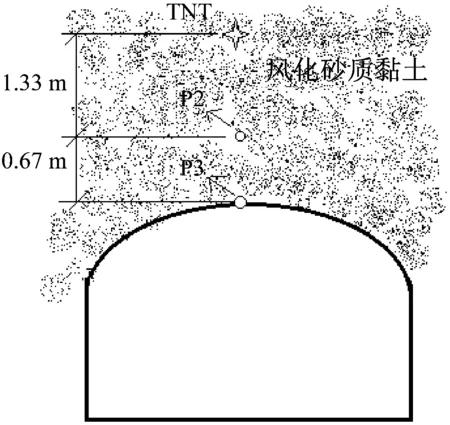
图5 测点和炸药位置

中列出，对比得到BP神经网络的预测结果与实测值较接近。

3.4 敏感度分析

为考察各参数对峰值压力结果的影响程度，进而开展多自变量参数变化的敏感度层次分析。使用余弦振幅法评估输入特征参数：纵波波速、密度和饱和度等参数对结果的影响程度[20]。每参数的所有数据用空间V表示。

V={v1,v2,v3,…,vn}

(12)

vi={vi1,vi2,vi3,…,vim}

(13)

式中:v为空间V的长度;为m向量;n为参数个数;m为数据个数。

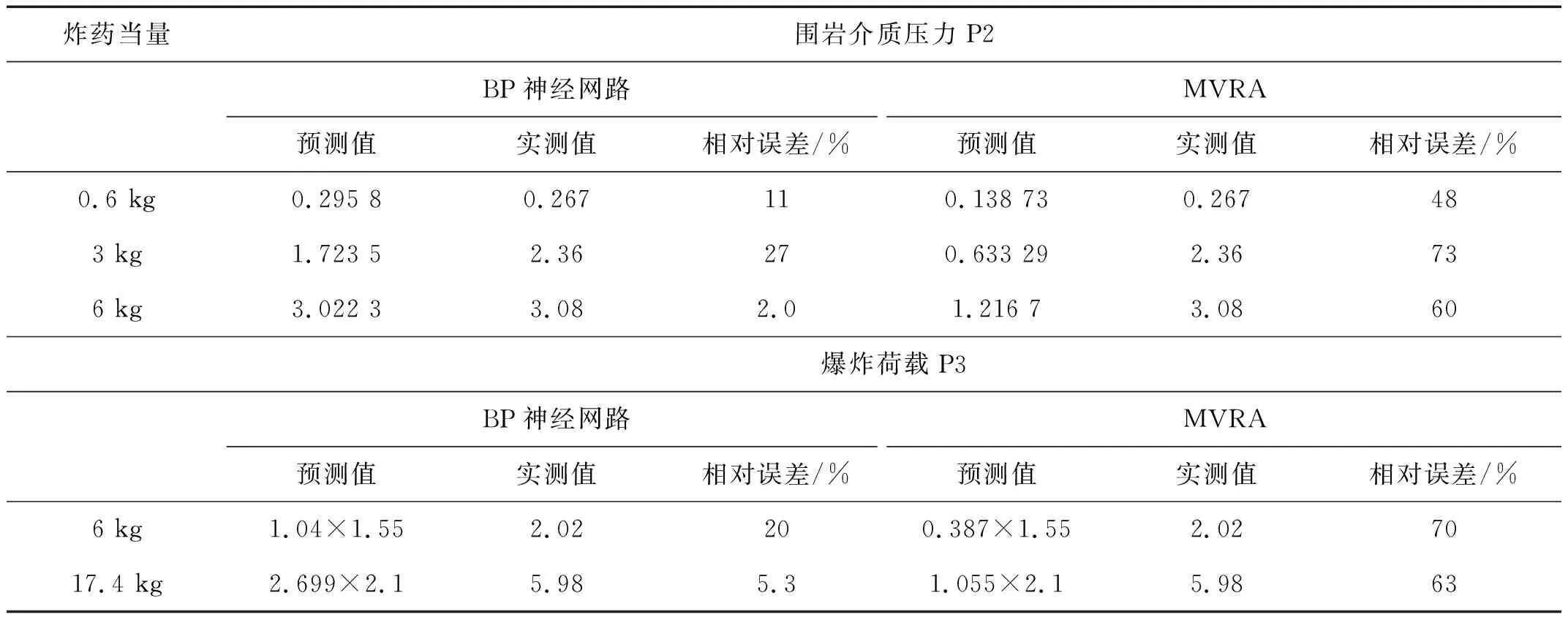
表5 P2和P3误差预测

每个数据集可被认为是m维空间中的点，任意两个数据集vi和vj间的影响程度可由式(14)得出。

(14)

黏土、砂土、岩石介质的特征参数敏感度对比分析如图6。对比可以看出，三种地层介质中纵波波速对结果的影响都最为明显和显著；黏土和岩石地层中饱和度对结果影响最小；砂性土中敏感度最低的特征参数是密度。

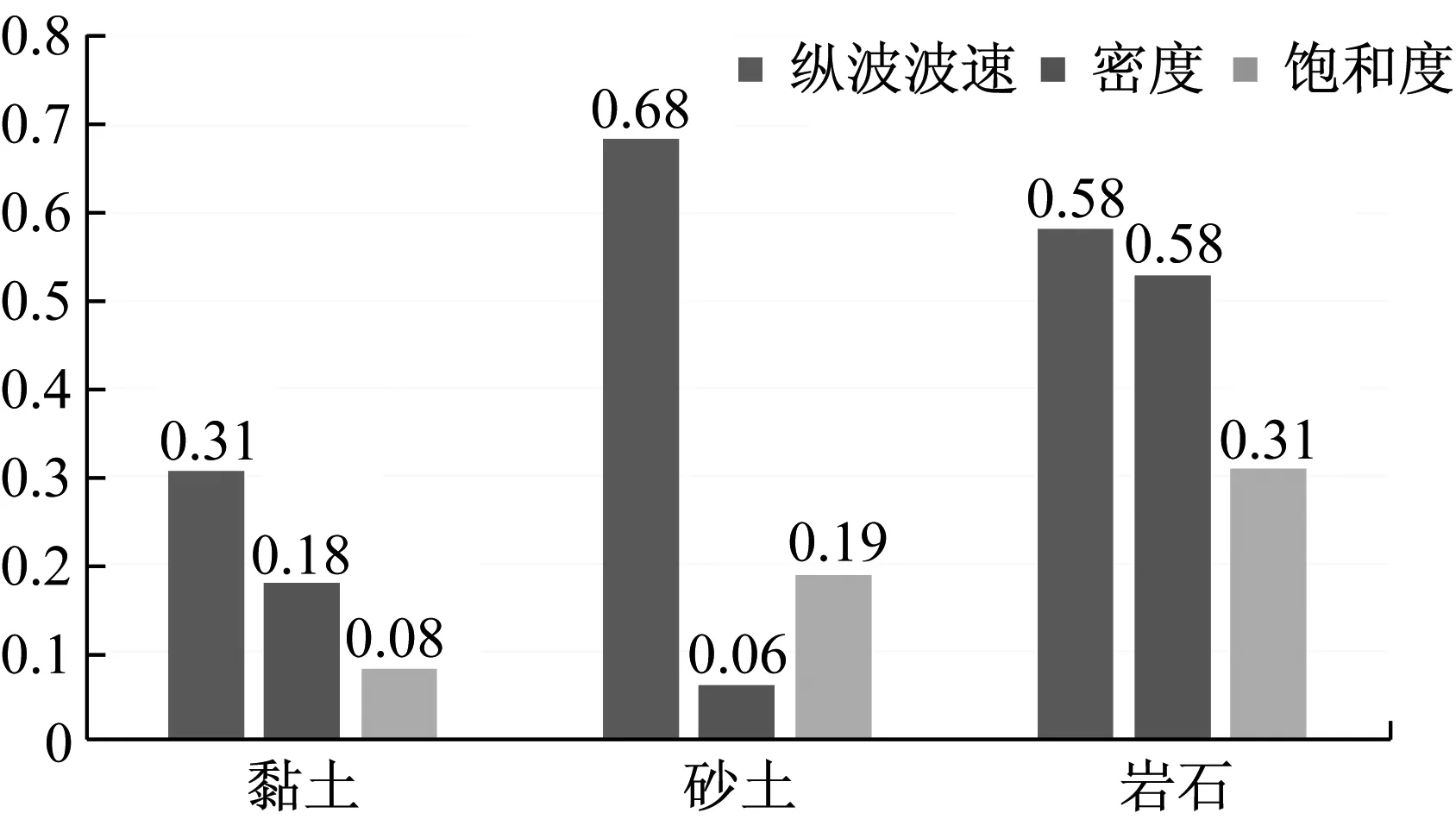
图6 特征参数的敏感度分析

4 结 论

以上基于BP(Back Propagation)神经网络法，通过分析130个地下封闭爆炸实测数据，区分黏土、砂性土和岩石三组地层介质，给出一种爆炸围岩介质峰值压力的简易预测方法和评价；通过分析特征参数：爆炸比例距离、土体纵波波速、密度和饱和度等产生的影响，将输出BP神经网络模型的爆炸围岩介质峰值压力特征和实例结果对比，认为：

(1) BP神经网络模型能够快速处理复杂非线性映射，区分黏土、砂性土和岩石三组介质数据，根据爆炸比例距离、纵波波速、密度和饱和度等特征参数，可分别建立相应网络，当隐含层单元数分别为6、7、6时，输出的峰值压力值获得最佳网络性能。

(2) 利用测试样本对BP模型、美军规范及类似经验公式的效果对比中，BP神经网络得到预测结果的平均误差最小，其三组测试数据的误差都小于0.5，相比各经验公式优势明显，预测性能也好于MVRA。

(3) 在工程实例的应用中，考虑介质反射系数进行风化砂质黏土地层爆炸围岩介质峰值压力的预测，输入工程实例参数的BP神经网络和MVRA模型的结果对比，BP神经网络的爆炸荷载预测值相对误差在20%以内，优于MVRA。进行了三种介质地层各特征参数的敏感度分析，各围岩介质的纵波波速对其峰值压力的影响均最为明显，黏土和岩石地层饱和度的敏感度较小，对砂性土影响最小的介质参数是密度。

以上基于BP(Back Propagation)神经网络法,提出一种土中任一点围岩介质峰值压力的简易评价和预测方法，并通过与经验法对比，部分验证了方法的实效性。建议方法可为预测地下结构防护设计中爆炸荷载的响应峰值提供一种算例参考。