雷管延期误差对地震波叠加降振的概率分析

韩 亮， 李红江， 刘殿书， 凌天龙， 李 晨， 梁书锋

(1.华北科技学院 安全工程学院，北京 101601；2.中国矿业大学(北京)地球科学与测绘工程学院，北京 100083；3.中国矿业大学(北京)力学与建筑工程学院，北京 100083)

从地震波叠加的角度来看，利用微差爆破实现干扰降振主要涉及两个问题：一是最优微差时间如何确定；二是能否保证起爆时间的准确性。对于问题一，文献[1-4]分别从振幅、主频及能量方面研究了双段叠加波形的时频特征，并提出了最优微差时间的确定依据，但并未考虑传播距离的影响，由于爆破地震波为非平稳信号，随距离的增加，叠加波形的时频特征将更为复杂。对于问题二，文献[5-7]利用高精度电子雷管进行了爆破振动控制研究，均取得了较为理想的效果，但研究多限定在试验及特定工程中，由于电子雷管价格昂贵，目前还无法大规模应用于现场，因此，其研究成果的借鉴意义有限。

鉴于此，本文在现场试验基础上，利用等间隔延时双段叠加方法分析微差时间对降振率的影响随传播距离的变化情况，并确定了不同测点处满足降振的最优微差时间，同时，在考虑雷管延期误差的基础上，引入概率模型定量分析延期误差对地震波叠加降振的影响，计算结果可为爆破设计提供一定的参考依据。

1 双段叠加最优微差时间与距离的关系

1.1 单孔波形的选取

试验场地选择在北京昌平区凤山矿+42平台，现场以坚硬石灰岩为主，岩体完整性较好。在爆区后方共进行七次试验，测得54组单孔垂向波形。振速与主频衰减规律,见图1。

为保证所选单孔波形能够代表上述试验场地条件下，同一信号随距离的变化情况，所选波形需满足如下条件：

(1) 振速和主频应与各自回归曲线的残差为0或接近0；

(2) 爆心距由小到大，应能体现出不同距离下单孔波形的时频特征。

共选出5组满足条件的单孔波形，见图2，对应的时频信息见表1。

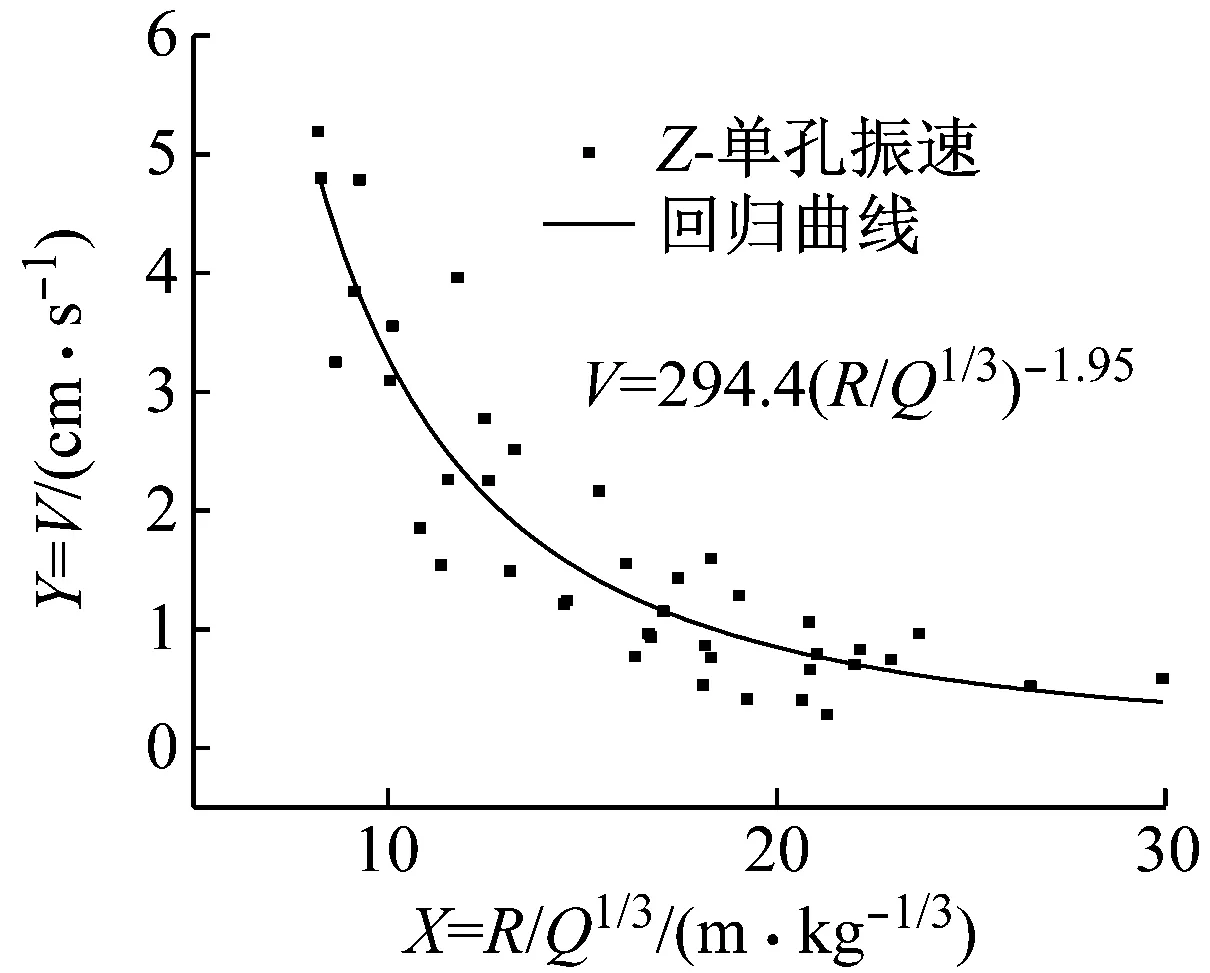
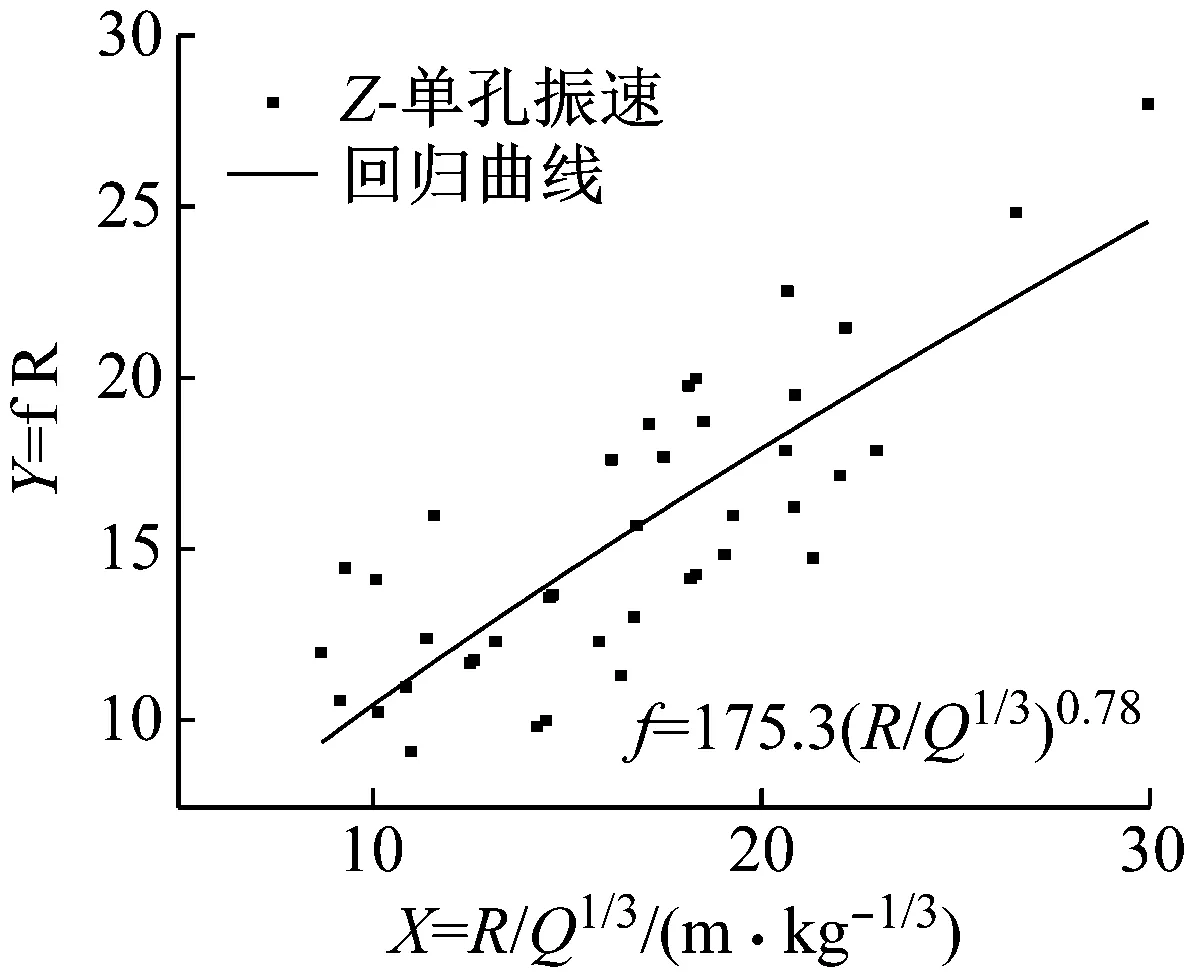
图1 单孔垂向振速衰减规律及主频统计规律

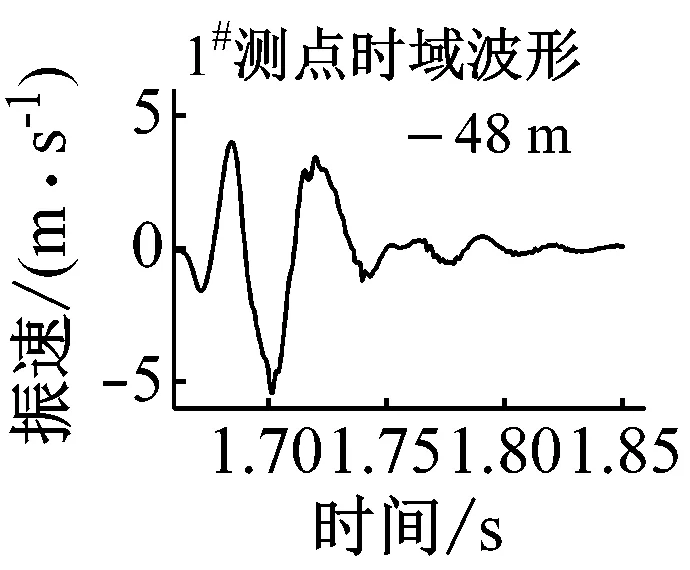
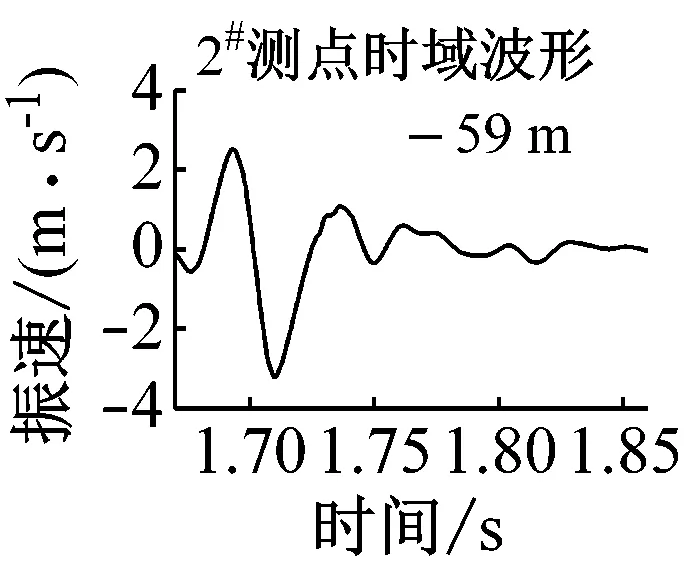
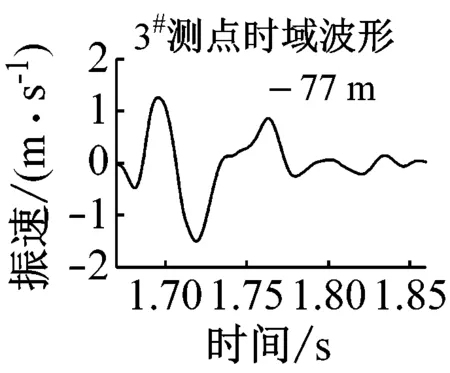
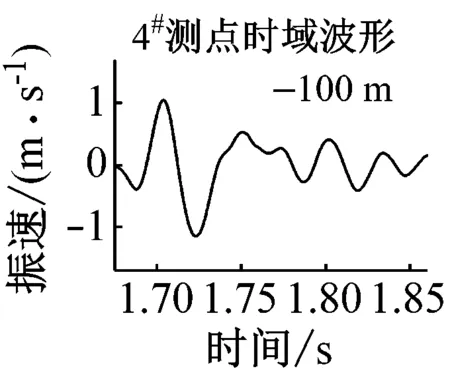
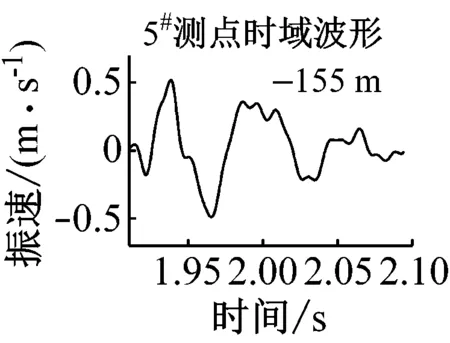
图2 各单孔震波时域波形

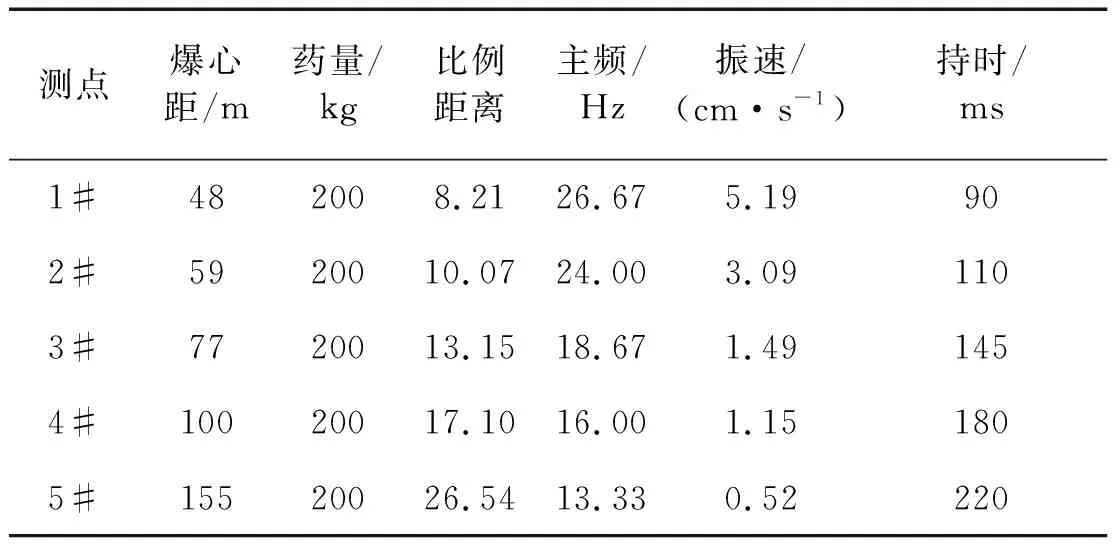
测点爆心距/m药量/kg比例距离主频/Hz振速/(cm·s-1)持时/ms1#482008.21 26.67 5.19 902#5920010.07 24.00 3.09 1103#7720013.15 18.67 1.49 1454#10020017.10 16.00 1.15 1805#15520026.54 13.33 0.52 220

1.2 微差时间对振速的影响随距离的变化

用Matlab编制程序，在0～190 ms内分别对1～5#测点进行间隔时间为1 ms的双段叠加。分析微差时间对降振率[8]的影响随距离的变化规律。不同距离处测点降振率随微差时间的变化情况,如图3所示。

(1) 叠加信号的降振率总大于齐发爆破，且与测点爆心距无关；

(2) 随传播距离的增加，最大降振率所对应的微差时间也逐渐增加，但由于爆破信号并非平稳信号，当微差时间为半周期整数倍时，并不一定对应最大降振率，因此，对于干扰降振而言，更应关注的是某一微差时间段而非某一时刻；

(3) 随传播距离的增加，局部最大降振率出现了多峰值的现象，同时，降振率较低的微差时间段逐渐增多，这是因为传播距离增加后，波形持续时间增大，波峰与波谷增多，地质条件对波形的影响逐渐增大；

(4) 由于地质条件的不确定性，随着传播距离的增加，爆破地震波将出现明显的多主频性，干扰降振的难度逐渐增大。总体来看，降振率随传播距离的增加而降低。

1.3 最优微差时间与距离的关系

不同距离处测点振速幅值随微差时间的变化情况,如图4所示。

图4中，振速幅值小于单孔波形的部分用深黑色部分表示，在不考虑主频的情况下，将其对应的微差时间段称为最优微差时间，48 m处为15～25 ms，59 m处为17～28 ms，77 m处为19～30 ms，100 m处为22～34 ms，155 m处为37 ms。如图5所示,最优微差时间接近波形的半周期，随传播距离的增加，最优微差时间逐渐增大。图5中5#测点相对较远，单孔波形较复杂，叠加后最优微差时间并非为一时间段，而是一个时刻。

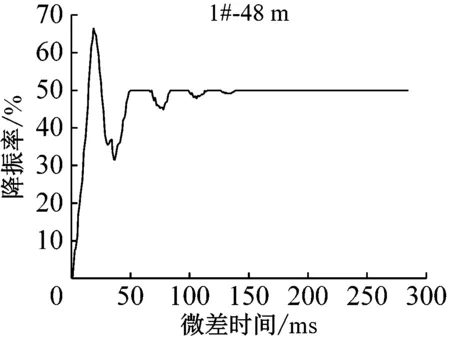
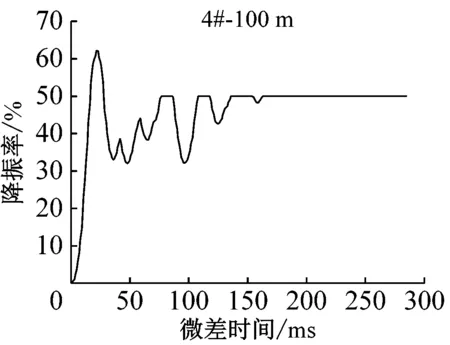
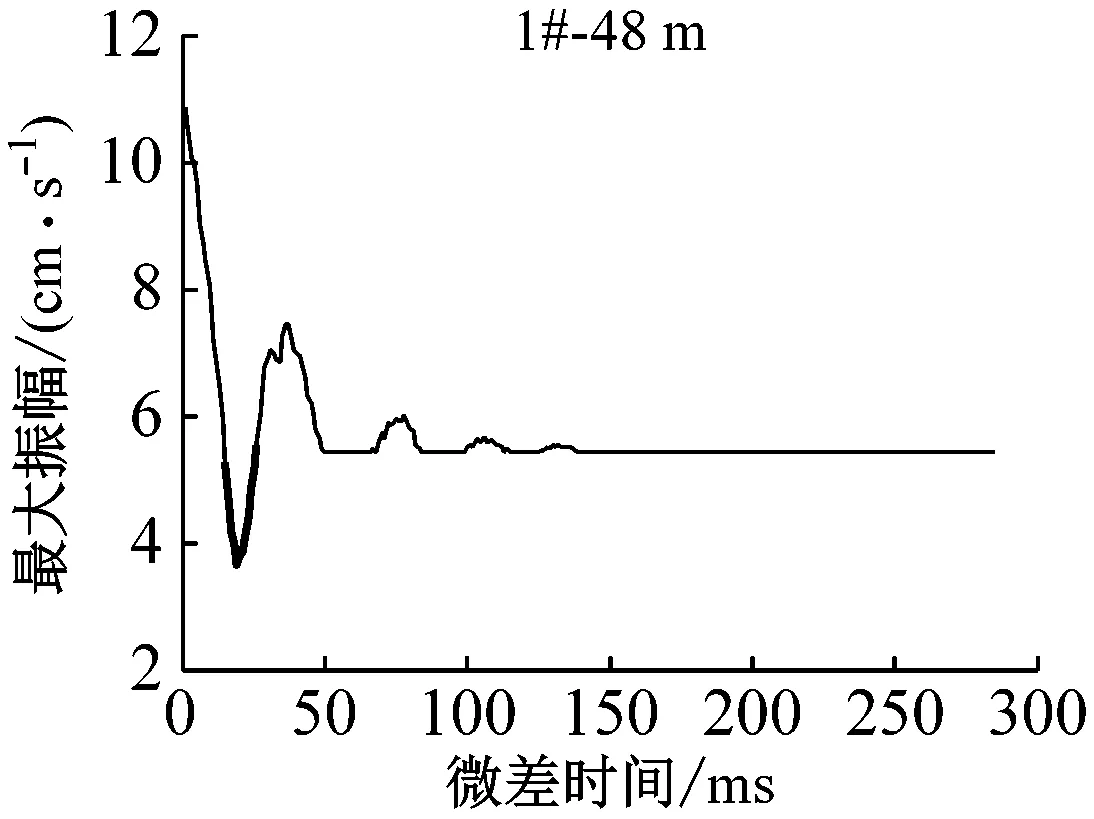
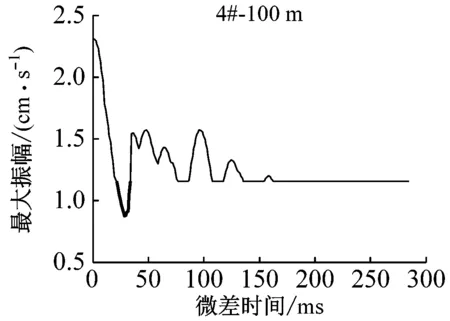
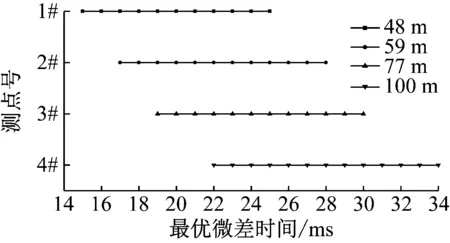
图5 各测点最优微差时间分布

2 雷管延期误差的概率计算

2.1 计算方法概述

雷管延期误差ti可看做随机变量，当某段雷管同一批次的数量足够大时，服从正态分布，记为：

ti～N(0,σ2)

(1)

式中:ti是指同一批次内，与实际起爆时间总体均值的偏差，而非名义起爆时间。

计算数据引自文献[9]某批次抽样实测的MS1～MS15非电毫秒雷管延期时间，见表2。

若对本批次进行多次抽样，得到的延时均值及样本标准差也将有所变化。由于标准差与雷管段别正相关，因此，可建立回归方程计算指定置信水平下不同段别雷管的标准差，并将置信水平上限作为本批次雷管延期偏差的最不利情况，进而分析其发生的概率。

2.2 标准差回归

建立回归方程，根据最小二乘法对a和b进行参数估计[10]，

y=ax+b±ε

(2)

式中：y为回归标准差；x为各段雷管延时均值；a,b为回归参数；ε为余差。

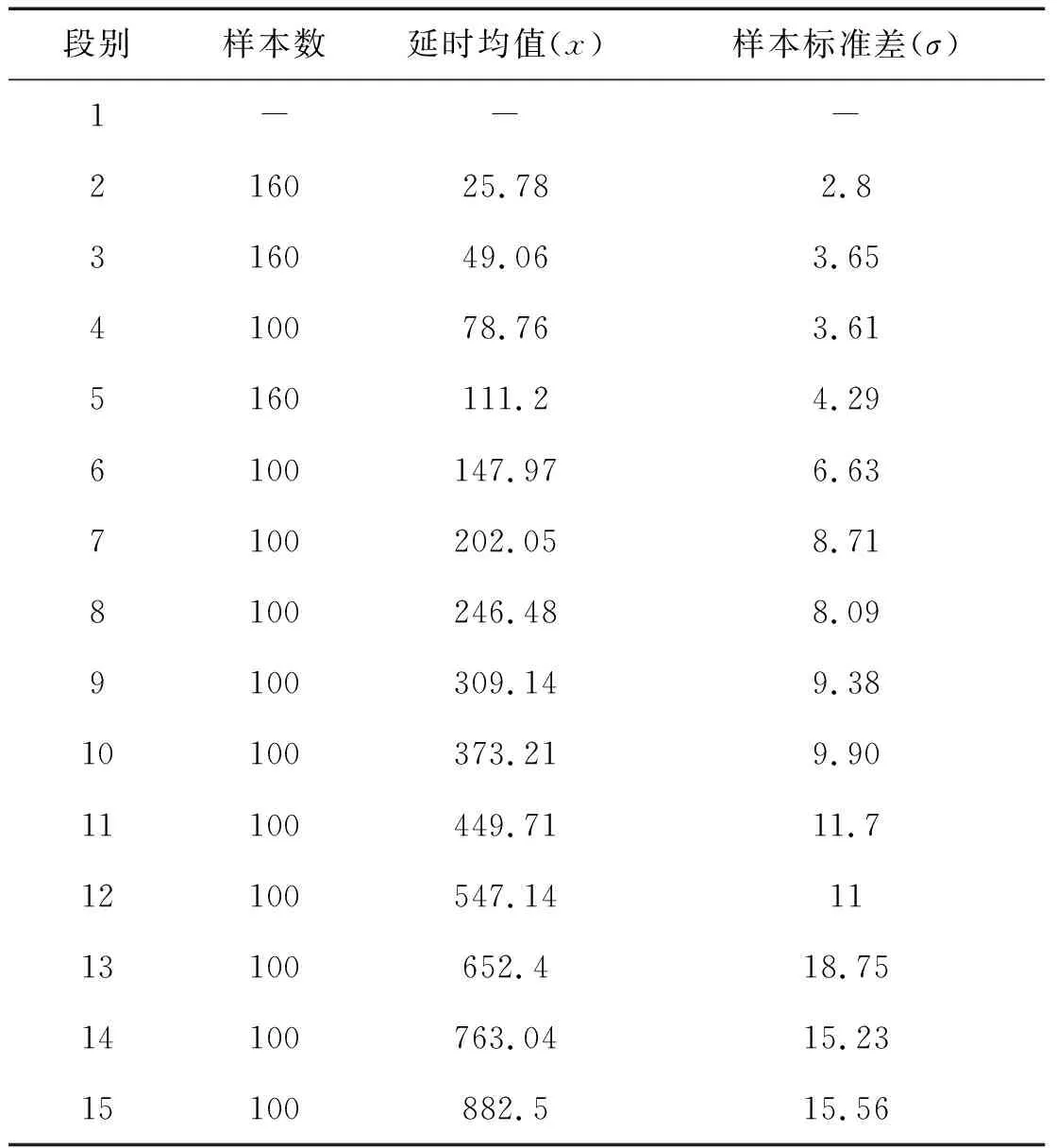
表2 非电毫秒雷管统计

计算得到的95%置信水平下各段雷管的标准差分布区间,如图6所示。

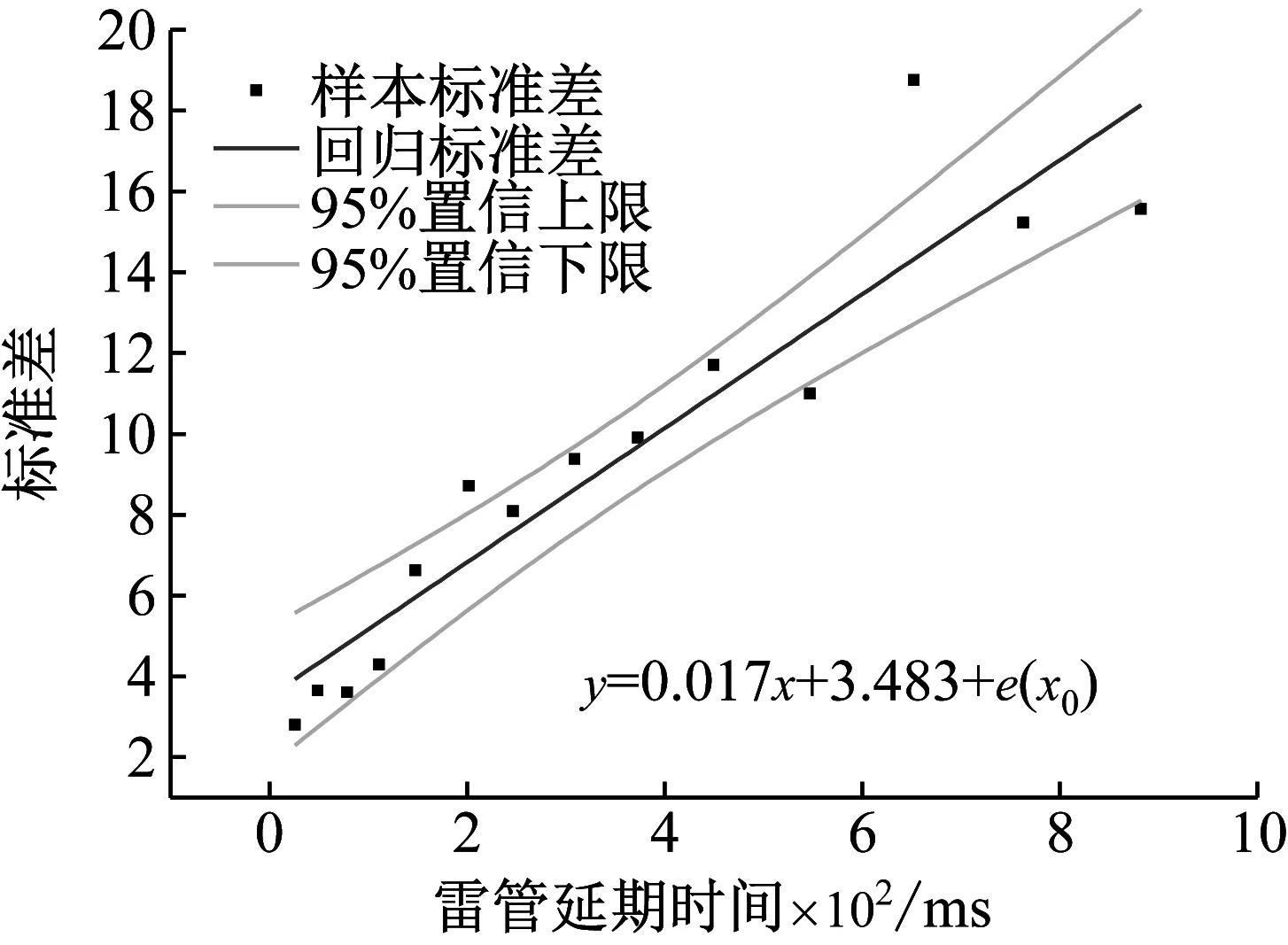
图6 雷管样本标准差回归分析

计算得到的回归曲线方程为：

y=0.017x+3.483±ε

(3)

式中:ε的计算见式(4)，表示当x取值为x0时，余差ε的计算值。

ε(x0)=

(4)

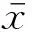
由于雷管精度随段别的升高而降低，因此，本文主要研究高段位雷管(MS10～MS15)的延期误差概率。根据各段别的标准差回归方程式(3)，取95%置信水平上限作为不同段别雷管的标准差，见表3。

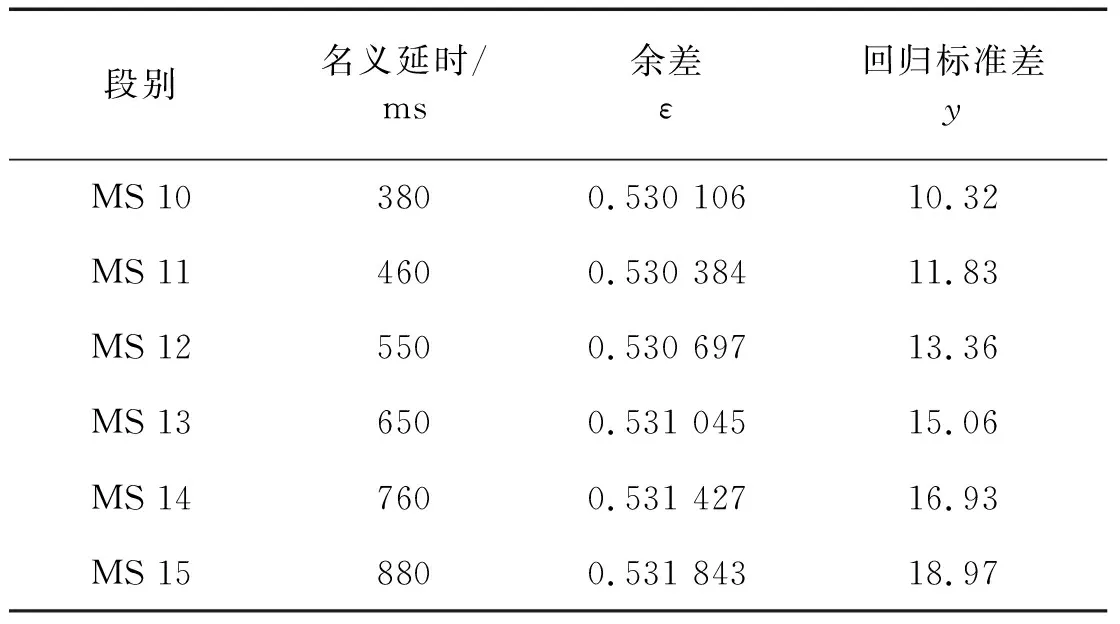
表3 标准差计算结果

2.3 延期误差概率计算

以MS10雷管为例，由样本数已达到100，为分析简便，将回归得到的样本标准差y作为雷管延期误差总体分布的参数是可行的，式(1)可表示为，

ti～N(0,10.322)

(5)

当取95%置信水平时，延期误差区间为(-1.96σ，1.96σ)，即，(-20.23 ms,20.23 ms)。

由概率密度分布函数：

(6)

通过对任意延期误差区间积分，即可求得任意延期误差下的概率：

(7)

由于概率密度曲线的对称性，正延时与负延时的概率相同，因此仅计算正延时一种情况，其余段别雷管延期误差计算方法同MS10，计算结果见表4。

3 延期误差对地震波叠加降振的概率分析

以1.1节中实测单孔波形双段叠加为例，假设两炮孔所装雷管段位相同(依次为MS10～MS15)，建立概率计算模型，通过Matlab编程计算因雷管延期误差而引起的干扰降振的概率，干扰降振的评判方法以两发雷管的实际起爆间隔落在图5所示的最优微差时间段为准。

3.1 概率计算模型的建立

在双段叠加的情况下，两发雷管以一定微差间隔Δt1～Δtn起爆的概率可以表示为:

(8)

式中：F(Δt1～Δtn)为两发雷管以Δt1～Δtn微差间隔起爆的概率；tj为雷管延期误差；±tm为雷管延期误差区间的上下限，数值为±1.96σ；F(tj)及F(Δti-tj)分别为雷管延期误差为tj及Δti-tj时的概率。

3.2 计算结果分析

利用式(8)对表4中各段延期误差对应的概率值编程计算，其中双段叠加降振的微差间隔为图5中不同距离测点最优微差时间的分布区间，可以得到不同距离测点处分别用MS10～MS15雷管双段叠加干扰降振的概率，如表5所示。

将表5数据对应图7。从图7中不难看出，各段别雷管由于延期误差而引起的降振概率在爆心距不同的测点也不尽相同。从降振概率数值来看，近距离测点，低段位雷管的降振概率较大，远距离测点，高段位雷管的降振概率较大；从降振概率的稳定性来看，低段位雷管的降振概率受测点距离影响较大，高段位雷管所受影响较小。上述计算从数理统计和概率的角度定量分析了不同段别雷管在不同测点处引起的双段叠加降振的可能性，在实际爆破设计中，可根据不同爆心距处所能承受的最大振速，对爆源处的雷管段别进行优化选取，为爆破设计提供有益的参考依据。

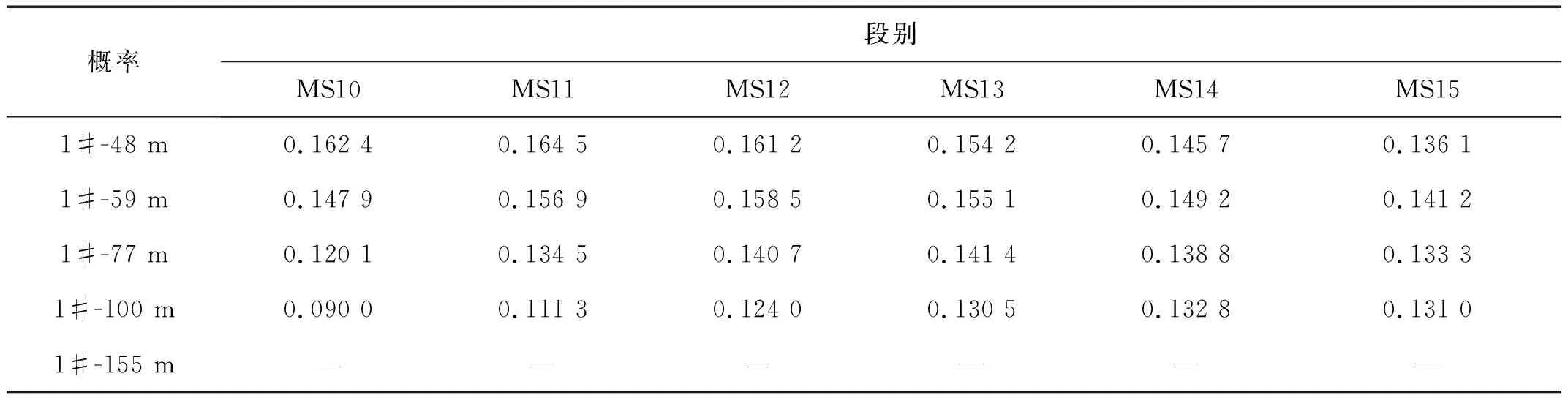
表5 不同测点处MS10～MS15雷管干扰降振概率

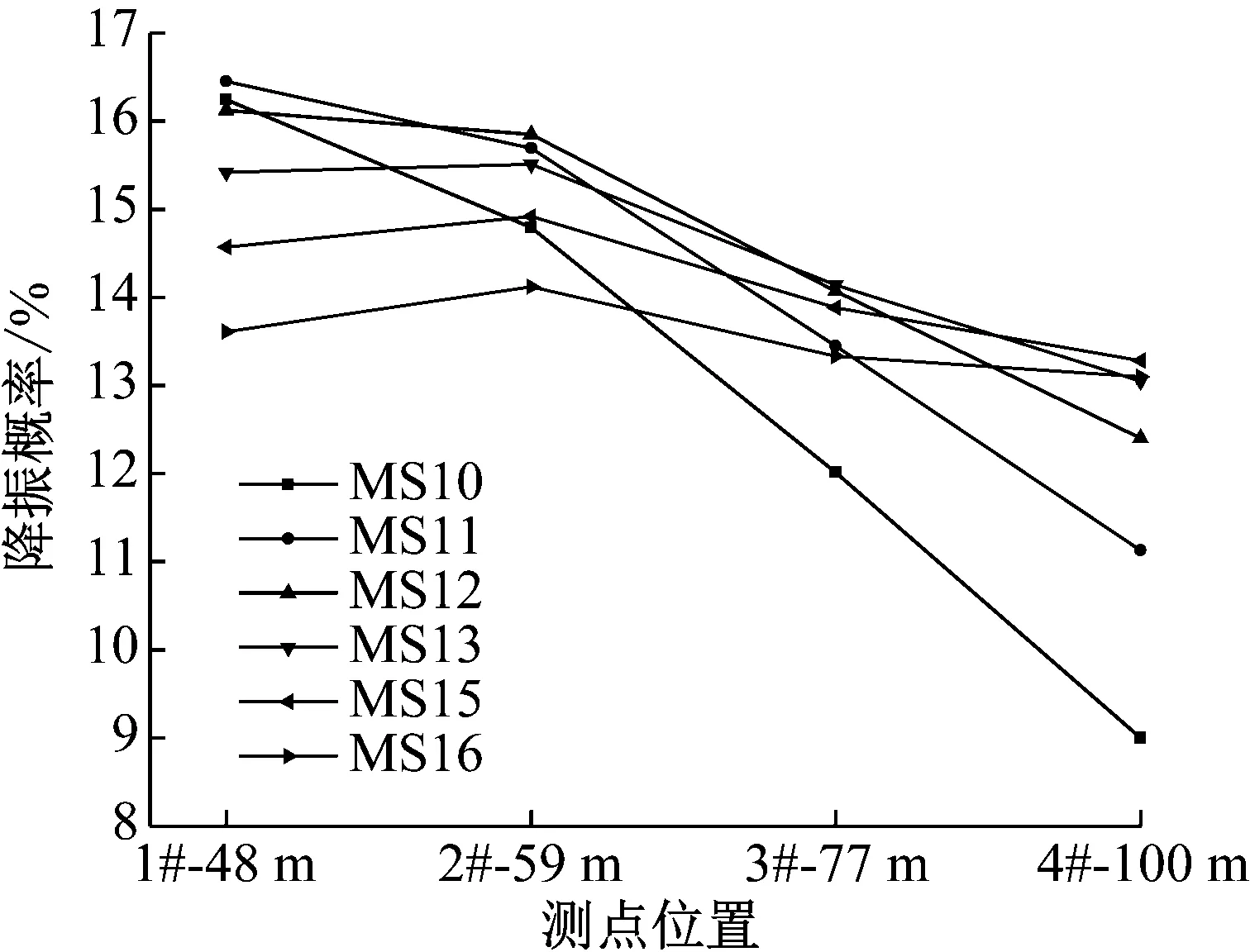
图7 不同测点处MS10～MS15雷管干扰降振概率

Fig.7 Interference reduction probability of MS10～MS15 detonator in different measuring points

4 结 论

(1) 叠加波形的降振率随微差时间连续变化。随传播距离的增加，最大降振率所对应的微差时间逐渐增大，局部最大降振率出现了多峰值的现象，降振率逐渐降低。

(2) 以叠加波形的振速幅值为标准，分析得到不同距离测点处的最优微差时间：48 m处为15～25 ms，59 m处为17～28 ms，77 m处为19～30 ms，100 m处为22～34 ms，155 m处为37 ms。

(3) 将雷管延期误差视作随机变量，利用数理统计方法，计算得到MS10～MS15段雷管的延期误差概率。

(4) 建立概率模型，计算出因炮孔延期误差而引起的干扰降振的概率值。对比得到：近距离测点，低段位雷管的降振概率较大，远距离测点，高段位雷管的降振概率较大；此外，低段位雷管的降振概率受测点距离影响较大，高段位雷管所受影响较小。