淹没条件对连续射流破碎含瓦斯煤效率影响研究*

杨腾龙，王兆丰,2，陈金生，王 龙

(1.河南理工大学 安全科学与工程学院，河南 焦作 454000；2.煤矿灾害预防与抢险救灾教育部工程研究中心，河南 焦作 454000)

0 引言

水射流研究始于20世纪，在石油、矿业和建筑工程等领域都有着广泛的应用[1-3]，显示出了巨大的发展潜力。水力冲孔[4]、水力割缝[5]等技术的应用即是建立在水射流理论研究基础之上，是目前公认的行之有效的煤层增透措施。但是这些措施在现场应用中，时常会出现淹没射流[6]条件，例如下向孔，钻孔中的积水受重力作用难以及时排出，导致射流过程处于完全的淹没状态。此外，还有上向孔和水平孔，水体会囤积于射流形成的下侧坑体内或者缝隙中，形成局部的淹没射流。淹没条件会削弱射流破煤的整体效率，封孔接抽后期会直接影响到瓦斯抽采效果，在布孔参数不合理的条件下甚至会出现抽采空白带。因此，对比分析非淹没射流及淹没射流在破煤效率上的差异、精确把握淹没条件对射流破煤效率的削弱程度，对煤矿井下安全、高效地使用水射流技术具有重要的指导意义。

王宗龙等[7]利用超高压射流数控切割平台，进行了淹没条件下切割花岗岩的实验，探索射流参数对切深的影响，并运用回归分析法得到淹没状态下磨料射流切割岩石的半经验参数模型；康旭[8]在实验室条件下进行正交实验，研究分析了不同切割参数对淹没式磨料水射流切割能力的影响；廖华林等[9]采用超高压射流数控自动万能切割机进行了淹没状态下超高压水射流切割破岩试验，证明超高压水射流破岩存在最优喷距及喷射角度；王瑞和等[10]通过自主搭建的实验平台，对淹没状态不同射流参数下磨料射流切割套管的深度进行对比分析，并建立了工程计算模型，为石油领域磨料射流切割套管的工程应用提供了理论支撑。前人在实验室方面做了大量试验研究，取得了较为丰硕的研究成果，但基于目前技术条件的限制，想要在射流破煤的瞬间，几乎是毫秒量级的时间内观测到煤体的破碎过程及应力演化规律难度极大。因此，借助计算机数值模拟软件的“眼睛”，观测煤岩体的瞬时破碎过程，以往研究学者也做了大量工作。司鹄等[11]、刘佳亮等[12]、张宏[13]对淹没射流不同射流参数下的破岩过程进行模拟，探讨不同冲击速度下应力波在岩石中的传播和衰减过程，得到了岩石在水射流作用下的破碎损伤演化、应力波传递、岩石破碎过程中流体与固体的相互作用等动态扩展过程；高激飞等[14]采用PHOENICS商业软件，模拟计算了深水水域淹没磨料射流流场的分布特征，模拟得出淹没条件下固液两相射流的速度与压力分布规律。

前人数值模拟方面的研究大多是从破碎岩石角度出发，然而煤体相对于岩石，其内部本身会蕴含一定压力且具有自喷性的瓦斯气体，会对整体射流破煤效率产生一定程度的影响。因此，破岩模拟难以较为真实地模拟井下破煤过程。另外，以往数值模拟中没有对非淹没射流及淹没射流下破煤效率的差异进行系统性的对比研究，缺乏对两者破煤效率差异性的定量考察。基于此，笔者拟借助Ansys/Ls-dyna模拟软件，建立围压状态下非淹没及淹没射流破碎含瓦斯煤体流固耦合模型，全面展示非淹没射流及淹没射流破煤详细的物理过程和相关力学信息，并通过对比相同时间下淹没射流与非淹没射流破煤深度的差异，探究淹没条件对射流破煤效率的削弱程度，以期为煤矿井下安全、高效地使用水射流技术提供参考。

1 数值模拟

1.1 模拟软件介绍

Ansys/Ls-dyna是目前通用的1种显式动力分析程序，包括Lagrange、ALE和Euler这3种算法，软件内置多种单元库、材料本构模型以及多种气体状态方程，除此之外，还提供了50余种接触方式，适用于分析高速碰撞、侵蚀穿透等问题。ALE 算法的优点是计算网格不依附于流体质点，而是可以相对于坐标系做任意运动。这种描述既包含了Lagrange观点，可应用于带自由液面的流动，也保留了Euler观点，克服了纯Lagrange方法常见的网格畸变的弊端。目前，ALE算法已被广泛用来研究带自由液面的流体晃动问题、固体材料的大变形问题、流固耦合等问题。

1.2 模型建立

非淹没射流及淹没射流三维模型如图1所示。模型参数见表1。

图1 非淹没射流及淹没射流三维模型Fig.1 Establishment of 3D model of non-submerged jet and submerged jet

1.3 边界条件设定

模型为1/4模型，因此在YOZ对称界面上限制其X轴的平动以及Y轴和Z轴的转动；在XOY对称界面上限制其Z轴的平动以及X轴和Y轴的转动；对底面采取ALL DOF全约束，限制底面移动。同时对煤体、水域和瓦斯域的各个面施加无反射边界条件，以模拟空间无限大区域。

表1 模型参数设置Table 1 Model parameter setting

1.4 力学模型

1)连续性方程：

(1)

2)动量方程：

(2)

式中：σij为应力张量，其方程表述为：

σij=-Pδij+μ(vi,j+vj,i)

(3)

3)能量方程：

(4)

式中：ρ为介质密度，kg/m3；xj为欧拉坐标，m；t为时间，s；bi为体力，N；vi为物质速度，m/s；wj为相对速度，m/s；μ为动力黏性系数，N·s/m2；P为压力，Pa；δij为Kronecker函数；E为内能密度，J/m3。

4)煤体本构方程：

由于水射流破煤问题属于大变形、高应变率、非线性的撞击问题，因此选取能较好模拟大应变、高应变率及高压效应下的H-J-C模型作为煤体的本构模型，其规范化等效应力描述如下：

(5)

(6)

式中：Δεp是等效塑性应变增量，无量纲；Δμp是等效体积应变增量，无量纲；D1(P*+T*)D2为常压P下材料断裂时的塑性应变，无量纲；T*为最大拉伸静水压力，MPa；D1与D2为损伤常数。

5)瓦斯和水的本构方程：

瓦斯和水的本构方程用Gruneisen状态方程表示，当材料受压时表示为：

(γ0+αμ)E

(7)

式中：ρ0代表初始密度，kg/m3；C是μs与μp关系曲线的截距，m/s；μs为冲击波速度，m/s；μp为质点速度，m/s；E为单位体积内能，J/m3； S1，S2和S3是常数；γ0是Gruneisen系数；α为泊松比，是对γ0的一阶体积修正。

μs与μp可通过下式进行相关联：

(8)

1.5 模型材料参数

1.5.1 煤体模型

考虑到淹没射流条件下水的润湿会在很大程度上改变煤体的力学性质，对煤体本身起到了“软化作用”，因此，需依据现场实测对煤体材料进行赋值。通过Section_Solid定义ELFORM为1，即持续应力固体单元，通过Non_Reflecting设置无反射边界后用Define_Curve定义4 MPa的恒定压力时间曲线，然后通过关键字Load_Segment_Set调用此圧力曲线后施加于煤体各个面的节点上，以此建立了围压为4 MPa的煤体模型。为确定煤体去除准则保证其正常破碎侵蚀，需要给煤体模型增加侵蚀关键字Mat_Add_Erosion材料，将该材料设定为与煤体相同的材料编号，考虑到松软煤体具有较强的塑性软化流变特性，模型中以最大破坏应力为主要准则。当煤体单元累计受力达到其最大破坏应力时发生侵蚀，材料中定义等效破坏应力SIGVM数值为14 MPa，受力超过该数值单元就会立即失效并删除。

1.5.2 瓦斯域模型

瓦斯气体采用Mat_Null材料模型，然后通过Section_Solid定义ELFORM为11，即ALE多物质单元，设置无反射边界后，参照以上煤体围压设置方法给瓦斯气体施加1 MPa的压力。

1.5.3 水域及水射流模型

水域和水射流同样采用Mat_Null材料模型，通过Section_Solid定义ELFORM为11，即ALE多物质单元，然后定义Constrained_Lagrange_In_Solid中关键字CTYPE为5，即罚函数耦合同时允许侵入煤体单元，这样保证射流先与水域中的水体耦合，然后共同作用冲击煤体。

材料参数设置见表2～4。

表2 煤体材料参数Table 2 The material parameters of coal

表3 瓦斯域材料参数Table 3 The material parameters of gas

表4 水射流和水域材料参数

2 结果分析

2.1 非淹没射流破煤结果分析

对非淹没射流1/4模型进行对称处理得到其1/2模型，并对非淹没射流破煤过程中水的射流状态及坑体破碎情况进行局部放大，以此更为清楚地动态追踪坑体单元的失效演化过程，结果如图2所示。

非淹没射流条件下，形成的破煤坑体截面与射流体本身的截面相差不大，上部径向截面稍大于下部截面，且煤体破碎形状较为规则，几乎成柱状向下延伸，这是因为水射流离开喷嘴后与瓦斯气体进行耦合然后作用于煤体，全程不考虑破碎煤体单元的反射过程，定义煤

图2 非淹没射流破煤过程Fig.2 Process of breaking coal by non-submerged jet

体单元受力达到其最大破坏应力时立即失效删除，因此射流断面在射流沿程扩张程度不大。由于连续射流的作用，后续持续的能量供给作用于煤体，不断使之破碎，形成最终的破碎坑体。

图3为煤体的有效应力云图。由图3可以看出，非淹没射流在破煤过程中，煤体所受应力主要分布于射流体前端，集中度较高，断面较小，应力分布随坑体延伸逐渐下移，坑体壁上存在少量应力集中区，这是因为狭小的坑体空间相对于较大流量的高速射流水体，会引起局部排水受阻，在连续射流的作用下，水体回流过程产生了部分应力集中现象。

图3 非淹没射流破煤应力分布Fig.3 Stress distribution of coal bursting by non-submerged jet

再次对1/2模型进行对称处理得到图4所示的整个煤体模型，并以不同时刻下的射流破煤深度作为衡量破煤效率高低的指标，绘制不同速度下的破煤坑体演化时程曲线，如图5所示。

图4 非淹没射流不同速度下坑体形态Fig.4 Pit body morphologies at different jet velocities of non-submerged jet

图5 非淹没射流破煤深度与时间关系Fig.5 Relationship between breaking coal depth and time by non-submerged jet

由图5可以看出，非淹没射流条件下，破煤深度基本呈线性增长趋势，因为高速射流体在瓦斯气体介质中的速度衰减极为缓慢，且射流沿程距离较短，导致水射流破煤效率前后变化很小。对比不同速度下的破煤深度，可以发现不同速度下射流破煤从 1 000 μs开始显现出较大差异，且随时间稳步上升，射流速度越大，坑体越深，破煤效果越好，最终形成了如图6(b)所示的类似柱状的破碎坑体。将数值模拟得到的煤体破碎断面与实验[15]结果进行对比，对比结果如图6所示。数值模拟得到的煤体破碎口与实验条件下的破碎口形状较为一致，可以在一定程度上作为数值模型正确性的参考。

2.2 淹没射流破煤结果分析

对淹没射流1/4模型进行对称处理得到其1/2模型，如图7所示。由图7可以看出，淹没射流条件下，初始阶段形成漏斗状的破碎坑体，然后随着射流时间延长，逐渐向下延伸；随着破碎深度的增加，上层水域中的水体受自身的重力作用也流进坑体内，水域中的水在射流过程中也会向外排出。在此阶段，射流冲蚀煤体形成的破碎坑中会产生水垫作用，坑体深度增速放缓。另外，破煤坑体的直径明显大于射流直径。这是因为高速射流体会卷吸周围介质中的水，导致射流断面随之增大，破煤直径显著增加。实验[10]条件下的破碎坑体形状如图8所示。在破煤瞬间，数值模拟所得的坑体截面经局部放大后如图7(a)所示，与图8中实验[10]条件下破煤瞬间形成的坑体截面形状较为一致。

图8 淹没射流破碎断面形态Fig.8 The broken section of submerged jet

图9为煤体的有效应力变化云图。由图9可以看出，射流破煤过程中，射流体前端形成了较大截面的应力集中，可以明显看到射流体对周围水体的卷吸作用，导致截面扩大，作用于煤体后使煤体破碎，然后随坑体延伸逐渐下移。动态追踪不同射流速度下破碎坑体单元失效演化过程，得到坑体深度与时间关系曲线，如图10所示；淹没射流不同速度下的坑体形态如图11所示。

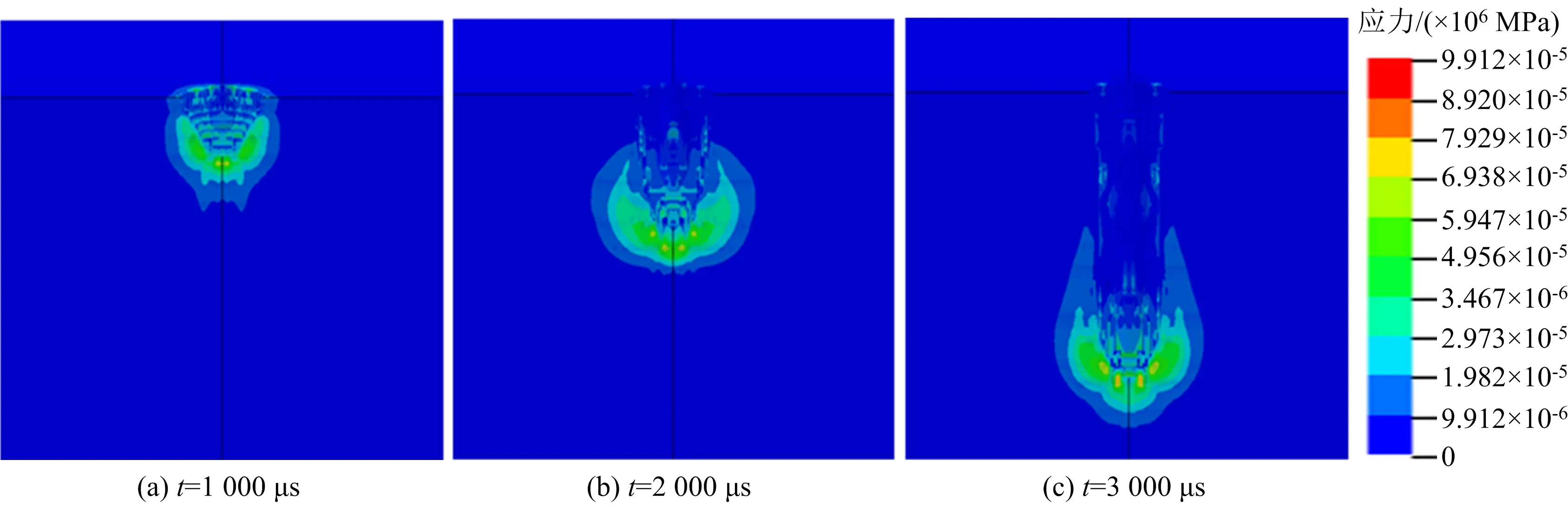
图9 不同时间淹没射流破煤应力分布Fig.9 Stress distribution of coal bursting by submerged jet

图10 淹没射流破煤深度与时间关系Fig.10 Relationship between breaking coal depth and time by submerged jet

图11 淹没射流不同速度下坑体形态Fig.11 Pit body morphologies at different jet velocities of submerged jet

由图10和图11可以看出，淹没水射流在极短时间内就可破碎煤体，在初始阶段0～100 μs内曲线斜率最大，破煤效率最高，而后破煤效率有所减慢。这是因为水射流从喷嘴喷出瞬间，能量最大，然后会与周围水域发生动量交换，速度逐渐降低，破煤能力逐渐减弱，起初由于较小的靶距相对于较高能量的射流体，对破煤效率的影响较小，然而随着冲蚀深度的增加，射流靶距也逐渐延长，从喷嘴喷出的水射流与水域中的水体动量交换时间加长，射流速度会有一定程度衰减，但由于连续射流的作用，射流水体具有持续的能量供给，作用于狭小的坑体空间内，衰减幅度并未太大。对比不同射流速度下的破煤效果，初始阶段0～100 μs未表现出明显差异，这一阶段破煤效率相差不大，而后随时间增长逐渐拉开差距，并各自呈稳步上升态势。

2.3 淹没射流、非淹没射流破煤效率对比分析

相同时间、不同速度下淹没射流及非淹没射流破煤坑体最终深度如图12所示。由图12可以发现，淹没射流平均破煤深度是非淹没射流平均破煤深度的41.46%。数值模拟结果表明，淹没射流条件会削弱整体破煤效率。因此，井下采用高压水射流技术时应充分考虑2种不同射流条件造成的破煤效率的差异。

图12 淹没射流与非淹没射流破煤深度关系Fig.12 The relationship between submerged jet breaking coal depth and non-submerged breaking coal depth

3 结论

1)非淹没射流破煤坑体断面较窄，深度较深，破碎坑体直径几乎等于射流直径，初始阶段及后期坑体发展阶段破碎效率相差不大，不同速度下破碎效率在1 000 μs后显现出较大差异。淹没射流破碎坑体破碎断面较宽，深度较浅，坑体直径明显大于射流直径，初始阶段破碎坑体呈漏斗状，0～100 μs破煤效率最高，而后坑体随时间延长逐渐向下延伸，破煤效率逐渐降低。

2)相同工况、同一时间内，淹没射流平均破煤深度是非淹没射流平均破煤深度的41.46%，淹没条件会在一定程度上削弱整体破煤效率，因此，井下采用高压水射流技术时应充分考虑2种不同射流条件造成的破煤效率的差异。

3)此项研究中，为更清晰地观测射流破煤的坑体深度及具体形态，数值模拟过程中定义煤体单元所受应力达到最大破坏应力时立即失效删除，因此忽略了破落下来的煤体单元的反射过程，在以后研究中可做进一步探讨。