减震孔在小间距隧道爆破开挖中的降振效应

，，，，，

(1.山东科技大学 山东省土木工程防灾减灾重点实验室，山东 青岛 266590；2.山东科技大学土木工程与建筑学院，山东 青岛 266590；3.日照市建筑设计研究院有限公司，山东 日照276800)

随着国民经济的快速发展，既有单线铁路运输能力已不能满足经济快速发展的需求。通过将原有单线铁路改增建为复线来对既有铁路进行改造，既可大大提高既有铁路的运输能力和运输效率，又可节省建设投资。然而，在复线修建的过程中，由于各种条件的限制，新建隧道与既有隧道相对间距可能非常小，导致新建隧道爆破开挖产生的爆炸应力波对原有隧道的结构安全产生重大影响。为了保证既有隧道不受爆破施工的影响，确保隧道的正常使用，在隧道掘进过程中需要严格控制爆破振动[1-4]。目前，控制爆破振动的措施主要是爆源控制和传播途径上的控制，其中开挖减震沟、设置减震孔和空孔是较为常见的控爆措施[5-8]。但开挖减震沟需要较大的施工空间，所以设置减震孔在控制爆破振动中更为常见[9-11]。大量的工程实例和研究成果证明设置减震孔可有效控制爆破振动强度。黎罡[12]利用Midas/GTS模拟工程爆破中减震孔的隔振效果，得到单排减震孔的减振率为10%～20%；惠峰等[13]通过数值模拟计算，分析了减震孔排数、空孔与爆源距离等减震孔布置参数对爆破地震波的衰减影响，对空孔的布置参数进行优化，提出在距离爆源1 m处打2排交错空孔的减振方案，减振效果明显；何兴贵等[14]通过现场试验对爆破振动速度进行监测，研究了减震孔附近爆破地震波传播变化规律，并设计孔径为90 cm的减震孔，当孔距为25 cm时，建议排距为40～75 cm。但均未给出减震孔布置具体最优位置和形式。

本研究拟通过数值模拟分析减震孔的孔间距、孔数、与爆源的距离以及与相邻隧道的距离对减振效果的影响规律，提出不同爆破条件下应采用的合理减震孔布置，不但可以达到预期的减振效果，而且能够减少施工成本，并利用萨道夫斯基高程修正公式拟合设置减震孔后的爆破振动衰减规律，为爆破工程减震设计提供借鉴。

1 减震孔的减振机理

减震孔的减振效果，即研究爆破应力波与减震孔的相互作用。如图1所示，将爆破应力波分成两部分，从减震孔底C点分开，把应力波粗略地分为两段，C点之上一段的爆破应力波视为减震孔底以上应力波，简称上部应力波。因为有减震孔的阻隔，爆破地震波在此处发生了反射和折射，能量会减少，进入保护区的能量较少，其振动速度较低，因此对保护区的破坏降低。另外C点之下一段应力波简称为底部应力波，当爆破地震波到达C点后发生能量分散，其中一部分以地震波的形式绕射进入保护区，进而引起保护区质点的振动，对保护区造成破坏。

图1 减震孔隔震示意图

根据不同布置形式下所得到的振动峰值速度，将对比前后项的振动峰值速度之差与对比前项的振动峰值速度的比值作为减振因子，减振因子的平均值为减振率η，将其作为减震孔减振效果的依据[15]。

(1)

式中：Vi前为对比前项爆破振动峰值速度；Vi后为对比后项爆破振动峰值速度。η值越大，表示减震孔减振效果越好。

2 爆破源-减震孔模型的数值模拟

2.1 模型参数

采用乳化炸药，药卷直径为32 mm，炮孔直径为40 mm，炮孔间距为500 mm，模拟炸药量为15.8 kg，装药方式为不耦合装药，模型材料和选择状态方程类型见表1。

表1 模型材料及状态方程

2.2 建立计算模型

为了缩短计算时间，建立了二维计算模型，模型尺寸40 m×40 m×0.01 cm。采用映射网格划分方法，为保证计算精度，最大网格单元尺寸为5 mm。对模型的Y轴方向进行约束，四周采用无反射边界条件。考虑掏槽爆破时爆破振动影响，掏槽眼布置在开挖隧道的中心位置，且监测点环绕布置在既有隧道。

为了研究减震孔的孔间距、孔数、与爆源距离的减振效果的影响规律以及既有隧道横断面振速分布规律，分别模拟了减震孔距离爆源0.3、0.5、1.0、1.5、2、2.5和3.0 m处设置间距为0.22 m的单排减震孔7种模型、未设置减震孔以及最优位置处设置不同布置形式双排减震孔的3种模型，共10种模型。对既有隧道靠近爆破掌子面的迎爆侧边墙、顶部、底板以及远离爆源一侧墙体设置监测的关键点，测点布置如图2所示，减震孔的孔径为90 mm，孔距为220 mm，排距为500 mm。图3为减震孔计算模型。

图2 模型尺寸及测点布置

图3 减震孔计算模型

3 数值模拟结果分析

3.1 有无减震孔振动速度云图对比分析

依照数值模拟计算结果，减震孔与爆源不同距离L的情况下，将既有隧道掌子面的横断面关键点振动峰值速度(表2)进行比较，分析减震孔对爆破地震波的衰减效应。

对未设置减震孔和设置单排减震孔、双排减震孔相同时间模型Mises等效应力云图进行对比分析(图4)。从图4(c)中可见，当地震波传播到减震孔附近时发生很明显的折射和绕射，有效地对地震波产生阻隔。单排减震孔时产生的阻隔范围和程度较小、能量衰减的效率低，双排减震孔加快了地震波的衰减，能起到更好的减振效果。

图4 模型Mises等效应力云图

测点质点峰值速度V/(cm/s)减震孔与爆源间距离L/m0.30.51.01.52.02.53.01 m(间距0.3 m双排减震孔)1 m(间距0.3 m双排梅花形减震孔)Vx12.7111.9811.4812.4611.9912.5112.519.469.261005Vz3.982.873.433.771.896.876.885.012.97V合12.7110.8313.4912.4812.0712.5212.5210.3310.16Vx9.659.328.6610.069.318.638.639.328.111006Vz3.353.505.103.131.855.815.995.833.47V合11.2810.8210.9112.4410.8310.4410.4410.839.74Vx8.428.308.569.348.318.498.488.308.341007Vz3.223.914.803.541.696.125.977.144.02V合11.2810.8611.7912.7410.8611.8111.8110.8610.36Vx10.9110.479.6410.5610.479.419.4111.9810.911008Vz3.393.085.085.101.965.866.525.501.92V合12.0311.3310.3512.1911.3311.5611.5612.0711.06Vx12.1212.1111.1411.0312.1112.1110.7811.1111.321009Vz3.832.784.024.571.887.317.433.282.31V合12.3312.3311.3211.2612.3312.8912.8910.3310.10Vx12.6211.8711.4612.5112.9912.6112.739.879.231010Vz3.912.952.533.972.896.276.585.082.99V合12.7311.9311.9112.6212.9712.7112.8210.6610.01

3.2 不同距离各测点振动峰值速度对比

为了比较不同距离时布置减震孔后各质点的振动特性，模拟了距离(L)为0.3、0.5、1.0、1.5、2、2.5和3.0 m时质点的振动峰值速度(表2)。图5为取质点1005、1006、1007、1008、1009的不同距离L时振动峰值速度。

从图5可以看到，质点峰值振动与减震孔距爆源距离(L)密切相关，但并非是线性关系。当减震孔距爆源距离小于1 m时，质点峰值X轴方向振动速度和合速度振动速度呈下降趋势，但质点峰值Z轴方向呈上升趋势。当减震孔距爆源距离大于1 m时，质点峰值振动速度呈上升趋势，减震孔距爆源距离大于3 m后，呈平稳趋势。可以看出，减震孔距离爆源1 m时，减震孔的衰减效率最高，随着距离的增加衰减效率降低；同一测点在相同的爆破条件下Vx>Vz，并且爆破破坏以近距为主，所以Vx可以作为爆破安全判断的依据。

图5 不同距离时质点振动峰值速度

3.3 相同距离不同布置形式各测点振动峰值速度对比

由图6～8可以看出，布置双排梅花形减震孔振动峰值速度明显小于其他布置形式，其中减震孔使Z方向振动峰值速度衰减效率最高。

根据公式(1)计算，在X方向的地震波传播中，双排梅花形减震孔比双排并列减震孔同地震波减振率高5.03%，双排梅花形减震孔比单排减震孔同方向地震波减振率高出4.82%，双排梅花形减震孔比无减震孔减振率高9.45%；在Z方向的地震波传播中，双排梅花形减震孔比无减震孔同方向地震波减振率高45.67%，双排梅花形减震孔比单排减震孔同方向地震波减振率高出33.27%；在合速度中，双排梅花形减震孔比无减震孔减振率高12.67%，双排梅花形减震孔比单排减震孔减振率高出9.75%，双排梅花形减震孔比双排并列减震孔减振率高出1.89%。

3.4 既有隧道横断面振动特性分析

从表2不同距离情况下质点振动峰值速度对比分析得出，既有隧道横断面的不同位置振动呈现一定的规律，在迎爆侧的墙体底板处和顶部振动峰值速度较大。图9既有隧道横断面不同位置振动峰值速度总体呈现为：迎爆侧的墙体底板处>顶部>背爆侧的墙体底板>两侧中墙。

在地震波的传播途径上，由于迎爆侧距离爆源最近，地震波通过岩石直接传播到达，然而既有隧道的顶部和背爆侧都已形成临空面，地震波的传播需要通过绕射才能到达顶部和背爆侧，因而损失了一定的能量。

图6 减震孔不同布置条件下X方向振动峰值速度对比

图7 减震孔不同布置条件下Z方向振动峰值速度对比

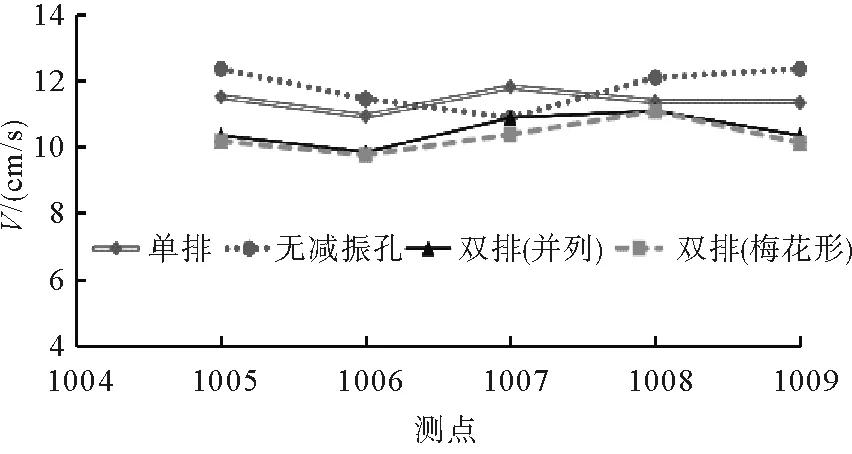
图8 减震孔不同布置条件下振动峰值速度对比

图9 既有隧道横断面不同位置振动峰值速度

4 回归数学模型

在隧道爆破参数设计以及施工过程中，提前对爆破产生的质点振动速度进行预测，对有效提高施工效率、避免因爆破施工对建(构)筑物破坏具有重要意义。

目前，国内外最常用的预测爆破质点振动速度的公式是萨道夫斯基经验公式，通过建立数学模型预测爆破振动的传播和衰减规律。实际上，爆破条件和地质条件等因素都会影响质点振动速度的峰值，其中测点与爆源高程差很容易被忽略。由于各测点之间高差大部分不在0.5～1.5 m，此时用常规的萨道夫斯基经验公式回归分析出的衰减指数和系数存在较大误差，为了提高预测精准度，利用高差影响改进回归数学模型，将萨道夫斯基公式[16]重新拟合为：

(2)

式中：V为质点振动速度；K为与介质和爆破方法有关的系数；Q为爆破单段最大装药量；L为爆源至测点的水平距离；H为爆源与测点之间的高程差；α为与岩性、地形地质等因素相关的地震波衰减指数；β为高差影响系数。

对既有隧道横断面设置各质点在不同爆破条件下测得数据统计分析见表2。利用最小二乘原理，对有减震孔的振动速度进行拟合得到：

5 结论

1) 小间距隧道爆破施工中，既有隧道迎爆侧的墙体底板处为振速峰值较高区，应作为重点监测部位，并将X方向峰值振动速度作为爆破安全评价标准较为合理，运用考虑高程效应的萨道夫斯基拟合公式，建立数学模型进行预测爆破振动的传播和衰减规律，确保既有隧道的正常运营。

2) 地震波传播过程中，随着减震孔与爆源距离L的增大，质点X方向峰值振动速度和质点峰值振动速度先减小后增大，而质点Z方向峰值振动速度相反，其中减震孔使Z方向(垂直方向)振动峰值速度衰减效率最高达到45%。

3) 减震孔直径为90 cm、孔间距为30 cm、排距为50 cm，相同爆破条件下，双排梅花形减震孔比单排减震孔减振率高出9.75%，双排梅花形减震孔比双排并列减震孔的减振率高1.89%。小间距隧道爆破施工中，设置双排梅花形减震孔减振效果更好。