《勾股定理的再发现》的探究教学
谭群燕

摘 要:在数学定理公式中,勾股定理属于重要内容。在教学期间需要确保学生能够深入了解和掌握勾股定理,以此提升学生的数学素养。在开展教学活动时可以通过探究活动和类比任务,对不同教学方案进行比较,以此提升数学教学效率和质量。通过实验结果能够看出,实验组班级的教学效果和学习效果明显优于对照组。实验组班级通过优化改进的教学方案,能够及时引导和启发学生,确保学生能够从第一个任务中获取学习经验,并将其应用到第二个任务中。通过自主探究的方式,能够加深学生对知识的理解和记忆。
关键词:勾股定理;教学实验
在平面几何中,勾股定理是重要定理,在初中数学教育教学活动中占据核心地位。在开展数学教学活动时,应当不断向学生渗透数学文化。通过勾股定理教学,仅仅可以使学生了解结论,并且在解题过程中套用,导致学生没有理解勾股定理。所以在新的教学方案中,应当引导学生不断思考和探究勾股定理,联合所学内容开展数学文化教学。
1 勾股定理的问题提出
我国初中数学教材中,关于勾股定理的呈现方式主要表现在以下方面:第一,命题法,通过直角三角形相似知识进行证明,常见于几何公理化教材中[1]。第二,测量法:指导学生测量直角三角形的三边长,以此验证勾股定理;第三,测量结论法:指导学生测量直角三角形的三边长,之后通过正方形面积计算法验证勾股定理。第四:在网格中计算正方形面积,明确正方形面积的关系,之后通过面积法验证。如课本教材引入。第五:指导学生应用全等三角形拼图,并且通过边长计算表示出面积的关系,这样能够通过运算法证实勾股定
理[2]。然而需要注意的是,以上不同方法在验证勾股定理时都存在不足问题,需要在后续教学中加以改正。下面以拼图为例,特别开展了一节《勾股定理再发现》的探究课。
2 教学方法改进,开展勾股定理再发现
几何学源于图案设计和土地测量,并且在古代几何学中比较注重研究面积问题。正方形面积属于简单的图形面积。所以在教学中可以设置不同的任务。第一,使用边长相等的正方形纸片,指导学生将其拼接为大的正方形。学生完成任务后总结反思,之后给予第二个任务,将不同大小的正方形纸片拼接为大的正方形。
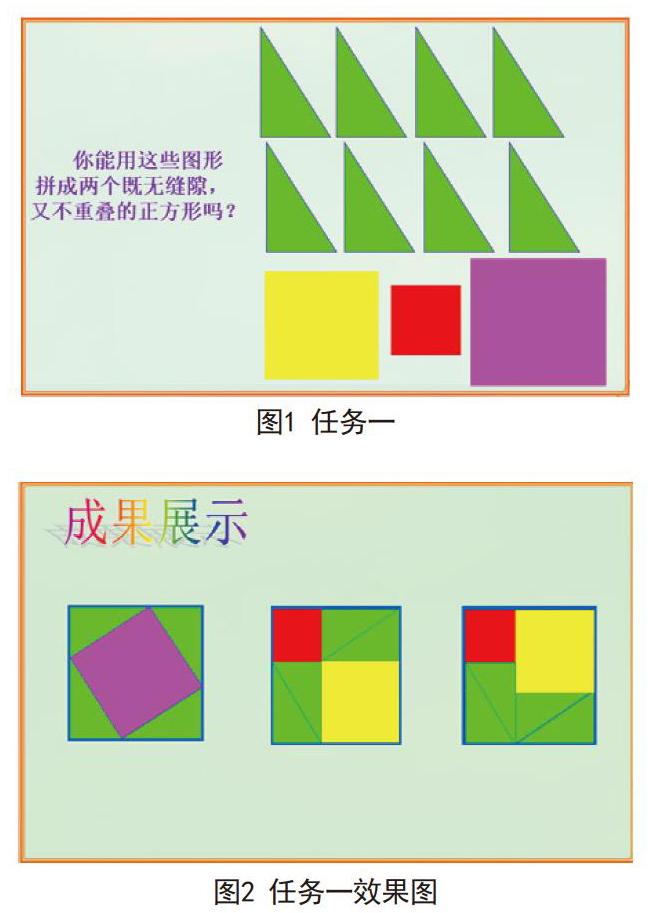
学生在完成第一个任务之后,探究操作过程能够为任务二提供参考价值。在第一个任务中,使用8个全等的直角三角形、3个以直角边的长度为边的正方形,如图1所示。学生在进行拼接之后,得到如图2的效果图。
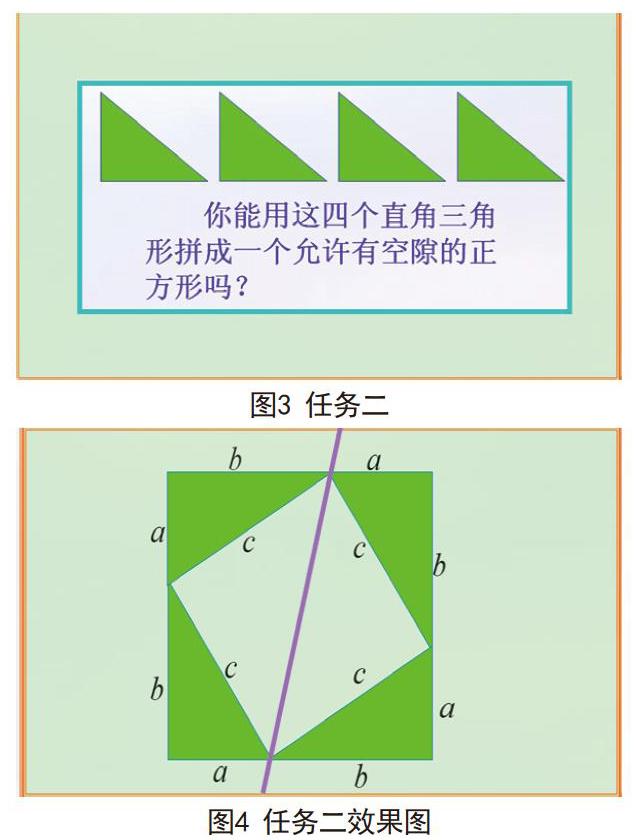
在开展第二个任务之前,学生应当与第一个任务进行比较,对两个任务的异同点进行比较。在教学期间,引导学生找到下面边沿的合适点,将其作为大正方形的邻边。这样能够明确两个正方形的下底边分割点。学生在完成任务之后,可以通过几何板展示出拼图过程,加深学生的印象。任务二主要是应用4个全等直角三角形拼接为一个大的正方形,如图3所示。学生在使用直角三角形拼接后,得到图4的效果图。
在完成上述任务之后,教师应当指导学生将面积与数量的关系转化为直角三角形的边长关系,使学生通过比较思维进行探索,以此发现出勾股定理的结论。在发现勾股定理之后,应当指导学生明确勾股定理的内容,并且介绍赵爽弦图和勾股定理的发现过程,并且对不同方法进行比较分[3]。通过此种方式,能够提升学生的乐趣感,确保其能够独立描述出勾股定理的证明过程。
3 教学比较实验过程
3.1 选择样本
选择某学校八年级三个班级的学生,使用专业统计学软件,对三个班级学生的不同学期的期末考试成绩进行t检验。通过检验比较结果能够看出,三个班级的期末考试成绩均大于0.05,无显著性差异,可以进行比较。检验结果如表1所示:
3.2 实验方案
将1班和2班作为实验组,3班作为对照组。实验组应用优化改进的教学方案,其中1班采用亲自施教法,2班采用教学观摩后,由任课教师带教。3班由任课教师自行教授。将整个实验过程录制为影像。在实验结束后,使用调查问卷对不同组学生进行调查。问卷内容包括:勾股定理是否为学生自己发现;写出勾股定理的验证过程,画出关键图像;此次调查所设计的问题,不仅能够使学生评价自己的发现感,明确学生是否为自己发现勾股定理;还能够使学生回顾勾股定理的发现过程,并且通过图形进行验证。
4 结果分析
4.1 实验过程
在此次实验中,学生花费6min完成第一个任务,使用3min总结方法;在开展第二个任务之前,教师进行引导分析,对两个任务的异同点进行比较。学生使用3min完成第二个任务,并且使用3min进行总结。在教学期间,学生能够独立完成拼图任务。
4.2 问卷调查结果分析
通过调查结果能够看出中,实验组班级学生自己发现勾股定理的占比为49%,能够自主回顾定理验证过程并书写正确的占比为38%;对照组班级则分别为14%和7%。通过对不同组别学生的数据进行t检验之后,通过分析结果能够看出,三个班级的赋分成绩均小于0.05,存在显著性差异。结果如表2所示:
通过比较分析结果能够看出,采用优化改进方案开展数学教学,能够使学生自主发现勾股定理,并且可以回顾验证过程和关键同型。
5 讨论
通过此次研究能够看出,实验组班级的教学效果和学习效果明显优于对照组。实验组班级通过优化改进的教学方案,能够及时引导和启发学生,确保学生能够从第一个任务中获取学习经验,并将其应用到第二个任务中。对照组班级在教学过程中,没有深度启发学习难点,导致学生在完成第一个任务时没有总结经验,因此影响了第二个任务的完成。所以应用优化改进的教学方法,可以改善教学效果,提升教学质量。
本文所提出的优化改进方案,具备以下优势特点:第一,赋予学生的任务比较简单。该操作过程在七年级已经实施过,因此学生具备操作经验。通过原有经验支撑,能够使学生从第一个任务过度到第二个任务中。在实际教学中,只有两个学习任务,能够明显减少课堂容量,给予学生充分的探索时间和思考时间。第二,不同任务之间存在关联性,在完成第一个任务之后,能够为第二个任务奠定良好基础,帮助学生积累相关经验。通过类比探究方法,能够使学生积累活动经验。第三,探索思维与证明过程具有连贯性,通过探索活动可以使学生开启验证思维,对勾股定理进行深入思考和分析。第四,在教学过程中,学生能够真正发现问题,并且通过自身所掌握的知识和经验,解决处理问题。通过自主探究的方式,能够加深学生对知識的理解和记忆。所以在勾股定理教学过程中,可以尝试应用本文所提出的教学方案,以此提升教学效率和质量。
参考文献
[1]陈锦喜,吴平生.初中数学解题课教学策略课例分析——以“勾股定理中的翻折问题”解题教学为例[J].中学数学研究(华南师范大学版),2019,22(20):23-25.
[2]吴增生,郑燕红,李宏彦,等.勾股定理教学实验研究——让学生真正经历勾股定理的“再发现”过程[J].数学教育学报,2017,26(01):50-54+75.
[3]张伟俊.初中数学探究式教学存在的问题与教学建议——以勾股定理教学现状的调查分析和教学改进为例[J].中国数学教育,2019,13(11):12-17.

