基于一维流动模型的高速列车隧道交会空气阻力数值模拟研究

贾永兴，李绵辉，梅元贵

(1.兰州交通大学 甘肃省轨道交通力学应用工程实验室, 甘肃 兰州 730070;2.兰州交通大学 机电工程学院, 甘肃 兰州 730070)

高速列车在明线运行时的空气阻力约占总阻力的80%，而在隧道内运行时的空气阻力在总阻力中的占比超过90%[1-2]。可见，高速列车在隧道内运行时的空气阻力问题是关系到牵引计算及隧道限坡的重要问题。

早在1926年，就出现了描述列车在明线运行时所受运行阻力的Davis公式，即R=C1+C2V+C3V2，其中C3V2项表示空气阻力。2003年颁布的欧盟标准EN14067-3给出了统一的列车运行阻力计算公式R=C1+C2V+TfC3V2(Tf≥1)，其中TfC3V2项表示空气阻力。该公式与Davis公式形式相同，只是额外增加了隧道因子Tf，Tf是列车在隧道内运行时空气阻力与列车在明线运行时空气阻力的比值。与明线运行时列车空气阻力基本恒定的特征不同，高速列车在隧道内交会时受到的空气阻力是一个时变过程，受车速、列车长度、车头形状、阻塞比、隧道长度、隧道结构、隧道壁面粗糙度及隧道内运行列车数量等因素影响[3]。而既有的研究多关注明线和隧道内单列车运行时的空气阻力，很少涉及隧道内列车交会空气阻力。

实车测试方面，PETERS[4]实测了ICE/V单列车通过Mublberg隧道时的空气阻力和Tf。赵有明等[5]采用隧道内特定有限区间惰行试验结合非恒定流模型，提出一种测定单列车通过隧道时附加空气阻力的方法。康熊[6]等提出了一种通过测试和分析求解高速列车明线运行空气阻力的方法。目前还未见到通过实车试验测试高速列车隧道内交会空气阻力的报道。实车试验还易受环境干扰，且试验只限于已建成的线路，组织困难，费用高昂。

模型实验方面，YANG[7]等给出了一种确定动模型列车通过隧道时空气阻力系数的方法。但由于缩尺比例及局部细节的过多简化，仍无法真实反映列车运行的真实情况。

三维数值模拟方面，CHU[8]等研究了中国台湾700T高速列车以300 km·h-1在长912 m隧道中央等速交会时的空气阻力；SUN[9]等研究了3辆编组CRH3列车在长度为390 m的隧道内交会时的空气阻力；HWANG[10]等研究了2辆编组和3辆编组KHST列车在隧道内交会时的空气阻力。但由于当时计算机硬件资源和计算时间的限制，研究成果多集中在短编组高速列车在较短隧道内交会时的空气阻力特征及形成机理方面。

理论分析计算方面，HARA[11]在计算列车隧道运行空气阻力时，忽略了隧道内空气压力波动和活塞风影响。SOCKEL[12]在计算隧道内空气压力变化幅值基础上，建立了列车完全驶入隧道后平均空气阻力的计算方法。王韦[13]等考虑了隧道内活塞风速的非恒定变化，建立了计算列车通过隧道时空气阻力的计算方法。但上述研究均只针对单列车通过隧道的空气阻力问题。

隧道压力波一维计算方法的发展[14-15]使得计算列车通过隧道的时变空气阻力成为可能。一维可压缩非定常不等熵流动模型[16-17]计算隧道压力波方面的应用已被工程设计认同，其精度和准确性相比以往的定密度有限声速非定常流动模型和可压缩非定常等熵流动模型均有较大改善。YAMAMOTC[18]，VARDY[19]及史宪明[20]等采用一维流动模型计算了单列车通过隧道时的空气阻力。史宪明[21]采用一维不可压缩流动模型研究了我国CRH3型动车组在隧道内交会及同向运行时的空气阻力。

中国标准动车组CR400AF外形与CRH380A型动车组相比有较大改变，加之目前我国高速铁路隧道多为双线隧道，本文采用一维可压缩非定常不等熵流动模型和广义黎曼变量特征线法，对2列中国标准动车组CR400AF在隧道内交会时空气阻力及其影响因素开展系统研究。

1 高速列车隧道交会压力波计算模型

高速列车在隧道内交会过程引起的空气流动是伴随有流动分离和传热的三维、非定常、可压缩湍流流动。通常情况，隧道长度远大于隧道横截面当量水力直径，因此，隧道内大部分区域的空气流动可简化为一维可压缩非定常流动。而列车端部和隧道洞口等处空气流动具有强烈的三维效应，可通过合理的边界条件进行处理。此外，与单列车通过隧道形成的单环形空间类似，2列列车隧道内交会过程形成的双环形空间横截面的当量水力直径仍远小于双环形空间的长度。该空间几何特征，使得空气压力变化波及整个断面的时间远小于其沿列车长度方向的传播时间。这也是采用一维流动模型进行隧道交会压力波数值模拟的基本依据。通过与国外实车试验数据的对比，一维流动模型计算高速列车隧道交会区域压力波动的误差≤8.5%[22]。

首先设定如下前提条件：隧道为等截面且不设置通风竖井、横通道等辅助结构的平直隧道；列车车厢绝对密封；隧道内的空气是理想气体。考虑空气与隧道壁面、列车表面之间的摩擦和传热，一维可压缩非定常不等熵流动模型(简称为一维流动模型)的控制方程[15]如下。

连续性方程：

(1)

动量方程：

(2)

能量方程：

(q-w+uG)ρ(κ-1)

(3)

式中：ρ，p，κ为空气的密度、压力、比热比；t为时间自变量；x为空间自变量；u为气流速度；c为当地音速；G为摩擦力项；q为空气与壁面传热项；w为列车壁面对空气所做的功。

限于篇幅，对G，q和w的表述方法不再赘述。在隧道进出口端及列车车头车尾端，需要额外建立边界条件。由于列车交会瞬间流动的复杂性，采用一维准定常定密度流动模型建立相向运行列车隧道交会过程的边界条件[15]。

通过上述控制方程及边界条件可求解隧道内空气的压力p、流速u和密度ρ随时间t和空间x的变化规律。控制方程式(1)—式(3)组成的一阶拟线性双曲型偏微分方程组，通常采用特征线法求解。求解时，首先将上述方程组转换为由u，p和ρ表示的特征方程；再将其转化为由广义黎曼变量λ和β以及表示空气质点熵值的量AA组成的方程后求解；最后将λ，β及AA转化为p，u和ρ[15]。

2 高速列车隧道交会空气阻力计算方法

计算高速列车隧道交会空气阻力时将列车在隧道内的交会过程分为2部分：第1部分为相交过程，自观测列车车头与对向列车车头相遇开始，直至其与对向列车车尾相遇为止；第2部分为分离过程，自观测列车车头与对向列车车尾相遇开始，直至观测列车车尾与对向列车车尾相遇为止。

建立2列车隧道交会过程中观测列车车头端和车尾端的流动控制体如图1所示。图中：车前空间车头处断面1—1、环形空间车头处断面2—2、环形空间车尾处断面3—3和车后空间车尾处断面4—4上的流动参数通过下角标1，2，3和4区分；列车交会期间xTR_Single为单列车时车壁面与隧道壁面形成的单环形空间的长度，xTR_Double为2列车时车壁面与隧道壁面形成的双环形空间的长度；u′为空气的相对流速，此时坐标系与观测列车同向等速运动；v为列车相对地面的运行速度；FN和FT分别为观测列车车头和车尾对空气的作用力。

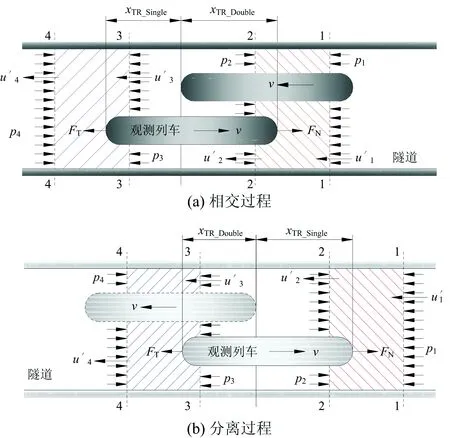
图1 2列车隧道交会过程的流动控制体示意图

2.1 空气阻力计算公式

在求得隧道内空气的压力p、流速u和密度ρ的基础上，可计算高速列车隧道交会空气阻力。

单列车通过隧道时空气阻力的计算公式详见文献[16]，此处不再赘述。列车在隧道内相交、分离2个过程中空气阻力的计算公式如式(4)和式(5)所示。式中：第1项与第2项之差为车头端压差阻力，第3项表示车头端到交会点车身受到的摩擦阻力(相交过程对应双环形空间，分离过程对应单环形空间)，第4项表示交会点到车尾端车身受到的摩擦阻力(相交过程对应单环形空间，分离过程对应双环形空间)，第5项与第6项之差为车尾端压差阻力。

1)相交过程

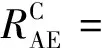
(4)

2)分离过程

(5)

2.2 验证

如前文所述，目前还未见到高速列车隧道交会空气阻力的实车实验结果。采用文献[8]2列车隧道中央等速交会数据和三维数值模拟结果，验证本文一维流动模型应用于高速列车隧道内交会空气阻力和压力波计算的合理性，结果如图2所示。可见，基于一维流动模型计算得到的空气阻力和压力波变化时程曲线，基本准确反映了列车在隧道中央等速交会时的空气阻力和隧道内压力波动变化规律；与文献[8]的数值模拟结果相比，本文计算的空气阻力的最大值和平均值误差分别为-1.53%和8.50%，可满足实际工程计算精度的要求。

图2 一维流动模型验证

3 高速列车隧道交会空气阻力时间历程特征

以高速铁路双线隧道为例，净空面积为100 m2；列车为中国标准动车组CR400AF，横截面面积为11.93 m2，8辆编组，运行速度350 km·h-1。列车从隧道两端同时进入隧道，运行速度相同，在隧道中央交会。

3.1 隧道长度为2 km时

采用本文提出的高速列车在隧道交会时的空气压力波动、空气阻力计算方法，计算得到的气流参数变化特性如图3(a)，(b)和(c)所示。图中：观测列车车尾在22.63 s时驶出隧道出口端，故横坐标取值到23 s；车头前风速在运动的列车坐标系中求解，其正方向为列车前进方向。

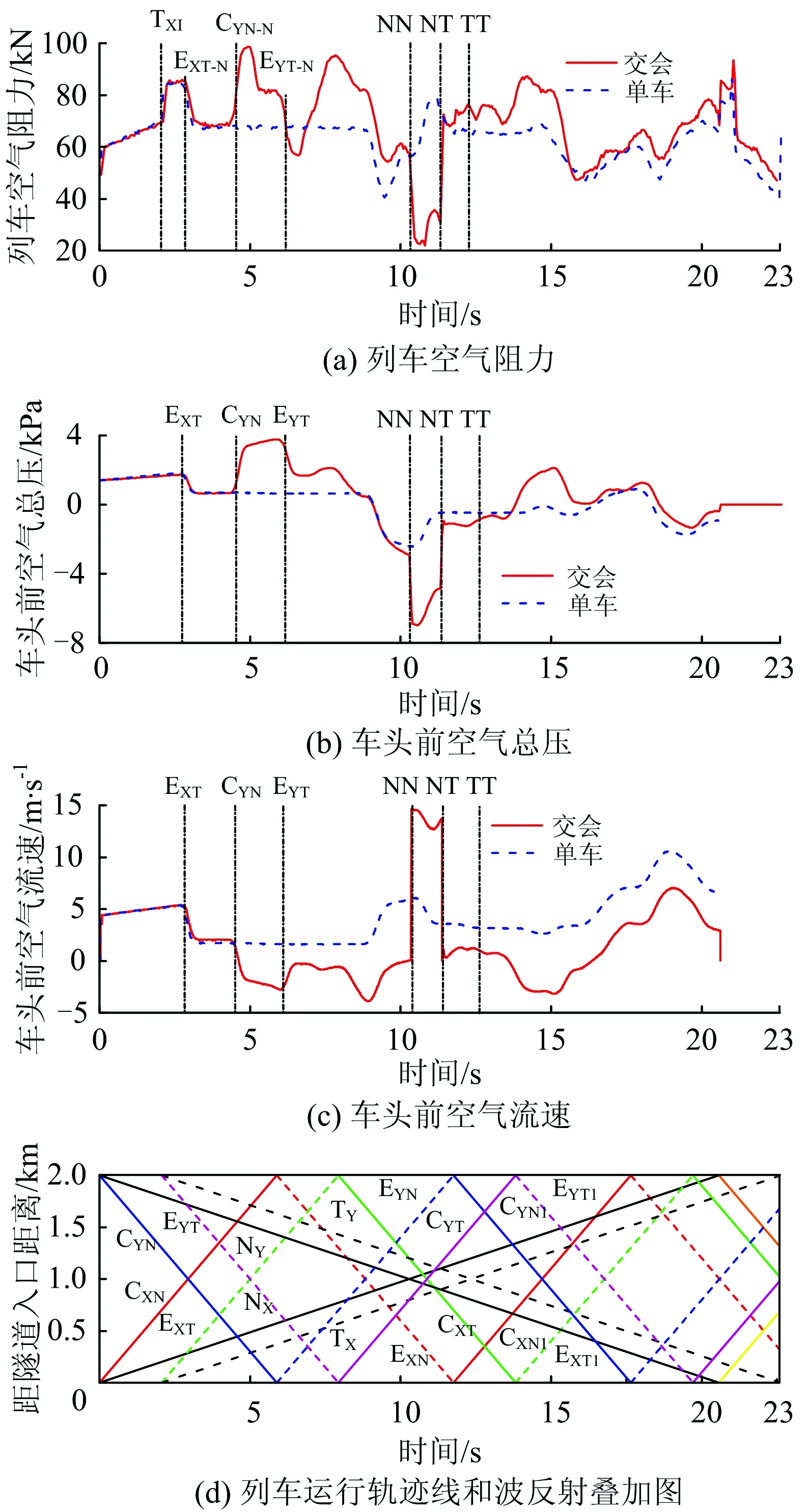
图3 列车空气阻力及气流参数变化规律与隧道交会时列车运行轨迹和波反射叠加图

图3(d)中对应给出了列车运行轨迹线和压缩波膨胀波的反射叠加图。图中：黑色粗实线和黑色粗虚线分别表示列车车头和车尾运行轨迹，N和T分别表示车头和车尾；细实线和细虚线分别表示压缩波和膨胀波的传播轨迹，C和E分别表示压缩波和膨胀波，并以不同颜色区分不同的波系，红色线和蓝色线线族表示车头驶入隧道诱发的波系，绿色线和粉色线线族表示车尾驶入隧道诱发的波系，橙色线和黄色线线族表示车头驶出隧道诱发的波系；下角标I和O分别表示列车驶入和驶出隧道端口；下角标X和Y分别表示观测列车和对向列车。

图3(a)为区别压缩波和膨胀波对车头端和车尾端压差阻力的影响，在下角标“-”后加入N或者T，表示压缩波或膨胀波与车头或车尾相遇；下角标I表示车尾驶入隧道瞬间。

从图3可知，隧道交会时列车空气阻力、压力及风速变化均比单列车通过隧道时剧烈，尤其2列车交会前后的气流参数变化更加剧烈。针对观测列车，详细分析如下。

1)阶段1：观测列车驶入隧道过程(0～2.06 s)。

(1) 观测列车车头驶入隧道瞬间，由于隧道壁面和列车壁面限制，车头前方空气累积受压，总压升高；同时，车头前空气受到挤压加速向前运动，风速急剧增大，气流方向与列车运行方向相同；列车空气阻力急剧增大，比明线运行时增大约10 kN。

(2) 随着观测列车车身逐渐进入隧道，车头前空气总压近似线性缓慢增大，车前空气受挤压继续向前运动；列车空气阻力缓慢近似线性增大。

(3) 在观测列车车尾驶入隧道，形成膨胀波的TXI时刻(t=2.06 s)，车尾附近形成强烈负压区，列车空气阻力再次急剧增大，比之前增大约10 kN。

2)阶段2：观测列车继续前行，且未受对向列车驶入隧道引起的压力波动影响之前(2.06～4.58 s)。

(1)随着观测列车继续驶入隧道，由于车尾负压效应逐渐增强，列车空气阻力仍逐渐增大。

(2)在观测列车车尾驶入隧道诱发的膨胀波传播至车头的EXT-N时刻(t=2.88 s)，与列车同向传播的膨胀波传播到车头时使得车头前方空气有向列车运行反方向流动的趋势(之前车头前方空气受到运动列车挤压，空气流动方向与列车运行方向相同)。此时，列车空气阻力达到最大值，约为98.56 kN。EXT-N时刻与TXI时刻相比，列车空气阻力增大约3.8 kN；随后，列车空气阻力急剧下降。

(3)CYN-N时刻之前，对向列车车头驶入隧道诱发的压缩波还未影响到观测列车。故而，观测列车的车头前空气总压、空气流速以及空气阻力变化规律与单列车通过隧道情形完全一致。

3)阶段3：观测列车开始受对向列车压力波动影响到列车交会前(4.58～10.29 s)。

自时刻CYN-N到时刻EYT-N的过程，即自观测列车车头遇到对向列车车头驶入隧道诱发压缩波的时刻至其遇到对向列车车尾驶入隧道诱发膨胀波的时刻为止的过程。这一过程中，压缩波和膨胀波与车头相遇对气流参数影响不同，车头前总压、车前气流大小和方向以及空气阻力的变化详见表 1。表中“波的传播方向”栏中“相反/相同”指压缩波或膨胀波传播方向与列车运行方向相反/相同，“车前气流”栏中“相同/相反”指压缩波或膨胀波导致气流的流动方向与列车运行方向相同/相反。

表1 空气阻力与车头前总压和气流变化间的关系

由表1可知：压缩波传播到车头时，不论与列车运行方向相同还是相反，均使列车空气阻力增大；而膨胀波传播到车头时，均使列车空气阻力减小。而压缩波和膨胀波传播到车尾时，其对车尾静压、车尾气流大小和方向的影响与对车头前的影响完全一致。压缩波和膨胀波传播到车尾时，其对列车空气阻力的影响与其传播到车头时正好相反。

随后的各时间阶段内，压缩波或膨胀波传播到车头或车尾时，车头前总压、车尾后静压以及车前和车后气流流速和列车空气阻力的变化规律均可参照表1进行分析。

4)阶段4：交会过程(10.29～12.34 s)。

(1)在观测列车车头与对向列车车头相遇的NN时刻，观测列车开始驶入对向列车车身周围的负压区，使得观测列车车头前空气总压急剧降低，列车空气阻力急剧减小。对向列车车身周围的负压区同样加剧了观测列车车头前方空气的流动。

(2)在观测列车车头与对向列车车尾相遇的NT时刻，观测列车车头驶出对向列车车身周围的负压区，观测列车车前空气总压和列车空气阻力均急剧增大。气流速度恢复到列车交会前状态。

5)阶段5：交会后到观测列车开始驶出隧道前(12.34～20.57 s)。

(1)观测列车车头与对向列车诱发的压缩波对向相遇的CYN1时刻，列车空气阻力急剧增大；观测列车车头与对向列车诱发的膨胀波对向相遇的EYT1时刻，列车空气阻力急剧降低。

(2)EYT1时刻后，列车空气阻力与单列车通过时列车空气阻力时程曲线基本重合，这是由于该时刻后，观测列车已经不受对向列车的影响。

6)阶段6：观测列车驶出隧道过程(20.57～22.63 s)。

(1)观测列车车头驶出隧道时，列车空气阻力反而有小幅上升。这可能是由于列车车头驶出隧道前，膨胀波使隧道出口端附近空气压力降低到小于隧道外大气压力水平所致。

(2)观测列车车头驶出隧道诱发的压缩波向隧道内传播与观测列车车尾相遇时，车尾负压度减小，列车空气阻力减小。

(3)随着观测列车车身逐渐驶出隧道，列车空气阻力逐渐近似线性地减小到明线运行时的数值。该过程与0～TXI时间段列车空气阻力线性增大过程刚好相反。

3.2 隧道长度分别为1和10 km时

目前还未见到研究隧道长度为3 km以上列车交会空气阻力的报道。为此，采用本文方法，其他条件不变，分别计算隧道长度为1和10 km时的列车空气阻力，如图4(a)所示。图4(b)和(c)中分别给出列车通过1 km隧道和10 km隧道时列车运行轨迹和波反射叠加图。

将图4与图3对比发现：列车在1 km隧道内交会时的列车空气阻力整体波动更剧烈，这是因为1 km隧道内的压缩波和膨胀波相比2和10 km隧道情况更频繁地影响列车车头或车尾；隧道长度为1 km时最大列车空气阻力达到115.6 kN，显著大于10 km时的93.0 kN；而10 km隧道内交会时的平均列车空气阻力(列车隧道运行过程中的空气阻力取时间平均)仅比1 km时略有增大，分别为69.7和67.0 kN。因此，在涉及牵引计算问题时，需要关注长隧道尤其特长隧道交会时的平均列车空气阻力；而涉及隧道限坡问题时，需要关注短隧道内交会时出现的最大列车空气阻力。

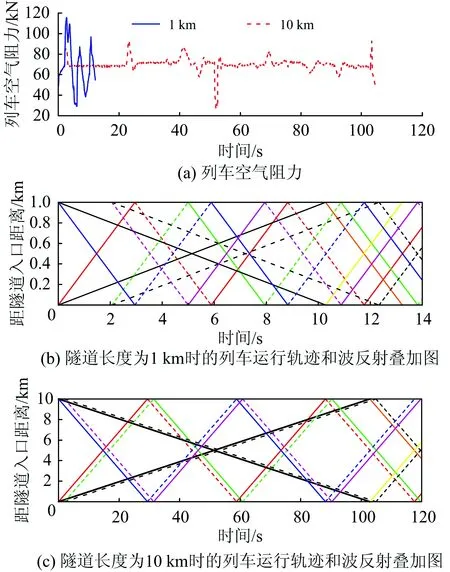
图4 隧道长度为1和10 km时列车空气阻力、列车运行轨迹和波反射叠加图

4 列车空气阻力主要影响因素分析

仍以前文给出的隧道和列车参数进行计算分析。影响高速列车隧道交会空气阻力的参数主要有：交会位置、隧道长度、阻塞比、车速和列车长度。以平均列车空气阻力RAVG、最大列车空气阻力RMAX和隧道因子Tf_AVG这3个指标研究列车隧道内交会的空气阻力。

4.1 交会位置的影响

隧道长度取10 km， 在隧道中央、距隧道出口1/3位置和隧道端口(距隧道出口150 m处)等速交会时的列车空气阻力时程曲线如图5所示。设观测列车在t=0 s时驶入隧道，对应隧道中央、距隧道出口1/3和隧道端口这3个交会位置，对向列车驶入隧道的时刻分别为t=0, 34.29和 99.77 s。为对比方便，图5(b)中对向列车空气阻力时程曲线以对向列车驶入隧道瞬间开始。

由图5可知：交会位置不同时，列车隧道交会的空气阻力时程曲线显著不同；前22.87 s内观测列车的空气阻力变化规律完全一致；22.87 s后，对向列车车头驶入隧道诱发的压缩波传播到观测列车车头时，观测列车的空气阻力变化出现差异；距隧道出口1/3位置和隧道端口位置交会时，对向列车空气阻力变化规律更复杂，且阻力值有所增大，如图5(b)0～10 s区间，这是由于对向列车驶入隧道前，观测列车的运动已对隧道内空气运动造成影响。

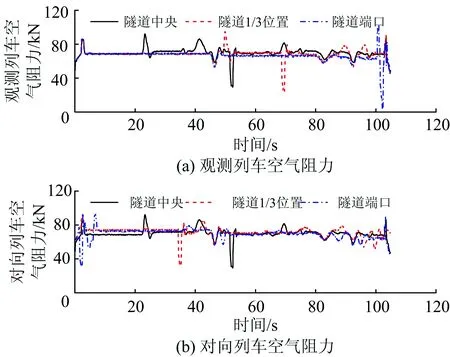
图5 交会位置对列车空气阻力的影响

按隧道中央、距出口1/3和端口3个交会位置次序，观测列车的平均空气阻力依次为69.74，68.23和66.31 kN；而对向列车的平均空气阻力依次为69.74，69.06和69.50 kN。可见，交会位置不同时，虽然列车空气阻力时程曲线显著不同，但平均列车空气阻力基本不变。

对于其它长度的隧道，计算结果显示，交会位置对平均列车空气阻力的影响类似。故以下均以隧道中央位置等速交会工况开展研究。

4.2 隧道长度的影响

列车编组取16辆，运行速度取我国高速铁路常采见的最高运营速度300和350 km·h-1，隧道长度LTU取1，1.5，2，2.5，3，4，5，6，7，8，9，10，15，20，25，30，35，40，45，50 km。需要说明的是，通常大于10 km的隧道采用双洞单线型式，但鉴于日本新干线26 km的八甲田隧道仍采用单洞双线型式，故本文将单洞双线型式隧道的计算长度扩展到50 km。隧道长度LTU对RAVG，RMAX和Tf_AVG的影响如图6所示。

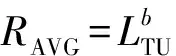
图6 隧道长度对列车空气阻力的影响

4.3 阻塞比的影响

阻塞比β取0.12，0.13和0.15，列车编组取16辆，运行速度取350 km·h-1，隧道长度取3，5，10和20 km，隧道中央等速交会时阻塞比β对RAVG，RMAX和Tf_AVG的影响如图7所示。

由图7可知：RAVG，RMAX和Tf_AVG均随阻塞比β的增大而增大；阻塞比越大，即隧道净空面积越小时，隧道长度对平均列车空气阻力的影响越大。因此，大阻塞比情况下，需要更加重视列车空气阻力的变化情况；采用方程RAVG=αβb进行数据拟合可得，隧道长度3～20 km时，b≈0.67～0.75，即RAVG与阻塞比的0.67～0.75次方成正比。

图7 阻塞比对列车空气阻力的影响

4.4 车速的影响

列车运行速度取200，250，300，350，400，450和500 km·h-1，列车编组取16辆，隧道长度取10 km，2列高速列车在隧道中央等速交会时车速对RAVG，RMAX和Tf_AVG的影响规律如图8所示。由图8可知：Tf_AVG基本不随车速变化而变化；RAVG和RMAX均随车速增大而增大；采用方程RAVG=aVb进行数据拟合可得b≈2，即平均列车空气阻力与列车运行速度的约2次方成正比。

4.5 列车长度的影响

列车长度取200和400 m，即常见的8辆和16辆编组，列车运行速度取300，350和400 km·h-1，隧道长度取50 km。定义空气阻力比值R16/R8为16辆编组高速列车平均空气阻力与8辆编组的比值。则列车在隧道中央等速交会时隧道长度对空气阻力比值R16/R8的影响规律如图9所示，可见，列车以300～400 km·h-1隧道内交会时，16辆编组高速列车的RAVG约为8辆编组的1.65～1.70倍。

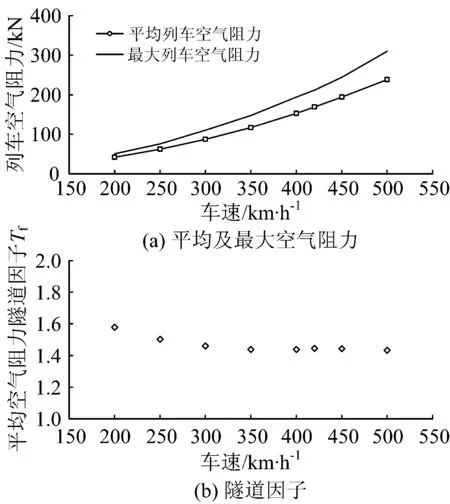
图8 车速对列车空气阻力的影响

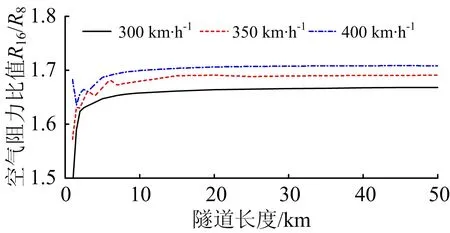
图9 列车长度对列车空气阻力的影响

5 结 论

(1)基于一维可压缩非定常不等熵流动模型和广义黎曼变量特征线法，考虑列车交会诱发的空气压力和流速耦合影响，提出了高速列车隧道交会列车空气阻力计算方法，计算误差不超过8.5%，满足工程计算要求。该方法尤其适用于长大隧道。

(2)高速列车隧道交会空气阻力与压缩波和膨胀波在隧道内传播叠加引起的车身附近压力和气流流速变化规律密切相关。

(3)在隧道中央等速交会时高速列车空气阻力随隧道长度、阻塞比和车速增大而增大。按影响程度由大到小排列依次为车速、阻塞比和隧道长度。交会位置对平均列车空气阻力的影响较小。计算结果显示，在隧道中央等速交会的平均列车空气阻力近似与车速的2次方成正比，与阻塞比的0.67～0.75次方成正比，与隧道长度的0.01次方成正比。时速300～400 km等级16辆编组高速列车在隧道中央等速交会的平均列车空气阻力约为8辆编组的1.65～1.70倍。