层次分析法在企业权重管理中的应用研究

李 玲

(中铁一局集团有限公司广州分公司，广东 广州 511400)

在传统的企业管理中，绩效管理、业绩考核中往往涉及考核指标的权重设置。目前企业对于考核指标的权重设计往往基于主要决策者的经验式管理得出，主观性较大，制定过程也不够透明，往往不能科学反映各指标的实际占比。由此制定的企业绩效考核办法有时在企业内部有较多反对声音，激励效果明显打折扣，在很多政府机关的绩效考核中已被淘汰。因此，在企业管理工作中，应用新的工具和方法，探索可量化、可测量的权重制定办法，提高权重因子制定的科学性，已成为提升企业管理水平和管理效率的必由之路。

层次分析法(Analytic Hierarchy Process，AHP) 是由美国的Thomas L. Saaty 教授于1987 年提出的一种科学分析方法。它与传统的定性分析方法不同，更多的基于定性分析与定量分析耦合，可将以往的基于决策者经验的决策过程转化为可量化、可测量的决策过程，进而实现企业决策水平的优化和提升。

文章拟应用层次分析法，探索在企业权重管理中更科学的制定方法，使得权重制定的过程更透明、可测量，符合企业的发展和激励机制的需要。

1 理论概述

层次分析法是将与决策过程相联系的关联因子分解成不同层次的子因子，并分析各层次的子因子的相关影响程度，根据各因子的影响程度不同，运用数学工具，进行定性分析和定量耦合分析的决策方法。

运用层次分析法解决问题的分析思路、决策过程与人类大脑对多维度问题的决策判断过程极其相似。以购买手机为例: 假如有5 款手机型号A、B、C、D、E 供选择，购买者会根据诸如品牌、操作系统、手机性能、摄像效果、内存大小和价格等一些考虑因素或因子去比选这5 款候选手机。首先会考虑这些影响因素或因子在心中的占比。比如追求品牌、不在乎价格，当然会首先考虑品牌，而注重性价比或仅需要基本功能的人则会重点考虑价格因素; 如果是一个摄影爱好者，则多会注重手机的摄像效果等。然后，就每一个比选条件将5 款手机进行对比选择，譬如C 品牌最好，D 次之; B 摄像效果最好，E 次之; D 性价比最高等。最后将每个层次的比较判断进行综合，在A ～E 手机中确定哪个作为最佳购买手机候选。

2 模型描述

层次分析法可以视为一个影响因子的分层模型。我们需要决策的结果，比如企业的绩效指标制定放置在最上层; 对于为实现这个绩效目标而细化的各个指标放置在中间层; 如果需要决策的过程目标过于复杂，比如企业内部存在分类绩效指标，则可将中间层的指标进一步细化，放置在最下层。利用层次分析法决策问题需要把各种需要考虑的因素放在适当的层次内，并用层次结构图清晰地表达这些因素的关系。

3 分析步骤

(1) 建立层次结构模型。在分析具体需要解决问题的基础上，将有关的各个因素按照不同属性自上而下地分解成若干层次。最顶层为目标层，一般只有1 个因素，最底层通常为方案层，中间可以有多个或一个层次，通常为指标层。当指标超过9 个时，应进一步分解出子指标层。

(2) 基于调查样本建立对比矩阵。利用层次分析法定义的比较尺度，按照由上至下的原则，相互对比指标之间的重要程度(以1～9 表示) ，建立矩阵表格，将基于调查样本的统计结果填充到矩阵表格中，形成基于调查样本统计结果的对比矩阵。

(3) 计算对比矩阵的特征向量，进而计算出的最终指标权重，并通过计算一致性比率进行权重一致性的有效性检验。

4 层次分析法在企业权重管理中的应用

4.1 确定指标

根据企业的业务活动和工作流程，拟定需要确定权重的评价指标清单。如罗列需要确定权重的评价指标: 生产计划、上缴款、合同管理、科技创新、获奖、事故等。

(1) 统计评价指标重要性

将需要确定权重的评价指标，排列在比较表中，如表1，请公司内部员工就其重要性进行两两比较选择。

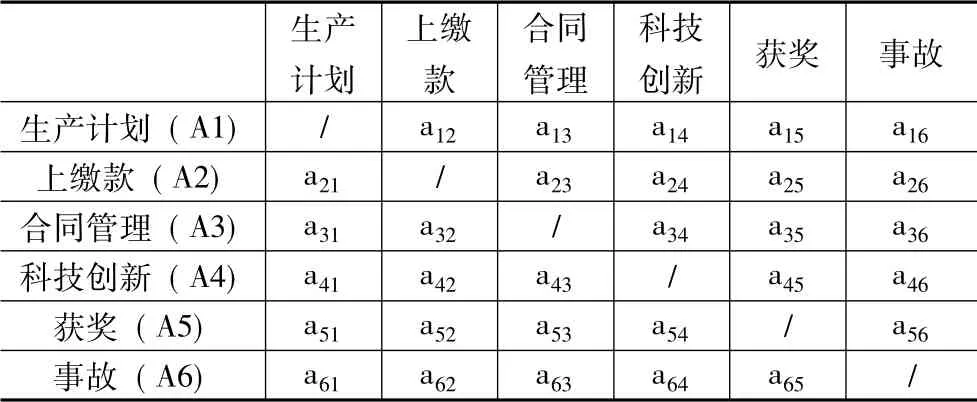
表1 评测指标比较表

例如，a21处代表2 行处的指标对比1 列处的指标的重要性，即上缴款对于生产计划的重要程度; a65处代表6 行处的指标对比5 列处的指标的重要性，即事故对于获奖的重要程度，依此类推。a21与a12、a65与a56应为倒数关系。

重要性用标度表示，如: 1 表示两个具有同样重要性(或相同强) ，3 表示一元素比另一元素稍微重要(或稍微强) ，5 表示一元素比另一元素比较重要(或比较强) ，7 表示一元素比另一元素明显重要(或明显强) ，9 表示一元素比另一元素绝对重要(或绝对强) ，2、4、6、8 则表示在上述两个标准之间折中时的标度。

(2) 构造双对比矩阵

对公司员工对于指标重要性的调查采用平均法进行汇总，计算出统计结果，形成双对比矩阵，如表2 所示。

表2 评测指标比较统计表

(3) 计算矩阵的特征向量和指标权重

对双对比矩阵，利用下面的公式1 进行归一化计算。

式中，bij就是用各列的元素除以列的和。

得到的结果为一个新的矩阵，我们暂命名为B 矩阵，

如表3。

表3 矩阵B

对矩阵B 每一行进行求和，计算出特征向量B，可知

B1=0.737，B2=1.275，B3=0.211，B4=0.350，B5=0.458，B6=2.969

上述求出的特征向量，用下面的公式2 进行归一化计算，即可得到各指标的最终权重值。

由公式可计算出各指标的权重值。

W1=0.123，W2=0.213，W3=0.035，W4=0.058，W5=0.076，W6=0.495

4.2 矩阵一致性检验

我们需要对企业绩效指标相互对比，如果存在: A＞C，C＞B，则必得出A＞B，否则就是建立的双对比矩阵存在不一致。举例来说，如果B 对于C 的重要值为2，C 对于A 的重要值也为2，那么B 对于A 的重要值应该为4，但是如果最终不是4，是5 或者9，代表对比矩阵的一致性存在一定问题。所以需要检验对比矩阵的一致性，确保两两比较的时候，不会出现以上的错误。

在检验对比矩阵的一致性时，首先需要计算对比矩阵的最大特征根，然后计算对比矩阵的一致性指标CI，再计算平均随机一致性指标RI。如果RI＞0.1，就表示计算出的指标权重未保持显著水平，对比矩阵进行调整。如果RI＜0.1，即表示计算出的指标权重保持显著水平，对比矩阵的一致性通过检验，权重计算结果有效。

5 结 论

通过层次分析法(AHP) 进行企业内部指标的权重设计，可以由众多员工进行投票评选各指标的重要性，建立对比矩阵，使得指标制定来源于科学的原始数据，间接体现了基层员工的总体意愿，避免了以往权重设计由主要决策者经验式决策的弊端，能有效提升决策权威，显著增强奖惩政策的执行力。同时，通过计算出的权重结果进行一致性检验，可以检验原始统计数量是否有矛盾，是否与对比矩阵中每组指标之间的对比标度保证一致，保证权重计算的准确性与一致性，也使得权重制定的过程更透明、更量化，符合企业的发展和激励机制的需要。

任何决策工具都不是完美的。层次分析法对于指标权重的计算主要依赖于样本统计结果，故企业在实际应用过程中，需要通过增加培训、细化调查等方式，保证调查样本的重要性与对比结果的一致性，才能保证层次分析法的准确度。