基于高中数学常见解题思想方法举隅
季宏玲
(江苏省南通市通州区金沙中学 226300)
一、基于教材的数形结合思想
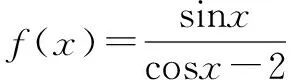
二、基于认知的化归思想应用
从大量的高中数学解题教学经验分析,化归思想有着大量的运用可能性.例如在接触到函数方面的解题要求时,两个相异变量间存在的关联性,便充分展现出了运动还有变化的思维观念,利用探索与之相对应的数量问题还有附加的依存关系,便能够较为顺利地让数学问题向函数形式进行转化,而比较研究对函数值增减性的过程中,带入至函数数量变化,由此择取静态值并构造函数,可较简便地研究自变量同函数值之间的关系.也就是说,在处理类似问题时,使化归思想得到合理应用,让问题向函数单调性分析方面转变,是对思维的调整与积极适应.我们还需要注意到,高中各类测试中求解不等式的问题出现频率也比较高,对此依然可以将化归思想应用其中.在高考时函数方程和不等式关系的问题,综合性较强,若是仅仅借助知识叠加方式,解题路径的获取难度之高可以想见,同样可以将拆分方法利用起来,让彼此关联度较高的知识点划分开来,达到不同知识模块构建的效果,并逐一化解,以此保证解题思路的清晰化.像在探索不等式解集时,为了顺利求得实数k之取值,一般来说,要把端点值加以代入,并对等号成立条件进行探索.
三、基于综合的联想方法应用
联想方法的可操作性强,对于学生的综合能力训练也极有帮助,对此解题方法进行应用时,教师的引导功能只是作为数学教学的一种辅助性方式,若想让学生真正理解并掌握此类联想方法,并据此形成相应的思考能力,则需要学生付出大量的努力,努力的过程应当强调综合性与实践性.例如在接触到与统计学有关的内容时,在基本教学内容提示完成之后,学生便能够在一定程度上理解有关的知识内容,但是牢固程度还很不够,所以需要大量的问题练习进行巩固补充.学生在处理这些问题之际,便不能只将思维停留于本次课堂所学内容,而是要按照与统计学知识有关的理论加以联想.像题目中所提的要求是借助抽查方法对学校各个年级学生人数进行调查,学生便可以将其与学生性别比例、民族比例等问题关联起来,并选择可操作性更强的普遍调查方式,从而最优化解题方法,据此将自己的联想能力提升到一个新的层次.再比如代数类问题的处理中,同样可以把接近联想的方式利用起来,所谓接近联想即按照问题中给出的已知条件,联想与之相类似的、更易于操作的方式,这种方式在解题思路中的应用可能性很高,比如下面所列的问题:现假设P是双曲线x2-4y=4上的一点,已经知道∠F1PF2是90°,那么△F1PF2面积是____.
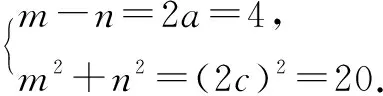
对于一名高中生来说,数学能够起到良好的思维养成与意志锻炼的作用,与此同时在考试过程中,数学也比较容易出现比分的拉大情况,为此我们可以认为,掌握一定的数学解题方法,既是图眼前的成绩“小利”,也是图未来发展的“大利”.本文简要例举了联想、化归、数形结合等方法,希望可以提供一些教法上的借鉴.

