基于入位基准线的避死区自动泊车路径规划

李茂月 陈 月 徐光岐

哈尔滨理工大学机械动力工程学院，哈尔滨，150080

0 引言

发展自动泊车技术，不仅可以减小驾驶员的泊车难度，而且对解决“一位难求”问题也有显著效果。文献[1]设计了一种泊车辅助器，可帮助驾驶员方便安全地泊车；文献[2]结合基于几何学改进的最小半径法和不等半径路径规划方法使泊车过程得到了优化；文献[3]采用多段圆弧曲线设计泊车路径，并采用回旋曲线连接曲率不连续的多段圆弧；文献[4]进行了基于轨迹跟踪控制器的泊车控制研究；文献[5]采用B样条曲线对泊车路径曲率进行平滑处理；文献[6]通过B样条曲线建立了平行车位的泊车避障约束函数；文献[7]提出了结合定点跟踪的非时间参考的路径跟踪控制策略；文献[8]应用微分平坦理论并融合动力学约束对自动平行泊车轨迹进行了研究；文献[9]采用Bezier曲线对泊车轨迹进行拟合，但未解决泊车原地转向问题；文献[10]基于微分平坦与样条理论进行了自主泊车轨迹规划研究。

为了使驾驶员更好地观察车位状态，防止有小障碍物阻碍自动泊车的进行，本文研究了与车位齐平的位置处停车的自动泊车系统。自动泊车系统开启后，驾驶员通过调节摄像头的角度来寻找空车位，当提示车位大小合适时，按下确认键后系统将开始自动计算出汽车与车位的位姿关系，驾驶员同时选择前进水平线的位置，以避免泊车死区(泊车死区是指由于汽车与车位位置较近、角度较大等原因造成的汽车不能泊入车位的区域)，进行确认后汽车将结合位姿关系规划泊车轨迹，按下执行键后，汽车开始自动进行泊车动作。该泊车动作主要分为三部分：向前行驶至前进水平线、倒车行驶至入位基准线、倒车入位。

1 自动泊车过程轨迹规划

自动泊车系统的工作流程如图1所示。当汽车准确计算出与空车位的位姿关系后，会确定出汽车在泊车过程中必需经过的几个位置点，根据三次插值样条理论[11]控制泊车路径的轨迹形状[12]，泊车路线便被确定且具有唯一性。很明显，车位长度越小，泊车系统需要进行更多次数的纠正才能使汽车完全停入车位。如果外围车辆停放复杂，汽车需要进行纠正才能避免泊车死区的存在。因此，针对前一种情况，可以优化汽车泊车所需要的最小车位长度；针对后一种情况，需要确定出泊车死区范围，从而避开该区域，以保证汽车能够完成自动泊车动作。

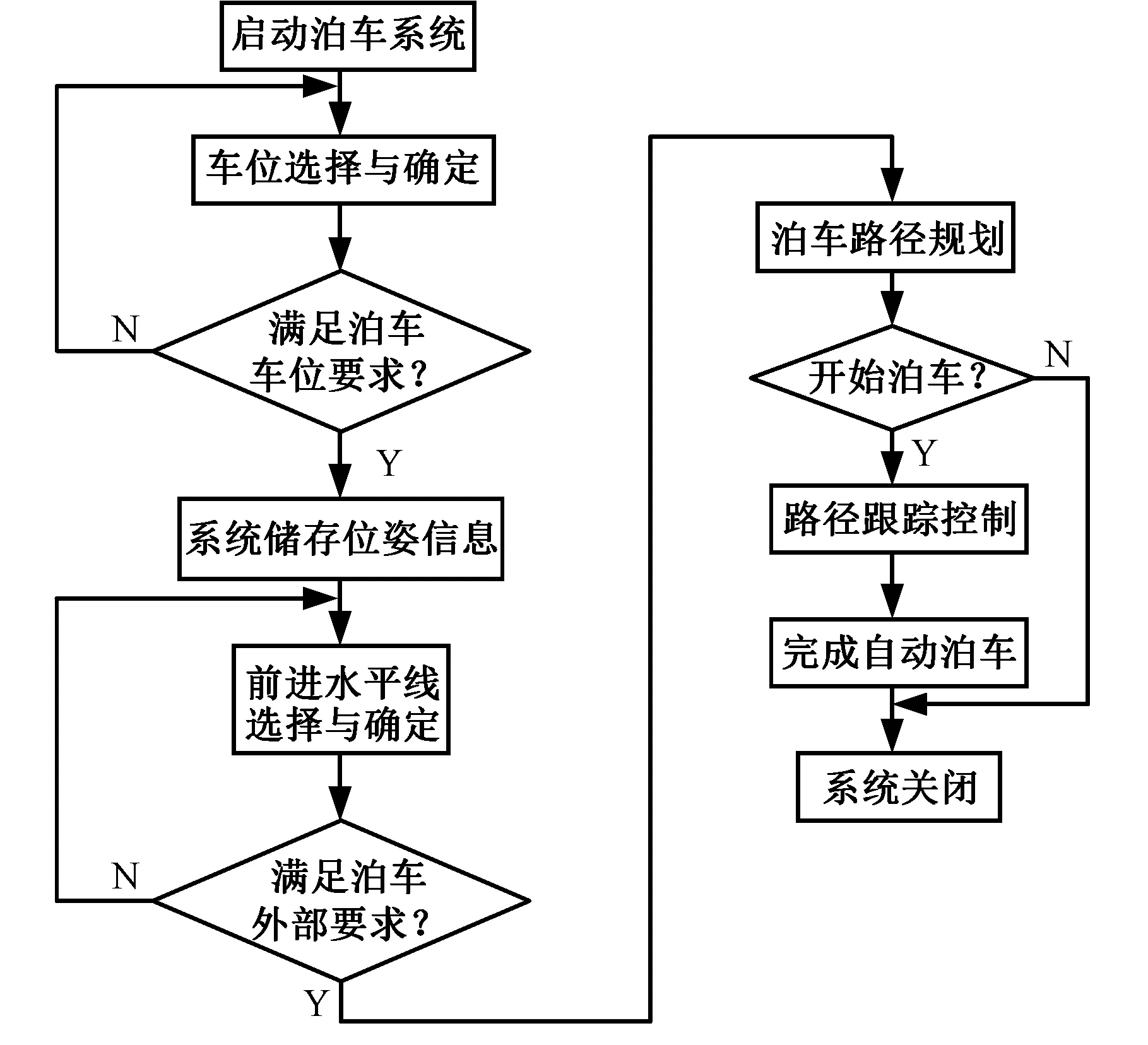
图1 自动泊车系统工作流程Fig.1 Automatic parking system workflow

本文研究的自动泊车过程包括车位外部的路径规划过程和车位内部的路径规划过程。前者的路径规划过程称为外部路径规划，包括外部前进过程和外部后退过程；后者的路径规划过程称为内部路径规划。本文主要对前者进行论述。

1.1 外部路径规划

自动泊车的第一步是向前行驶至前进水平线，然后由前进水平线倒车入位，由于前进水平线位于非泊车死区内，因此可以保证汽车一定能够泊入车位。将本文所需要的一些车位线和轨迹线进行命名，如图2所示。

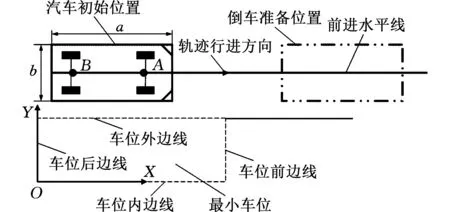
图2 自动泊车系统与车位命名示意图Fig.2 Schematic diagram naming of the automatic parking system and parking spaces

图2中，汽车初始位置为汽车探测空车位时所停止的位置；倒车准备位置为汽车行驶至最前端的位置，并由此位置开始倒车入位；前车轴中心点记为点A，表示汽车前端；后车轴中心点记为点B，表示汽车后端；以空车位的左下角为坐标系原点建立直角坐标系OXY。当汽车泊车系统探测空车位时，可以得到的已知数据有A点坐标(XA0，YA0)、B点坐标(XB0，YB0)、姿态角α，前进水平线为汽车检测空车位后自动判断的一条轨迹线，可以根据实际前方路况进行手动调节，故其与X轴的距离也为已知值。

1.2 前进水平线的选取

前进水平线与车位外边线平行且具有一定间距，该间距可以通过手动选取来进行调节。前进水平线的作用是为了避开某些阻挡在泊车线路上的障碍物。前进水平线的调节范围为：距车位外边线最小距离的前进水平线与入位基准线相交后形成的右上侧区域，因此当手动调节轨迹框向右向后调节至最小值时，继续调节将不能使轨迹框向右向后移动。

在汽车与车位的位姿关系确定结束后，中央显示屏内将显示前摄像头所采集的图像信息，且会在图像内出现汽车的前进轨迹。如图3所示，实线表示汽车的轮廓路径，虚线即为前进水平线，且由于位姿关系已确定，该三条线与车位外边线处于平行状态。通过手动选取前进水平线的位置及前端停止位置，可以改变汽车自动向前行驶的路径。

图3中前进路径没有被阻挡，表示汽车停止位置良好，不需要再进行前进水平线的调整。图4表示待泊汽车的停止位置太过靠右，汽车的前进路径轨迹被右侧车辆阻挡，导致不能向前自动行驶，因此需要进行前进水平线的调整。对于图4所示的情况，第一步需要将前进水平线向左移动，即外移至图5所示位置，该位置的前进路径右侧将不会被右侧的车辆阻挡，但左侧将会被车辆1阻挡，因此还需要将前进路径的前端向后移动至图6所示位置(当前位置与后移位置间有最小阈值)，此时汽车的整个行车路径都不会被阻挡，可以完成自动向前行驶和避死区的动作过程。

图4 前进路径右侧被阻挡Fig.4 The right side of the path is blocked

图5 左移后前进路径前端被阻挡Fig.5 The front end of the forward path is blockedafter moving left

图6 下移后前进路径没有被阻挡Fig.6 The path is not blocked after moving down

1.3 外部前进过程纠正方法与轨迹计算

根据阿克曼转向几何原理[13]，可以确定出汽车的转弯圆心。当左/右打满汽车转向盘时，汽车上任何一点均绕该几何圆心运行，对汽车的前后车轴的中心点绕圆心的轨迹半径进行标定，对汽车与车位的其他名称与符号进行汇总，如表1所示。

表1 汽车及车位的参数与符号

图2所示为最简单的外部纠正，即汽车由初始位置直接向前行驶至倒车准备位置，此时不需要进行角度纠正，只需向前行驶即可。除了上述情况外，由于汽车在初始位置处，车头可能偏左，也可能偏右，本文以车头偏右为例进行分析(向左情况相似)，存在下述3种情况：

(1)情况1。汽车的前后车轴中点均位于前进线左侧，如图7所示，即均在前进水平线上侧，则计算汽车所需要的转弯半径，控制转向盘的左转角度，行驶至前进水平线。

该情况下，汽车需经过起始点A1和前进水平线起点A2，汽车与前进水平线夹角为α，即以O1点为圆心进行转向需要扫过的角度为α，前车轴中心点将由A1沿圆弧A1A2运动至A2，其中A1和A2的纵坐标分别为YA1、Y0，其值均已知，则可以根据下式计算出此时所需要的转弯半径：

(1)

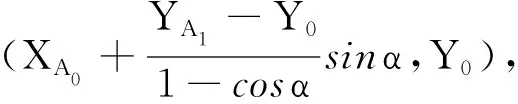
点A1至点A2运动过程中，ω为绕O1扫过的角度，其值是变化的，轨迹方程为

(2)

其中，XA0=XA1，YA0=YA1，ω变化范围为270°-α～270°。

(2)情况2。汽车的前车轴中点位于前进水平线右侧，后车轴中点位于前进水平线左侧，如图8所示。此时需要先计算汽车左打满转向盘的情况下，沿圆弧A1A2行驶至与前进水平线平行状态(其扫过的角度大小为α)，并计算出此时所在平行线与前进水平线的距离差LX，通过“先左打满再右打满”的方法，即汽车先继续保持转向盘左打满状态沿圆弧A2A3行驶，当行驶至点A3时，将转向盘改为右打满状态，沿圆弧A3A4行驶，并继续向前行驶一小段距离X3使前车轴中心点A、后车轴中心点B同时处于前进水平线上。

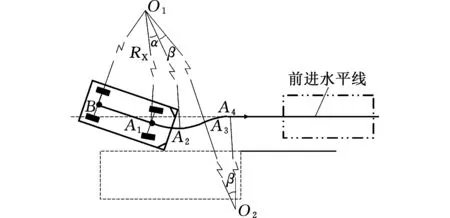
图8 情况2示意图Fig.8 Schematic for the case 2

(3)情况3。汽车的前后车轴中点均位于前进水平线右侧，如图9所示，即均在前进水平线下侧，也需要经过先行驶至水平状态再进行“先左打满再右打满”的转向模式，计算方法与情况2类似。

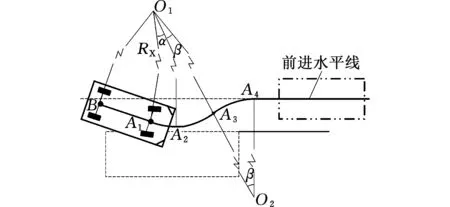
图9 情况3所述示意图Fig.9 Schematic for the case 3

由于情况2和情况3的计算方法相同，因此可将轨迹线绘制于图10进行计算。

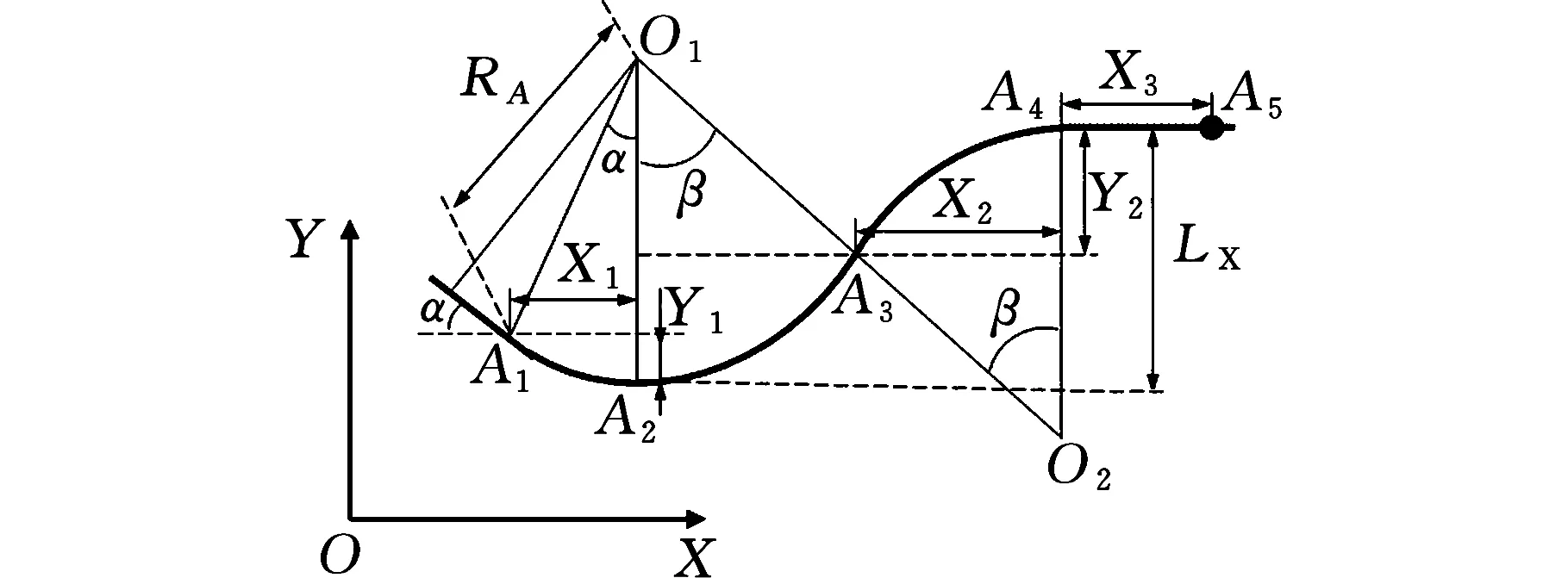
图10 轨迹计算标识图Fig.10 Trajectory calculation identification diagram

这两种情况(情况2和情况3)分为三阶段：第一阶段点A1至点A2，第二阶段点A2至点A3，第三阶段点A3至点A4。其中，第一阶段点A1至点A2的计算方式与情况1相同，见式(1)，第二、第三两个阶段关于点A3对称，因此仅需计算第三阶段，即能得出第二阶段的数据。

根据图10的几何关系得

(3)

其计算结果为

(4)

在上述泊车过程中，汽车经过的点为起始点A1，第一次水平切点A2，过渡中间点A3和第二次水平切点A4(即前进水平线起点)。

点A2的坐标为

点A3的坐标为

点A4的坐标为

点A5的坐标为

Y0+LX)

由上述各个点的坐标，确定各阶段轨迹方程如下。

点A2至点A3运动过程中，ω为绕O1扫过的角度与α的差值，记为β，其值是变化的，轨迹方程为

(5)

其中，ω变化范围为270°～270°+β。

点A3至点A4运动过程中，ω为绕O2扫过的角度，其值是变化的，轨迹方程为

(6)

其中，ω变化范围为90°+β～90°。

点A4至点A5运动过程中，XX为汽车前进的距离，轨迹方程为

(7)

其中，XX的变化范围为(0，X3)。

1.4 外部后退过程纠正方法与轨迹计算

汽车由前进水平线倒车至入位基准线的轨迹分析如图11所示，当汽车的前后车轴中心点均位于图中阴影部分时，汽车便一定可以泊入车位。当设定的前进水平线与车位外边线的距离大于Ymin时，则汽车不会存在泊车死区。

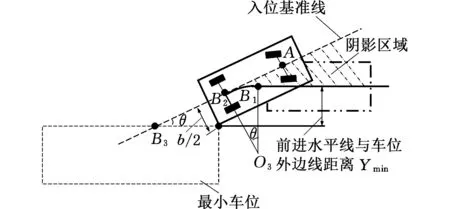
图11 前进水平线与车位外边线距离示意图Fig.11 Schematic diagram of the distance between theforward horizontal line and the outside line ofparking spaces

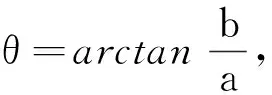
(8)

故自动泊车时需保证前进水平线与车位外边线距离满足Y0≥Ymin。

汽车由前进水平线至完全泊入车位时的轨迹如图12所示，当汽车行驶至所设定的前进水平线后，汽车开始进行倒车动作，此后以车轴中心点B为轨迹点，将依次经过点B1、B2、B3、B4、B0，当倒车至点B1时汽车转向盘右打满，转弯半径为RB，沿圆弧B1B2倒车，进入入位基准线。该过程中，汽车必经过起始点B1和入位基准线起点B2。由于已知点A1的坐标和轴距，故点B1的坐标也已知，记为(XB1,YB1)，则点B2的坐标为(XB1-RBsinθ，YB1-RB(1-cosθ))。

图12 一次泊车入位示意图Fig.12 The diagram of one-time automatic parkinginto the parking space

从点B1运动至点B2的过程中，绕O3扫过的角度ω是变化的，点的轨迹方程为

(9)

其中，ω变化范围为90°～90°+α。

如果车位长度足够，当汽车进入入位基准线后倒车至点B3时，汽车与车位的位置状态为汽车的右前角点与汽车的左后角点同时位于车位外边线上，并且汽车的右前角点与车位外边线及车位前边线的交点重合，此时汽车保持转向盘左打满状态，沿圆弧B3B4行驶至点B4，并后退一段距离至B0，以保证汽车整个车身完全进入车位内并与车位保持平行，结束泊车动作。

该过程中，汽车必经过起始点B1、入位基准线起点B2、入位基准线终点B3、第一折点B4。

其中，B3坐标为

B4坐标为

B0坐标为

由上述各个点的坐标，确定各阶段轨迹方程如下。

点B2运动至点B3过程中，轨迹方程为

(10)

其中，x的变化范围为点B2至点B3的横坐标变化范围。

点B3至点B4运动过程中，ω为绕O4扫过的角度，其值是变化的，轨迹方程为

(11)

其中，ω的变化范围为270°+θ～270°。

点B4至点B0运动的过程中，轨迹方程为

(12)

其中，x′的变化范围为(0，X4)。

由于汽车的前车轴中心点A与后车轴中心点B的轴距差为LZ，且其值已知，因此可以将点A和点B的运动方程全部表示出，汽车运动方式即可确定。

2 倾斜与垂直车位的轨迹规划

倾斜车位属于垂直车位的延伸模式，如图13所示，虚线为垂直车位，实线为倾斜车位，倾斜车位时汽车与车位的各种位置情况都与垂直车位类似，这两种车位的轨迹规划类似于平行车位。

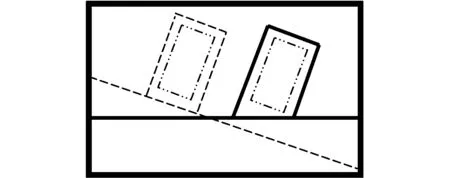
图13 倾斜车位与垂直车位Fig.13 Tilted and vertical parking space

对于垂直车位，第一步仍然是为避开泊车死区而向前行驶至前进水平线，然后开始倒车至车位内，如图14所示。

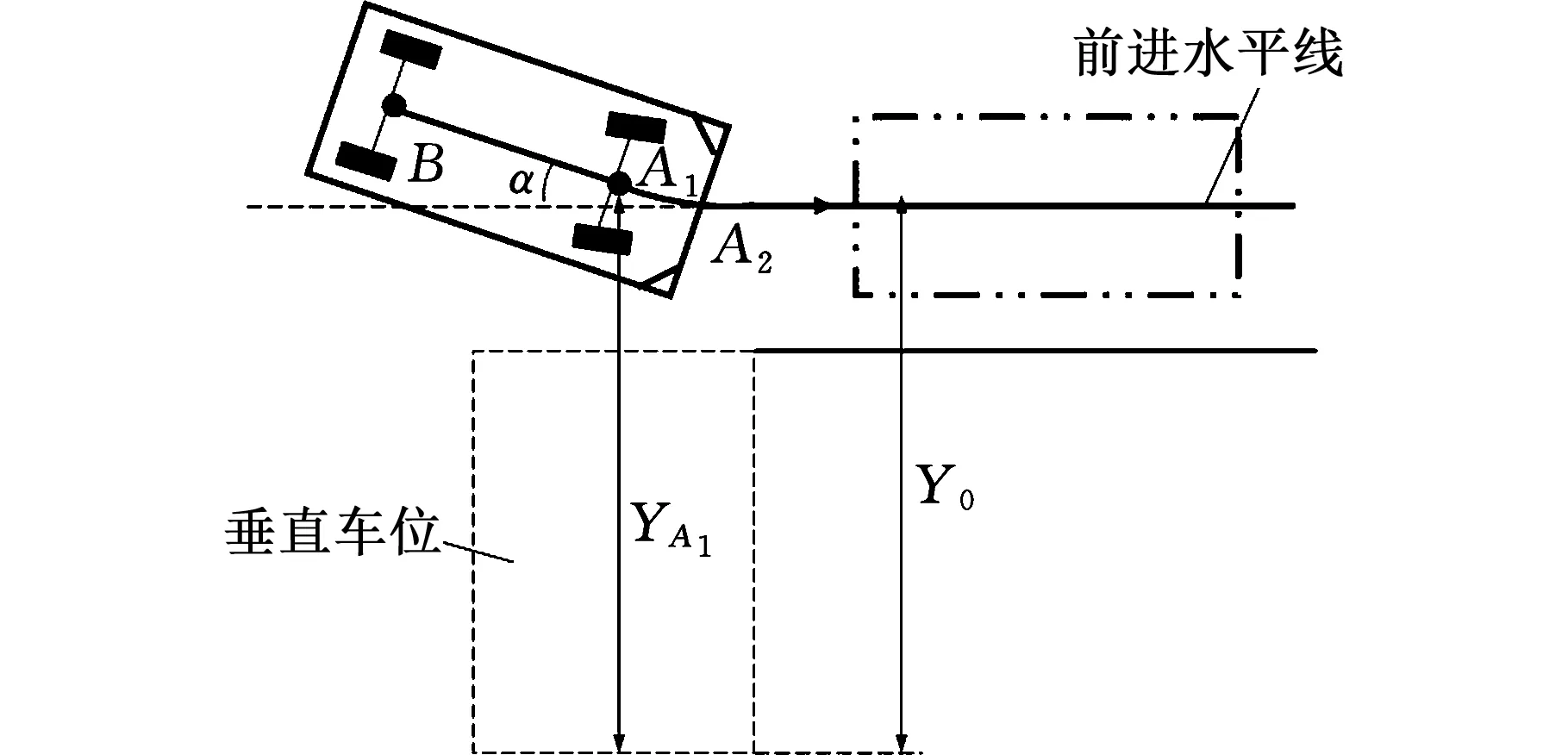
图14 垂直车位的避死区路径规划Fig.14 Path planning to avoid the dead zone forvertical parking

垂直车位时的泊车轨迹如图15所示，此时需要保证汽车转过的角度θ为90°，并根据不同的前进水平线决定不同的后退距离。由于不同的前进水平线会对应不同的车位大小，因此该轨迹规划方法并不能确定出最小车位的大小。但由于垂直车位需要对乘客的上下车提供足够的预留空间，因此车位的宽度一般都能达到需求。

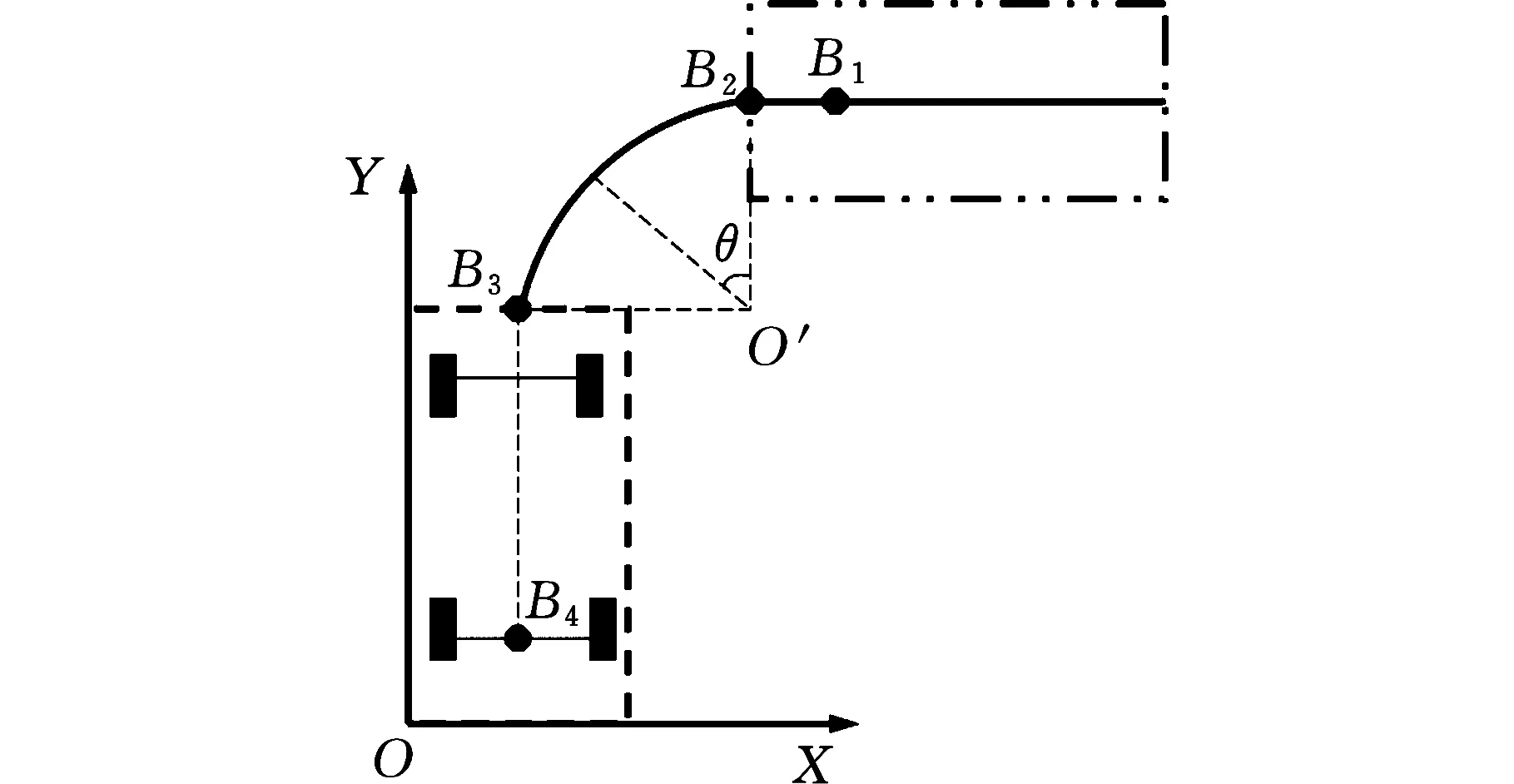
图15 垂直车位路径轨迹计算图Fig.15 Vertical parking path trajectorycalculation diagram

为了求出垂直车位的泊车轨迹方程，建立图15所示的坐标系，汽车的后车轴中心点将依次经过点B1、B2、B3、B4，完成泊车动作。

从点B1运动至点B2过程中，轨迹方程为

(13)

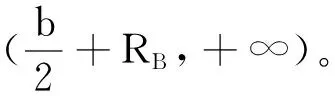
从点B2运动至点B3过程中，θ为绕O′扫过的角度，其值是变化的，轨迹方程为

(14)

其中，ω的变化范围为(0，90°)。

从点B3运动至点B4过程中，轨迹方程为

(15)

其中，n的变化范围为(LZB,a)。

但由于前进水平线的选取距离不同，所需的车位大小也不相同，因此有图16所示的车位与不同前进水平线的关系，其车位的宽度W和高度H如下：

(16)

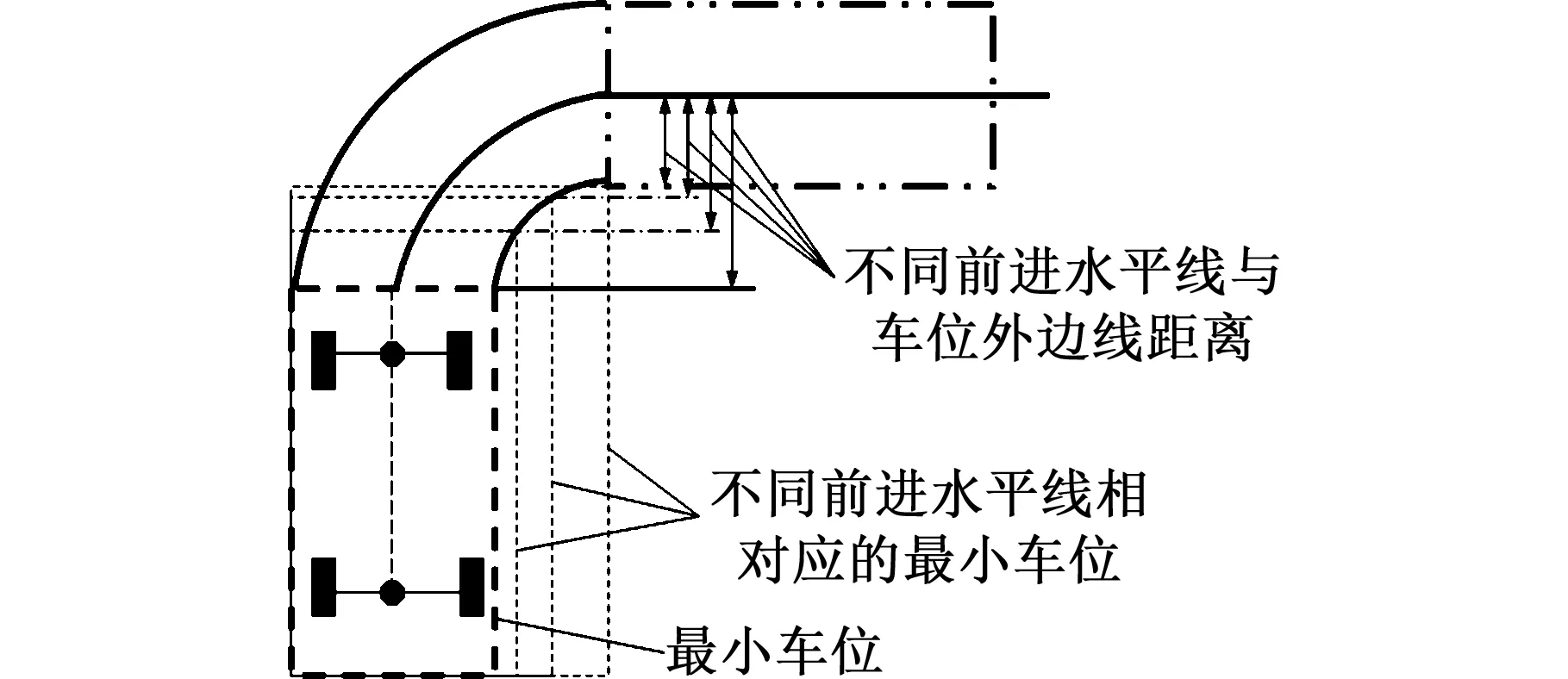
图16 不同前进水平线对应不同的垂直车位Fig.16 Different forward horizontal lines correspondto different vertical parking spaces

如图17所示，对于倾斜车位，由于倾斜角度不同，因此倒车路径的终止时间点不同，从而泊车过程更易适应。另外，车辆停入倾斜车位时相邻两车的车门并不是相对的，因此能够减小相邻车位的间距，并在相同的空间内规划出更多的车位。

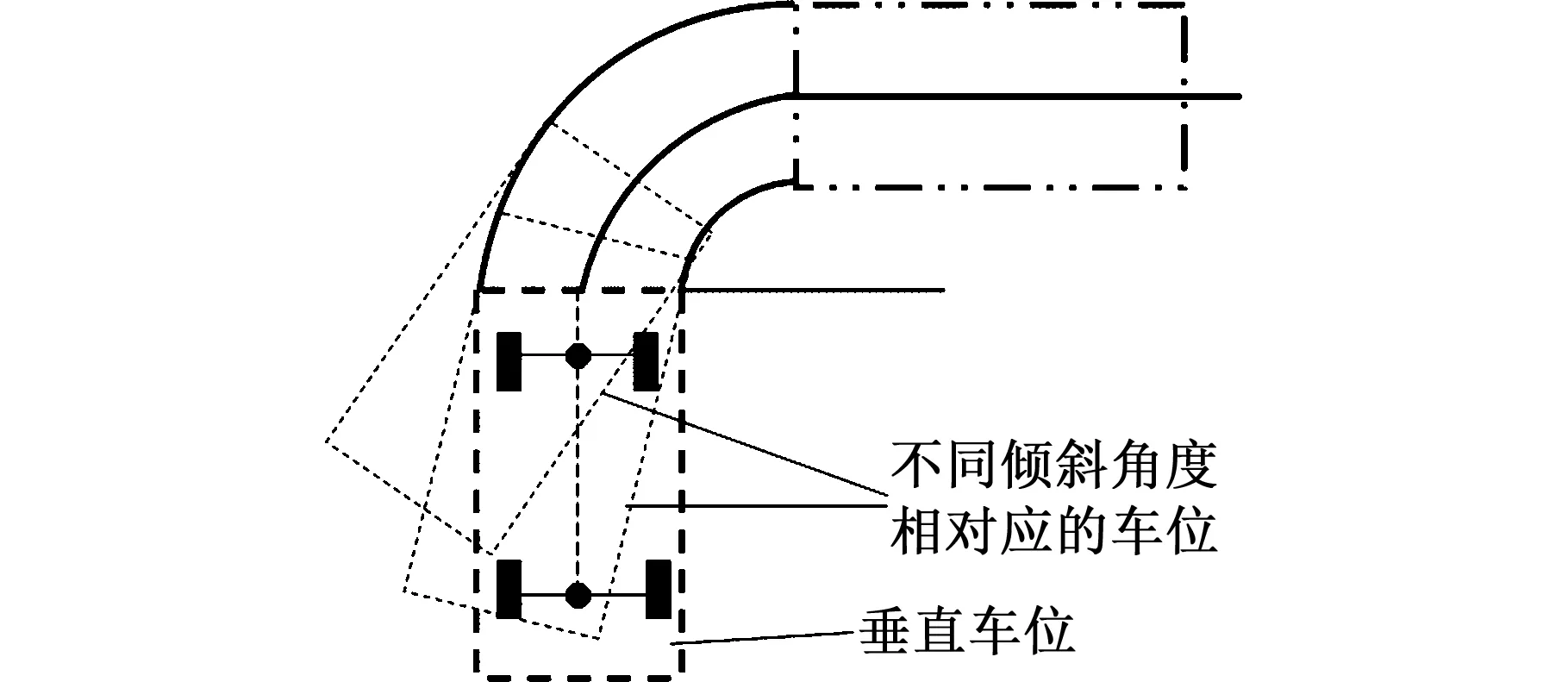
图17 倾斜车位(没有停泊完全的垂直车位)Fig.17 Tilting parking spaces(not parking completelyvertical parking spaces)

3 仿真实例及实验验证

3.1 仿真实例及分析

由上述方法建立泊车轨迹模型，对车辆的运行轨迹使用CarSim软件进行仿真，并将轨迹点导出后通过MATLAB软件进行绘制和结果分析。其中车辆参数见表2，仿真的结果见图18、图19。

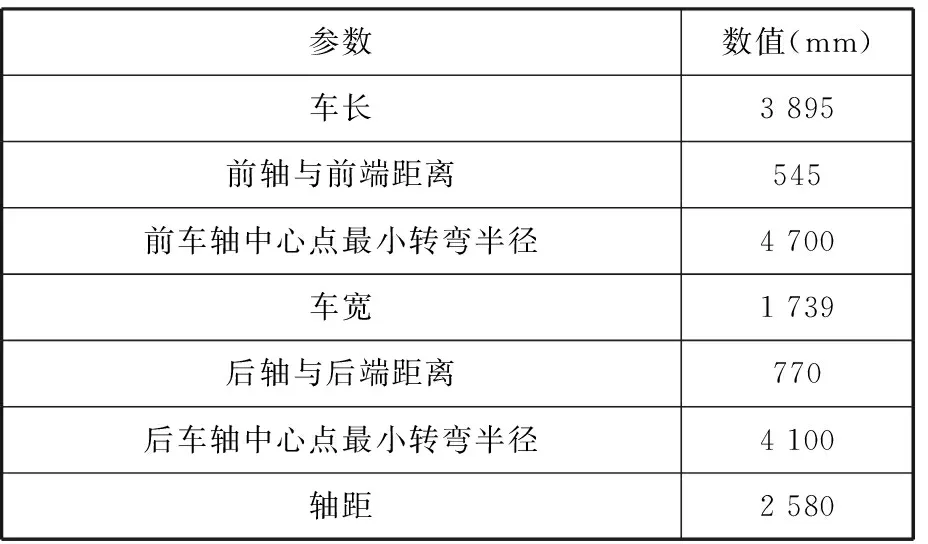
表2 车辆参数

(a)起点(0，3.997 6 m)至前进水平线5.25

(b)起点(0，4.650 0 m)至前进水平线5.25

(c)起点(0，3.997 6 m)至前进水平线6.00

(d)起点(0，4.650 0 m)至前进水平线6.00图18 不同起点前进修正至不同前进水平线的前轴中点运动仿真图Fig.18 The front axle center points motion simulation diagram from different starting points to different forward horizontal line

将车辆参数代入式(8)中，可得Ymin=1 464.07 mm，即车身纵向中心线离车位上边线的最小距离应不小于上述值，且进行仿真时需保证前进水平线与车位外边线距离大于此值。分别选取前进水平线的纵坐标为5.25 m和6.00 m(下文简称为前进水平线5.25和前进水平线6.00)进行分析。

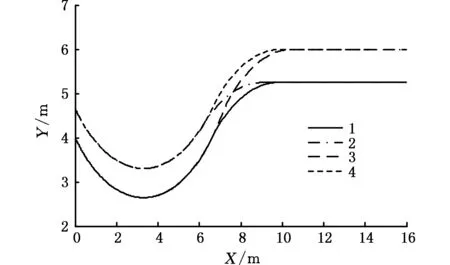
图19 不同起点前进修正至不同前进水平线的前轴中点运动轨迹Fig.19 The front axle center points trajectory from different starting points to different forward horizontal line

为证明该方法的适用性，选取三种泊车因素，保持其中两项因素相同，改变另一项因素进行验证。这三种泊车因素分别为：起始点位置与角度、前进水平线的选取位置、车位长度。将汽车的起止点选取为起点A(0，3.997 6 m)和起点B(0，4.650 0 m)。

对于前进水平线5.25，从起点A和起点B出发，分别进行运动过程仿真，如图18a和图18b所示，前车轴中心点的外部前进纠正轨迹分别见图19中的曲线1和曲线2。对于前进水平线6.00，从起点A和起点B出发，分别进行运动过程仿真，如图18c和图18d所示，前车轴中心点的外部前进纠正轨迹分别见图19中的曲线3和曲线4。

图19中，曲线1表示起点(0，3.997 6 m)到达前进水平线5.25时的前车轴中点运动轨迹，曲线2表示起点(0，4.650 0 m)到达前进水平线5.25时的前车轴中点运动轨迹，曲线3表示起点(0，3.997 6 m)到达前进水平线6.00时的前车轴中点运动轨迹，曲线4表示起点(0，4.650 0 m)到达前进水平线6.00时的前车轴中点运动轨迹。

对上面两个起点和两条前进水平线的路径利用CarSim软件进行仿真后，将所得的数据点导入MATLAB软件进行曲线绘制以及运动分析，结果表明：汽车在寻找空车位时所停位置与车位的位姿关系不会影响汽车的外部前进动作，汽车将自动行驶至前进水平线，且当前进水平线的纵坐标距离大于最小距离Ymin时，汽车将避过泊车死区，且一定能够完成泊车入位动作。

对比本文所述的泊车死区问题，目前的自动泊车系统也有少量涉及，文献[14]中的泊车可行区域如图20所示，通过MATLAB仿真，当汽车后车轴中心点位于深色区域，汽车能够倒车泊入车位，但该种泊车模式并不具备本文介绍的向前行驶修正到非泊车死区的功能，因此不具有主动避开泊车死区的能力。

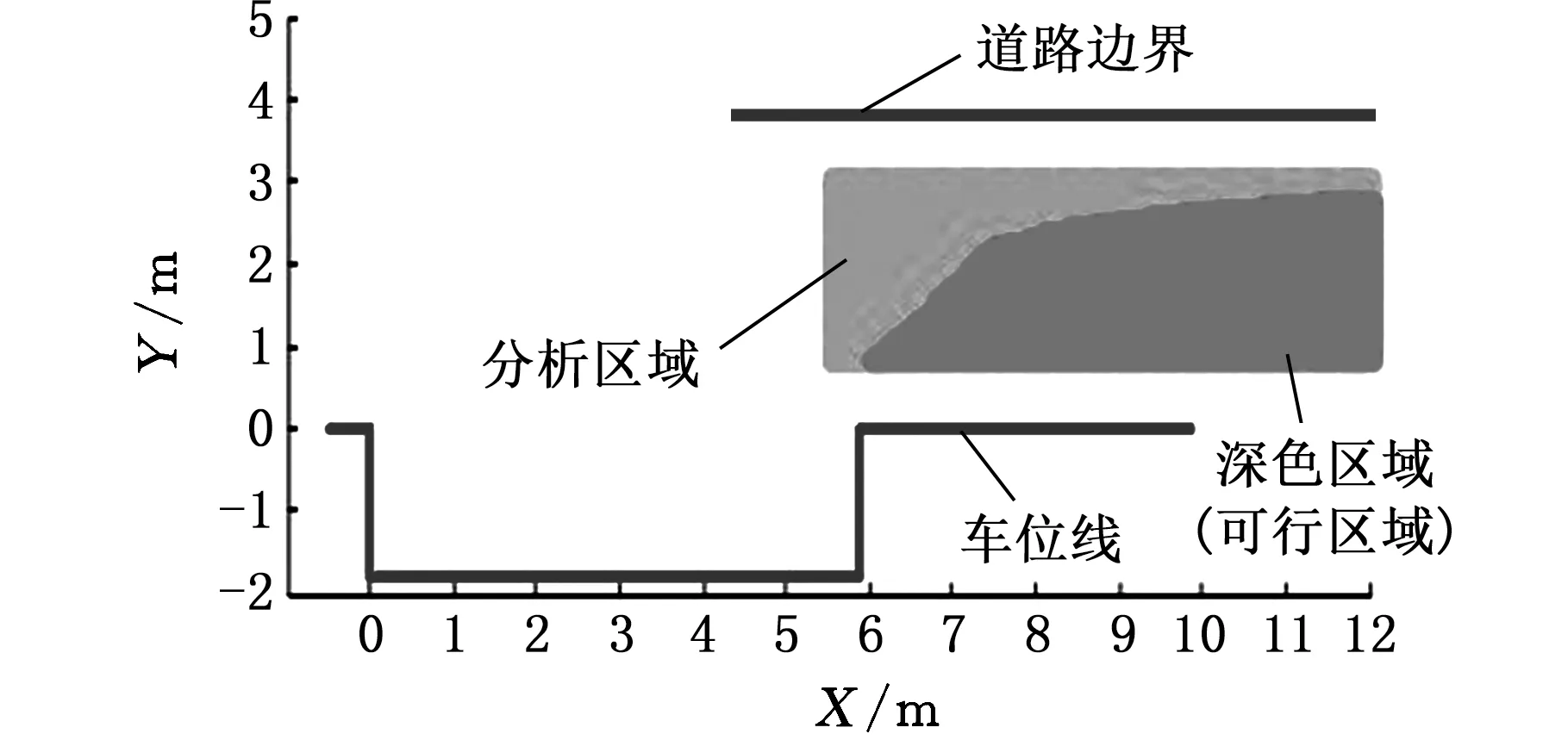
图20 自动泊车倒车可行区域(非泊车死区区域)[14]Fig.20 Automatic parking reversing feasible area (non-parking dead zone)[14]

对于前进水平线5.25和6.00，当汽车分别以这两条线为起点开始倒车至车位内，其运动过程仿真分别如图21a和图21b所示，后车轴中点的运动轨迹和前车轴中点的运动轨迹分别如图22中的曲线5～曲线8所示。

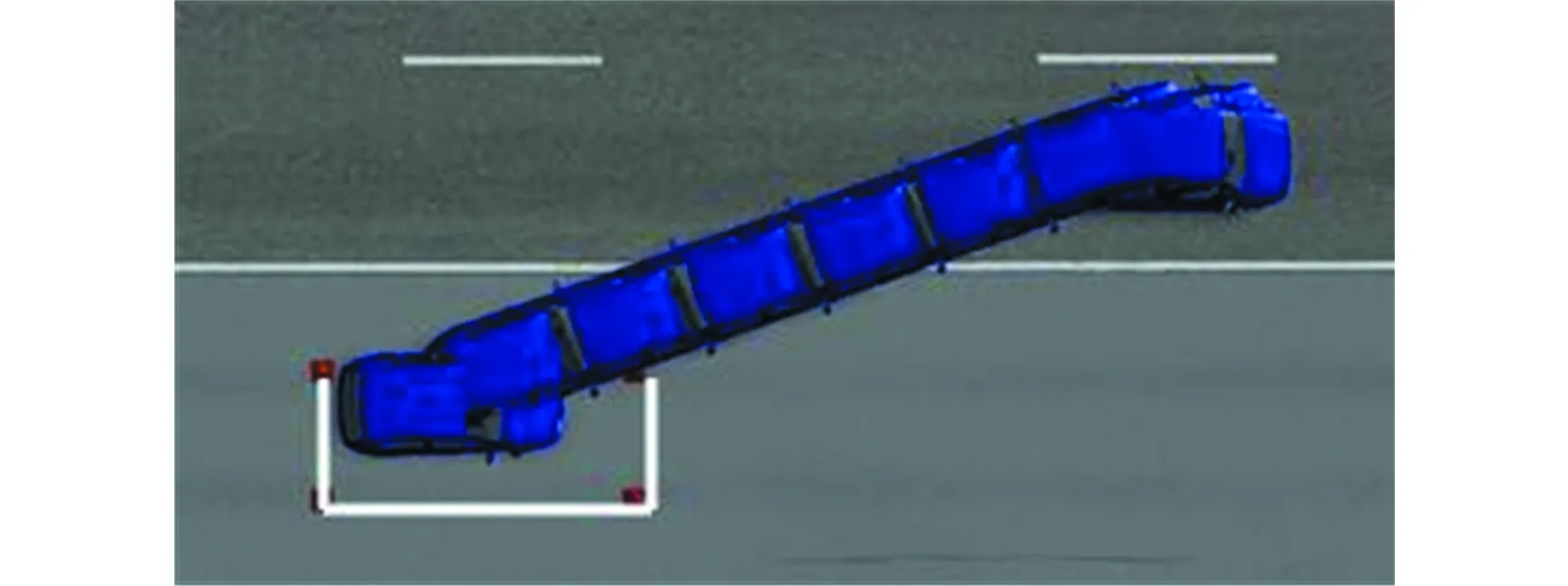
(a)前进水平线5.25倒车至车位

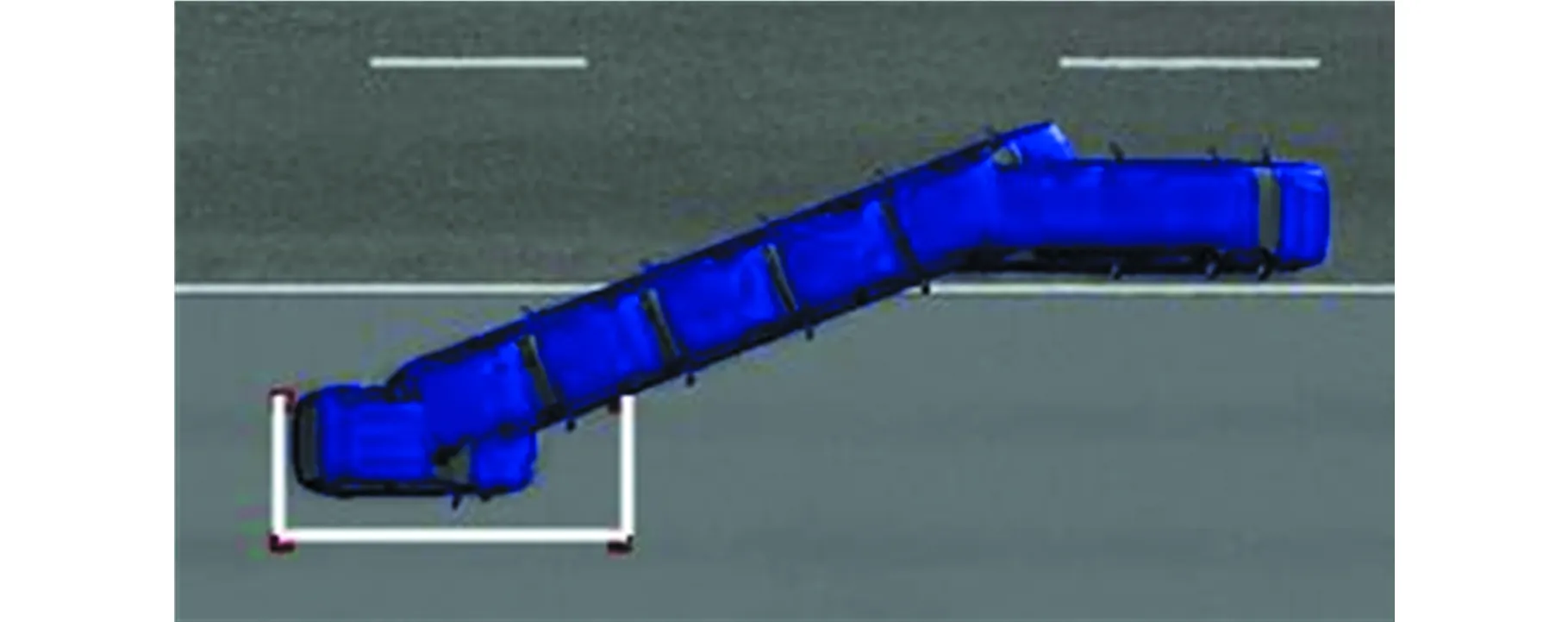
(b)前进水平线6.00倒车至车位图21 前进水平线5.25和6.00倒车至车位运动仿真图Fig.21 Simulation diagrams of forward horizontal line 5.25 and 6.00 reversing to the parking movement

图22中，曲线5表示从前进水平线5.25起点倒车至车位时后车轴中点的运动轨迹，曲线6表示从前进水平线5.25起点倒车至车位时前车轴中点的运动轨迹，曲线7表示从前进水平线6.00起点倒车至车位时后车轴中点的运动轨迹，曲线8表示从前进水平线6.00起点倒车至车位时前车轴中点的运动轨迹。

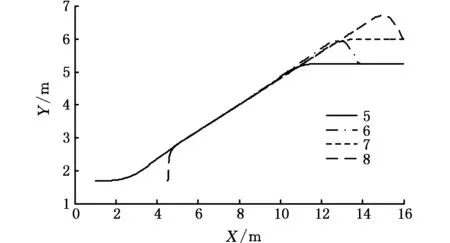
图22 不同前进水平线倒车至车位时前后车轴中心点的运动轨迹Fig.22 The trajectories of the center points of the front and rear axles with different forward horizontal lines

对上文所述的从两条前进水平线起点倒车至车位内的过程进行分析，结果表明：汽车外部倒退过程的轨迹与前进水平线的位置有关，两者形状相同，但切入入位基准线的位置点不同；入位基准线仅有一条，且与汽车的外形参数有关，汽车在进入入位基准线后，进行内部倒退过程动作时，将有且仅有一条泊车轨迹，该泊车轨迹与车位长度有关。

针对单步平行泊车所需要的最短车位长度，文献[13]基于B样条理论的主动泊车方法，给出了最小车位长度的计算公式如下：

M=

(17)

将汽车参数值代入式(17)，得出所需车位最小长度为5.67 m，而按照本文规划方法用CarSim仿真时的车位长度为5.00 m，可见本文所述的自动泊车轨迹规划方法可以减小所需最小车位长度的11.82%。

3.2 实验验证

搭建了基于stm32的智能实验车，如图23所示，通过WiFi与PC端相连，PC端用于分析采集的车位信息，将处理的结果传送回stm32开发板，由stm32开发板控制实验车的运动。

图23 模拟实验车Fig.23 Simulation of experimental vehicles

3.2.1平行车位实验验证

通过坐标纸可以快速地将实验车放在所期望的初始位置，例如将实验车的初始位置放置在纵坐标为100 mm处，如图24所示。模型实验车参数如表3所示。

图24 实验车初始位置的纵坐标为100 mmFig.24 The ordinate of the experimental vehicle initial position is 100 mm

表3 模型实验车参数mm

实验中，将车速设定为120 cm/min，每次停止时均对电动机加入锁止信号以防止实验车因惯性而移动。以坐标纸的左下角定位原点，通过计算，得到实验车所要经过的必须点，并控制电机驱动时长，来验证实验车能否泊入车位。其中，车位的上边线的起止坐标点分别为(100 mm，0)和(500 mm，0)。实验车前车轴中心点的初始位置为(300 mm，100 mm)，前进水平线选取为150 mm。将前车轴中心点的经过位置点、电机开启时长分别标入表4，实验车将自动向左前行驶至选取的前进水平线，如图25所示。

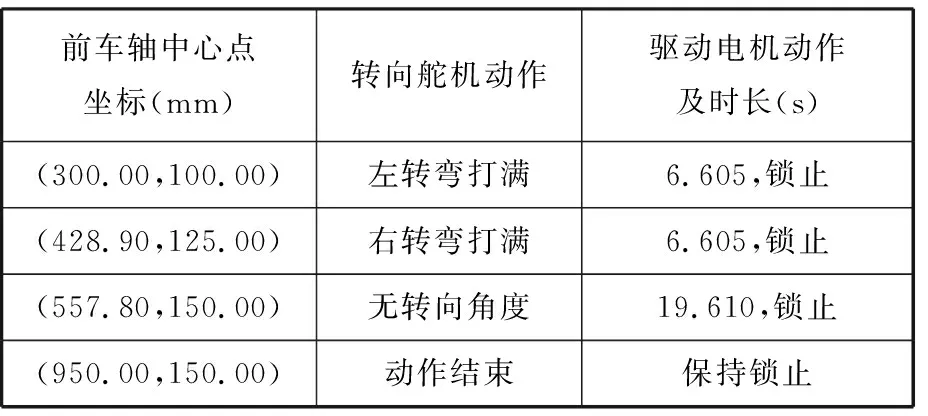
表4 实验车前进控制

图25 实验车向左前行驶至纵坐标为150 mm的前进水平线Fig.25 The experimental vehicle drives to the forward horizontal line towards the left with anordinate of 150 mm

当实验车向前行驶到达选取的前进水平线后，开始执行向后倒车泊入车位动作，此时以实验车的后车轴中心点为位置点，由于轴距为198 mm，即起点由(950 mm，150 mm)变为(752 mm，150 mm)，将后车轴中心点的经过位置点、电机开启时长分别列入表5，倒车至入位基准线的位置如图26所示，倒车直至完全泊入车位如图27所示。

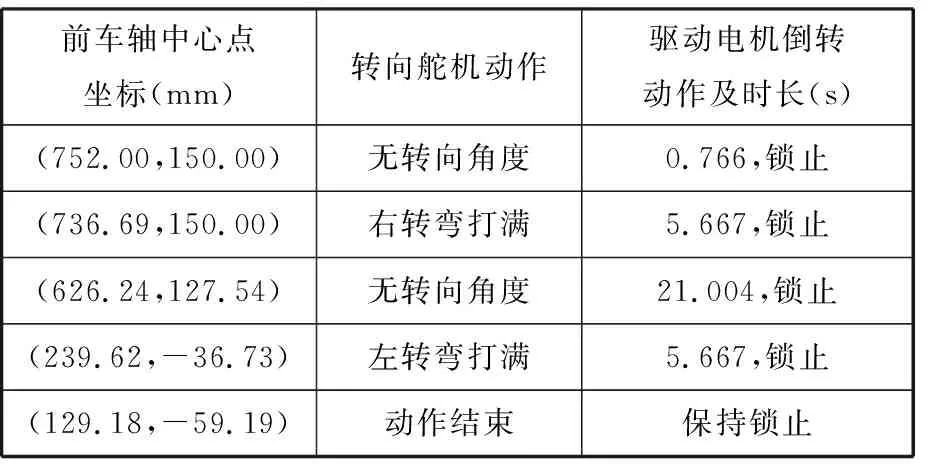
表5 实验车倒车控制

图26 实验车倒车至入位基准线Fig.26 The experimental vehicle is reversing to the entry baseline

图27 实验车完全进入车位Fig.27 The experimental vehicle is completely in the parking space

3.2.2垂直车位实验验证

对于平行车位的向前自动行驶，已证明其可行性，因此对于垂直车位则不再进行自动前行部分的实验，直接将实验车的后车轴中心点放至在坐标纸的(660 mm，300 mm)处，车位外边线的起止坐标点为(180 mm，0)和(420 mm，0)，按表6依次进行控制，将实验车泊入空车位内。对于垂直车位的实验如图28所示。

通过控制实验车的运行轨迹，可以保证实验车泊入车位内，因此可以证明提出方法的可行性。

表6 实验车倒车控制

(a)实验车向后倒车运动 (b)右打满向后运动

(c)打正方向向后倒车 (d)倒车至完全进入车位后停止图28 模拟垂直车位自动泊车Fig.28 Analog vertical parking automatic parking

4 结论

(1)设计了一种汽车自动泊车系统的外部路径规划方法，使汽车通过前进行驶动作修正汽车与车位的位姿关系，从而避免泊车死区。

(2)规划了一条以入位基准线为基础的泊车线路，避免了自动泊车系统在泊车过程中不断反馈信息进行路径修正的方式，减少系统计算量。

(3)通过将垂直、倾斜车位与平行车位的路径规划进行类比，验证了该自动泊车方式能够适应不同的车位类型。

(4)仿真结果表明，优化泊车路径在平行车位的应用中可以使所需车位长度减小11.82%。