稻谷外壳拉伸力学性能实验研究

李 阳 李永祥 曹宪周 王明旭 崔 帆

(河南工业大学，郑州 450001)

我国是稻谷生产和消费大国，国内有60%以上的人口以大米为主要食物[1]。根据国家统计局数据，2017/18年度我国的稻谷总产量预计为20 856万t，国内稻谷总消费量预计为18 560万t[2]。稻谷在收获、流通、加工过程中由于外力和自身属性等原因，会产生裂纹、破碎，对后续加工、储存等影响较大[3-4]。数据显示，稻谷在收获、流通、加工过程中的平均损失率达20%[5]，造成了严重的浪费及企业经济效益的下降。稻谷外壳对内部的米粒有保护作用，它的力学特性与收割、储藏、加工的米粒破碎相关，因此稻谷外壳力学特性的研究对粮食安全生产及提高企业经济的效益十分重要。

目前，国内外主要对稻谷和稻谷籽粒(糙米)的力学特性进行了研究，如李耀明等[6]对稻谷和糙米的挤压力学性能进行了研究，得出稻谷外壳对降低稻谷在收获、流通、加工过程中所产生的损伤有影响；Siebenmorgen等[7-8]研究了糙米的压缩强度、三点弯曲强度与整精米率的相关性关系,得出糙米三点弯曲力与整精米率相关性较大；任祖方等[9]进行稻谷的挤压和剪切试验,得出稻谷品种和含水率对稻谷力学性能的影响；丁林峰等[10]进行稻谷压缩试验，得出稻谷的弹性模量和泊松比等常用力学参数；周显青等[11]进行糙米的锥刺、三点弯曲、剪切、挤压试验，得出糙米断裂主要与厚度及胚乳特性有关。但对于稻谷外壳的力学特性，目前并未引起大多数学者的重视。

本研究运用TMS-Pro物性分析仪进行稻谷外壳拉伸实验，得到稻谷外壳的拉伸力学参数、力-位移曲线；运用电子显微镜对稻谷外壳拉伸断裂裂纹处进行显微观察，并结合力-位移曲线分析拉伸断裂过程；运用MINITAB对稻谷外壳拉伸破坏前的力和位移参数进行多项式回归分析；运用MINITAB对不同产地的籼稻稻谷外壳拉伸力学参数进行差异显著性分析。

1 材料与方法

1.1 实验设备

选择TMS-Pro物性分析仪及自制拉伸实验夹具进行实验，自制拉伸实验夹具如图1所示，物性分析仪的力感应单元量程为500 N，力检测精度优于0.015%，位移指示精度0.000 1 mm，整个实验系统采用计算机控制，配套专用分析软件，利用该分析软件可记录完善的实验数据。稻谷外壳断裂处的显微观察采用ZYJ-1000E型电子显微镜(上海兆仪光电仪器厂)。对稻谷外壳的外形尺寸测量采用精度为0.02 mm的游标卡尺。实验装置如图2所示。

1.2 实验材料

实验所选用稻谷样本分别为产自江西、广西、安徽的籼稻，稻谷样本的含水率控制在14.8%。首先去掉瘪谷和病谷，选取颗粒饱满的籽粒，剥去稻谷外壳，用医用手术刀将稻谷外壳沿长轴方向加工为宽 2 mm，长6 mm的长方形试样，试样完好无破损和撕裂。

注：1.夹具上夹头,2.调节螺栓,3.弹簧,4.夹具下夹头。图1 拉伸实验夹具

注：1.机架，2.加载装置附带力感应单元，3.拉伸夹具上夹头，4.稻谷外壳试样，5.拉伸夹具下夹头6.底座，7.计算机，8.打印机。图2 拉伸实验设备

1.3 实验方法

在TMS-Pro物性分析仪上设置加载速率为5 mm/min，夹具间距为0.5 mm，拉伸距离为1 mm，初始拉力为0.75 N。对每个产地稻谷外壳试样进行20组拉伸实验，实验过程中保证试样在夹具间断裂，对同一产地的稻谷外壳拉伸实验数据取平均值,结果保留3位有效数字[12]。

2 结果与分析

2.1 稻谷外壳拉伸力-位移曲线分析

稻谷外壳拉伸力-位移曲线如图3所示。

图3 安徽稻谷外壳拉伸力-位移曲线

从图3可知，进行稻谷外壳拉伸实验时，力与位移的曲线为非线性，曲线可以分为OA、AB、BC三段段,OA段为稻谷外壳从受到拉力至断裂的过程，随着拉伸力的逐渐增大曲线呈逐渐上升趋势,曲线峰值处A点即为稻谷外壳断裂点，A点对应纵轴的值即为稻谷外壳拉伸破坏力；从AB段可以看出此段曲线总体呈下降趋势,但该区间仍存在几个波峰,这是由于在进行稻谷外壳拉伸实验过程中当曲线到达A点处稻谷外壳总体断裂,但是还存在一些韧性较大的稻谷外壳纤维没有立即断裂,随着实验的进行这些纤维逐渐断裂,这些断裂即表现为AB线段上的波峰。不同产地的稻谷外壳在进行拉伸实验过程中AB段的波峰数量会有所差异。从B点之后拉伸载荷下降为零即C点。

2.2 稻谷外壳拉伸破坏前，力-位移参数回归分析

运用MINITAB对曲线OA进行曲线拟合，将稻谷外壳拉伸力和位移数据导入MINITAB数据输入框，设置响应为力，预测变量为位移，回归模型类型为立方型。得到的拉伸力F拉与位移S间的三次回归方程见式(1),方差分析表见表1，拟合曲线结果图见图4。

稻谷外壳拉伸破坏前，力-位移回归方程为

F拉=0.863 7+77.56S+887.2S2-11 410S3

(1)

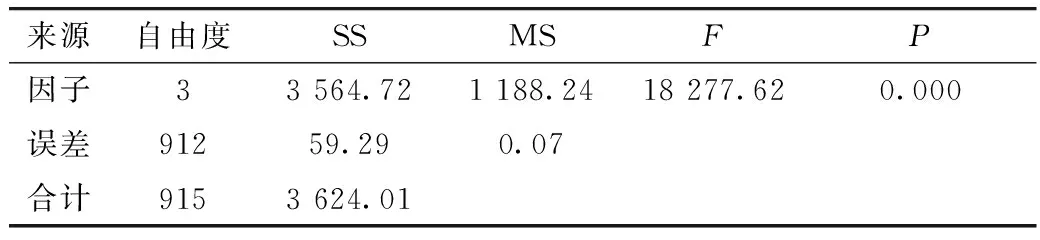
表1 多项式回归分析方差分析表

注：SS为离均差平方和；MS为均方差；F为F统计量；P为显著性概率。

注：S为拟合优度；R-Sq为相关指数；R-Sq(调整)为Minitab调整的相关系数。图4 Minitab拟合曲线结果图

从表1可以看出P=0.000<0.05，表明回归方程是显著的。

从图4可以看出R-Sq=R-Sq(调整)=98.4%，表明建立的回归模型非常可靠。

由分析可知，拟合的三次回归方程可以较为真实反映实验数据的变化规律。

2.3 稻谷外壳拉伸断裂处显微图像分析

利用电子显微镜对拉伸实验过程中的稻谷外壳进行显微分析，进一步对图3中AB段的分析进行验证，拉伸实验前稻谷外壳显微图像如图5所示，可以看出稻谷外壳的纤维呈网状分布，纤维分布密集的区域为沿稻谷长轴方向，但是这些稻谷外壳纤维也呈现明显的差异性，具体表现为纤维粗细、分布不均匀。进行拉伸实验过程中稻谷外壳显微图像如图6所示，在进行稻谷外壳拉伸实验过程中，稻谷外壳总体断裂，但仍然有一部分稻谷外壳纤维没有断裂。进行拉伸实验后稻谷外壳显微图像如图7所示，可以看出稻谷外壳完全断裂，从断裂处可以看出稻谷外壳断裂边缘呈明显的不规则性，断口处还存在已经断裂的稻谷外壳纤维。图6、图7中稻谷外壳的状态可以由图3曲线AB段反映出来。

图6 拉伸实验中稻谷外壳显微图像

图7 拉伸实验后稻谷外壳显微图像

2.4 稻谷外壳拉伸实验数据分析

2.4.1 稻谷外壳拉伸力学参数计算

稻谷外壳的拉伸强度、断裂伸长率、弹性模量、拉伸破坏能等重要的力学属性可通过实验数据计算得出。

拉伸强度计算公式：

(2)

式中：σb为拉伸强度/MPa;P为最大载荷即拉伸破坏力/N;A0为稻谷外壳横截面面积/mm2;b为试样宽度/mm;d为试样厚度/mm。

断裂伸长率计算公式：

(3)

式中：δ为断裂伸长率/%;Δlb为伸长量即拉伸变形量/mm;l0为测量标距即夹具间试样的长度/mm。

弹性模量计算公式：

(4)

式中：E为弹性模量/MPa;ΔP为载荷增量/N;Δl为与载荷增量对应的变形增量/mm。

拉伸破坏能计算公式：

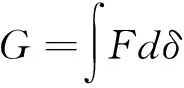
(5)

式中：G为拉伸破坏能/N·mm;F为拉伸力/N;δ为变形量/mm。

2.4.2 稻谷外壳拉伸实验结果

经过对产地为江西、广西、安徽籼稻的稻谷外壳进行拉伸实验可以得到稻谷外壳的力学属性如表2。

表2 稻谷外壳拉伸实验结果

2.4.3 稻谷外壳拉伸实验数据差异显著性分析

运用MINITAB对稻谷外壳的拉伸破坏力和弹性模量进行差异显著性分析。原假设所有样本的均值都相等，备选假设至少有一个均值不同，显著性水平α=0.05，对三个产地的稻谷外壳拉伸实验数据进行单因子方差分析。方差分析结果如表3、表4所示。

表3 不同产地稻谷外壳拉伸破坏力方差分析表

注：AdjSS为调整后的偏差平方和；AdjMS为调整后平均后的偏差平方和,余同。

表4 不同产地稻谷外壳弹性模量方差分析表

从方差分析表3可知P=0.003<0.01，故三个不同产地的稻谷外壳拉伸破坏力具有极其显著的统计学差异。

从方差分析表4可知P=0.004<0.01，故三个产地的稻谷外壳弹性模量具有极其显著的统计学差异。

由分析可知，不同产地的籼稻稻谷外壳的拉伸破坏力和弹性模量存在显著性差异。

3 结论

根据稻谷外壳拉伸断裂裂纹处的显微图像,并结合力-位移曲线进行分析，得出在力-位移曲线达到最大波峰后仍存在几处较小波峰的原因：在进行稻谷外壳拉伸实验过程中，稻谷外壳总体结构断裂后，仍然有一部分稻谷外壳纤维没有断裂。

经过差异显著性分析得出不同产地的籼稻稻谷外壳在拉伸破坏力和弹性模量上存在显著的不同。拉伸破坏力的差异性同样也反映了垄谷机脱壳效率及脱壳率的设备特性；弹性模量的差异性反映了稻谷外壳抵抗变形的能力，在设定的相同实验(或加工)参数时稻谷产生裂纹维数及裂纹扩展方向会有所不同，从而影响到稻谷的破碎程度。

力-位移曲线和回归方程，能较好的反映出稻谷外壳受拉断裂的过程，可对稻谷垄谷、碾白工艺及加工装备的参数优化提供设计支撑。