结合目标估计的自适应压缩跟踪

李国友，张春阳，夏永彬，张凤岭

(燕山大学 工业计算机控制工程河北省重点实验室，河北 秦皇岛 066004)

1 引 言

视频目标跟踪是计算机视觉应用中一个重要的课题，在智能视频监控、虚拟现实、军事领域、人机交互等众多领域有着重要的研究价值.虽然国内外的研究者们对目标跟踪开展了一系列的研究[1]，并取得了一定的成果，但是在实际跟踪中相机抖动、尺寸变化、物体遮挡、动态背景、运动模糊、变形等因素的存在，目标容易漂移和丢失，需要研究人员有待进一步的优化和改进.

经典的目标跟踪算法大体分为三个步骤：目标的外观模型的建立、搜索机制和模型的更新策略[2].外观模型的建立就是利用特征描述目标的过程，在模型建立之前需要特征的选取，由于真实场景的复杂性、目标变化的不确定性和跟踪的实时性，所以选择的特征是以包含目标信息多、区分性强和计算量小为原则，常见的特征有灰度特征、颜色特征、纹理特征、梯度特征等[3]，根据目标外观模型[4]一般可分为：生成式跟踪算法[5-7]和判别式跟踪算法[8-10]；搜索机制是对候选区域的搜索，可分以下几类[2]：基于滤波理论、基于滑动窗口和基于梯度优化的搜索方式；模型的更新策略是在当前帧确定目标之后，对目标的外观做出调整，以适应新的环境，更新方法大多采用每帧更新、隔一定帧数更新或者大于设定阈值更新.Zhang等[10]提出了基于压缩感知理论的CT(Compressive Tracking)跟踪算法，该算法通过稀疏测量矩阵提取前景目标和背景的特征，采用朴素贝叶斯分类器去分类[11].但是在搜索机制中未考虑目标的移动速度，且跟踪的窗口大小是固定的，容易较快的引进误差，从而导致跟踪漂移.侯志强等[12]基于粒子滤波的框架下提出深度稀疏网络的跟踪算法，在复杂环境中具有良好的鲁棒性，但是对于运动模糊，跟踪效果不好.文献[13]提出了对CT改进的自适应压缩跟踪算法(ACT)，通过与样本均值的绝对值大小来调节学习参数以提高稳定性，但对目标的丢失判断假设背景是固定的.

本文针对CT跟踪算法的缺陷，提出了三方面的改进：首先，根据当前帧和先前帧目标区域的相似性，提取前后两帧间目标区域相匹配的特征点，通过建立关系模型实现候选目标的定位；其次，当前帧目标区域中的特征点相对于模板目标区域特征点，若表现的比较离散说明尺度在变大，此时方差较大，反之尺度在变小，方差较小，因此提出了基于匹配点间方差的尺度自适应方法；最后，在遮挡情况下，CT盲目的更新影响跟踪效果，本算法中引入遮挡判断因子，并结合匹配点的数量调整分类器的更新策略，利用遮挡前的目标信息进行目标跟踪，达到抗遮挡的目的.

2 压缩跟踪算法

2.1 随机测量矩阵

根据压缩感知理论，一个S×T维的随机测量矩阵R满足RIP条件，它可以将一个高维图像空间的x(T维)变换到一个低维的空间v(S维)，数学表达式为

v=Rx

(1)

其中S≪T，Zhang等[10]采用了一个非常稀疏的随机测量矩阵，rij表示矩阵中的元素，服从N(0，1)分布，定义为

(2)

其中，Q取值为2或者3.

2.2 特征降维

对每一个样本Z∈Rw×h，将其与一系列多尺度矩形滤波器{h1，1，h1，2，…，hw，h}进行卷积运算.每种尺度的矩形滤波器定义如下：

(3)

式中，i和j分别是矩形滤波器的宽和高，w和h分别是目标图像的宽和高.多尺度图像特征向量维数十分巨大.采用式(2)的稀疏随机矩阵R将x投影到低维空间v.图1是压缩特

图1 压缩特征提取示意图Fig.1 Sketch map of compressed feature extraction

征提取示意图，通过稀疏测量矩阵对这些数量庞大的特征进行压缩，提高运算效率.

2.3 分类器的构建与更新

对于每个样本，它的低维表示是v=(v1，v2，…，vn)T.假定v中的各元素是独立分布的，通过构建朴素贝叶斯分类器[14]对正负样本特征进行分类.

(4)

其中，y=0表示负样本，y=1表示正样本，且假设先验概率相等即P(y=0)=P(y=1).假定在分类器H(v)中的条件概率P(vi|y=0)和P(vi|y=1)也属于高斯分布，

(5)

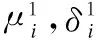
(6)

其中，学习因子λ>0，

(7)

式中，n为正样本个数，vi(k)表示为第k个正样本.同理，负样本的更新方式与其类似.

3 结合目标估计的自适应压缩跟踪算法

3.1 基于ORB算法的运动估计定位

3.1.1 基于ORB算法的目标匹配

在特征点匹配算法中SIFT[15](Scale Invariant Feature Transform)在大多数场景中表现出最好的匹配性能，但花费时间最长，ORB[16](improved oriented FAST and rotated BRIEF)匹配效果是虽然不及SIFT，但是是最快的匹配算法[17].考虑到目标区域的匹配不是匹配点越多越好，还要尽可能的降低非目标区域点的干扰，且跟踪算法对实时性要求较高，因此选用特征点相对稀疏的ORB局部特征匹配.ORB特征点的检测采用的是FAST算法，但是特征点不具有尺度不变性和方向不变性，ORB算法通过构建高斯金字塔，来实现尺度不变性，通过灰度质心法为特征点提供一个主方向：

(8)

式中mpq表示某特征点局部邻域(p+q)阶矩，I(x，y)表示(x，y)坐标的灰度值，C表示灰度质心，θ表示特征点的主方向.ORB特征点的描述采用的是BRIEF描述子，但是BRIEF描述子对噪声敏感和不具备旋转不变性的缺点，ORB算法通过采用优化后的BRIEF描述子(rBRIEF)，解决噪声敏感问题，且具有旋转不变性.匹配方面，用汉明距离代替欧式距离，从而大大减少了匹配时间.目标区域的ORB匹配实现步骤如下：

步骤1.特征点提取.提取先前帧和当前帧中所有特征点.

步骤2.将步骤1中提取的先前帧中的特征点，进行区域的筛选.

步骤3.将先前帧中筛选的特征点和当前帧的特征点进行特征的描述.

步骤4.描述后的特征点进行匹配，并淘汰匹配距离相差较大的匹配点.

目标区域匹配算法如表1所示.

表1 目标区域匹配算法Table 1 Target area matching algorithm

3.1.2 基于关系模型的运动估计定位

图2 运动估计示意图Fig.2 Motion estimation schematic diagram

在视频序列中，将运动目标看做一个整体，特征点在一定程度上呈现整体变化，运动目标呈现出相对平稳的性质，即假设帧间特征点之间的关系是线性的，通过公式(9)将两帧的特征点建立一种对应关系模型.

(9)

其中ax,bx表示特征点横坐标的变换系数，ay,by表示特征点纵坐标的变换系数，cc表示1取到toal的数值.将所有匹配点代入模型得：

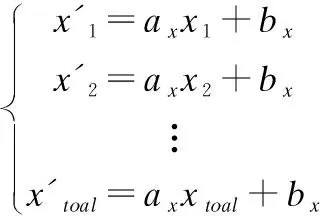
(10)

设误差方程为

(11)

式中

通过最小二乘法原理求解超定方程[18]得到横坐标的变换系数，同理，求解特征点纵坐标的变换系数，这样经过计算就得到了模型变换系数.将第t帧跟踪窗口的左上角点坐标代入建立的特征点对应关系模型，就可以得到t+1帧的候选目标区域.以图3为例，若得到候选目标区域的左上角点为(Xt+1，Yt+1)，则以(Xt+1，Yt+1)为圆心，半径为Rx的圆内搜索候选目标，利用贝叶斯分类器找出最大相应区域，模型的更新以(Xt+1，Yt+1)为圆心，半径为R1的圆内提取新的正样本和半径为(R3-R2)的圆环内提取新负样本进行更新.改进了原算法在以(Xt，Yt)为圆心的区域内搜索候选目标和更新样本的缺陷，从而解决运动速度过快或相机抖动等带来的影响.

图3 目标估计示意图Fig.3 Sketch map of target estimation

3.2 基于方差的尺度自适应

通过研究发现，当两帧目标区域进行ORB匹配时，当前帧目标区域中的匹配点相对于模板目标上的匹配点，如果表现得比较离散，则说明目标尺度在变大，如果表现得比较集中，说明目标尺度在变小.

在数学中，方差反映了数据的离散程度，于是本文提出了基于匹配点间方差的尺度自适应.此外，点在平面中代表的是二维信息，方差反映的是一维数据的离散程度，且目标在宽和高方面的尺度变化是独立的，于是将点的位置坐标看做两个独立的一维空间.具体实现如下：先以横坐标方向上变化为例，先分别求出模板目标和当前目标所有特征点横坐标方向上的方差Dfront-x和Dcurrent-x.

(12)

E(·)表示·的期望值，然后式(13)求出横坐标方向上变化幅度，最后通过式(14)确定横坐标方向上的最终尺度.

(13)

Wcurrent=Wfront×(1+α×WS)

(14)

式中，α表示调节的参数，WS表示水平方向增加或者减少的幅度，Wfront和Wcurrent分别表示先前目标和当前目标的宽度.同理，

Hcurrent=Hfront×(1+β×HS)

(15)

β表示调节的参数，HS表示垂直方向增加或者减少的幅度，Hfront和Hcurrent分别表示先前目标和当前目标的高度.

3.3 遮挡判断因子和特征点数目在调整分类器中的应用

压缩跟踪算法在遮挡时的不足主要体现在两方面：一方面是只记得前一帧的目标特征信息，没有使用先前帧的信息，另一方面是每帧都更新分类器的盲目性.本文引入遮挡判断因子并结合匹配点的数量进行遮挡判断，并以匹配点数量调整分类器的更新策略，利用历史帧目标信息跟踪目标.

选用Bhattacharyya距离计算匹配模板目标区域与当前帧目标区域的颜色直方图相似度，此方法的优点是直方图容易归一化且计算量小，适合大小不同的图像.为了避免亮度的影响，先将图像转化到HSV颜色空间中，计算出H-S直方图，然后归一化求取相似度.Bhattacharyya距离可以表示为：

(16)

(17)

本文采用dBhattacharyya(H1，H2)作为遮挡判断因子，其值越大，相似程度越小，反之，越大，具体规则定义为

其中λT表示遮挡阈值.由于Bhattacharyya距离判断遮挡的

图4 更新部分流程图Fig.4 Update part flow chart

发生是不稳定的，而经过进一步研究可知，当两幅图像中相似的角点数量较多时，也存在着较高的相似度，于是本文综合这两方面进行遮挡的判断.

根据在遮挡前后目标区域信息经历从多变到少再到多的变化，匹配点的数量也会经历由多变少再到多的过程，本文引入了判断因子和匹配点阈值进行遮挡的判断，在遮挡后用ORB算法将匹配模板目标信息与当前帧目标区域相匹配，有针对性的搜索候选目标，且用遮挡前更新的分类器进行分类，能很好的跟踪遮挡干扰下的目标.具体实现过程如图4所示：用遮挡因子判断是否发生遮挡，如果不发生遮挡，此时重新提取样本及特征、更新分类器和更新匹配模板的目标信息；如果发生遮挡，此时要保留匹配模板的目标信息，在下一帧判断匹配点数是否达到设定阈值，如果达到，说明不是真正的遮挡，将继续执行更新部分，否则，确实发生了遮挡，用模板匹配帧的目标信息一直与当前帧的目标区域相匹配，直到匹配点达到设定阈值才进行算法的更新部分.

4 实验步骤

输入：初始帧中表示目标的矩形区域，正样本采集半径α，负样本采集半径大于ζ小于β的圆环，候选目标搜索半径Rx，设定的匹配点数量阈值.

输出：第t帧图像的目标位置，分类器的参数，两帧间目标区域的Bhattacharyya距离和匹配点的数量.

步骤1.手工的标记须要跟踪的矩形区域.

步骤2.依据积分图和所得的Haar特征提取模板，提取正负样本的特征.

步骤3.更新贝叶斯分类器，获取新的分类器.

步骤4.通过ORB进行特征匹配，利用帧间匹配点的坐标建立模型，进行样本的估计定位.

步骤5.利用特征点间的方差进行尺度的自适应.

步骤6.在半径Rx范围内提取定位后的新(正)样本，并通过产生的Haar特征提取模板，计算积分图作为当前帧正样本的特征.

步骤7.贝叶斯分类器对这些待分类区域对进行分类，选出最有可能是目标的矩形框，作为当前跟踪结果.

步骤8.使用Bhattacharyya距离和匹配点的数量约束分类器的更新(详见遮挡处理部分).

步骤9.转入步骤4，直到循环结束.

5 实验结果及分析

5.1 实验数据及平台

为了验证本文算法的有效性，视频序列均来自Benchmark网站上的标准测试序列，这些序列存在尺度变化、快速运动、运动模糊、遮挡、非刚体变形等干扰，与当期经典的跟踪算法进行实验对比，这些算法包括：ACT[13]、MIL[19]、Struck[20]、CT[10]、LOT[21]、KCF[22]，并从中心位置误差、跟踪重叠率和跟踪成功率三个方面进行定性与定量评价.本文算法的实现是在Windows7操作系统下，采用Matlab 2015+opencv2.4.11作为软件平台，计算机配置为Intel CPU 3.3 GHz处理器和4.0 GB内存.本算法的主要参数设置如下：正样本的搜索半径为8，表示前一帧目标周围8个像素范围内搜索正样本，负样本的搜索半径为12到30的圆环，并随机选择的负样本个数为50，候选目标的搜索半径为20，大约生成1100个样本，投影空间的维数为50，学习速率为0.8.如表2不同算法在测试序列中的平均帧率.

表2 跟踪算法的平均帧率Table 2 Average frame rate of the tracking algorithm

5.2 结果对比分析

5.2.1 定量分析

本文使用三种标准来综合评价跟踪算法的性能

1)中心位置误差(CLE)，定义为

(18)

其中(xT，yT)表示真实跟踪的目标中心位置，(xG，yG)表示标准跟踪的目标中心位置，距离越小则误差越小，跟踪精度越高.

2)重叠率(OR)，定义为：

(19)

其中ROIT表示真实的跟踪窗口，ROIG表示标准的跟踪窗口，OR值越大表示实际的跟踪情况越接近标准.

3)成功率(SR)，成功率是建立在重叠率基础上，文献[23]认为如果OR>0.5，则表示本帧跟踪成功，成功率是成功跟踪的帧数与总序列帧数的比值.

图5 不同序列的中心误差变化曲线图Fig.5 Central error variation curve of different sequences

图5黑色实线是本文算法在不同序列的中心误差曲线，首先在测试序列中Girl2和Jogging序列达到最小误差；除Dog1序列的其它序列，本文算法表现出相对较小误差，有时误差会稍大于KCF或者Struck，但整体来看，本文算法相比其他算法表现出较小的误差；虽然Dog1序列在中心误差标准中本文算法误差较大，但通过跟踪效果图和成功率可知，除LOT外，对比算法都没有明显尺度变化，所以在该序列中效果最好的是LOT，本文算法次之.

表3 跟踪算法的平均重叠率Table 3 Average overlap rate of the tracking algorithm

表3是7种算法在8个图像序列中的平均重叠率.原算法CT在所选取的测试视频中的平均重叠率是0.40，经过文献13改进的CT重叠率为0.41，经过改进的本文算法的平均重叠率是0.62，与原算法相比，得到了很大的改进，且从表3可知高于其他算法的平均重叠率.表4是7种算法在8个图像序列中的成功率，通过表4可以看出成功率最高的是本文算法，其次是KCF和Struck，接着是ACT、CT、MIL和LOT.综合以上分析和实验结果，表明了本文算法具有较高的成功率和较好的跟踪效果.

表4 跟踪算法的平均成功率Table 4 Average success rate of the tracking algorithm

5.2.2 定性分析

图6展示了不同算法在测试集上的跟踪结果，从上到下依次是BlurCar2、BlurFace、Couple、David、Dog1、Girl2、FaceOcc1和Jogging序列，其中左上角白色数字代表视频帧的序数，黑色实线框代表本文算法结果.本节定性地对比分析算法在不同场景中的跟踪效果.

1)快速运动及其运动模糊

以BlurFace序列为例，在#175和#263帧时，对比算法出现了不同程度的漂移，本文算法和KCF能够准确跟踪，在#299帧，CT有所改善，但是在#380帧和#405帧又开始漂移，在此序列中，CT、ACT、MIL、和LOT和Struck漂移很大，无法完成跟踪任务，只有本文算法和KCF在快速运动及模糊情况下能很好的实现跟踪.

图6 不同算法的部分跟踪结果Fig.6 Partial tracking results of different algorithms

2)尺度自变化

选中的测试集中跟踪窗口都是变化的，但是表现比较突出的是David和Dog1序列.以Dog1序列为例，在#172帧中ACT出现漂移，其他算法基本可以实现跟踪任务，在接下来的#251、#434、#533和#720帧中，LOT和本文算法表现出很好的尺度性，虽然其他算法与标准中心具有很小的距离误差，但综合尺度因素，LOT效果最好，本文算法次之.

3)全局遮挡及局部遮挡

FaceOcc1序列属于半遮挡，Girl2和Jogging序列是全局遮挡.以Jogging序列为例，遮挡之前(#56帧)，LOT和ACT出现了漂移，但发生遮挡之后(#83)，只有本文算法和ACT能进行目标的跟踪，在#128、#197和#264帧中，ACT又出现了漂移，并且从#128和#197中也可以看出很好的尺度性.

4)背景干扰

对于Couple序列，存在着背景干扰、尺度变化、快速运动等多个干扰信息，在#68帧中KCF出现严重漂移，完全脱离目标，LOT稍有漂移，在#91帧时，只有本文算法能实现跟踪，其他对比算法受背景、快速运动、尺度等的干扰，全部发生漂移，丢失跟踪目标，在#97帧和#115帧只有本文算法和Struck能锁定目标，但是Struck漂移很大，且尺度性没有本文算法好.

6 结 论

针对传统压缩跟踪算法的缺陷，本文通过帧间目标区域匹配点的关系模型进行候选目标的位置估计，解决原算法搜索区域受运动速度的影响；提出了基于特征点间方差的尺度自适应方法，解决了原算法固定大小跟踪窗口的不足；此外引入遮挡判断因子和匹配点的数量进行遮挡判断，并以匹配点的数量为条件更新分类器，利用历史帧目标信息解决遮挡问题，最终很好的实现了算法的优化与改进.为了验证本算法的有效性，选取公共数据集上八个测试视频序列，与当前经典跟踪算法进行对比，实验结果表明本文所提出的算法具有更好跟踪效果，对目标跟踪中的相机晃动，快速运动、尺度变化、遮挡等因素具较好的抗干扰能力，并且可以满足实时性要求，具有很好的实用价值.