延迟代价双量化三支决策
徐健锋,苗夺谦,张远健
1(同济大学 电子与信息工程学院,上海 201804) 2(南昌大学 软件学院,南昌 330047) 3(嵌入式系统与服务计算教育部重点实验室(同济大学),上海 201804) 4(江西省经济犯罪侦查与防控技术协同创新中心,南昌 330031)
1 引 言
三支决策(Three-way Decisions)[1]是在粗糙集基础上发展的一种不确定问题求解的理论.其主要思想是通过引入延迟决策,将决策论域一分为三,使得具有相对充分信息的对象集合被快速分类,而信息相对不确定的对象集合则作为延迟决策区域等待进一步区分.近几年三支决策在垃圾邮件过滤[2]、文本情感[3,4]、图像识别[5]、流计算[6]等应用领域都取得了显著的成果.
决策粗糙集理论[7]是三支分类求解的最经典理论之一.其主要思想是在概率粗糙集模型基础上通过引入贝叶斯决策理论,建立基于决策代价损失关系基础上,各区域总体决策风险最小化的模型,并且给出了基于代价敏感的三支决策阈值求解的计算公式.代价敏感三支决策相关研究成果包括不同数据模型的决策粗糙集推广.例如,基于代价敏感度量的概率粗糙集三支决策[8,9]、模糊集三支决策[10]、区间集三支决策[11]、邻域三支决策[12]等.其它相关研究成果还包括:文献[13]将当前决策粗糙集研究的决策偏好从单纯的风险扩充到以时间、金钱为度量的测试代价,并建立了序独立测试代价敏感信息系统.文献[14]进一步研究了以测试代价最小为目标的属性约简问题.文献[15]结合测试代价和误分类代价,提出了一种新的代价敏感决策粗糙集模型.文献[16]进一步研究了决策粗糙集的动态计算等.
上述研究显示决策粗糙集丰富的发展活力.双量化具有完备刻画粗糙集近似空间的重要功能.决策粗糙集理论提出了正域元素和负域元素被划分到三支决策域的一组代价域值及其损失函数风险最小化决策的推理,文献[17]则将经典多粒度及双量化研究与决策粗糙集进行了结合研究.但是,其研究内容也基本上都是基于经典的六个决策代价函数展开研究的.而.通常三支决策应用中,存在不确定的对象进行延迟决策的代价一般比任何正域或负域较确定的对象决策代价都要低的现象,而这种现象是无法用决策粗糙集中的简单单调递增或单调递减的延迟代价函数表示的,这种问题可以通过多重代价函数的方式表达,而三支决策的代价函数的双量化及其三支决策目前尚未展开研究.
本研究首先提出了一种基于三支决策损失函数间逻辑关系的阈值计算方法.其次,根据现实应用中普遍存在的决策延迟域代价目标函数非单调的现象,提出延迟损失函数双量化的二种典型分布模式,其乐观、悲观三支决策的阈值推导方法.最后,通过一组典型的实例证明了上述代价双量化三支决策的阈值计算方法及三支决策分类的推理是有效的.
2 相关工作
概率粗糙集是构造三支决策的基础原型之一,也是决策粗糙集的基础[18,19].经典信息系统IS是概率粗糙集的基础数据模型,其通常可以被形式化为一个四元组IS=(U,A,V,f).其中U代表论域中的对象集合,A=C∪D代表属性集合(C是条件属性,D是决策属性),V代表属性的取值范围,f代表从对象到属性取值的信息函数,即f:U×A→V.
为了简化讨论,本文假定信息系统是完备的,即所有对象的所有属性取值都是已知的.本文以等价关系为例,首先回顾经典决策粗糙集的代价分析[7-9],然后讨论代价敏感三支阈值的求解.
2.1 经典决策粗糙集
定义1.(等价关系)给定信息系统IS上的属性子集B,满足条件B⊆A,则基于属性B的等价关系记为:
IND(B)={(x,y)∈U×U|∀a∈B,f(x,a)=f(y,a)}
(1)
处于同一个等价类的任一对象集合[x]构成了信息粒的基本结构.从概率论角度可以刻画对象x∈U对某个决策类Di∈U/IND(D)的隶属程度.定义如下.
定义2.(条件概率)对象x∈U相对于决策类Di∈U/IND(D)的隶属程度被定义为对象所属等价类 [x]R对决策类Di的条件概率,记为Pr(Di|[x]R),其计算公式为
(2)
基于概率粗糙集理论,在条件概率和等价类定义的基础上,任意决策类的不确定程度可以由上下近似的方式表示.定义如下:
定义3.(三支决策规则)给定一对阈值(α,β),满足0≤β<α≤1,则信息系统IS中决策规则[x]R→Di的三支决策定义为:正域(POS(α,·)(Di))、边界域(BND(α,β)(Di)) 和负域(NEG(·,β)(Di)).其中:
POS(α,·)(Di)={x∈U|Pr(Di|[x]R)≥α}
BND(α,β)(Di)={x∈U|β
(3)
决策粗糙集[20]在概率粗糙集理论的基础上引入了最小风险贝叶斯决策理论.三支决策理论本质上是通过找到一对最小期望风险的阈值(α,β),对问题域进行三支决策,决策结果将问题域划分为POS域、NEG域和BND域,并且对应着不同的风险或利益[21-23].其中,决策对象集X的三支决策区域可记为:POS(α,·)(X),BND(α,β)(X),NEG(·,β)(X).
基于贝叶斯风险理论,不同决策显然会产生不同的损失.设λPP,λPN表示为正域元素和负域元素分别被划分为正域的代价函数;λNP,λNN表示为正域元素和负域元素分别被划分为负域的代价函数;λBP,λBN表示为正域元素和负域元素分别被划分为延迟域的代价函数.当任一对象x∈U的等价类[x]R被分别划分至三个支决策域后,其三支决策代价目标函数可以分别表示为:正域决策代价目标函数TP,负域决策代价目标函数TN,延迟决策代价目标函数TB.即:
TP=λPPPr(X|[x]R)+λPNPr(X|[x]R)
TN=λNPPr(X|[x]R)+λNNPr(X|[x]R)
TB=λBPPr(X|[x]R)+λBNPr(X|[x]R)
(4)
其中Pr(X|[x]R)+Pr(X|[x]R)=1
而三支决策整体期望目标[24]可以表示为:
(5)
TP=(λPP-λPN)Pr(X|[x]R)+λPN
TN=(λNP-λNN)Pr(X|[x]R)+λNN
TB=(λBP-λBN)Pr(X|[x]R)+λBN
(6)
根据贝叶斯决策准则,每个对象等价类都需要选择期望损失最小的行动集作为最佳行动方案,于是可以得到如下三条决策规则:
TP≤TN∧Tp≤TB→x∈POS(α,β)(X)
TB≤TP∧TB≤TN→x∈BND(α,β)(X)
TN≤TP∧TN≤TB→x∈NEG(α,β)(X)
(7)
假设损失函数满足:λNP≥λBP≥λPP≥0,λPN≥λBN≥λNN≥0 ,将式(6)中的代价目标函数TP、TN、TB分别代入上述三条决策规则,则三条决策规则可直接推导出:
Pr(X|[x]R)≥α→x∈POS(α,β)(X)
β
(8)
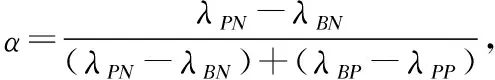
可以观察到这三个域的代价目标函数TP,TN,TB的几何含义是以Pr(X|[x]R)为变量,相关代价函数组合为斜率和截距的线性函数.例如:损失函数TP是以正域相关代价目标函数组合λPP-λPN为斜率λPN为截距的线性函数.损失函数TN是以负域相关代价目标函数组合λNP-λNN为斜率λNN为截距的线性函数.损失函数TB是以不确定域相关代价目标函数组合λNP-λNN为斜率λNN为截距的线性函数.
如图1 之间的关系示意图所示,三支分类的阈值(α,β),可以看作是上述三个代价目标线性函数之间直线交集的横坐标Pr(X|[x]R)取值.其三支划分的目标为:
Pr(X|[x]R)取值根据α划分后的TP和TB的代价目标函数取值是相对最低的;
Pr(X|[x]R)取值根据β划分后的TN和TB的代价目标函数取值是相对最低的;
显然,α,β的取值可以看作是线性函数TP与TB及TN与TB交点的Pr(X|[x]R)处取值.而本文把目标函数TN与TP间交点的Pr(X|[x]R)取值:
被定义为γ,其语义为三支决策退化为二分类的阈值.所以T(α,β)退化为二支决策时也可以表示为T(γ,γ).
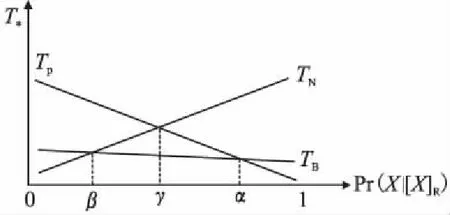
图1 TN,TP,TB之间的关系示意图Fig.1 Illustration for relationship within TN,TP,TB
2.2 代价目标函数及其阈值分析
基于三个域的代价目标函数TP,TN,TB的代数及几何含义,可以从代数角度出发,基于三支局部结构求解目标阈值[24]:
通过求解如下以Pr(X|[x]R)为自变量的决策代价目标函数TP,TB构成的代价目标函数方程组:
(9)
代入TP=TB可得:
可以观察发现上述求解TP=TB获得的Pr(X|[x]R)取值与经典决策粗糙集理论中指定的α取值形式上是一致的,所以本文也将其记为α.根据线性函数TP=TB的几何含义可以得到如下关于α取值与决策代价之间的性质.
性质1.当λPP-λPN<λBP-λBN时,可得:
α≥Pr(X|[x]R)≥0⟹TP≥TB
证明:由于其中代价目标函数TP可以看作是以Pr(X|[x]R)为自变量,λPP-λPN为斜率的一元线性函数.代价目标函数TB也可以看作是Pr(X|[x]R)为自变量,λBP-λBN为斜率的一元线性函数.线性函数TP和TB之间的线性关系图如图2(a)所示:

注:图2-图8所示的代价目标线性函数关系示意图中,横坐标为Pr(X|[x]R)取值,纵坐标为决策代价目标函数T*(其中*∈{B,P,N})的取值.
性质2.当λPP-λPN>λBP-λBN时,可得:
α≥Pr(X|[x]R)≥0⟹TP≤TB,或α≤Pr(X|[x]R)≤1⟹TP≥TB.
证明:当λPP-λPN>λBP-λBN时,TP,TB之间的关系如图2(b)所示.其证明过程与性质1证明相似.
通过求解如下TN,TB构成的代价目标函数方程组

代入TN=TB:可得
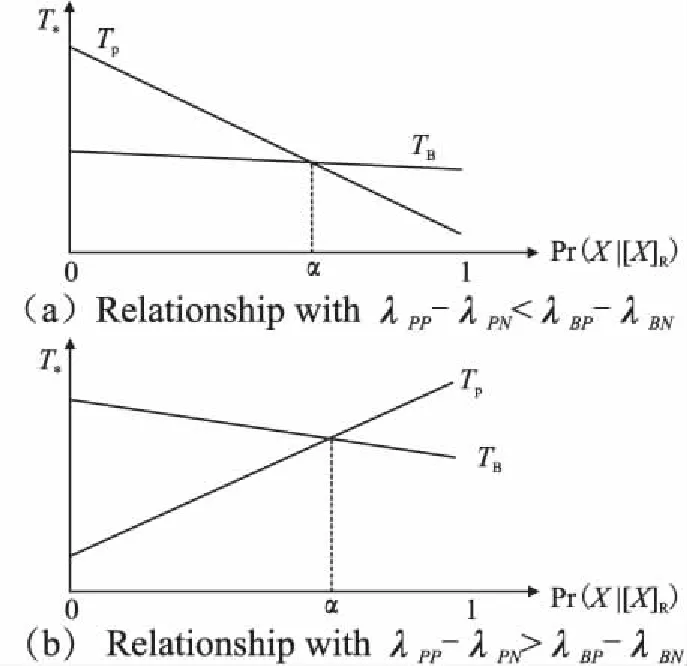
图2 代价目标函数TP,TB之间的关系图Fig.2 Relationship between the cost objective function TP and TB
可以观察发现求解TN=TB获得的Pr(X|[x]R)取值与决策粗糙集理论中指定的β取值形式上是一致的,所以本文也将其记为β.根据TN=TB的几何含义可以得到如下关于β取值与决策代价之间的性质.
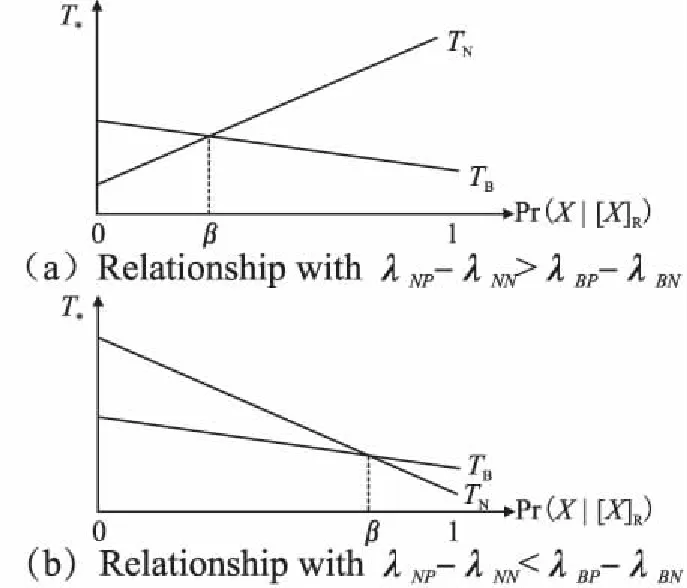
图3 代价目标函数TN,TB之间的关系图Fig.3 Relationship between the cost objective function TN and TB
性质3.当λNP-λNN>λBP-λBN时,可得:
β≥Pr(X|[x]R)≥0⟹TB≥TN
性质4.当λNP-λNN<λBP-λBN时,可得:
β≥Pr(X|[x]R)⟹TB≤TN
性质5.当λPP-λPN<λNP-λNN时,可得:
γ≥Pr(X|[x]R)≥0⟹TP≥TN
性质6.当λPP-λPN>λNP-λNN时,可得:
γ≥Pr(X|[x]R)≥0⟹TP≤TN
上述性质证明如下:
性质3证明:当λNP-λNN>λBP-λBN时,TN,TB之间的关系如图3(a)所示,其证明过程与性质1证明相似.
性质4证明:当λNP-λNN<λBP-λBN时,TN,TB之间的关系如图3(b)所示,其证明过程与性质1证明相似.
性质5证明:其证明过程与性质1证明相似.
性质6证明:其证明过程与性质1证明相似.
由上述研究可知在决策粗糙集理论中,代价目标函数TP、TB、TN都是典型的单调线性函数.
3 延迟域代价目标函数的双量化

例如高考录取工作中,分数远高于录取分数线的同学与分数远低于录取分数线的同学被延迟录取的风险都较大.而分数处于录取分数线附件的同学,由于其不确定性最强,被延迟录取的代价往往是最低的.

显然经典决策粗糙集理论,无法直接解决类似上述背景的复杂不确定决策情况.采用延迟域代价双量化是解决上述矛盾的有效策略.
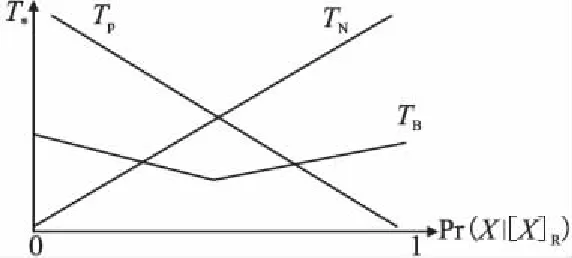
图4 非单调性TB与单调性TP及TN之间的关系示意图Fig.4 Illustration of Non-monotonic TB against monotonic TP and TN
由于双量化不但具有完备刻画粗糙集近似空间的重要功能,而且是粒计算思想的体现.根据1.2节讨论的延迟域代价目标函数非单调现象,采用延迟域代价双量化方法是解决上述矛盾的有效策略.
其主要思想,非单调性TB可以看做是由二个经典延迟代价目标函数组合而成.如图4所示,非单调性TB的拐点,可看作是二个单调延迟代价目标函数的交点,具体讨论如下.

(10)

(11)
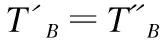

实际上,由于边界域的特性,确定边界域的形态即可确定三支的形态.因此,下文给出基于正负域视角的延迟代价乐观(悲观)双量化阈值,如定义5和定义6所示.
定义5.基于正负域视角的延迟代价乐观双量化阈值.当λNP-λNN>0并且λPP-λPN<0时,乐观三支决策的正域的决策阈值为min(α′,α″),负域的决策阈值为max(β′,β″).
定义6.基于正负域视角的延迟代价悲观双量化阈值.当λNP-λNN>0并且λPP-λPN<0时,乐观三支决策的正域的决策阈值为max(α′,α″),负域的决策阈值为min(β′,β″).
根据定义5和定义6,我们可以得到基于正负域视角的延迟代价乐观(悲观)双量化的三支形态,如定理1、定理2所示.

Pr(X|[x]R)≥α″→x∈POS(α,β)(X)
β′ Pr(X|[x]R)≤β1→x∈NEG(α,β)(X) (12) 根据定义6可以判定乐观三支决策的正域的决策阈值为α″,负域的决策阈值为β′. 根据性质1、性质3 和性质5,易证: 图5 基于延迟代价双量化三支决策模型1 Fig.5 Three-way decisions based on double-quantification with deferment:Model 1 Pr(X|[x]R)≥α′→x∈POS(α,β)(X) (13) 证明:定理2所述延迟代价双量化三支决策模型 如图4所示,证明过程与定理1证明过程类似. Pr(X|[x]R)≤α′→x∈POS(α,β)(X) (14) 证明:定理3所述延迟代价双量化三支决策模型如图5所示,证明过程与定理1证明过程类与定理1证明过程类似.此处略. 图6 基于延迟代价双量化三支决策模型2 Fig.6 Three-way decisions based on double-quantification with deferment:Model 2 Pr(X|[x]R)≤α″→x∈POS(α,β)(X) (15) 证明:定理4所述延迟代价双量化三支决策模型如图6所示,证明过程与定理1证明过程类与定理1证明过程类似.此处略. 上述基于三支决策代价目标函数间逻辑关系的阈值求解方法,可通过一个简单的实例进行说明.如表1所列,给定了等价类相对于概念X归属的概率信息表[25],由15个等价类组成.其中[x]i表示第i个等价类,Pr([x]i)表示样本属于[x]i的概率,Pr(X|[x]i)表示确定等价类[x]i属于概念X的条件概率. 表1中只记录了以X为决策值的各个决策规则条件概率取值情况,根据X与X之间的互补性可以推导出以X为决策值的各个决策规则条件概率取值情况,即Pr(X|[x]i)=1-Pr(X|[x]i).随机选取二具有代表性的代价函数值,其设定如表2所示.分别用代价模式1,2代表不同的双量化代价目标函数组合.同时为了简化讨论本实例约定决策阈值取值范围是0≤β<0.5<α≤1或者1≥β>0.5>α≥0. 本实例基于表1提供的Pr(X|[x]i)取值信息,通过2.2节提出的代价目标函数方程组求解三支决策阈值.再根据第3章提供的定理求解不同代价目标函数取值模式下各个三支决策阈值的语义及三支分类. 根据定义4及性质1-性质2,通过计算表2提供的代价模式1可以获得 α′=0.8,α″=0.63,β′=0.36,β″=0.2,μ=0.5 1)由于代价模式1满足定理1的条件,所以表2中满足Pr(X|[x]i)≤3.6的对象为乐观三支决策负域,满足Pr(X|[x]i)≥0.63的对象为乐观三支决策正域,满足0.36 根据上述阈值对表2中实验对象数据实施三支分类,得到三支决策域划分为: POS(α,β)(X)={[x]1,[x]2,[x]3,[x]4,[x]5,[x]6,[x]7} BND(α,β)(X)={[x]8,[x]9,[x]10} NEG(α,β)(X)={[x]11,[x]12,[x]13,[x]14,[x]15} 2)由于代价模式1满足定理2的条件,所以表2中满足Pr(X|[x]i)≤0.2的对象为悲观三支决策负域,满足Pr(X|[x]i)≥0.8的对象为悲观三支决策正域,满足0.2 POS(α,β)(X)={[x]1,[x]2,[x]3,[x]4,[x]5,[x]6,[x]7} BND(α,β)(X)={[x]8,[x]9,[x]10,[x]11} NEG(α,β)(X)={[x]12,[x]13,[x]14,[x]15} 根据定义4及性质1-性质2,通过计算表2提供的代价模式2可以获得: β′=0.8,β′′=0.63,α′=0.36,α′′=0.2,μ=0.5表1 实例概率信息[25]Table 1 Probabilistic information of the instance 3)由于代价模式2满足定理3的条件,所以表2中满足Pr(X|[x]i)≤3.6的对象为乐观三支决策负域,满足Pr(X|[x]i)≥0.63的对象为乐观三支决策正域,满足0.36 表2 代价目标函数表Table 2 Values of cost objective function 对象数据实施三支分类,得到三支决策域划分为: POS(α,β)(X)={[x]11,[x]12,[x]13,[x]14,[x]15} BND(α,β)(X)={[x]8,[x]9,[x]10} NEG(α,β)(X)={[x]1,[x]2,[x]3,[x]4,[x]5,[x]6,[x]7} 4)由于代价模式2满足定理4的条件,所以表2中满足Pr(X|[x]i)≤0.2的对象为悲观三支决策负域,满足Pr(X|[x]i)≥0.8的对象为悲观三支决策正域,满足0.2 POS(α,β)(X)={[x]12,[x]13,[x]14,[x]15} BND(α,β)(X)={[x]8,[x]9,[x]10,[x]11} NEG(α,β)(X)={[x]1,[x]2,[x]3,[x]4,[x]5,[x]6,[x]7} 基于表2代价模式1和代价模式2的延迟代价双量化三支决策示意图如图7和图8所示.上述实例及其相关三支决策较好的解决了图4所示的延迟代价目标函数的单调不一致的现象. 图7 基于表2代价模型1的延迟代价双量化三支决策示意图Fig.7 Illustration of double-quantification with deferment based on cost model 1 in Table 2 图8 基于表2代价模式2的延迟代价双量化三支决策示意图Fig.8 Illustration of double-quantification with deferment based on cost model 2 in Table 2 本研究对经典决策粗糙集理论中延迟代价目标函数双量化后的的各种复杂三支决策逻辑关系进行了讨论.构造了基于双量化代价目标函数间逻辑关系的阈值求解模型,并且拓展了种双量化延迟损失函数取值情况下的三支分类乐观与悲观决策的推导方法.通过实例证明了上述研究提供了一种更加灵活的决策粗糙集三支分类方法,是代价敏感三支决策的理论扩展. 在实际应用中各种复杂的双量化决策代价目标场景都可能遭遇.比如群体决策中,不同决策者具有不同的复杂风险偏好(如理财投资),甚至有可能有非完全理性的感性偏好.这些不同应用场景中的更加复杂的多量化代价目标函数关系是本研究后续的重要工作.





β″
α′

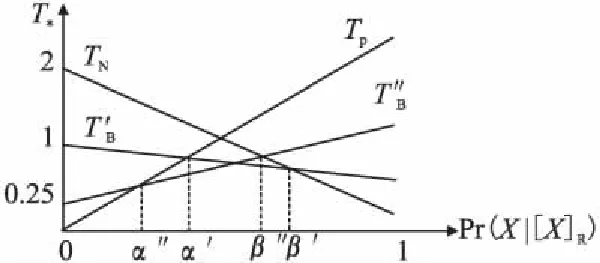
α″4 代价双量化三支决策实例



5 结束语

