基于准平衡滑翔的解析再入制导方法

王肖， 郭杰， 唐胜景， 祁帅

(北京理工大学 宇航学院, 北京 100081)

0 引言

高超声速滑翔飞行器具有速度快、机动能力强、射程远、精度高等特点，受到世界各国的持续关注[1-2]，再入制导一直是其研究难点。再入制导方法分为标准轨迹制导和预测校正制导两类：标准轨迹制导需要离线设计飞行器的标准轨迹，并在线跟踪标准轨迹得到制导指令[3]，该方法实现简单、在线计算量小，但依赖于标准轨迹，易受扰动影响，也不利于轨迹的在线规划；预测校正制导不依赖于标准轨迹，根据在线预测终端值与期望值的偏差实时校正制导指令，预测校正制导对初始误差和参数摄动具有较强的鲁棒性，实时性较好。随着再入任务对自主性、鲁棒性要求的提高，预测校正制导逐渐成为再入制导发展的趋势[4]。

文献[5]通过数值预测建立攻角、倾侧角与纵程、横程之间的线性关系，进而校正控制量。文献[6-10]将过程约束转化为倾侧角幅值约束，然后利用倾侧角剖面预测终端待飞航程，并校正倾侧角指令。文献[11-12]设计了两种分段预测校正制导算法，利用预设航路点将轨迹分段预测，提高了计算效率，但该方法依赖于离线优化，并降低了算法的自主性。文献[4,13-14]设计并改进了一种适用于各类升阻比飞行器的数值预测校正制导算法，以航程误差校正倾侧角剖面作为基准算法，辅以高度变化率反馈以满足过程约束。然而，上述方法均属于数值预测校正制导，需要不断在线数值积分，对弹载计算能力的要求较高，无法广泛应用。

相比之下，解析形式的预测校正制导避免了对弹道的数值积分，计算量大幅减少，更有利于弹上实现。文献[15]研究了零攻角条件下动能弹头的解析预测制导，但并不适用于高超声速滑翔飞行器。文献[16-17]研究了跳跃式再入返回的解析预测校正制导，仅适用于低升阻比飞行器。文献[18]将升力系数分为3个分量，实现了纵向运动方程、横向运动方程和速度方程的解耦，求得了滑翔轨迹的解析解，但仍需数值积分。文献[19]将过程约束转化为高度- 速度平面内的统一解析式，并给出了可重复使用运载器的闭环解析解，但该方法本质上属于标准轨迹生成方法。文献[20]以常值升阻比得到了倾侧角和待飞航程之间的解析关系，但不能保证准平衡滑翔条件，也未对终端高度进行严格约束。

现有的预测校正制导一般考虑终端能量和航程约束，但约束终端能量并不能严格约束终端高度。文献[21]将攻角、倾侧角作为控制量，每个制导周期根据终端航程、高度误差的加权函数更新控制量剖面，有效减小了终端高度误差，但该方法仍需数值预测轨迹，在线计算量较大。

此外，如何保证过程约束也一直是预测校正制导的难点，传统方法一般利用准平衡滑翔条件将过程约束转化为倾侧角走廊[6,22]。然而，再入过程中准平衡滑翔条件不一定严格成立，且实际飞行中的大气环境扰动和飞行器参数的不确定性也使得这种倾侧角走廊的可靠性难以保证[23-24]。

基于上述分析，本文提出了一种基于准平衡滑翔的解析制导方法。首先基于常值升阻比假设建立了再入航程与倾侧角的解析关系，得到了倾侧角指令。然后针对终端高度约束，利用常值航迹角假设建立了终端高度与航迹角的解析关系，得到了航迹角指令，进而通过设计反馈控制律求得攻角指令。对于过程约束，提出了一种在线约束控制方法，将过程约束问题转化为航迹角指令跟踪问题。最后，通过数值仿真表明该方法计算速度快、精度较高，且较好地满足各种约束。

1 制导问题描述

1.1 运动方程

高超声速滑翔飞行器的三自由度运动方程一般以时间为自变量[3]，但由于飞行时间无法事先确定，给弹道积分造成一定困难。为此，本文引入如下能量形式的无量纲变量：

(1)

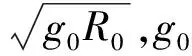
(2)

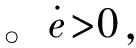
(3)

式中：λ和φ分别为地球经度和纬度；θ为航迹角；ψ为航向角；σ为倾侧角；L为无量纲升力加速度。L和D的计算公式可表示为

(4)

式中：m为飞行器质量；S为飞行器特征面积；CL和CD分别为升力和阻力系数，且是攻角α和速度v的函数；ρ为大气密度，

ρ(h)=ρ0e-h/hs，

(5)

ρ0为海平面大气密度，h为无量纲高度，hs=7 110/R0为高度系数。

1.2 再入约束

再入约束一般可分为过程约束和终端约束。典型的过程约束包括热流密度约束、过载约束和动压约束，其计算公式分别为

(6)

(7)

(8)

终端约束一般包括终端高度约束、速度约束及经度、纬度约束。由于运动方程以能量为自变量，于是终端约束可表示为

(9)

s(ef)=sf，

(10)

式中：s(ef)为无量纲终端再入航程；sf为再入航程的实际值。s(ef)与sf计算公式分别如(11)式和(12)式所示：

(11)

sf=arccos (sinφ0sinφf+cosφ0cosφfcos(λf-λ0))，

(12)

式中：λ0、φ0为飞行器初始经度和纬度。

2 制导算法

2.1 倾侧角解析解

初始下降段飞行高度较高，气动力作用较弱，通常通过迭代得到常值倾侧角进行开环制导，并当满足一定条件后转入滑翔段[6,22]。

对于滑翔段制导，考虑终端航程约束及(11)式，再入过程中，特别是满足准平衡滑翔条件(QEGC)时，航迹角很小，有cosθ≈1，于是有

(13)

利用准平衡滑翔条件：

(14)

可得

(15)

代入(13)式得

(16)

假设再入过程中升阻比已知且为常数, 则以常值倾侧角积分(16)式得

(17)

利用(17)式和终端能量及航程约束可求得常值倾侧角幅值:

(18)

以上求取倾侧角的解析方法是基于再入过程满足准平衡滑翔条件推导得到的，然而实际飞行可能不满足准平衡滑翔条件，于是该方法的准确性不能得到保证。为了保证该解析解的精度，同时抑制再入过程中的轨迹振荡问题，本文在倾侧角指令中反馈高度变化率，使升力更快地平衡重力，从而抑制高度振荡问题，使轨迹满足准平衡滑翔条件[4]，即

(19)

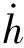
(20)

由于滑翔初始段轨迹振荡幅值较大，此时倾侧角应侧重于振荡的抑制；而滑翔末段振荡较轻，此时倾侧角应侧重于航程的校正。故反馈系数k可取为能量的函数：

(21)

式中：k0=30；kf=10；e0为滑翔段初始能量值；et=0.99ef.

以上倾侧角解析解的精确程度不仅取决于轨迹是否满足准平衡滑翔条件，也与常值升阻比假设有关。为此，每个制导周期内需实时更新方程(18)式中的升阻比信息。由于攻角尚未确定，可按上一周期的攻角计算升阻比。随着飞行器距离目标点越来越近，剩余航程越来越小，升阻比的变化范围更小，更加接近于常值，倾侧角解析解的精度会不断提高。

2.2 攻角解析解

以终端能量为积分终止条件，根据倾侧角解析解可保证终端航程约束和能量约束。传统预测校正算法一般将终端高度和速度约束转化为终端能量约束，但保证终端能量并不能严格约束终端高度。

进一步考虑准平衡滑翔条件(14)式，再入过程中无量纲地心距r≈1，于是有

Lcosσ+(v2-1)=0.

(22)

观察(22)式，对于给定终端速度，由于升力加速度L随高度的增大而减小，此时的倾侧角应减小才能满足准平衡滑翔条件。即终端高度约束对应了一个倾侧角。也就是说根据终端航程约束可确定一个倾侧角，根据终端高度约束也可确定一个倾侧角。当航程约束与高度约束不匹配时，很难通过一个倾侧角指令同时满足终端航程约束和高度约束。然而，(22)式中还隐含另一个控制量攻角，可利用攻角满足终端高度约束。

首先，由(3)式和(11)式可求得航程对高度的微分：

(23)

(24)

于是可求得满足高度与航程约束的期望航迹角：

(25)

(25)式得到的是航迹角期望值，与实际值并不相符，需要设计控制律对其跟踪：

(26)

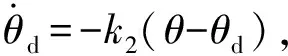
于是得到了期望的航迹角变化率，然后利用航迹角动力学方程：

(27)

求出升力系数：

(28)

进而根据升力系数反插值求出攻角指令。

以上攻角解析解的精确程度主要取决于常值航迹角假设是否合理。滑翔初始段航迹角变化较大，利用上述方法求得的攻角指令可能偏差很大，甚至不在攻角的实际可取范围内。由于滑翔初始段不需考虑终端高度，正常飞行即可，同时考虑到初始段的热保护要求和后续的航程要求，采用分段函数形式的攻角方案：

(29)

式中：αm为一个较大的攻角；αL/D为最大升阻比攻角；vm和vL/D为预先设定的速度值。

当满足e>ep时(ep为预先设定的能量值)，攻角指令由方案(29)式切换至由(28)式得到的解析解：

(30)

滑翔后段基本满足准平衡滑翔条件，轨迹比较平直，常值航迹角假设合理，利用攻角解析解可保证终端高度约束。

此外，为了减小攻角指令由攻角方案切换至解析指令时的突变并保证终端航迹角跟踪精度，将误差系数γ设计为

式中：γ0=1；γf=0.75；ep=0.9ef；et=0.99ef.

2.3 过程约束管理

过程约束控制一直是预测校正制导的难点之一。传统方法一般利用准平衡滑翔条件将过程约束转化为倾侧角走廊，然而，再入过程中准平衡滑翔条件不一定严格成立，并且实际飞行中的大气环境扰动和飞行器参数不确定性也使得这种倾侧角走廊的可靠性难以保证。文献[4]基于时标分离原则提出了一种在线预测约束管理方法。在此基础上，本文设计了一种基于航迹角指令的在线约束控制方法。

以动压约束为例，当实际动压接近最大动压值即q≥μqmax时，其中μ为接近于1但小于1的常数，可取为0.98，于是设计反馈控制律：

(31)

式中：kq=0.1为动压反馈系数。于是实际动压可跟踪一个给定的期望值，该期望值比最大动压略小，从而满足动压约束。然后对(8)式求微分得

(32)

(33)

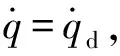
(34)

类似地，可求得满足热流约束和过载约束的航迹角指令值：

(35)

(36)

(37)

当实际飞行中的过程约束接近或超过最大值时，根据(37)式求出航迹角指令θc，然后利用(30)式求出相应的攻角指令以满足过程约束。此过程中产生的终端误差可在后续的制导周期中得到弥补，从而不影响最终精度。

实际仿真中发现，上述获得的攻角指令可能存在抖振和不连续问题。为使攻角指令平滑易于跟踪，将指令进行1阶低通滤波：

α(i)=χαd(i)+(1-χ)α(i-1)，

(38)

式中：0<χ<1为滤波系数，可取为0.1；α(i)为当前的实际攻角指令；α(i-1)为上一时刻的实际攻角指令；αd(i)为当前由(30)式计算得到的攻角指令。

2.4 侧向制导

对于侧向制导，本文采用经典的航向角走廊方法确定倾侧角符号。设ψLOS为飞行器当前点到目标点的视线角，其计算公式为

(39)

则当前航向角误差为ψ-ψLOS. 当航向角误差超过预设的误差走廊时，改变倾侧角符号使其重新回到走廊内，当航向角误差未超过误差走廊时，保持倾侧角符号不变，即

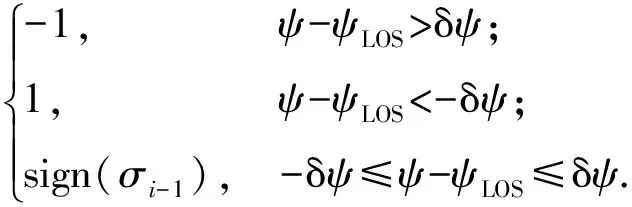
(40)

式中：σi-1为上一时刻的倾侧角；σi为当前时刻的倾侧角；δψ为航向角误差门限。

3 仿真分析

本文以通用航空器CAV-H为仿真对象[26]。该飞行器质量907 kg，参考面积0.483 9 m2. 攻角方案参数αm=20°，αL/D=10°，vm=6 500 m/s，vL/D=5 000 m/s，误差门限δψ=15°，过程约束设置[27]为

(41)

再入任务初始和终端状态设置如表1所示。

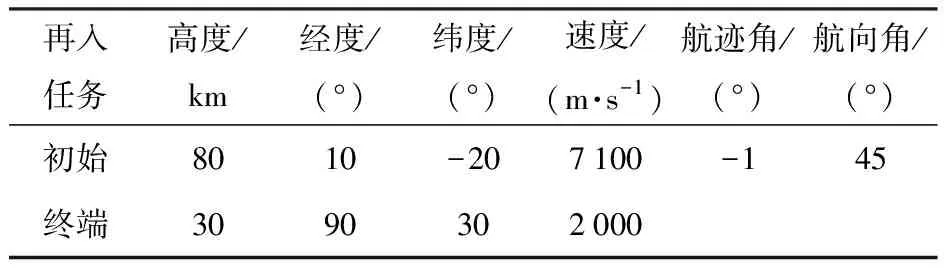
表1 再入任务初始和终端状态

仿真环境为Windows10操作系统，仿真计算机CPU主频3.2 GHz，内存4 GB，制导周期为10-4无量纲能量。

3.1 标准条件下制导方法仿真

为了验证所提出解析制导方法(简称方法1)的有效性与优越性，本节将其与文献[6]中常值倾侧角数值预测校正制导方法(简称方法2)在标准条件下以相同仿真环境和制导周期作对比。方法2以终端能量为约束，不能严格保证终端高度，且未考虑轨迹振荡问题。仿真结果如表2和图1所示。

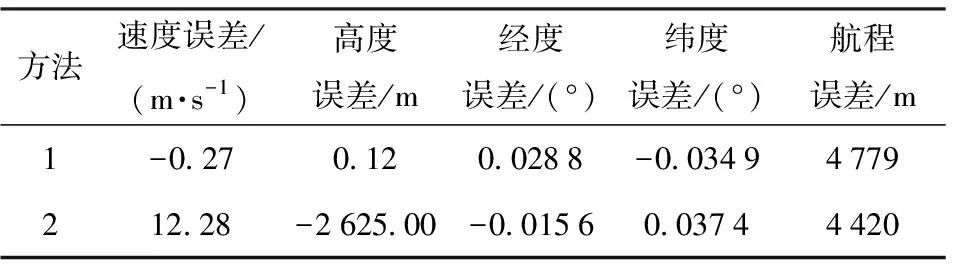
表2 终端误差

表2为两种方法的终端误差。两种方法的航程误差均较小，具有一定精度。方法2的终端高度误差较大，这是因为该方法仅以终端能量为约束，不能严格约束终端高度。而本文所提出的方法根据终端高度约束得到攻角指令，终端速度、高度误差均很小，满足终端高度约束。图1为标准条件下的高度- 速度曲线。相比方法2，方法1中由于添加了高度变化率反馈，轨迹更加平滑，无明显振荡，基本满足准平衡滑翔条件，更加适用于高升阻比的高超声速滑翔飞行器。

图2为标准条件下的地面轨迹，图3、图4分别为标准条件下的倾侧角和攻角。方法1的倾侧角初始阶段变化较大，这是因为为了尽快满足准平衡滑翔条件，在控制指令中加入高度变化率反馈造成的。相比之下，方法2的倾侧角幅值近似为常值。方法2的攻角指令完全按照攻角方案给出。而方法1在滑翔末端为满足终端高度约束，根据航迹角指令设计攻角指令，使攻角逐渐增大以抬高终端高度满足终端高度约束。

图5～图7分别为标准条件下的各过程约束曲线。两种方法均可满足各过程约束，相比方法2，方法1的过程约束变化更加平滑，无周期性振荡现象且峰值较小，更易于飞行器承受。

图8为方法1在标准条件下的升阻比和航迹角曲线。由图8可知，再入过程中，升阻比变化平缓且变化范围较小，可近似于常值；滑翔段航迹角变化不大，也可认为是常值。随着飞行器距离目标点越来越近，剩余航程越来越小，升阻比和航迹角的变化范围更小，更接近于常值，解析解的精度会不断提高。

此外，在相同的仿真环境和制导周期下，方法1的计算时间比方法2的计算时间小两个数量级以上，这显示出解析制导相比数值预测校正制导在计算效率上的优越性。

3.2 扰动条件下制导方法仿真

为了验证所提出的方法在扰动条件下的精度和鲁棒性，进行200次蒙特卡洛仿真。仿真中各初始状态偏差和参数偏差假设符合正态分布，其偏差限如表3所示。

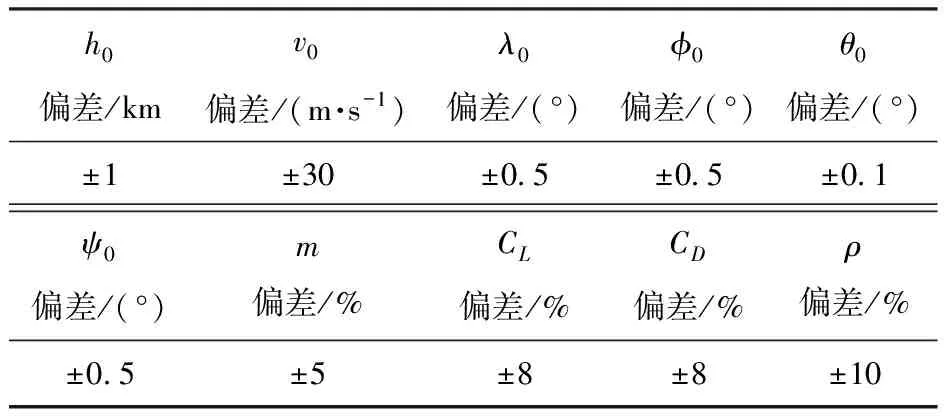
表3 参数偏差

图9为扰动条件下的高度- 速度曲线。由图9可见，扰动条件下的轨迹仍比较平滑，基本满足准平衡滑翔条件。轨迹末端分布较宽，这是调整终端高度造成的。图10为扰动条件下的终端高度- 速度误差散布。由图10可见，终端高度误差基本在200 m以内，速度误差在1 m/s以内，仍具有较高的精度。图11为扰动条件下的落点散布，可见落点基本散布在10 km以内，满足再入制导要求。

图12～图14分别为扰动条件下的各过程约束曲线。本文提出的方法在扰动条件下仍可满足各过程约束。特别是对于动压约束，利用本文所提出的在线约束控制方法，实际动压可严格约束在最大动压150 kPa以内。

4 结论

本文针对高超声速滑翔飞行器再入制导问题，提出了一种基于准平衡滑翔的解析制导方法。理论分析和仿真结果表明：

1)利用基于准平衡滑翔条件得到的近似解析关系求得的倾侧角指令和攻角指令可保证终端航程约束和高度约束，避免了传统预测校正制导中的数值计算，可为在线制导提供一定参考。

2)反馈高度变化率修正倾侧角指令可使轨迹平滑，并满足准平衡滑翔条件。

3)基于航迹角指令的在线约束控制方法可保证满足过程约束。

4)该方法在扰动条件下具有一定精度和鲁棒性。