一种声矢量阵最小方差无畸变方位估计算法

马伯乐， 朱世强， 孙贵青

(1.浙江大学 海洋学院， 浙江 舟山 316000； 2.92721部队， 浙江 舟山 316000;3.之江实验室， 浙江 杭州 310000)

0 引言

矢量水听器可以空间同步共点测量声压与振速信息，由于额外信息的存在，相比常规声压阵，声矢量阵具有更精确的方位估计能力，并可以有效克服左右舷模糊[1-2]。近年来国内外学者对于阵列方位估计开展了大量研究[3-17]，主要采用的方法包括：1)波束扫描类算法；2)子空间类算法；3)稀疏分解类算法。其中波束扫描算法无需信源个数的先验知识，稳健性较好，已成为目前最为实用的方位估计方法。

声矢量阵波束扫描的主流方法有：

1)将矢量阵各个接收阵元顺序排列构造成一个长阵列结构，直接套用相应的标量阵列波束形成算法[13]。这种处理很好地利用了单矢量水听器单边指向性优势，可以提高波达方位(DOA)估计的分辨力，并且可以抑制左右舷模糊[12]。但长阵列形式的处理法没有充分利用声压振速对各向同性噪声的抑制能力，因此其DOA估计能力改善有限。

2)基于联合信息处理的矢量阵DOA估计[9,13]，该处理方法可以很好地提高信噪比，并保留矢量水听器单边指向能力。

本文首先分析长阵列结构AVAMVDR算法性能，介绍了两种协方差矩阵构造方法，并在此基础上提出一种改进的AVAMVDR(IAVAMVDR)算法，通过仿真与实测数据证明了本文算法的有效性。

1 AVAMVDR算法

以水平均匀线阵情况为例：接收信号为远场平面波，不同方位信号间独立；环境噪声为高斯分布的水平各向同性噪声场；矢量传感器为二维矢量水听器。阵列由N个矢量传感器构成，阵元间距为d；设有k个目标，则阵列接收信号模型为

x(t)=A(θ)·S(t)+N(t)，

(1)

式中：A(θ)为阵列流形，

A(θ)=[αp(θ1)⊗D(θ1) …αp(θk)⊗D(θk)]，

(2)

θ为目标角度，αp(θ)为声压阵的导向矢量，对于第i个目标，有

(3)

θi为第i个目标角度，λ为信号的波长，D(θ)为单个矢量水听器的方向矢量，对于第i个目标，其值为

D(θi)=[1,cosθi,sinθi]T；

(4)

S(t)为目标信号矢量；N(t)为噪声矢量。

传统AVAMVDR算法空间功率谱表达式为

(5)

式中：C(θ)为搜索方向矢量；R为信号协方差矩阵，

R=E[x(t)·xH(t)]=A(θ)·Λs·AH(θ)+Λn，

(6)

(7)

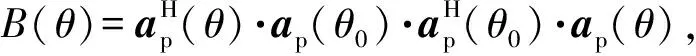
(8)

式中：λmax为信号对应的最大特征值；Us、Unj分别为信号子空间与噪声子空间。传统AVAMVDR算法是通过大特征值倒数，减少信号子空间影响，并利用导向矢量与噪声子空间的正交性来实现目标方位的估计，因此随着信号对应特征值的变大，最后的估计效果会趋近多重信号分类(MUSIC)算法[10]。根据上述分析，本文将从减少信号子空间影响和保留方向因子两个方面，提高AVAMVDR算法方位估计性能。

2 协方差矩阵构造方法

充分利用声压- 振速抗各向同性噪声能力[9]与解析振速结构，本节给出协方差矩阵构造方法。首先，得到一个解析振速为

Va=Vx+j·Vy，

(9)

式中：Vx、Vy分别为振速x通道与y通道信号。结合声压通道得到两种协方差矩阵为

R1=E[Va·PH]，

(10)

(11)

P为声矢量阵的声压部分。由于声压振速抗各向同性噪声能力[9]，(10)式、(11)式不含噪声项。依据文献[14，18]中的原理，将(10)式与(11)式相乘，可得

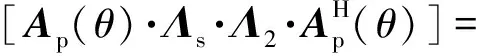
(12)

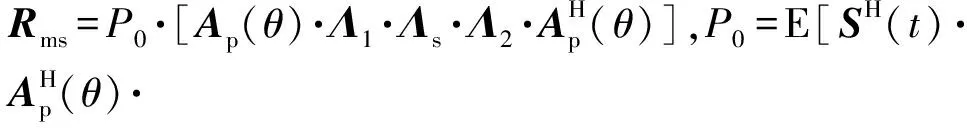
Vr=cosθ·Vx+sinθ·Vy，

(13)

得到协方差矩阵为

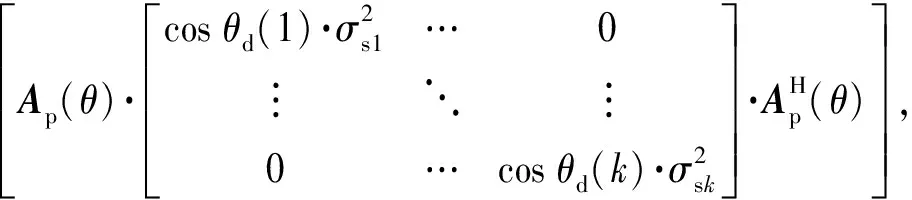
(14)

式中：θd(i)=θ-θ(i)为导向角度与第i个目标方位角之差，i=1,…,k. 将Rm对角线元素相加并开方得P0，并与Rrm做如下运算：

(15)

同理，根据文献[14，18]相关定理，可得

(16)

Y(t)=P+cosθ·Vx+sinθ·Vy，

(17)

进一步得到一个含噪声的类声矢量阵协方差矩阵：

(18)

3 IAVAMVDR算法性能分析

利用第2节类声矢量阵协方差矩阵，可得到一种AVAMVDR算法的空间功率谱：

(19)

以单目标为例，(19)式的分母可表达为

(20)

第1节指出，为提高角度分辨能力，必须尽可能减少信号子空间影响，为此进一步给出IAVAMVDR算法的空间功率谱为

(21)

以单目标为例，(21)式分母为

(22)

(23)

(24)

式中：AIAVAMVDR(θd)、AAVAMVDR(θd)分别为IAVAMVDR算法与传统AVAMVDR算法的方向因子；SNR′、SNR表达式为

(25)

(26)

由归一化空间功率谱表达式可见，信噪比与阵元个数是影响传统AVAMVDR算法角度分辨力的主要参数,利用半功率波束宽度(HPBW)指标进行比较。图1给出了目标方位30°、信噪比0 dB、阵元个数2～10情况下IAVAMVDR算法与传统AVAMVDR算法的HPBW，图2为信噪比-8～10 dB情况下6元阵HPBW比较图。从图1和图2可见，随着阵元个数和信噪比增加，IAVAMVDR算法与传统AVAMVDR算法的HPBW逐渐减小，但IAVAMVDR算法的HPBW均小于传统AVAMVDR算法。由此可见，相比于声矢量阵常规处理方法，本文算法具有更好的角度分辨能力。

4 仿真分析

仿真1对传统AVAMVDR算法与本文IAVAMVDR算法的空间功率谱进行比较。仿真条件如下：单目标入射角度60°；双目标入射角度为60°和80°；采样快拍1 000；中心频率1.5 kHz;采样频率10 kHz;6元矢量均匀线阵；阵元间距半波长；信噪比0 dB. 图3、图4给出了相应仿真结果。图3和图4中，由于方向因子的调制作用，传统AVAMVDR算法与IAVAMVDR算法在模糊方位处均形成较好抑制，单目标情况下，抑制度分别为10.88 dB与11.31 dB. 由于本文算法信号部分对应信号子空间得到较大抑制，IAVAMVDR算法具有更窄的主瓣与更低的旁瓣，相比于传统AVAMVDR算法旁瓣最多低7.77 dB. 双目标情况下，两种算法都能正确识别双目标，但IAVAMVDR算法具有更好的角度分辨能力，同时旁瓣最多相差4.83 dB.

仿真2从单目标估计精度、双目标分辨概率两个方面对IAVAMVDR算法与传统AVAMVDR算法的方位估计能力进行比较。仿真条件如下：快拍数1 000；信噪比变化范围-8～10 dB；100次蒙特卡洛实验；其余仿真条件与仿真1一致。图5给出了单目标情况下均方根误差图。从图5中可见，随着信噪比增加，两种算法的均方根误差都呈下降趋势，但在低信噪比情况下，IAVAMVDR算法的估计精度优于传统AVAMVDR算法。图6给出了双目标情况下两种算法的分辨概率。从图6中可见，随着信噪比增加，两种算法的识别概率逐渐上升，IAVAMVDR算法在低信噪比情况下，识别概率要大于传统AVAMVDR算法，特别在-5 dB以后IAVAMVDR算法可以100%识别双目标，但传统AVAMVDR算法需要-3 dB以后才可以准确识别。由此可见本文算法具有较佳的角度分辨能力。

5 实测数据验证

本文给出某次湖试的实测数据结果。传感器为4个同振式矢量水听器组成的均匀线阵；目标信号为中心频率为3.15 kHz的脉冲信号；采样频率96 kHz，数据长度5 s；目标大致方位87°左右。图7给出了传统AVAMVDR算法与IAVAMVDR算法的空间功率谱图。由图7可见，传统AVAMVDR算法与IAVAMVDR算法在模糊角度处形成抑制，都保留了单边指向性。同时IAVAMVDR算法的HPBW窄于传统AVAMVDR算法 7°，并且旁瓣最多相差6 dB. 由此可见，本文的IAVAMVDR算法性能优于传统AVAMVDR算法处理。

6 结论

本文在传统AVAMVDR算法性能分析基础上利用解析振速结构与矢量水听器抑制各向同性噪声能力，给出一种协方差矩阵构造方法，在提高信噪比同时，保留了方向因子；通过声压与电子旋转振速组合得到一种含有噪声的协方差矩阵；将两种矩阵相加，实现AVAMVDR目标方位估计。通过仿真与实测数据验证，得到以下结论：

1)由于矩阵相加，信号对应特征值变大，有效抑制了信号子空间影响，使得主瓣更窄、旁瓣更低。

2)由于方向因子作用的存在，本文算法具有一定的抗空间模糊能力，双目标情况下，相比于传统处理方法旁瓣抑制能力更强。