多平台主动与被动传感器协同跟踪的长时调度方法

乔成林， 单甘霖， 段修生,2， 郭峰

(1.陆军工程大学石家庄校区 电子与光学工程系, 河北 石家庄 050003; 2.石家庄铁道大学 机械工程学院, 河北 石家庄 050043;3.北京航天飞行控制中心, 北京 100094)

0 引言

网络化战争中，战场中分布大量多种型号的传感器，如何管理这些传感器资源以满足作战任务需求，具有重要的意义。目前，以主动、被动传感器协同跟踪为代表的调度方法正逐渐受到学者的重视，通过合理地调度主动、被动传感器可以满足任务需求、降低系统辐射。文献[1]研究了单平台主动、被动传感器辐射控制方法，当满足精度需求时调度被动传感器，否则调度主动传感器。考虑杂波环境，文献[2]提出一种机载雷达辅助无源传感器的机动目标跟踪方法。进一步，吴巍等[3]研究了多平台主动、被动传感器调度方法，并提出一种时间- 空间辐射控制方法，即时间上优先选择被动传感器，若不能满足任务需求，则在空间上选择威胁度最小的主动传感器，从而降低系统辐射。实际上，不同主动传感器的使用代价是不同的，文献[4]通过量化主动传感器辐射代价，构建跟踪任务需求下传感器调度模型，实现了对目标的协同跟踪。然而，由于未考虑切换代价，系统容易产生频繁切换，不利于实际应用。

此外，依据决策步长，传感器调度方法可分为短时调度和长时调度。短时调度以当前单步收益为决策准则，因此文献[1-4]的调度方法均可认为是短时调度。相对于短时调度方法，长时调度以未来一段时域内的收益为决策准则，其性能往往更优越。文献[5]研究了多被动传感器长时任务规划问题，采用基于蒙特卡洛Rollout采样的Q值估计方法实现对目标的协同跟踪。文献[6]将空间态势感知中多传感器长时调度问题转化为多Agent马尔可夫决策过程，给出基于随机仿真的随机优化技术，实现了对多个动态目标的协同监测。文献[7]针对声纳传感器长时调度问题，提出一种连续概率状态算法，实现了对多个水下目标的持续跟踪。然而，长时调度方法的计算量随决策步长增加呈指数爆炸增长[8]，如何降低搜索空间、提高算法实时性显得尤为重要。

针对上述问题，本文提出一种多平台主动与被动传感器协同跟踪的长时调度方法。首先，构建基于部分可观马尔可夫决策过程(POMDP)的长时调度模型；然后，考虑跟踪任务需求，引入传感器辐射代价和切换代价，建立长时目标优化函数；最后，提出改进的维特比算法(VA)，求解最优调度序列。仿真结果验证了所提搜索算法和调度方法的有效性。

1 多平台主动与被动传感器调度模型

在多平台主被动传感器系统中，一方面主动传感器通过向外辐射电磁波获得目标位置信息，但其辐射代价较高；另一方面被动传感器无需辐射电磁波就能获知目标的角度信息，但信息的缺维会导致跟踪精度发散。为此，考虑跟踪任务需求和主被动传感器特性，依据POMDP理论[9]，建立基于POMDP的传感器长时调度模型，以满足跟踪任务需求、降低系统辐射代价。

1.1 平台调度动作及传感器调度动作

(1)

1.2 状态空间及状态转移律

系统状态空间Sk由目标运动状态Xk、平台调度动作ak、传感器调度动作gk及目标运动模型mk组成，则k时刻：

(2)

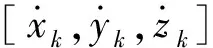
目标状态按照其状态转移律转移到下一时刻，即

Xk+1=f(Xk,mk,vk)，

(3)

式中：vk为零均值高斯过程噪声，其协方差矩阵为Qmk.

进一步，机动目标状态转移律可由目标运动模型mk获得，则其对应的状态转移律可表示为Fmk.

1.3 观测空间及观测律

目标观测律取决于传感器观测模型，即

(4)

式中：wk为零均值高斯观测噪声；rk+1表示k+1时刻平台与目标的距离；Th为相应传感器的作用范围，当目标处于传感器作用范围内时，传感器能获得目标量测信息，否则不能。

若调度平台上主动传感器(如雷达)，则

Zk+1=h(Xk+1,ak,gk,wk)=[rk+1,θk+1,φk+1]Τ+wk，

(5)

式中：θk+1和φk+1分别表示方位角和俯仰角。

相似地，若调度平台上被动传感器(如红外传感器)，则

Zk+1=h(Xk+1,ak,gk,wk)=[θk+1,φk+1]Τ+wk.

(6)

1.4 信念状态

考虑到目标跟踪系统中，状态不能被完全观测，引入目标信念状态bk，以实现对目标运动状态的持续更新[5]，则定义信念状态为

bk=p(Xk|X0,p0,Z1,…,Zk,a0,…,ak-1,g0,…,gk-1)，

(7)

式中：X0和p0为目标初始状态及其分布概率。

1.5 目标优化函数

不同的应用场景，性能衡量指标往往不同。为此，结合战场应用实际，本文引入3种性能指标，即目标跟踪精度、传感器辐射代价和切换代价，分别表征系统的目标跟踪性能、生存性能和稳定性能：

1)目标跟踪性能ρ(bk,ak,gk)。为了满足跟踪任务需求，需要协同调度各平台各类型传感器。对于杂波条件下的机动目标，由于当前时刻不能准确地获知未来时刻的量测，较难准确地获知其跟踪精度。为此，引入后验克拉美- 罗下界(PCRLB)指标，以表征其跟踪性能。

2)传感器辐射代价E(ak,gk)。考虑到主被动传感器辐射电磁波的差异性，主动传感器的辐射代价要大于被动传感器。结合文献[10]，可假设被动传感器的辐射代价为0，此外，由文献[11]可知，不同主动传感器的辐射代价也不同。

3)切换代价γ(ak-1,ak,gk-1,gk)。在传感器调度中，为了获得最优调度性能，系统常面临频繁切换问题，从而极大影响了系统稳定性和可操作性。为此，结合实际，引入切换代价[12]。显然，不同平台间的切换代价要远大于同一平台内传感器的切换代价，下文分别简称为平台切换代价和传感器切换代价。

因此，定义短时代价函数为

(8)

式中：α表示平衡系数；en、cp和cs分别表示传感器辐射代价、平台切换代价和传感器切换代价；δ(x,y)为指示函数，x=y时取值为0，否则为1.

相比于短时代价函数，长时代价函数能进一步提高系统性能。考虑跟踪精度需求，构建长时代价函数的目标优化函数，即

(9)

式中：Ak:k+H-1={ak,gk,…,ak+H-1,gk+H-1}，H为决策时长；ρd为任务需求对应的精度阈值。

传感器长时调度包含两种模式：开环调度和开环反馈调度，本文调度属于后者，其调度流程如图1所示。任意k时刻，调度中心根据目标优化函数获得最优调度序列Ak:k+H-1，而后选择第1个调度动作(ak,gk)实现目标信念状态的更新。由于加入反馈环节，开环反馈调度的性能要优于开环调度，但其计算量也更高。

2 问题求解

2.1基于交互式多模型概率数据关联算法的信念状态更新

为有效估计杂波环境下机动目标状态、更新其信念状态，引入交互式多模型概率数据关联(IMMPDA)算法[13]，其执行步骤如下：

1)相互作用。依据先验信息，计算混合概率：

(10)

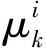
进一步，计算模型j的混合初始状态及其协方差矩阵：

(11)

2)滤波。

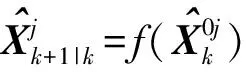
(12)

式中：ZXk+1表示实际观测值；l为最大有效区域对应的模型；ε为波门参数；|·|为求行列式。

若ZXk+1满足(12)式，则将其作为候选回波；否则舍弃该观测。

③ 估计模型j状态。假设共有nk+1个候选回波，则

(13)

(14)

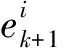
3) 更新模型概率。似然函数是nk+1个新息的联合概率密度函数，即

(15)

式中：PD表示检测概率；PG表示门概率；nz为观测向量的维数；cnz为相应超球面体积。

进一步，更新模型概率，即

(16)

式中：πj为列向量；μk和c分别为模型概率和归一化因子。

4) 目标信念状态更新。估计目标状态及其协方差矩阵

k+1)k+1)T]，

(17)

更新k+1时刻目标信念状态，即

bk+1～N(Xk+1;

(18)

2.2 机动目标长时精度预测

考虑到当前时刻无法获知未来时刻目标的量测信息，结合PCRLB理论，依据当前先验信息，计算目标的状态估计下界，并以此作为目标的预测精度，从而合理地调度传感器以满足跟踪精度需求。

根据PCRLB理论，则存在

E(

(19)

式中：Jk为Fisher信息矩阵。

进一步，目标状态转移先验概率密度函数为

(20)

式中：mk+1表示k+1时刻目标的运动模型。

Fisher信息矩阵递推公式为

(21)

显然，在k时刻无法获知目标的运动模型。为此，依据k时刻的模型概率，以当前最大概率对应的模型作为目标预测模型[15]，则

(22)

因此，机动目标跟踪精度预测流程为

1) 根据k时刻信念状态bk，获得目标状态估计k、协方差Pk及模型概率μk.

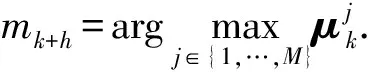
3)计算p(Xk+h|Xk)。再依据(21)式计算k+h时刻Fisher信息矩阵Jk+h.

2.3 改进VA

考虑(9)式的优化模型，其共有(2N)H种传感器组合。当N和H较大时，其计算量将是巨大的，难以满足实时性要求。动态规划具有广泛的应用范围，尤其适用于节点状态及路径代价已知的优化问题。然而，本文优化模型中各节点的状态及其路径代价取决于传感器序列，不同传感器序列，节点的状态及路径代价是不同的[16]。为此，提出改进的VA以满足本文应用。

假设以传感器节点状态和决策步长分别代替VA的节点状态和路径长度。此时，VA的节点状态不再是一个标量，而是包含了目标跟踪误差和使用代价的向量。相应地，路径代价由前后传感器节点实时计算获得。为了进一步降低算法复杂度，考虑到被动传感器的辐射代价为0，结合贪婪策略，当平台被动传感器能满足要求时优先调度被动传感器。

以N=3为例，改进VA搜索流程图如图2所示，其具体的执行步骤如下：

1) 初始化，根据目标信念状态bk获得k时刻目标状态Xk及其协方差Pk.

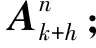
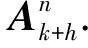
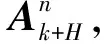
利用上述步骤能够快速求解最优传感器调度序列，若不存在最优解，则采用以下原则：

2)若在执行步骤2时搜索不成功，即下一时刻所有传感器均不能满足跟踪精度需求，则选择跟踪误差最小的传感器作为最优调度序列，以快速满足精度需求。

2.4 复杂度分析

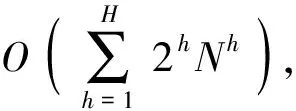
3 仿真实验及结果分析

3.1 仿真参数设置

考虑N=4个平台在杂波环境下协同跟踪一个机动目标，用M=3个模型来描述目标运动，模型1为匀速直线，模型2为左转弯，模型3为右转弯。假设目标初始位置和速度分别为(15 km,4 km,5 km)和(-280 m/s,-260 m/s,0 m/s)。进一步，假设采样间隔τ=1 s，仿真时长为100τ. 在26～50τ时间内目标以角速度5°向右转，在51～74τ时间内向左转，其余时间做匀速运动。各模型初始概率为[0.8,0.1,0.1]，不同模型之间的切换概率为0.025. 此外，假定杂波服从泊松分布，主动和被动传感器的虚假量测密度分别为3×10-9个/(m·mrad2)和1×10-3个/mrad2，检测概率为1，波门参数为4，门概率为0.999 7.

各平台分布在Oxy平面内，均距离坐标原点5 km，相互间隔90°. 平台上主动和被动传感器探测范围分别为60 km和10 km. 主动传感器的斜距离标准差分别为100 m、50 m、50 m和20 m，方位角标准差分别为10 mrad、5 mrad、5 mrad和2 mrad，对应的俯仰角标准差与方位角一致。各平台被动传感器性能一致，其方位角和俯仰角标准差均为5 mrad. 各平台主动传感器辐射代价设为[1,2,2,3]。仿真实验中，所有仿真结果均为500次独立蒙特卡洛仿真取平均值。

3.2 仿真结果分析

3.2.1 不考虑切换代价

图3为不同精度阈值和决策步长下的累积辐射代价。由图3可知，随着跟踪精度阈值的提高，可以调度更多的被动传感器满足需求，因此其累积辐射代价更小。相同跟踪精度阈值下，随着决策步长的增加，其累积辐射代价更小，即系统能够获得更优的调度序列。此外，累积辐射代价随着决策步长的增加，其下降幅度逐渐变小，而且决策步长越大其计算复杂度越高。因此在实际应用中，需要权衡各个要素，选择合适的决策步长。

以跟踪精度阈值ρd=50 m为例，表1给出了不同算法不同决策步长的搜索性能对比。表1中ES为穷举搜索，UCS为标准统一代价搜索，表中UCS算法和改进VA的百分比为其相应的节点打开数与ES算法节点打开数的比值。图4为UCS算法和改进VA的节点打开百分比。由表1和图4可知，UCS算法以代价为顺序进行搜索，有效提高了搜索效率，但其节点打开数依然较大且需要较大的存储空间。相比于UCS算法，本文提出的改进VA能够显著地减少节点打开数、降低存储空间。图5为不同决策步长的累积辐射代价。图5中，最优值对应的曲线是由UCS算法获得(之后不再赘述)，随着决策步长增大，系统能够搜索到更优的调度序列，使得其累积辐射代价更低，进而验证了长时调度模型的必要性。此外，由于改进VA采用贪婪策略降低搜索空间，当决策步长H>1时，其只能获得次优解，对应的累积辐射代价要略高于最优值。结合图3可知，随着决策步长增加，累积辐射代价下降幅度变小。因此，考虑到算法复杂度，之后的仿真实验以H=4为例。

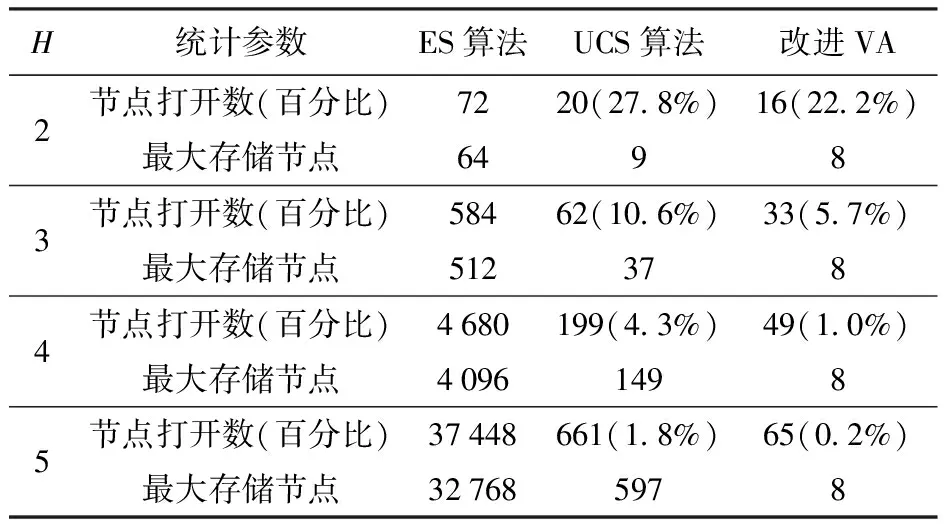
表1 算法搜索性能对比

为了验证本文调度方法的有效性，引入随机调度方法(RSM)、最近邻调度方法(CSM)以及短时调度方法(MSM)进行对比。以ρd=50 m为例，图6为不同调度方法下的目标均方根误差(RMSE)对比。由图6可见，RSM和CSM不能依据跟踪精度阈值，自适应地调度传感器满足任务需求。而MSM和本文方法能够根据阈值要求，自适应地调度传感器以满足任务需求。此外，由于目标机动，在模型切换阶段，其RMSE不能满足任务需求，符合实际情形。图7为不同时间下的累积辐射代价。由图7可知，在整个时间范围内，RSM和CSM的累积辐射代价总体较高。本文方法(H=4)要优于MSM(H=1)。同时，考虑到本文方法采用改进VA，因此其累积辐射代价要略高于最优值。

图8为本文方法下的平台及传感器调度序列。结合图6可知，初始阶段目标较远且跟踪误差较大，为了满足跟踪精度需求，本文方法频繁调度主动传感器以满足精度需求。随着目标靠近平台，系统频繁地调度被动传感器以降低辐射代价，从而解释了图7中在中间阶段MSM和本文方法累积辐射代价几乎不变的原因。当目标再次远离平台时，系统会再次频繁地调度主动传感器以满足精度需求。因此，通过多平台主被动传感器协同跟踪，能够有效地满足跟踪任务需求、降低辐射代价。

3.2.2 考虑切换代价

由3.2.1节可知，不考虑切换代价时，虽然能够获得较低的辐射代价，但会频繁地发生切换、稳定性差。为此，引入切换代价，以权衡系统辐射代价和切换代价。取平台切换代价cp=1，传感器切换代价cs=0.5. 图9为不同平衡系数下累积辐射代价和累积切换代价的关系。由图9可知：平衡系数较小时，系统更注重稳定性，其累积切换代价较小；当平衡系数较大时，系统更注重生存性能，其累积辐射代价较低。不失一般性，取平衡系数为0.6，以权衡系统累积辐射代价和累积切换代价。

图10为不同方法下累积代价对比。由图10可知，RSM和CSM的累积总代价较高，本文方法以多步预测进行决策，要优于MSM以单步预测进行决策。同时，由于最优值能够搜索到更优的调度序列，其累积总代价更低。此外，引入切换代价，MSM、本文方法和最优值的切换代价相差无几，均能较好地平衡系统累积辐射代价和切换代价。

图11为考虑切换代价的平台及传感器调度序列。对比图8可知，当不考虑切换代价时，调度过程中频繁发生切换，其平台切换次数为30.6，同一平台内传感器切换次数为16.0. 当引入切换代价时，其平台切换次数仅为10.7，传感器切换次数为21.8. 引入平台切换代价后，调度过程中平台切换次数明显降低，更易实际实现。同时，由于平台切换代价大于传感器切换代价，为了降低系统辐射代价，根据目标函数优先调度同一平台内的主动或被动传感器。因此，在调度过程中，需要根据任务需求、综合各个因素，选择合适的平衡系数，以满足任务需求及其实际应用。

4 结论

本文建立了基于POMDP的传感器长时调度模型，引入目标跟踪精度、传感器辐射代价和切换代价，构建了长时代价函数；给出了基于IMMPDA算法的目标信念状态更新方法和基于PCRLB的机动目标长时精度预测方法，提出了改进VA搜索长时调度序列。得出以下结论：

1)所提改进VA以累积辐射代价略上升为代价，显著降低了搜索空间和存储空间。

2)不考虑切换代价时，与已有调度方法相比，所提长时调度方法能够获得更低的累积辐射代价，生存性能更优。

3)考虑切换代价时，所提长时调度方法累积代价更低，克服了传感器频繁切换、稳定性更好。