基于重要工况点的柴油机逐点模型标定∗
马 雷,王明露,陈 珂
(燕山大学车辆与能源学院,秦皇岛 066004)
前言
随着国五排放法规的全面实施,严格的排放法规要求柴油发动机在标定时需要更加复杂的电控系统和更多的控制装置,由于电控系统间复杂耦合关系导致了较长的标定周期和较高的标定成本[1]。传统的标定手段需要进行大量的发动机试验,其标定效率和精度很难满足当前日益复杂的标定系统。为此国内外都对发动机的电控系统标定进行了大量研究,提出了基于模型的标定方法。基于模型的标定是一种基于统计学理论的技术,主要包含:在发动机运转区间内进行工况点选取;通过发动机试验设计完成对各工况点下的试验点设计;对试验获取的发动机数据进行输入参数与响应参数间建立映射模型;完成对工况点最优参数选取,通过模型完成对发动机参数的优化[2-4]。文献[5]中通过分层抽样设计试验方案,使用Ordinary Kriging模型搭建燃烧参数与油耗间的映射关系,最终通过遗传算法完成对油耗响应的优化。该模型通常具有较高的拟合精度,但是由于采用分层抽样作为试验设计方案,因此无法灵活增减试验点。文献[6]中通过2阶响应模型搭建了燃烧参数与响应间的映射模型,最后使用遗传算法完成模型优化。该模型可通过较少的试验次数达到较高的模型精度,但该方法需要标定人员对发动机参数的运行边界有着详细的了解。因此该模型无法适用于某些全新的电控柴油发动机的标定工作。文献[7]中采用BP神经网络搭建响应,通过自适应网络模糊推理系统得到燃烧参数在全局空间的分布情况。该方法需要对较多的工况点进行试验,以提供足够的输入参数,因此该模型较其它模型所需试验次数较多。
本文中针对电控柴油机标定工作,以优化发动机燃油经济性和满足国五排放法规为约束,使用聚类分析完成工况点分类;结合发动机排放特征曲线筛选出重要工况点;通过对重点工况的优化从而降低了整体的油耗和排放水平。根据发动机基本运行边界参数,使用拉丁超立方试验设计完成工况点选取,从而减少试验量;通过2阶多项式混合径向基函数模型,搭建了发动机燃烧参数与响应参数间的响应模型;在进行模型误差分析时可灵活增减试验点,以提高模型精度。运用遗传算法完成各工况点寻优;结合多项式拟合完成初始MAP绘制;根据万有特性试验分析当前MAP下发动机油耗和排放较高区域进行重点优化,得到最优MAP。试验表明,逐点响应模型在满足国五标定的要求上,比人工标定大幅提高了标定效率,同时有效降低了整体油耗。
1 重要工况点选取
本文中以某型国五电控柴油机为研究对象,其基本参数见表1,使用HORIBA电力测功机、AVL颗粒采集仪、AVL缸压分析仪等设备完成发动机试验台架的搭建,见图1。发动机台架标定基于国家道路测试循环(NEDC),整个测试过程包括4个市区工况和1个郊区工况,共计11.01km,全部测试时间为1 180s。基于台架基本试验流程将测试循环中每秒所对应的车速与行驶阻力转换为代表发动机工况的发动机转速和平均有效压力[8]。
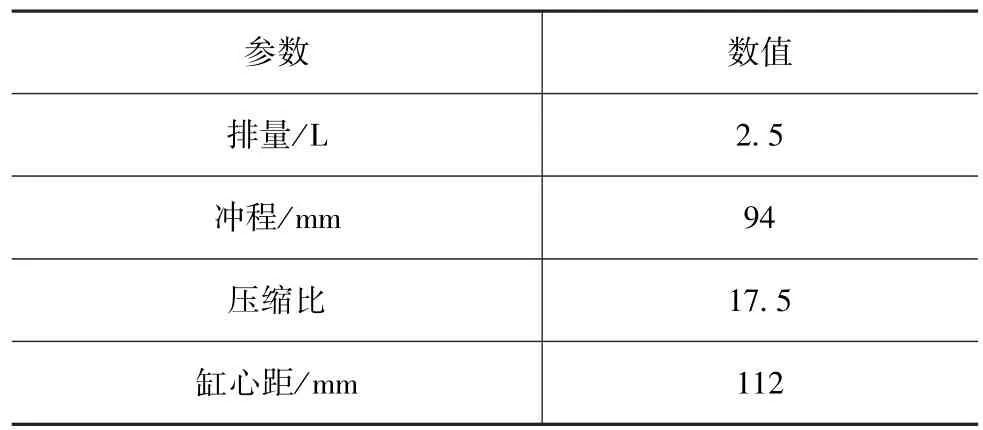
表1 发动机基本参数

图1 柴油机试验台架
1.1 车速与发动机转速的转换
汽车在行驶过程中的车速取决发动机输出转速、变速器和主减速器的配合,根据其间的关系,可得到NEDC循环下车速所对应的发动机转速关系为

式中:v为汽车行驶车速,km/h;ig为变速器速比;i0为主减速器减速比;r为车辆旋转半径,m。
1.2 整车行驶阻力与发动机平均有效压力转换
发动机的动力通过传动系统传递给车轮,主要包含了发动机摩擦阻力和地面行驶阻力。发动机摩擦阻力可通过发动机倒拖试验测得,根据测功机测量不同冷却液温度和转速下发动机摩擦转矩获得发动机摩擦转矩MAP,见表2。结合整车在NEDC循环中的冷却液温度变化曲线,可计算出发动机在NEDC循环下各点的摩擦转矩。
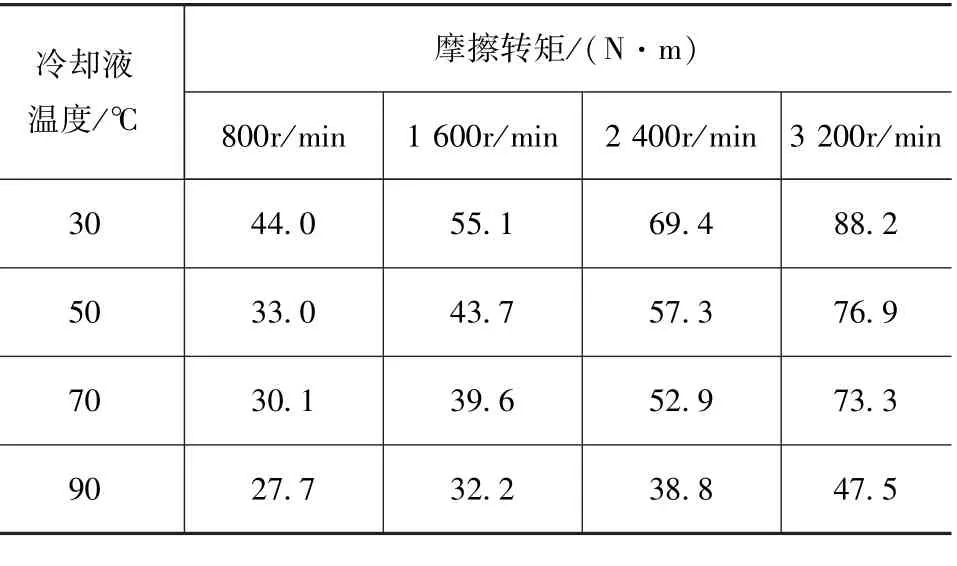
表2 发动机摩擦转矩MAP
根据交通部JT/T198—95《汽车技术等级评定标准》,汽车在道路上的行驶阻力可通过整车转鼓滑行试验测得。通过测量汽车在转鼓上滑行状态中所受的阻力,进而得到车辆行驶阻力。由此得到汽车行驶阻力与车速间二次拟合关系:

式中fi为多项式系数。
结合式(1)和式(2)可求得发动机每秒所对应的转矩输出,但是发动机标定过程中一般以平均有效压力作为发动机工况参数,因此需要将输出转矩转换为对应平均有效压力:

式中:BMEP为平均有效压力,MPa;T为输出转矩,N·m;Vs为发动机排放量,m3。
1.3 工况点分类
根据式(1)~式(3)可得到发动机所对应的1 180个工况点,工况点参数属于离线数据。选取目标为各工况点欧式距离(见式(4))最短,通过聚类分析完成NEDC 8工况点简化[9](由于低怠速状态下发动机的排放和油耗均可忽略不急,因此简化为7工况点)。
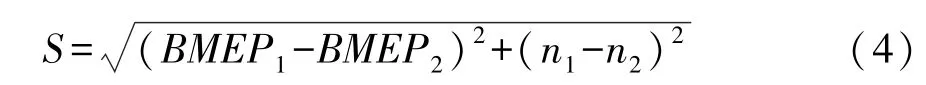
式中:S为欧式距离;ni为发动机转速,i=1,2。
其中发动机转速与平均有效压力存在较大的数量级差距,因此需要首先对工况点参数进行归一化处理,使其在相同范围内进行计算。
其分类过程包括:
(1)在工况点范围区域内随机产生7个初始工况点,作为初始聚类中心;
(2)依次计算各工况点到聚类中心的欧式距离,并根据最小距离重新对工况点进行分类;
(3)重新计算各聚类区域的聚类中心;
(4)若聚类中心发生变化,则重复第2步,若聚类中心未发生变化则聚类完成。
通过聚类分析可得到7个聚类区域,以及到各区域点欧式距离和最小的聚类中心。
1.4 基于发动机实际响应确定工况点
聚类分析所得到的聚类中心只能表明二维参数在坐标轴上的分布情况,无法保证所选出的工况点靠近油耗和排放的极值点,需要结合发动机实际排放参数,如图2和图3所示。
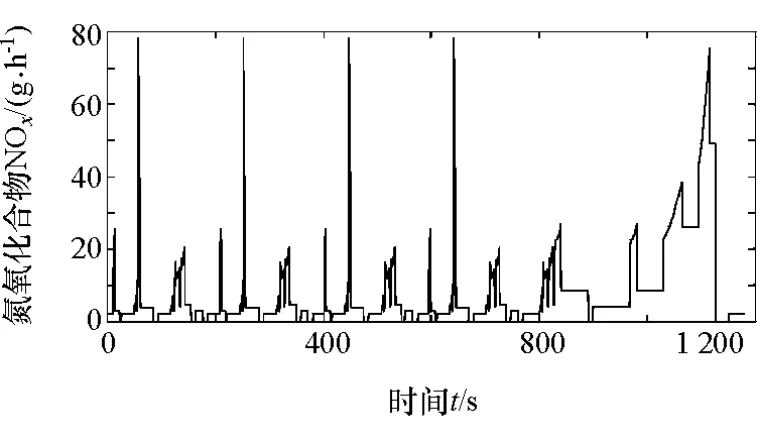
图2 氮氧化合物排放趋势图
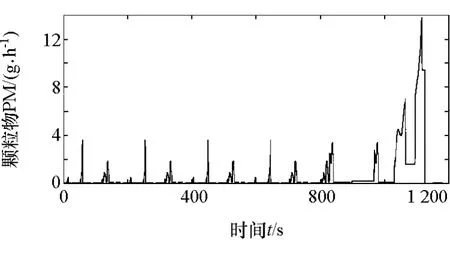
图3 颗粒物排放趋势图
选取各聚类区域内靠近聚类分析所得的聚类中心,且氮氧化合物和颗粒物排放值的均值较大点作为最终的工况点,见表3。
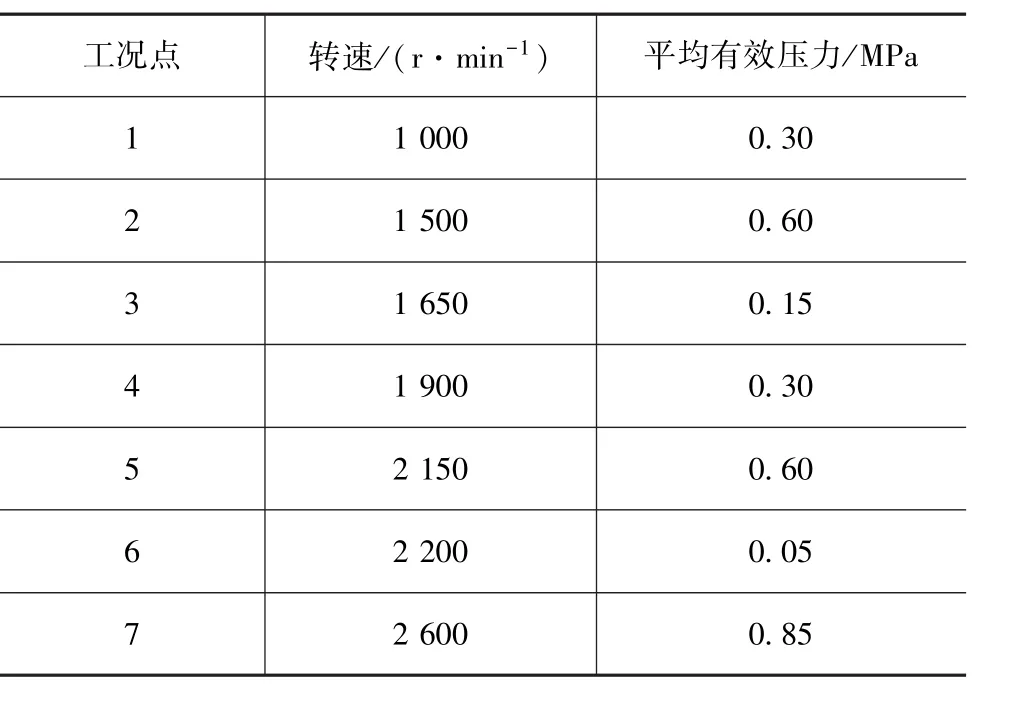
表3 发动机重要工况点
2 各工况试验点设计
试验各工况点下的燃烧参数包括轨压(Rail)、提前角(SOE)和循环空气量(Air)。若采用传统标定方法进行全因子试验,各工况点需要12×11×14,共1 848次试验。试验周期过长,需要新的试验方法完成各工况点的试验设计[10]。在Matlab中的MBC工具箱提供了3种不同的试验设计方法,包括经典设计法、空间填充法和优化设计法。在综合考虑模型精度和试验成本的基础上,本文中采用拉丁超立方抽样进行试验设计。
试验设计中为了缩小试验范围提高试验效率,需要通过外特性试验大致确定各工况点范围,表4为各工况点的燃烧参数的范围。
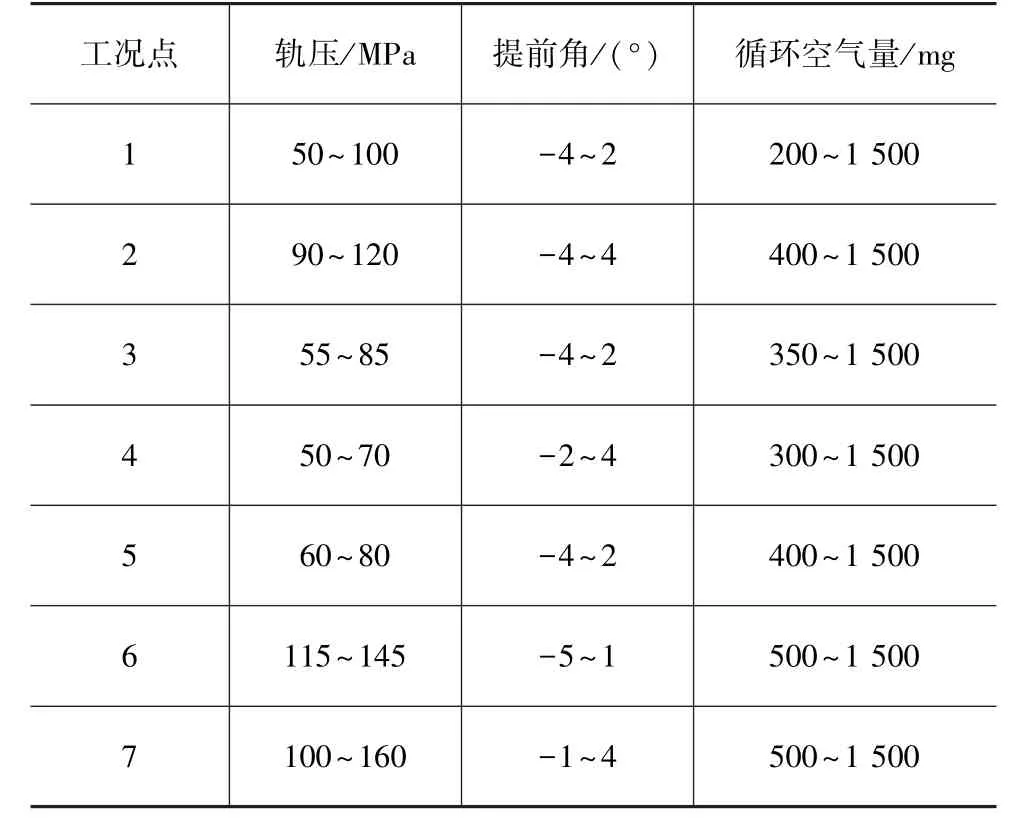
表4 各工况点参数边界
一般情况下试验区域内的试验点越多,则试验精度越高,但同时会增加试验成本,因此需要选择合适的试验点数。其中表5为不同点数下试验空间内的差异值和最小间距。
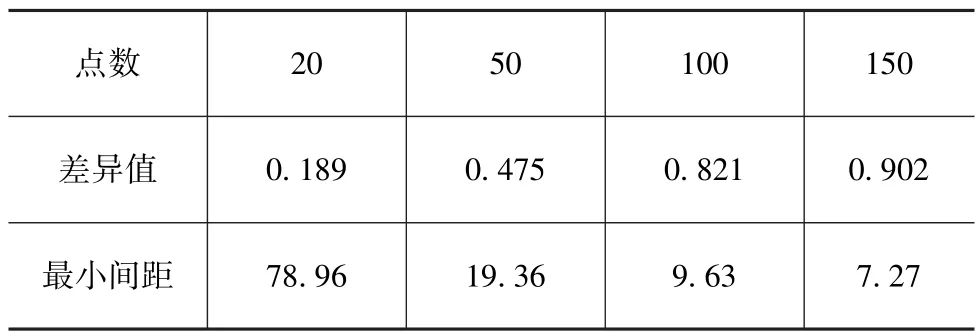
表5 不同试验点数所对应的差异值和最小间距
一般当差异值大于0.5时即满足精度要求,因此各工况点共建立100个试验点。图4为第7工况点的试验点分布图。
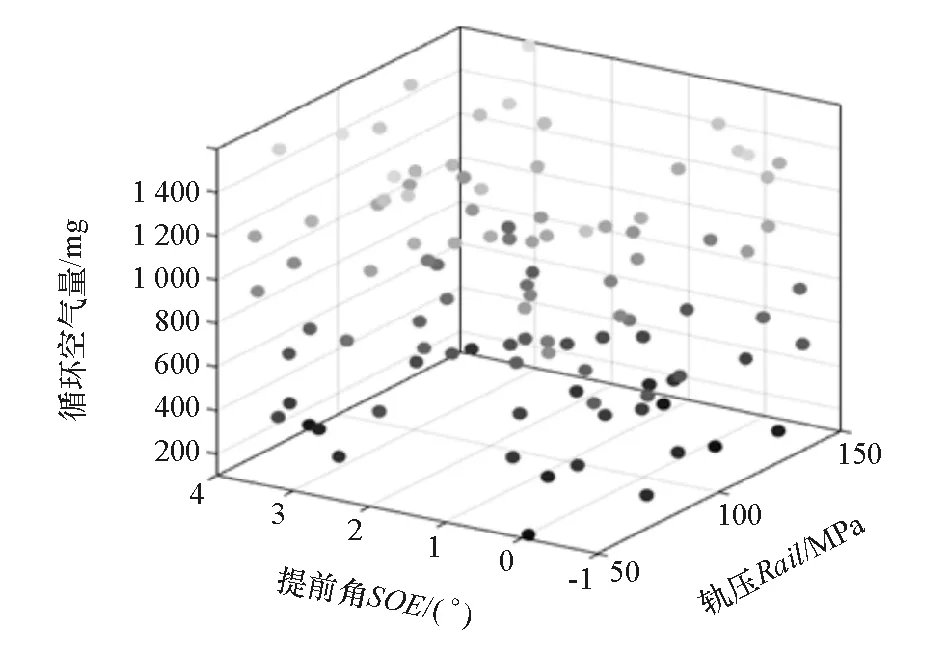
图4 拉丁超立方试验设计
3 响应模型建立
逐点模型的关键是各工况点响应模型搭建,其中发动机输入参数为轨压、提前角和空气量与响应参数油耗、排放和进气温度等之间的映射函数。模型主要方式包括:三次线性函数模型、神经网络和多项式混合径向基函数。对各类模型进行均方根误差分析选出最适合的模型,表6为各工况点对应不同的模型所得到的均方根误差。
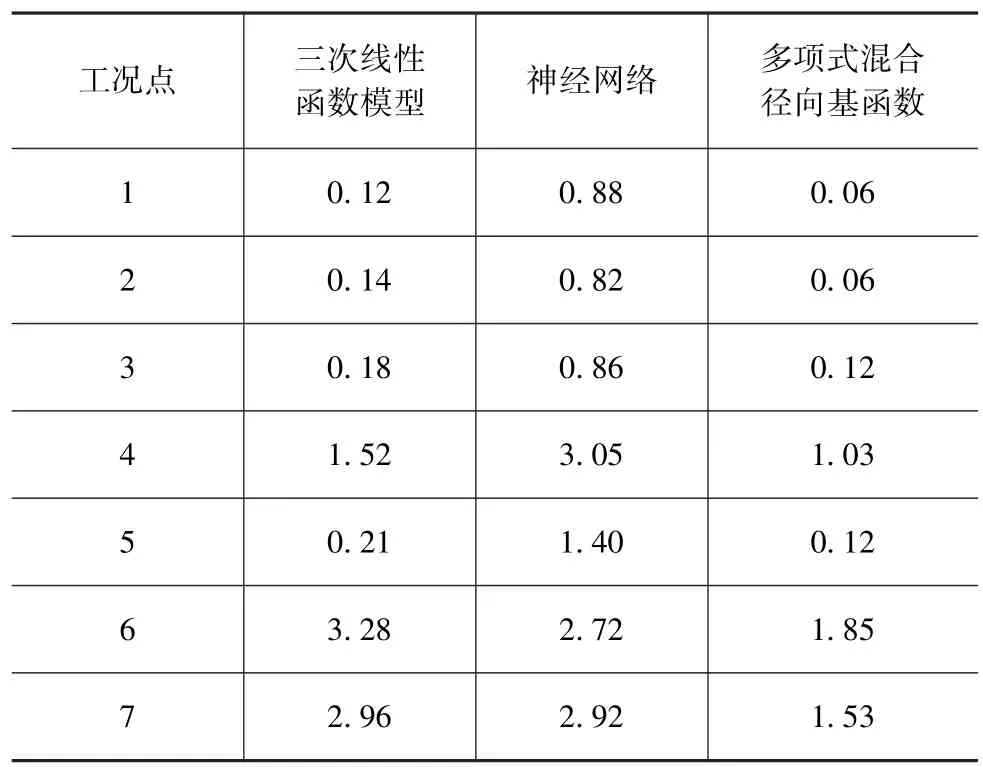
表6 不同模型所对应的均方根误差
从表6中可知2阶多项式混合径向基函数具有最高的模型精度,其表达式为
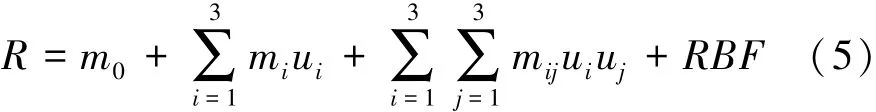
其中
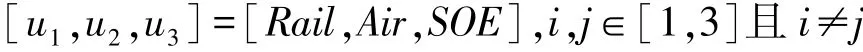
式中mi为多项式系数。
其中径向基函数的传递函数选择高斯函数:
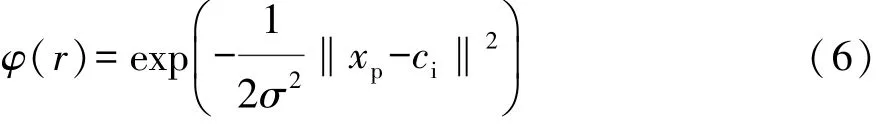
该模型的基本参数见表7。
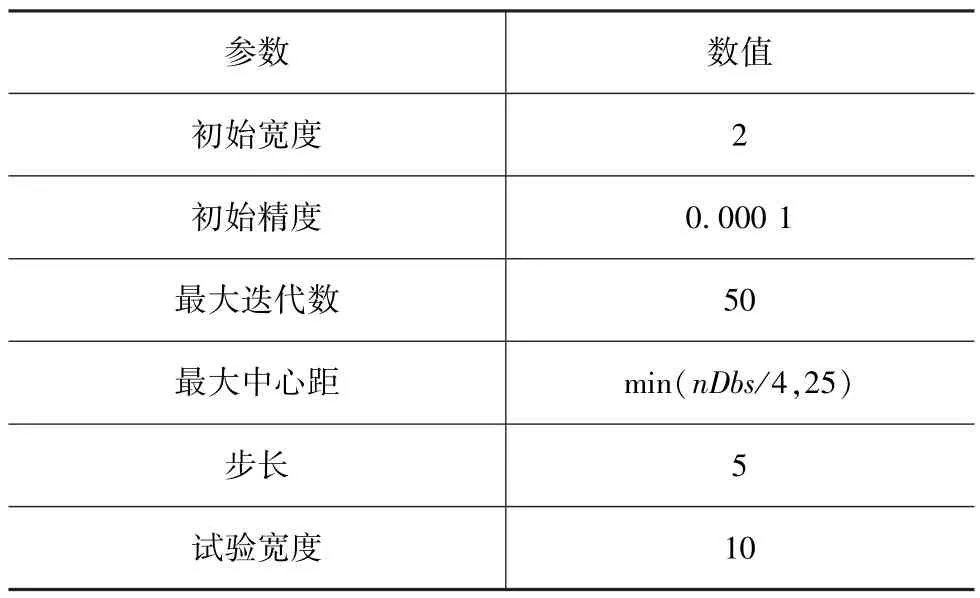
表7 模型设置基本参数
根据式(5)可得发动机对应的油耗(be)、氮氧化合物(NOx)、颗粒物(PM)和进气温度(T2)响应模型。其中第7工况点所对应的响应模型如图5~图8所示。
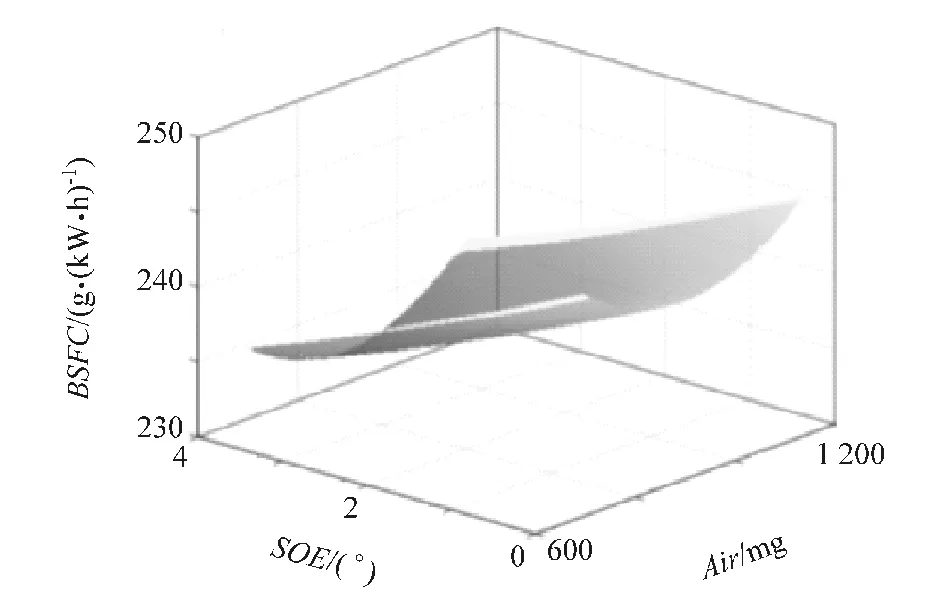
图5 油耗响应模型
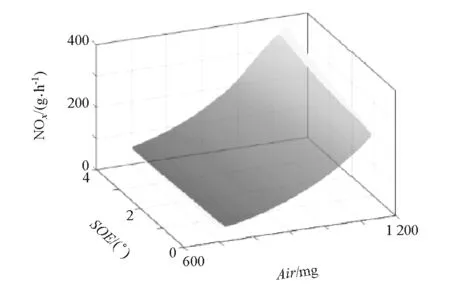
图6 氮氧化合物响应模型
通过响应模型输出校验点输出值与实际台架试验数据进行对比,以氮氧化合物为例,结果见表8。由表可见,拟合值与实际值对比误差均在5%以内,说明该数学模型满足标定精度需求。
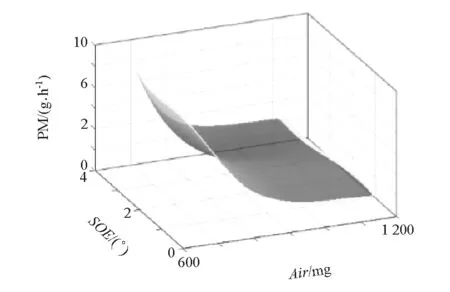
图7 颗粒物响应模型
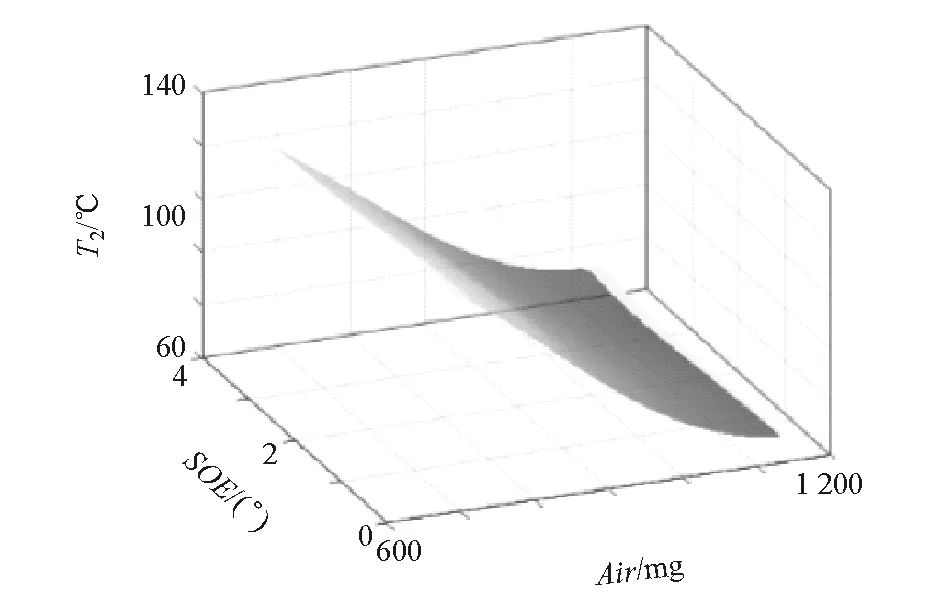
图8 进气温度响应模型
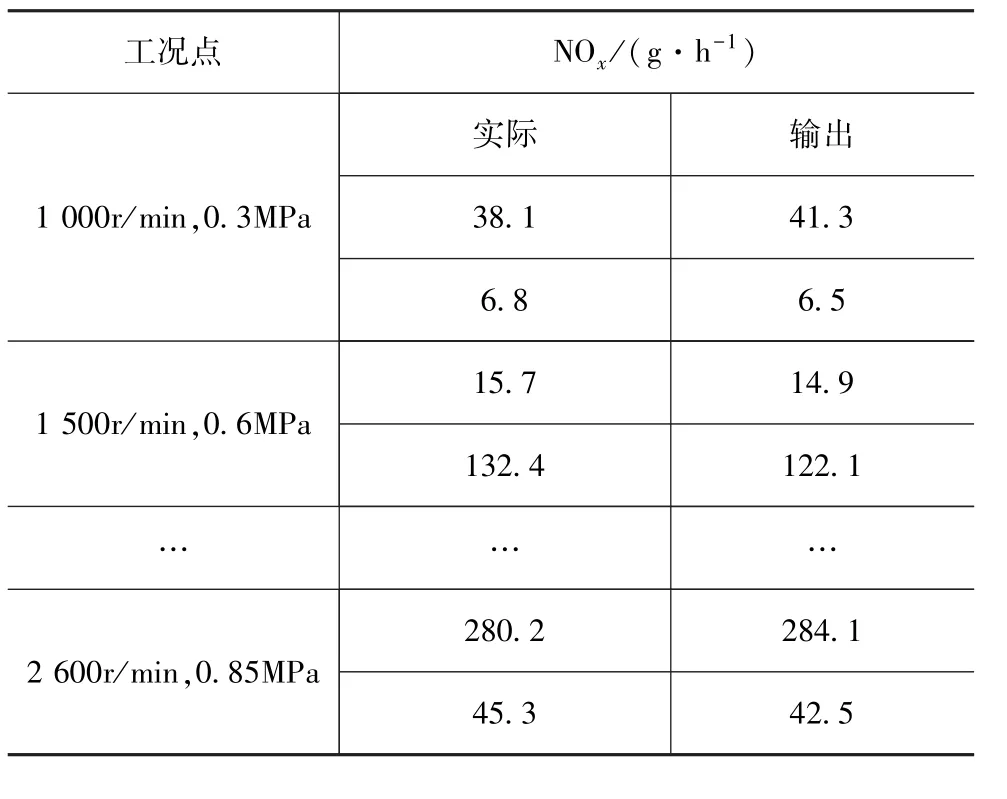
表8 响应模型各点预测对比
4 遗传算法优化
发动机寻优过程属于非线性、不连续的复杂耦合问题,传统的Lagrange乘子法、Monte-Carlo法、黄金分割法均无法使用。而通过模拟自然选择原则的遗传算法(Genetic-Algorithm)可较好的适应多约束、非线性规划的发动机优化问题[11]。
本文中的标定目标是在满足国家排放法规和发动机平稳运行的基础上,优化发动机燃油消耗率。其经济优化数学模型为

式中Be为平均油耗。
以发动机排放5限值和进气温度作为约束模型:

遗传算法优化基本流程:
(1)确定优化模型,同时对输入的参数归一化处理;
(2)设计输入参数的遗传编码,并建立适应度函数;
(3)随机产生初始化群体,并使用响应模型计算对应个体;
(4)计算个体适应度,进行复制、交叉、变异产生下一代种群;
(5)确认是否收敛,若不收敛则重复生成新的群体。
经多次试验选定种群数量为150,遗传算法优化计算的迭代次数为200,交叉概率为0.66,变异概率为0.001。使用Matlab遗传算法工具箱最终可求解出各工况点下发动机燃烧参数最优参数组合,如表9所示。
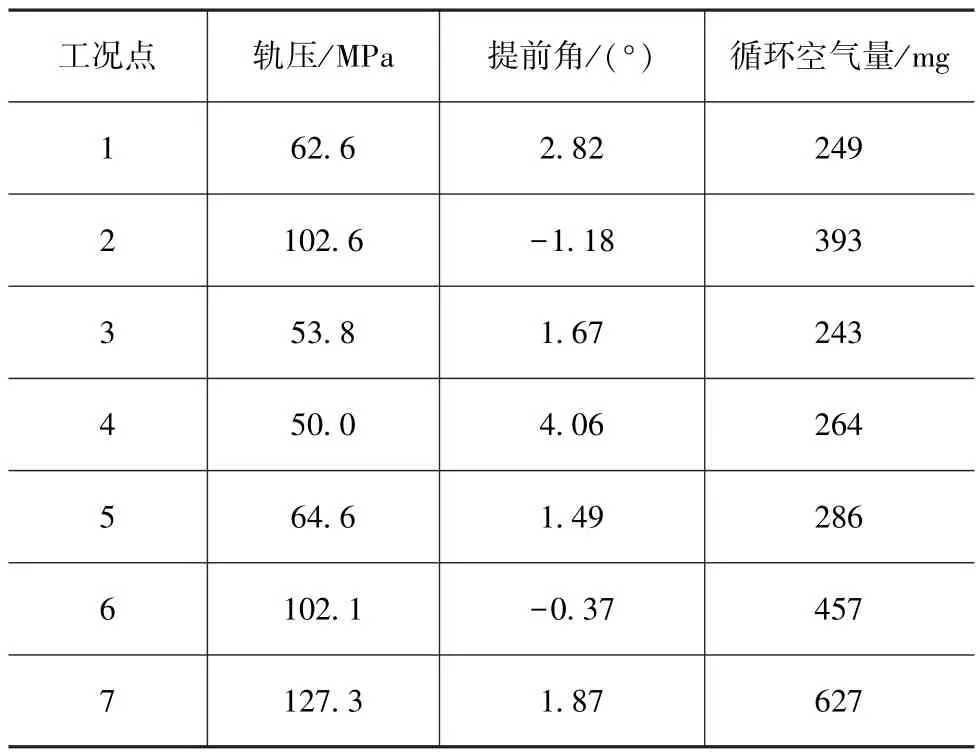
表9 各工况点最优参数
5 最优MAP获取
本次试验发动机采用BOSCH电控ECU,因此需要将平均有效压力转换为对应循环喷油量。
5.1 求解回归方程
在获取各工况点最优参数后,可通过线性拟合获得最优MAP。对于发动机参数一般采用三次多项式拟合,及计算工况点参数与响应参数的三次回归方程,通过回归方程即可求得各参数MAP。其中回归方程如下:
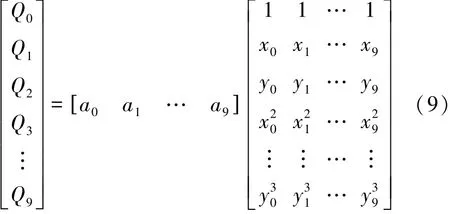
式中:Q为燃烧参数;x为发动机转速;y为发动机循环喷油量;a为常数系数。
将7工况点对应的最优参数,结合边界参数即可求解出三次多项式。分别计算各转速和喷油量所对应的参数,即可绘制出发动机燃烧参数MAP。生成的燃烧参数MAP见表10~表12。
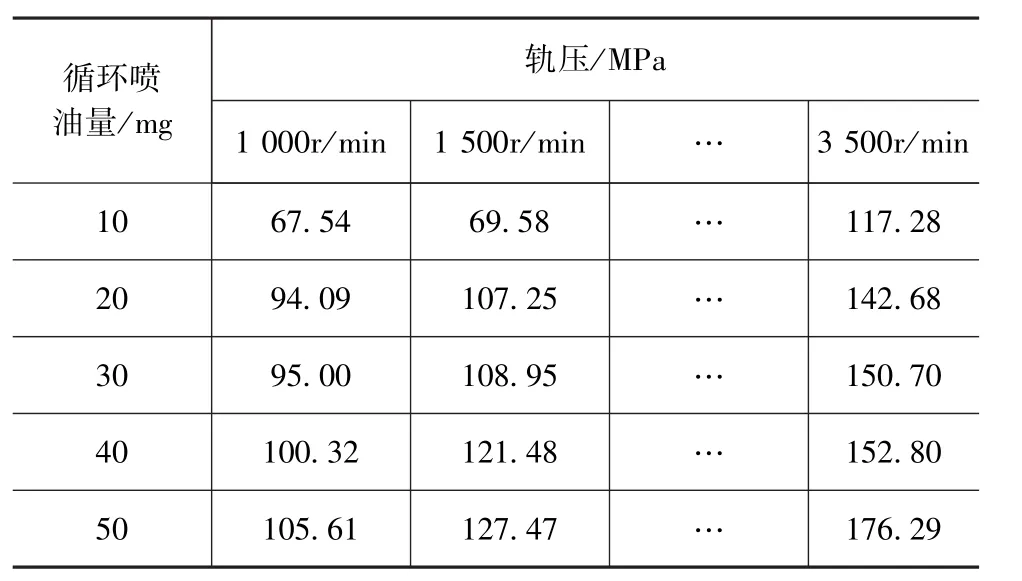
表10 轨压MAP
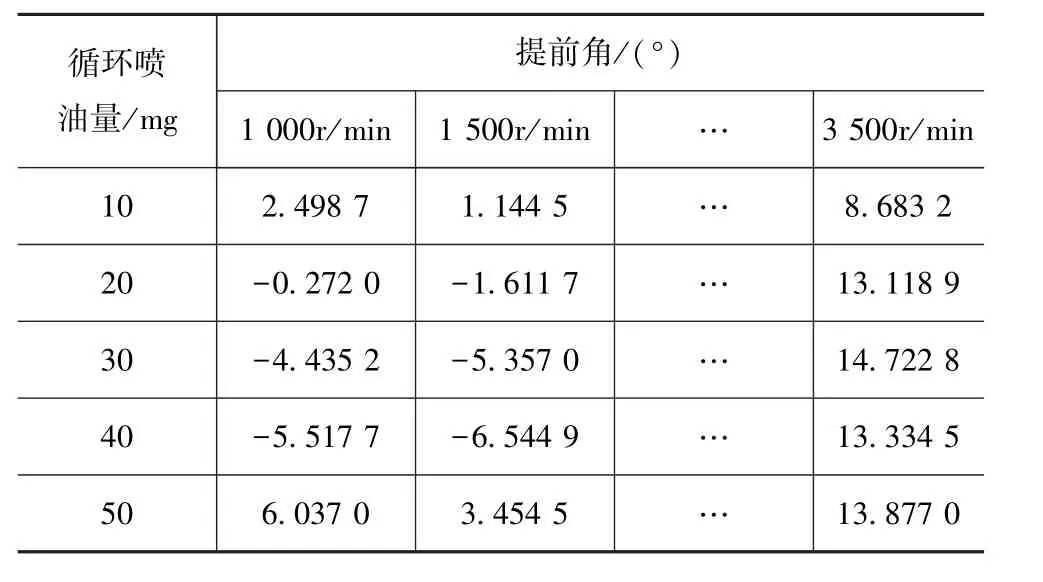
表11 提前角MAP
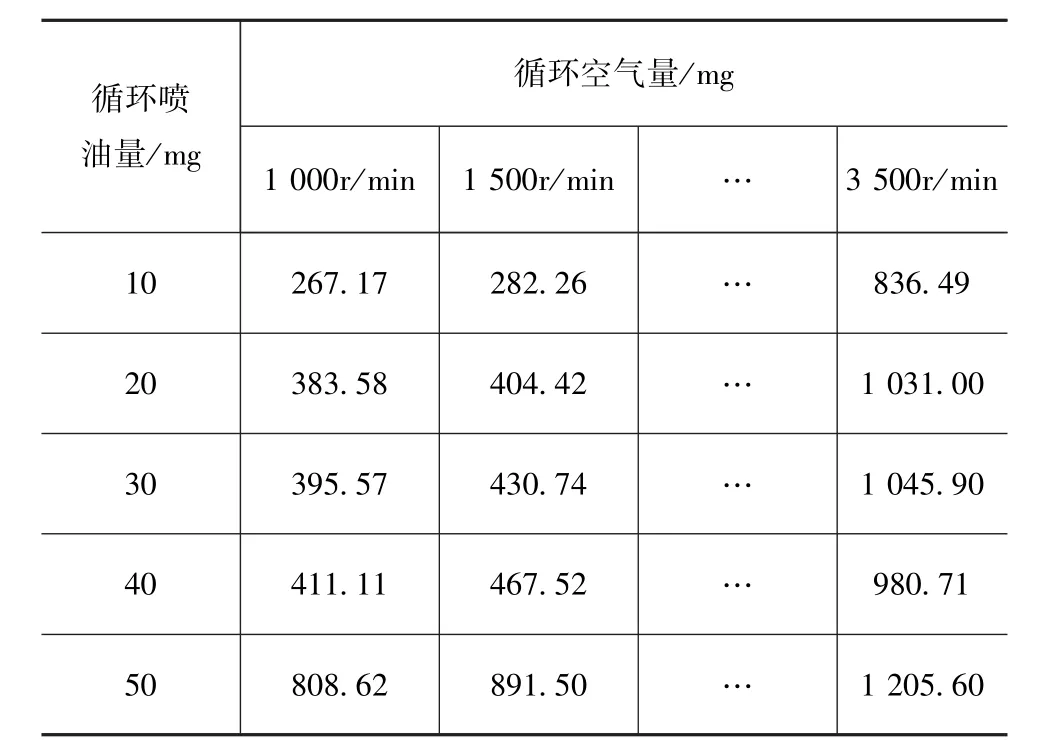
表12 空气量MAP
5.2 基于万有特性对MAP优化
在计算出初始MAP后,使用该参数进行万有特性试验,分析油耗和排放的万有特性曲线。通过分析油耗和排放较高工况区域,对该类区域补充工况点,从而降低整个循环的油耗和排放限值。标定时对参数的修正基本遵循以下基本思路:
(1)空气量越多,燃油燃烧越充分,产生的颗粒物会降低,但由于缸内温度提高会导致氮氧化合物排放的迅速增加;
(2)共轨压力越大,喷油嘴喷油压力会随之增大,燃油雾化效果改善,将改善燃烧效果,因此会降低颗粒物的排放情况,但氮氧化合物的排放会有部分提高;
(3)改变喷油提前角,适当推迟喷油,会改变缸内着火前锋,可降低氮氧化合物的排放,但是会牺牲一定的燃油经济性。
通过上述思路,最终可得到修正后的标定MAP,如图9~图11所示。
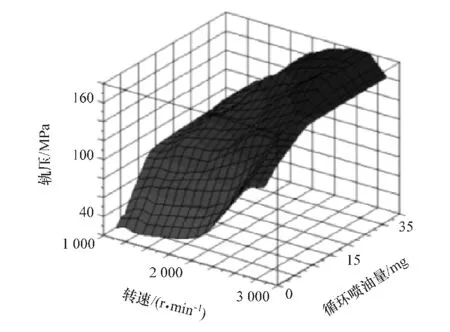
图9 轨压MAP
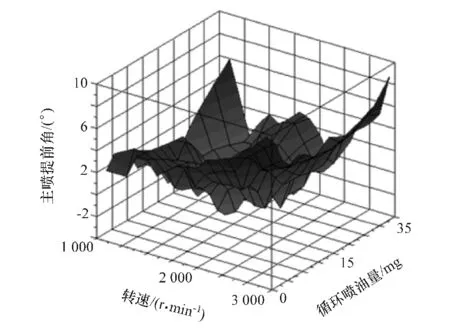
图10 提前角MAP
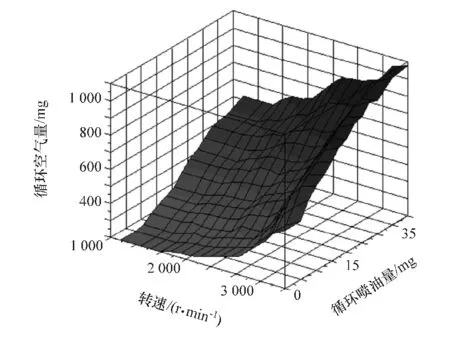
图11 循环空气量MAP
6 MAP验证
根据万有特性试验找出油耗和排放较高的区域,通过增加标定点的方法完成对全局运行空间的优化工作,将最优MAP刷入ECU后,分别通过万有特性试验和整车转鼓试验对其进行验证。
6.1 万有特性试验验证
图12~图14为发动机排放特性图,从中可见,发动机当前在全部运行空间内除了极少数极限工况附近外,整体排放较低。图14为发动机优化特性图,从图中可以看出,发动机除少数低负荷运行空间,整体油耗较低,且在发动机中等负荷范围内油耗较低,可以让车辆在正常运行时保持较低油耗。
6.2 整车转鼓排放试验验证
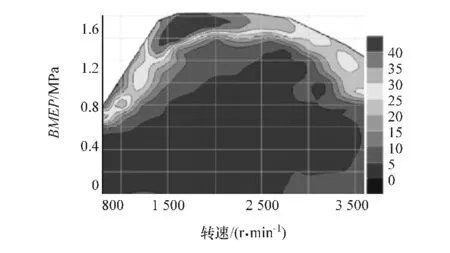
图12 氮氧化合物万有特性曲线(g/kg)
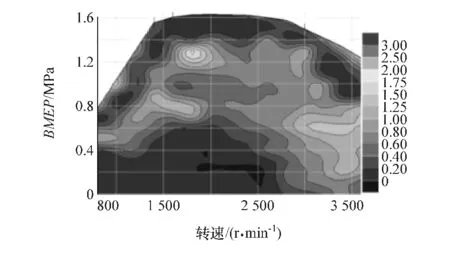
图13 颗粒物万有特性曲线(g/kg)
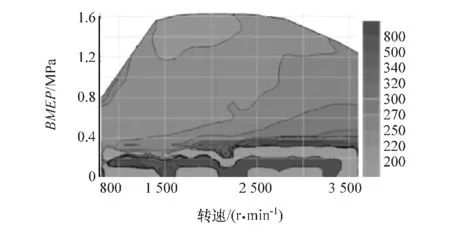
图14 燃油消耗率万有特性曲线(g/(kW·h))
在完成万有特性验证后,为验证标定数据的准确可靠性,需要使用装配相同发动机的车辆进行整车转鼓排放试验,试验结果见表13。从表中数据可以发现,由该模型产生的标定MAP,可使整车满足国五排放法规(试验车辆基准质量大于1 760kg,采用第三级别标准)。同时在 NEDC循环下整车100km油耗为8.15L,相较于9.5L的人工标定,降低了15%,具有较好的燃油经济性。
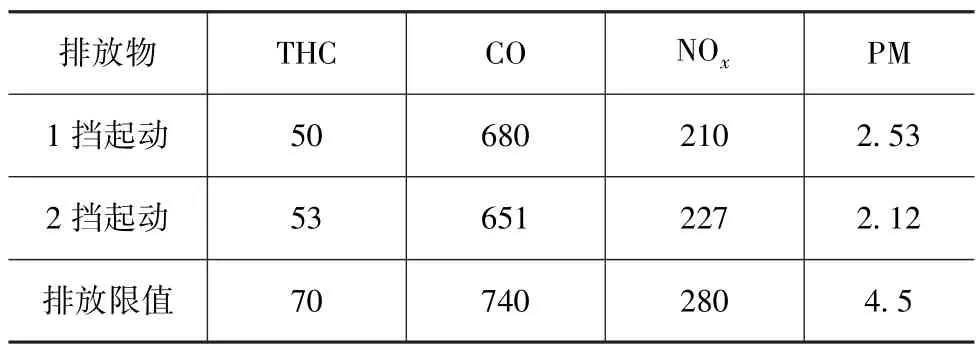
表13 整车转鼓排放参数 mg·km-1
7 结论
(1)空间试验设计能够很好地覆盖发动机工作工况,无需对发动机燃烧参数边界精确了解,适合全新的电控柴油机标定开发,较传统标定方法降低90%标定时间;
(2)通过2阶多项式混合径向基网络搭建的各工况点响应模型具有较好的泛化能力,同时可以达到95%的精度,满足标定需求;
(3)结合万有特性曲线和整车排放试验验证了模型生产的MAP的可靠性,同时可较人工标定降低15%油耗。

