例谈角平分线、平行线、等腰三角形三者关系

江西省瑞金市第六中学 杨 斌

在几何教学中，我们常常会发现图形之间并非孤立的，而是你中有我，我中有你的一种感觉，有时甚至有“我的世界离不开你”的共生共存的依恋之情。而让我们的学生真正能读懂复杂图形中隐含的这种关系，着实是一项必须训练的思维和能力，同时对数学成绩提高有很大的帮助作用。下面我们从人教新版初中数学八年级上册82 页一道课本练习题说起，例谈角平分线、平行线、等腰三角形三者之间的关系。

一、模型来源

例1：如图1，已知AD ∥BC，BD 平分∠ABC。

求证：AB=AD。

证明：∵AD ∥BC，

∴∠ADB ＝∠DBC，

∵BD 平分∠ABC，

∴∠ABD ＝∠DBC，

∴∠ABD ＝∠ADB，

∴AB ＝AD。

结论：角平分线+平分线=等腰三角形。

是否可以这样考虑？如果先有平行、等腰，能否得到平分线呢？于是有了下面的证明。

变式1：如图2，已知AD ∥BC，AB=AD。

求证：BD 平分∠ABC。

证明：∵AB ＝AD

∴∠ABD ＝∠ADB，

∵AD ∥BC，

∴∠ADB ＝∠CBD。

∴∠ABD ＝∠CBD。

∴BD 平分∠ABC。

结论：等腰三角形+平行线=角平分线。

再想：是否先有平分、等腰，然后得出平行呢？于是有如下问题：

变式2：如图3，已知BD 平分∠ABC，AB=AD。

求证：AD ∥BC。

证明：∵AB ＝AD，

∴∠ABD ＝∠ADB。

∵BD 平分∠ABC，

∴∠ABD ＝∠CBD。

∴∠ADB ＝∠CBD。

∴AD ∥BC。

结论：等腰三角形+角平分线 =平行线。

综上，我们可以得出：角平分线、平行线、等腰三角形任意两个做条件，都能得出第三个结论。为了更好地得出基本图形（或者说题根），我们将符合上述特点的基本图及变式图展示如下：

图1

图2

图3

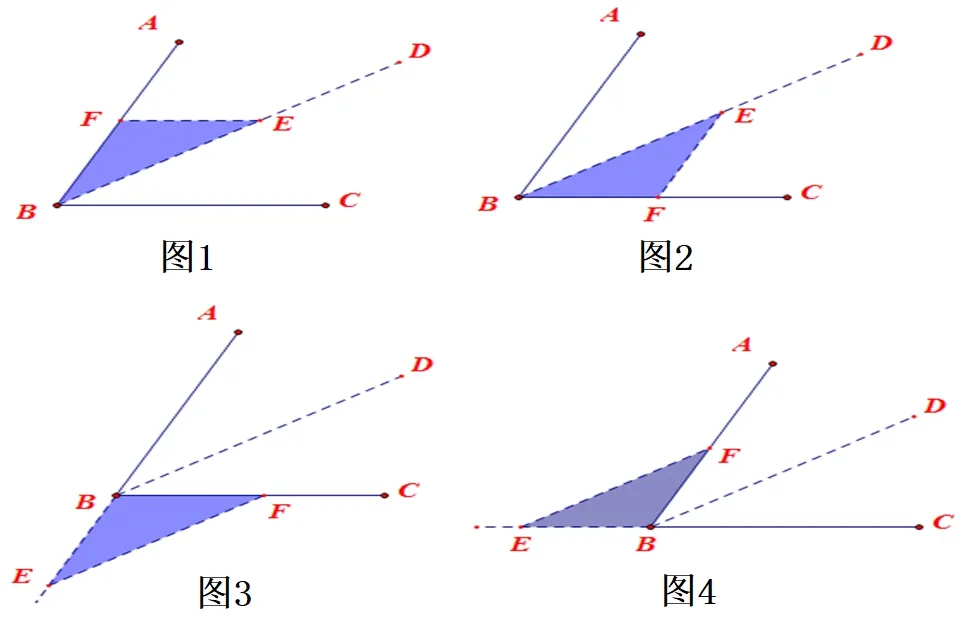
图4

如何更好地找准这样的基本图，产生审题的即认感，我们这样来描述一下：过角平分线上一点作角一边的平行线，与另一边围成的三角形是等腰三角形，或过角一边上的点作角平分线的平行线，与另一边延长线围成的三角形是等腰三角形。

二、典例分析

例2：如图5，在△ABC 中，BO 平分∠ABC，CO 平分∠ACB，MN 经过点O 与AB、AC 相交于点M、N，且MN ∥BC，求证：△AMN 的周长等于AB+AC。

图5

【分析】根据角平分线的定义可得∠ABO ＝∠CBO，根据两直线平行，内错角相等可得∠CBO ＝∠BOM，从而得到∠ABO ＝∠BOM，再根据等角对等边可得BM ＝OM，同理可得CN ＝ON，之后即可求出△AMN 的周长＝AB+AC。

【解答】∵BO 平分∠ABC，

∴∠ABO ＝∠CBO。

∵MN ∥BC，

∴∠CBO ＝∠BOM，

∴∠ABO ＝∠BOM，

∴BM ＝OM。

同理可得CN ＝ON，

∴△AMN 的 周 长＝AM+MO+ON+AN ＝AM+BM+CN+AN ＝AB+AC。

例3：如图6，在△ABC 中，∠C ＝90°，∠BAC 的平分线交BC 于点D，点O 在AB 上，以点O 为圆心，OA 为半径的圆恰好经过点D，分别交AC，AB 于点E，F。试判断直线BC与⊙O 的位置关系，并说明理由。

【分析】连接OD，证明OD ∥AC，即可证得∠ODB ＝90°，从而证得BC 是圆的切线；

【解答】BC 与⊙O 相切。证明：连接OD，如图7。

∵AD 是∠BAC 的平分线，

∴∠BAD ＝∠CAD。

又∵OD ＝OA，

∴∠OAD ＝∠ODA。

∴∠CAD ＝∠ODA。

∴OD ∥AC。

∴∠ODB ＝∠C ＝90°，即OD ⊥BC。

又∵BC 过半径OD 的外端点D，

∴BC 与⊙O 相切。

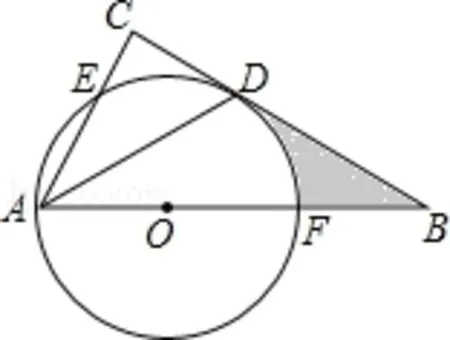
图6

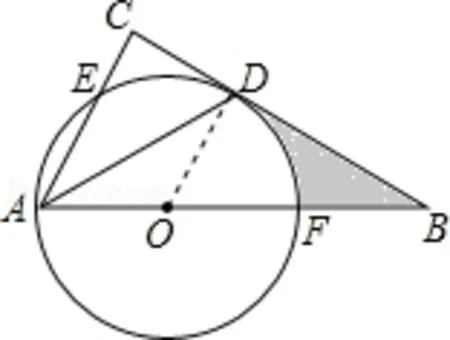
图7