基于改进RSS 测距的拉格朗日优化定位算法*

杨颖辉，杨群亭，高铁杠

（1.河南牧业经济学院信息与电子工程学院，郑州 450045；2.中国民航大学空中交通管理学院，天津 300300；3.南开大学软件学院，天津 300071）

0 引言

无线传感网络（Wireless Sensor Networks，WSNs）系统［1-2］主要应用于人难以涉及的复杂区域事件的监测和数据的采集与传输［3］。而所采集的数据的实用性与其地理位置息息相关，获取了没有准确位置的信息是毫无价值的。然而，在WSNs 网络中，多数传感节点是随机部署，并且多数节点位置是未知的［4］。由于只有已知空间位置的感应数据才具有实用价值，须利用定位技术来估计传感节点的位置。

受硬件条件和无线环境因素的制约，在WSNs中对传感节点的定位仍是一项挑战的工作。目前，已提出多类定位算法［5-6］。依据定位过程是否需要测距，可将这些算法划分测距定位、非测距定位。前者表示在估计未知节点位置时，需要直接估算未知节点离锚节点间的距离，即测距；而后者是通过利用整个网络的连通性估计未知节点的位置。因此，通常测距定位算法精度优于非测距定位算法。

常用于测距定位算法中测距策略有：信号到达角度（Angle of Arrival，AOA）、到达时间（Time of arrival，TOA）、基于接收信号强度（Received signal strength Index，RSS），其中基于RSS 测距是利用未知节点接收到来自锚节点所发射信号的强度估算路径传播损耗，进而估计未知节点离锚节点间的距离。由于基于RSS 测距无需额外的硬件设备，其广泛应用于低成本的无线传感网络WSNs［7-8］。因此，研究并寻求高精度的RSS 测距算法具有重要的实用价值。

然而，基于RSS 测距容易受外界因素干扰，如障碍物、信号反射、散射等，这些因素均增加定位误差。文春武等［9］提出了基于RSS 校正的WSNs 定位算法。先利用高斯函数筛选较准确的RSS 值，再对这些RSS 值设定加权系数，进而估计未知节点的位置。此外，文献［10-11］均利用高斯滤波对RSS 值进行预处理，滤除粗糙的RSS 值，进而提高基于RSS测距精度。类似地，文献［12］利用混合滤波方法处理RSS 值。

在得到测距值后，为了降低定位误差，常将定位过程转换成数学优化问题［13］。文献［14］把定位过程转换成非线性最小平方差的优化问题，降低测距误差，抑制定位误差。而文献［15］分析了利用平方最小平方定位的性能，这给WSNs 的节点定位提供了理论基础。

为此，本文提出基于优化RSS 测距的平方最小平方定位算法（Square-least Square localization algorithm based on improved RSS，SLS-I-RSS）。SLS-I-RSS 算法先改进RSS 测距精度，选用多组锚节点间距离和接收功率作为参考，进而降低测距误差；然后，基于平方最小平方定位算法，建立目标函数，再利用拉格朗日优化目标函数，降低定位的复杂度。实验结果表明，提出的SLS-I-RSS 算法有效地降低定位误差，提高了定位精度。

1 基于RSS 测距

1.1 传统的基于RSS 的测距

在真实的无线环境中，信号易受多径效应、障碍物阻碍、阴影以及反射等影响，导致接收端所接收的信号功率与理想的信号传输模型存在差异。目前，存在3 类信号传播模型：自由空间、Shadowing 和两路径地面反射，其中Shadowing 模型［16］应用最为广泛，且Shadowing 模型如式（1）所示：

其中，β 是路径损耗指数，其可依据环境设定，一般取值范围在2～6。而Pr（d）表示离发送端距离为d 时所接收的信号功率，相应地，Pr（d0）表示离发送端的距离为d0所接收的信号功率，且Pr（d0）和d0为已知值，通常将Pr（d0）和d0称为参考接收功率和参考距离。Xσ表示噪声变量，且为高斯随机变量，其中均值为0，方差表示为σ2。

通过式（1），可推导距离d 的表达式，如式（2）所示：

1.2 基于RSS 测距的改进

然而，式（2）所测量的距离只是依赖于某个参考距离和参考接收功率，这必然会引起测距误差。因此，本文试图选用多组已知节点间距离和相应的接收功率，测量距离，即优化测距参数，进而降低测距误差。

改进后的基于RSS 测距过程如下：首先，假定Bi是未知节点i 通信范围内的锚节点。而表示锚节点Bi的通信范围内的锚节点。若Bi离的距离为dij，它们间的参考接收功率表示为Pij，如下页图1所示。

图1 节点拓扑关系示意图

改进后的基于RSS 测距，就是将Bi作为参考节点，将Bi与间的接收功率为参考功率，即把Pij代替P（rd0）、dij代替d0。利用式（3），估计未知节点i 离锚节点Bi的距离：

其中，Xσj表示Xσ同分布的随机变量。

通常，节点Bi的通信范围内可能存在多个锚节点。假定存在m 个锚节点，且分别表示为，且1≤j≤m。因此，将N 组锚节点的信息（dij，Pi）j代入式（3）可得m 个未知节点i 离节点Bi的距离的对数，且分别表示为。最终，采用均值算法，所估计的未知节点i 离节点Bi的距离的对数等于这m 个对数值的均值，即

2 基于拉格朗日优化的定位算法

图2 改进后的基于RSS 测距与传统基于RSS 测距的不同

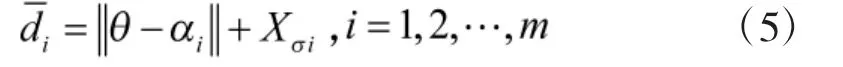
其中Xσi为测距噪声。

先利用平方最小平方算法，建立目标函数：

求解式（6）是一个非线性优化问题，为此对式（6）进行最优转换：

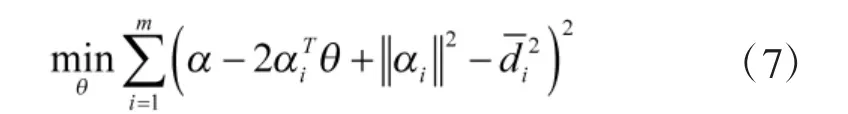
而D 定义如式（10）：

求解式（8）的最优问题属于非凸集优化问题。为此，对式（8）进行变换，减少计算复杂度。因此，将式（8）优化问题转化成规则信任域子问题，并利用拉格朗日进行优化，如式（11）所示：

其中，κ 为实数。

观察式（11）不难发现，计算最优解等价于搜索满足式（12）的值。为此，利用二分法搜索，进而找到满足式（12）的值。然后，再将此代入式（13），便可得到最优解，最后可得到未知节点位置估计值。

3 仿真以及性能分析

3.1 仿真环境

利用MATLAB 建立仿真平台，分析SLS-I-RSS的定位算法，利用均方定位误差（Mean Location Error，MLE）作为性能指标。所谓MLE 是指多次测量的Δθ 的平均值，其中定位误差Δθ：

网络内有N=100 个节点分布于100 m×100 m区域内，其中锚节点数m=40 个。节点的传输半径为20 m。每次实验独立重复50 次，取平均值作为最终的仿真数据。

3.2 数据分析

在实验过程中，分别考查路径损耗β、噪声变量Xσ以及锚节点数m 对MLE 的影响。同时，选用文献［17］所采用的基于RSS 差分校正的最小二乘-拟牛顿定位算法作为参考，记为RSS-DLN。

3.2.1 路径损耗β

假定Xσ=2，路径损耗β 从2 变化4.5。在这个变化过程中，定位算法的MLE 如图3 所示。从图4 可知，MLE 随路径损耗β 的增加而提升。这主要是因为：路径损耗β 的增加，提高了测距误差，这必然增加定位误差，最终，增加了MLE。

此外，与RSS-DLN 定位算法相比，提出的SLS-I-RSS 算法的MLE 得到有效下降。这说明，SLS-I-RSS 算法的定位精度优于RSS-DLN，并且随β 的增加，优势越发明显。例如，在β=2.0 时，RSSI-DLN 的MLE 达到1.1 m，而SLS-I-RSS 算法的MLE 只有0.9 m。当β 从2.0 增加至4.5 时，RSSI-DLN 和SLS-I-RSS 算法的MLE 分别增加至3.5 m、1.75 m。与RSS-DLN 相比，SLS-I-RSS 算法的MLE 下降了约49.7%。

3.2.2 噪声变量Xσ

在实际环境中，噪声变量Xσ对定位精度有直接的影响。为此建立实验，分析Xσ对MLE 的影响。在本次实验中，β=3、m=40、N=100，而Xσ在［1.0，5］间变化。实验数据如图4 所示。

从图4 可知，噪声变量Xσ的增加提高了MLE。相比于RSSI-DLN 定位算法，提出的SLS-I-RSS 定位算法降低了MLE。这主要是因为SLS-I-RSS 算法改进RSS 测距精度，同时，利用拉格朗日最优估计未知节点的位置，降低了定位误差。

3.2.3 锚节点数m

本次实验分析锚节点数m 对MLE 的性能影响，其中噪声变量Xσ为2 dB，路径损耗β=3。锚节点数m 从20 变化至40，实验数据如图5 所示。

图5 锚节点数m 对MLE 的影响

从图5 可知，锚节点数m 的增加降低了MLE，提高了定位精度。原因在于锚节点数越多，在测距时，能够选择更多组的锚节点间距离和参考接收功率，进而降低了测距误差。最终能够提高定位精度。

3.3 算法复杂度

利用算法运行时间反映算法的复杂度。运行时间越长，算法越复杂。为此，建立分析定位算法的实验。在实验中，噪声变量Xσ为2 dB，路径损耗β=3。锚节点数m=40。RSSI-DLN 和SLS-I-RSS 算法的运行时间如表1 所示。

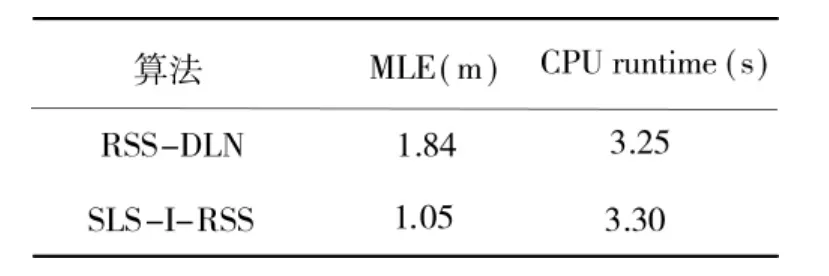
表1 算法的运行时间

从表1 可知，提出的SLS-I-RSS 算法的MLE远低于RSSI-DLN，而算法运行时间只是略高于RSSI-DLN 算法的0.05 s。换言之，SLS-I-RSS 算法并没有以增加复杂度为代价换取定位精度。

4 结论

针对无线传感网络的节点定位问题，提出基于优化RSS 测距的平方最小平方定位算法SLS-I-RSS。SLS-I-RSS 算法充分考虑了RSS 测距误差，并利用多组锚节点间距离和接收功率作为参考，估计未知节点离锚节点间的距离。然后，利用平方最小平方算法优化定位问题。实验结果证实提出的SLS-I-RSS 算法能够有效地降低定位误差。