组合粗差探测的MHSS ARAIM算法

张亚彬，王 利，范丽红，曲轩宇

1. 长安大学地质工程与测绘学院，陕西 西安 710054； 2. 地理信息工程国家重点实验室，陕西 西安 710054； 3. 地理国情监测国家测绘地理信息局工程技术研究中心，陕西 西安 710054

由于GPS系统历史中出现过多次信号干扰事件[1]，致使用户对导航系统的完好性产生担忧。为了避免这种情况引发的严重后果，导航系统的可靠性与完好性监测显得尤为重要。完好性监测可以分为系统级监测和用户级监测。其中，用户级完好性监测为接收机自主完好性监测算法[2](receiver autonomous integrity monitoring，RAIM)。该算法基于冗余观测信息，无须增加外部辅助手段，可独立用于导航中的卫星故障检测和识别，从而保证用户完好性性能[3]。但RAIM算法仅适用于航行的非精密进近阶段，无法满足精密进近阶段的需求，故在其基础上衍生出了ARAIM算法[4-7]，该算法可独立保证航行精密进近阶段系统的可靠性与完好性。ARAIM算法主要分为扩展的ARAIM(extended-ARAIM，EARAIM)[8]、相对RAIM(relative RAIM，RRAIM)[9]、MHSS ARAIM[10-12]3类。其中，EARAIM能够提高单星座ARAIM算法的可用性，但算法复杂，其合理性和实用性有待进一步验证；RRAIM能在完好性通道告警反应时间内保证用户完好性，但需要进行周跳探测、模糊度固定等，实现较为复杂；MHSS ARAIM算法满足航行LPV-200进近阶段的完好性监测要求且容易实现，但存在计算子集过多、计算量过大等不足。

在粗差探测与剔除方面，自文献[13]提出数据探测法后，拟准平差法[14]、丹麦(Danish)法[15]、稳健估计法[16-18]等相继被提出。随后，有学者将粗差探测与剔除方法应用于RAIM算法中。其中，拟准平差法可用于RAIM多故障探测与隔离，但其可靠性、准确性还需进一步验证[19]；基于信噪比的Danish法能提高RAIM性能，但其参数存在不确定性，理论性不够强[20]；稳健估计法能降低粗差值对定位精度的影响，从而提高RAIM性能[21]。目前，粗差探测与剔除方法应用于ARAIM算法中的相关文献较少。因此，为了弥补ARAIM算法在原始数据粗差探测与剔除方面的不足，本文提出了一种组合粗差探测的MHSS ARAIM算法，并使用GPS和BDS观测数据分析其在航行LPV-200阶段的性能。

1 MHSS ARAIM算法

MHSS ARAIM算法即基于MHSS的ARAIM算法[22-25]。该算法通过扩展传统分组解法和运用多种假设法对完好性风险进行评估，在多个独立和相关卫星故障条件下考虑多卫星星座的伪距测量值，通过最优分配连续性和完好性风险来计算垂直保护级，以检验其是否满足航行阶段要求。

考虑一般的线性化观测方程

L=AX+Δ

(1)

基于式(1)进行如下假设

假设H1,i成立，则第i个观测值含有故障。则从式(1)中剔除第i个观测值后，得到观测方程

L(i)=A(i)X+Δ(i)

(2)

式中，i为读取伪距观测值时赋予的序号，并将卫星号与相应的观测值序号对应存储，以便后续进行有关剔除工作。

利用最小二乘法，由式(1)可得X估计值x(0)

x(0)=S0L

(3)

x(i)=S(i)L

(4)

式中，S(i)=(ATMiWURAA)-1ATMiWURA；Mi为第(i,i)元素为0的单位矩阵。

结合式(3)和式(4)可得判断第i颗卫星是否发生故障的检验统计量

d(i)=xz(i)-xz(0)

(5)

且探测阈值为

(6)

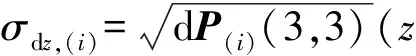
不含故障时的用户保护水平值为

(7)

第i颗卫星含潜在故障时的用户保护水平值为

(8)

最终的用户保护水平为

VPL=maxVPL0,maxVPL(i)
(i=1,2,…,n)

(9)

2 粗差探测与剔除

一般可通过残差值判断观测值中是否含有粗差。主要在最小二乘残差基础上采用整体和局部两种检验方法来探测和剔除粗差[28]，其中整体检验用于探测观测值中是否含有粗差，若含有粗差，则采用局部检验将粗差识别并剔除。

2.1 整体检验

(10)

式中，m为所求未知数个数，一般为4；n为观测值个数；α为误警率；W为权阵，v为残差值。

在整体检验中，可作如下假设

若H0成立，则说明观测值不含粗差，可以进行MHSS ARAIM无故障相关计算；当满足H1时，则需要寻找含粗差的观测值，即局部检验。

2.2 局部检验

可以通过残差值来测试伪距观测值的局部一致性，并识别与剔除含粗差的观测值。残差值标准化后为

(11)

式中，wi为标准化残差；Qvvii为残差协因数阵Qvv的第i个对角元素；残差协因数阵公式如下

Qvv=Q-A(ATGA)-1AT

式中，Q为伪距观测值的协因数阵，且Q=G-1。

若冗余观测值足够多，则可以通过标准化残差wi识别出含粗差的观测值。由前面假设残差值服从正态分布可知，若观测值不含粗差，则wi服从标准正态分布；反之，则wi将服有偏正态分布，可作如下假设

若H0,i成立，表明第i个观测值不含粗差；反之，表明第i个观测值含有粗差。若观测值中只含有一个粗差值，则最大的wi对应的观测值即为粗差值，将其剔除并进行MHSS ARAIM单故障相关计算；如果含有多个粗差值，需要循环局部检测逐步剔除，并进行MHSS ARAIM多故障相关计算。

组合粗差探测的MHSS ARAIM算法流程如图1所示。

图1 组合粗差探测的MHSS ARAIM算法流程Fig.1 Flow chart of the MHSS ARAIM algorithm combined with gross error detection

算法流程如下：

(5) 若存在多个粗差值，需要循环步骤(3)、(4)。

由此可见，将粗差探测方法与MHSS ARAIM算法进行组合，不仅能弥补MHSS ARAIM算法的不足，而且能进一步保证MHSS ARAIM算法使用数据的可靠性，为提高MHSS ARAIM算法的性能提供了可能。

3 算例分析

3.1 粗差探测与剔除性能分析

为了验证粗差探测与剔除方法对定位精度的改善效果，采用IGS CHAN站第228天采样间隔为30 s的GPS伪距观测数据，使用L1、L2双频无电离层进行定位，设计如下3种方案：

(1) 伪距单点定位计算。

(2) 含有粗差的伪距单点定位计算(每隔10历元对任意一颗卫星在L1伪距观测值上添加20 m/30 m/40 m/50 m误差，以模拟卫星信号突发故障情况)。

(3) 粗差探测与剔除。

根据3种方案进行数据处理。由于篇幅限制，本文只给出添加50 m粗差的定位结果，如图2所示。表1给出添加不同类型粗差的检测与剔除结果统计。

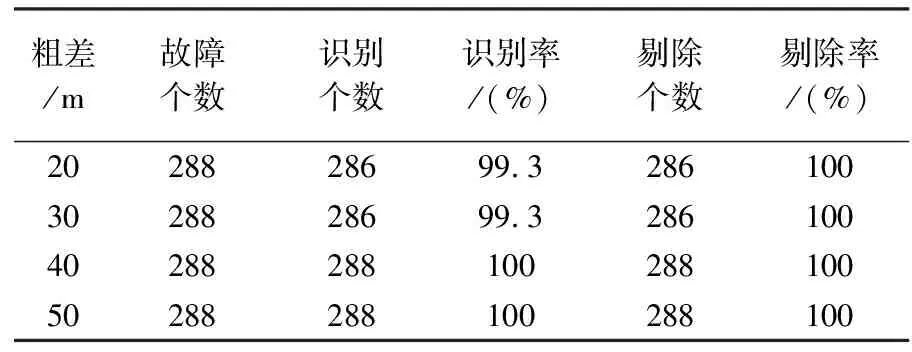
表1 粗差探测与剔除结果统计

图2从左到右分别为正常定位结果、添加粗差定位结果、剔除粗差定位结果。图中绿色、蓝色和粉色分别代表X-Z面、Y-Z面和X-Y面的偏差值。对比图2(a)与(b)可知，添加50 m粗差的定位结果分布明显离散，误差量级约为40 m；对比图2(b)与(c)可知，使用粗差探测与剔除方法后定位结果明显相对集中，误差量级约为6 m；对比图2(a)与(c)可知，使用粗差探测与剔除方法后定位结果与原始数据定位结果大体相似，误差量级约为6 m，个别点定位结果存在差异且不大。

由表1可知，添加40、50 m粗差时，使用粗差探测与剔除方法均能准确识别并剔除粗差。而添加20、30 m粗差时，存在2个历元未识别粗差，其最小可探测偏差分别为17、16 m，原因为卫星高度角过低，分别为4.2°、4.5°。将粗差添加到该历元卫星高度角较高的观测值上时，均能被识别和剔除。由此可知，使用该粗差探测与剔除方法能够有效检测与剔除粗差，提高了定位精度。

3.2 组合粗差探测的MHSS ARAIM算法性能分析

选取采样间隔为30 s且未添加粗差的IGS URUM、SHAO、CHAN站2016年第228天GPS双频伪距观测值及iGMAS KUN1、BJF1站2015年第16天BDS双频伪距观测值进行组合粗差探测的MHSS ARAIM算法性能分析。针对航行LPV-200阶段，其中先验参数设置[6,12]如表2所示，使用MHSS ARAIM与组合粗差探测的MHSS ARAIM算法分别进行数据处理。设计如下两个方案：

方案1：假设存在单故障卫星情况。

方案2：假设存在双故障卫星情况。

由于5个测站结果相似且限于篇幅，方案1只给出GPS URUM站(图2)与BDS KUN1站(图3)的处理结果。表3统计了5个测站方案1的处理结果。

由图3、图4可知，可见卫星数均在7～13颗，满足MHSS ARAIM算法需求。在单故障假设下，组合粗差探测MHSS ARAIM算法的VPL、EMT整体略优于MHSS ARAIM算法。该算法对GPS的改善效果略优于BDS。

表2 参数设置

由表3可知，组合粗差探测的MHSS ARAIM算法的EMT、VPL均值略优于MHSS ARAIM算法；与MHSS ARAIM算法相比，组合粗差探测的MHSS ARAIM算法在5个测站上对EMT的精度依次提高了37.09%、17.24%、13.08%、8.33%、10.94%，对VPL的精度依次提高了32.49%、32.23%、32.12%、13.64%、12.32%。

表3 单故障结果统计

受篇幅所限，方案2只给出GPS URUM站(图5)与BDS KUN1站(图6)的处理结果。表4统计了5个测站方案2的处理结果。

图2 添加50 m粗差时3种方案的伪距单点定位结果对比Fig.2 The comparison of results from three schemes of single point positioning with gross errors (50 m)

图3 单故障下URUM站的结果Fig.3 Results of URUM under single failure

图4 单故障下KUN1站的结果Fig.4 Results of KUN1 under single failure

由图5、图6可知，在双故障假设下，组合粗差探测的MHSS ARAIM算法的EMT、VPL均略优于MHSS ARAIM算法；该算法对GPS观测数据的改善效果略优于BDS。

由表4可知，组合粗差探测的MHSS ARAIM算法计算出的EMT、VPL均值略优于MHSS ARAIM算法；与MHSS ARAIM算法相比，组合粗差探测的MHSS ARAIM算法在5个测站上对EMT的精度依次提高了80.04%、86.71%、75.79%、33.33%、26.44%，对VPL的精度依次提高了50.63%、47.61%、50.73%、19.49%、16.99%；同时，发现个别测站上还存在过大的VPL值(160.63 m)，其原因主要是因为卫星几何构型过差。

由上述结果分析可知，组合粗差探测的MHSS ARAIM算法对BDS观测数据的改善效果略低于GPS，可能原因为：①MHSS ARAIM算法的先验参数更加适用于GPS数据；②BDS观测数据的定位综合精度低于GPS。从整体上看，组合粗差探测的MHSS ARAIM算法性能优于MHSS ARAIM算法。

图5 双故障下URUM站的结果Fig.5 Results of URUM under double faults

图6 双故障下KUN1站的结果Fig.6 Results of KUN1 under double faults

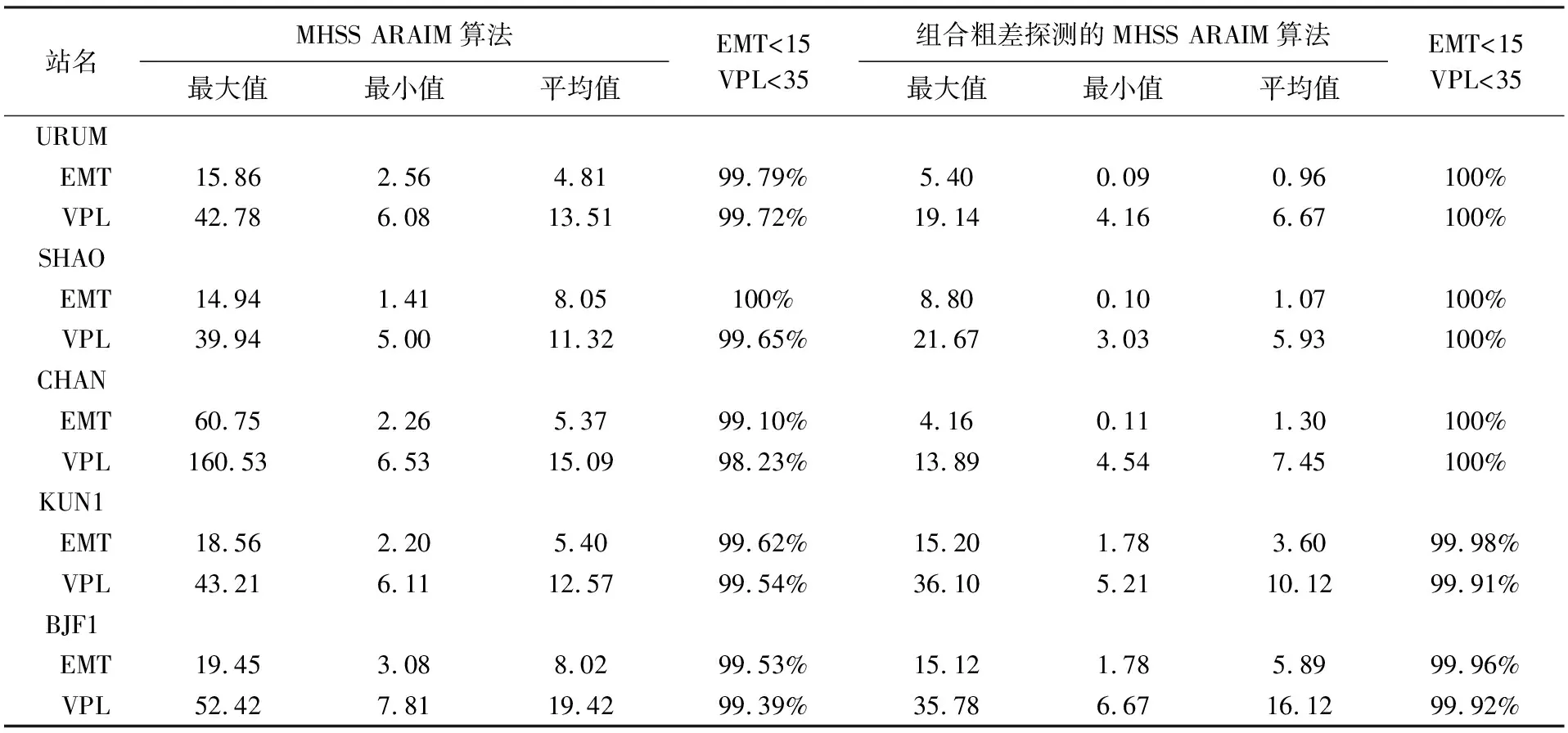
表4 双故障结果统计

4 结 论

本文提出了一种组合粗差探测的MHSS ARAIM算法。该算法先用粗差探测方法对原始数据进行粗差识别与剔除，而后用MHSS ARAIM算法处理经粗差探测后的数据，并通过试验分析了该算法分别应用于GPS和BDS导航的性能。计算和分析结果表明：该算法分别应用于GPS和BDS导航时，在单故障假设下，EMT的精度分别提高了22.47%、9.63%，VPL的精度分别提高了32.28%、12.98%；在双故障假设下，EMT的精度分别提高了80.85%、29.88%，VPL的精度分别提高了49.66%、18.24%。此外，组合粗差探测的MHSS ARAIM算法可有效改善MHSS ARAIM算法中存在的抗差能力弱、计算子集过多、计算量过大等不足。但是，组合粗差探测的MHSS ARAIM算法应用于多频多星座观测数据的效果和性能尚有待进一步研究。