基于极球面投影的极区格网等角航线

刘文超，卞鸿巍

1. 中国人民解放军91550部队，辽宁 大连 116023; 2. 海军工程大学，湖北 武汉 430033

中低纬度地区航海中通常采用等角航线[1]。但在高纬度地区，等角航线曲率较大、航程较长。因此，等角航线不再适用于极区航行[2]，极区航行通常采用大圆航线[3]。但是大圆航线上地理航向角快速变化、极区定向误差较大等问题不利于极区航行控制，为此1941年英国皇家空军Maclure中校结合极区极球面投影提出了极区格网导航技术[4]，使得大圆航线、格网导航技术和极球面投影配合使用成为一种早期解决极区航行问题的方案[5]。随着现代航海对精度和安全性的更高需求，早期极区航行方案也需要优化。对该方案进行分析主要存在以下4个问题：①大圆航线在极球面投影图上投影为非直线，会引起固有的航行绘算误差，文献[6—8]分别就该问题研究了极球面投影图上大圆航线近似为直线引起的定位和定向误差，虽然认为该误差较小，可以简化近似处理，但是该近似处理原理性误差依旧存在，并不能完全消除；②极区航向采用格网航向角，大圆航线上的格网航向角并不相等[9]，单一航线上格网航向角的不规则变化必然不利于航行控制[10]；③严格执行大圆航线，只能采用航迹舵执行[11]，无法像中低纬度地区按照等航向角的规则采用航向舵来执行[12]；④大圆航线基于地球球体模型，必然会存在采用地球模型引起的原理性误差[13]，虽然文献[14—16]分别研究的基于地球椭球模型的大椭圆航线可以解决该问题，但依然存在上述3个问题。因此，大圆航线、格网导航技术和极球面投影无法达到精确配合应用。而中低纬度地区，等角航线上地理航向角相等且在墨卡托投影图上投影为直线[17]，能够与导航技术(导航设备)、墨卡托投影精确配合实现航行。为此，本文借鉴中低纬度地区等角航线的设计思想，提出一种在极球面投影图上表现为直线的“等角航线”——格网等角航线，并对其航线方程、航向角和航程计算方法进行了研究。

1 极区极球面投影及格网导航

1.1 基于双重投影的极区极球面投影方法

高精度的地球模型近似为一个旋转椭球体，将地球椭球面直接按照极球面投影方法投影到平面上较为困难[18]。双重投影[19]是一种解决方法，即先将椭球面等角投影到球面上，再将球面按照极球面投影方法投影到平面上。考虑到北极经线快速收敛于极点，北极投影图中经度跨度较大甚至涵盖所有经线，椭球面在球面上的等角投影宜采用完整等角投影方法，其投影变换公式[20]为

(1)

式中，φ、l为球面纬度、经度；φ、λ为椭球面纬度、经度；R为球体半径；RN为卯酉圈曲率半径；ω1为投影角度变形；φ0、φ0、RN0分别为基准椭球纬度、球体纬度及基准位置处的卯酉圈曲率半径。

将椭球面等角投影到球面后，利用极球面投影的方法将球面等角投影到平面上。极球面投影是一种透视方位投影，其视点位于地球极点上，如图1所示。具体投影变化公式[21]如下

(2)

式中，ρ为纬线投影半径；δ为两经线间的经差；Z和σ为球面坐标；Z0为基准位置处的球面坐标；ω2为投影角度变形。

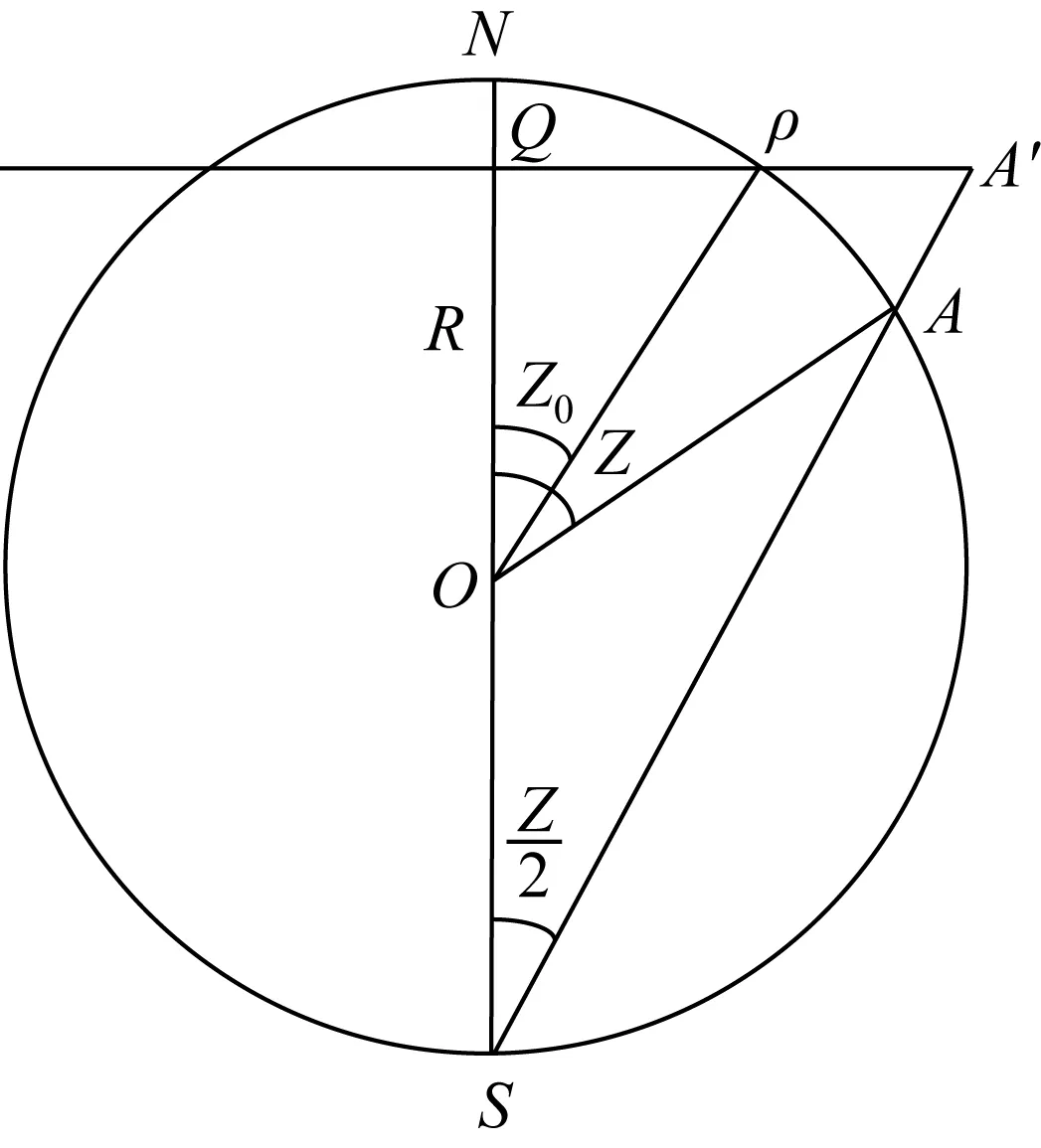
图1 极球面投影示意图Fig.1 Diagram of polar stereographic projection

式(1)和式(2)共同构成了基于双重投影的极区椭球极球面投影变换方法，按照该变换公式得到的投影仿真图如图2所示。分析式(1)和式(2)可得该投影方法的两条性质：①该投影为等角投影，满足载体航行投影图为等角投影的条件[22]；②该投影上经线方程和纬线方程分别为

(3)

因此，经线投影为以极点为中心的一族放射线，纬线为一族同心圆，投影曲线规则便于量测航向和距离，适合航行人员航行绘算。

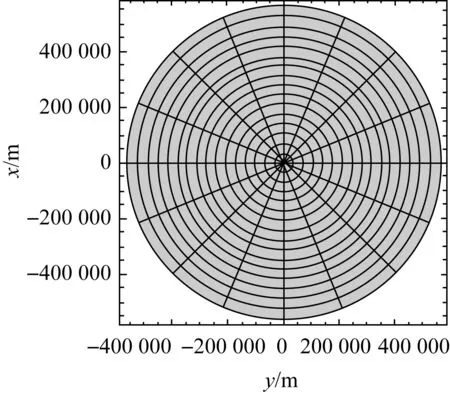
图2 椭球极球面投影仿真图(纬度85°N—90°N) Fig.2 Simulation of ellipsoidal polar stereographic projection

1.2 格网导航方法

载体通常采用大圆航线进行极区航行。地理真航向以收敛于极点的地理经线作为航向参考基准。由于经线在极区快速收敛导致采用大圆航线航行时航向变化较快，不便于极区航行监控和航行绘算，且极区很小的经纬误差会导致很大的航向误差，影响航行安全。为此，本文研究和提出了一种格网导航方法[4]。该方法的基本思想就是在极区投影图上绘制格网线作为极区航向基准。具体是在极球面投影图上选择某条经线，通常为0°经线，在图上绘制平行于0°经线的格网线，沿每条格网线与0°经线正北方向相同的方向表示成0°GD(grid direction)，相反方向表示成180°GD，格网0°GD称为格网航向基准[23]，如图3所示。那么，任意位置点M的地理航向角ψt与格网航向角ψG的转换关系为

ψG=ψt-λ

(4)

但是大圆航线在极球面投影图上并不完全是直线，均不能达到中低纬度等角航线在墨卡托投影完全表现为直线，方便航行操纵和绘算的理想程度。因此需要研究一种在极区投影图上表现为直线的航线，可以与格网导航技术精确配合使用。

2 格网等角航线定义及航线方程

借鉴中低纬度地区等角航线、墨卡托投影和导航技术精确配合应用的思想，本文提出了格网等角航线的思想。此类航线提出的目的是使极区航线等角且在极区投影图上表现为直线，使得极区航线与极区投影、极区导航方法精确匹配，方便航行人员航行绘算和航行监控。

图3 格网导航示意图Fig.3 Diagram of grid navigation

为解决大圆航线不适用于极区航行导航的问题，定义地球椭球面上一条与所有格网航向基准线相交成固定夹角的曲线为网格等角航线。具体实现方法如下：

如图4所示，设AB为格网等角航线上的微分弧段，Aφ1,λ1为航线起点，AB与经线BC、纬线AC构成微分直角三角形ABC。格网等角航线与格网航向基准线的夹角为格网航向角为ψG，那么利用式(4)格网航向角与地理航向角的关系，可得地理航向角为ψG+λ，则∠BAC为π/2-(ψG+λ)，经线的微分弧长为RMdφ，纬线的微分弧长为RNcosφdλ，因此满足

(5)

将式(5)写成积分形式可得

(6)

对式(6)两边同时求定积分可得

(7)

式(7)就是通过已知点φ1,λ1，格网航向角为ψG的格网等角航线方程，φ,λ为航线上的任意移动点。

为验证该航线方程在极球面投影图上的投影形状，将式(7)经过式(1)和式(2)的投影变换，可得该航线在平面投影图上的方程为

(8)

由式(8)可以看出，方程式右侧为由投影基准位置和已知航线确定的已知量，因此该方程式为直线方程。验证了任意格网等角航线在极球面投影图上投影为直线。

图4 格网等角航线Fig.4 Grid rumble route

3 格网等角航线航向角和航程计算方法

3.1 格网等角航线航向角计算方法

若已知格网等角航线起点、终点的坐标φ1,λ1和φ2,λ2，可根据式(7)和两已知点坐标求解格网航向角。具体如下：

将两个坐标点分别代入式(7)，并进行化简可得

(9)

式中

特殊情况下，λ1=λ2=π/2时，ψG=π/2。此外，由式(9)可以看出，满足此式格网航向角有4个，因此需要根据两位置点坐标的关系进行格网航向角的象限判断。

3.2 格网等角航线航程计算方法

如图4所示，以dSl表示格网等角航线的微分弧长，则

(10)

由式(7)可得，格网等角航线方程中λ可以表示成φ的函数，即

λ=g(φ)

(11)

因此，航线的航程为

(12)

由于式(11)无法给出具体的解析表达式，式(12)所示航线航程需要采用数值积分的方法进行求解。

4 算例分析

为验证本文提出的格网等角航线与大圆航线、大椭圆航线的差别，进行如下航线设计仿真：已知载体从起始点(75°N，10°E)出发，分别按格网等角航线、大圆航线和大椭圆航线航行至目标点(70°N，170°E)，格网等角航线轨迹图如图5所示。格网等角航线、大椭圆航线计算采用WGS-84参考椭球模型，大圆航线计算分别采用航海学半径为6 366 707 m和极点处平均曲率半径的球体模型。利用本文推导的公式分别计算出格网等角航线的格网航向角和航程，并与大圆航线、大椭圆航线的航向和航程[24]进行比较，结果见表1与图6(1 n mile=1852 m)。

图5 格网等角航线轨迹Fig.5 Position track of grid rumble route

表1 总航程计算结果比较

图6 格网航向角计算结果比较Fig.6 Result comparison of grid direction

由表1和图6可以看出，比较格网等角航线与大圆航线，两者航程相差分别为10.47 n mile和0.21 n mile(采用不同球体半径)，格网航向角相差最大值为0.464°；比较格网等角航线与大椭圆航线，两者航程相差0.48 n mile，格网航向角相差最大值为0.471°。因此，格网等角航线和大圆航线、大椭圆航线比较相近，航程同样较短。同时，考虑到大圆航线采用球体模型与航行阶段导航设备采用的椭球体模型不一致，会存在固有原理性误差，而格网等角航线和大椭圆航线采用椭球模型，航行作业精度较高，因此格网等角航线是一种高精度的极区航线。此外，结合理论分析，格网等角航线上格网航向角处处相等且在极球面投影图上表现为直线，这种航线的特点与中低纬度地区等角航线上地理航向角处处相等且在墨卡托投影图上表现为直线相一致。因此，格网等角航线可以与输出格网航向角的格网导航技术、极球面投影精确配合，达到中低纬度地区等角航线、输出地理航向角的导航技术、墨卡托投影精确配合的相同效果，解决大圆航线、大椭圆航线与格网导航技术、极球面投影配合使用存在原理性误差的问题，便于极区航行控制和航行绘算。

5 结 论

本文在研究了极区极球面投影和格网导航方法的基础上，提出了一种极区格网等角航线，并给出了航程和格网航向角计算方法，以解决传统大圆航线与格网导航方法、极区投影图不能精确配合使用，存在原理性误差的问题。通过研究表明，格网等角航线具体航程较短、精度较高、航线上格网航向角处处相等以及在极区极球面投影图上表现为直线的优点，可以与格网导航方法、极球面投影精确配合应用，适合于极区航行。