BP神经网络和ARIMA模型的变权组合电离层TEC预报

田祥雨, 刘立龙,杨可可, 黎峻宇,陈雨田

(1.桂林理工大学 a.测绘地理信息学院;b.广西空间信息与测绘重点实验室,广西 桂林 541006;2.战路支援部队信息工程大学，郑州 450001)

电离层是全球导航定位系统的主要误差来源, 是制约定位精度的重要因素[1-2]。 目前单频接收机对TEC值进行预报主要有两种方法: 一种是采用已有的电离层模型, 如: Klobuchar模型[3]、 IRI模型、 NeQuik模型[4]， 其中应用最广泛的Klobuchar模型，只能预报电子含量的50%～60%; 另一种是基于TEC观测数据建立的预报模型, 常用的有神经网络模型、 时间序列分析法等。 BP神经网络模型具有较强的非线性处理能力, 广泛用于非线性建模、 函数逼近等方面[5]。 李淑慧等采用BP神经网络对电离层TEC提前一天预报, 结果表明，训练好的神经网络模型能够反映出不同季节的逐日变化[6]。 ARIMA模型是对非平稳时间序列建模预报的一种常见方法, 张小红等采用ARIMA模型, 分别对电离层平静期和活跃期TEC进行预报,结果表明，ARIMA模型能较好地应用于TEC预报[7]。 由于实际问题的复杂

性, 单一模型均不能综合考虑到各种因素的影响, 因此很难得到最优的预报值[8-11]。 针对此问题, 文献[12]提出变权组合预报方法, 将单一模型的预报值进行最优非负变权组合, 充分考虑不同模型在各时期预报的精度合理分配权重, 以提高预报精度。 该理论在大坝变形预报监测中得到广泛应用[13-14]。 本文利用IGS中心提供的高精度TEC数据, 分别采用BP神经网络、 ARIMA模型以及变权组合模型对不同经纬度电离层平静期和活跃期TEC进行预报, 并对预报值进行精度评定。

1 模型概述

1.1 BP神经网络模型

利用BP神经网络建模[6, 8], 将前10天的TEC值作为输入层参数, BP神经网络隐含层中的神经元使用sigmoid函数, 采用遗传算法优化来训练网络, 输出层用线性函数。 设置的输入节点数为3, 隐含层节点数为7, 输出节点数为1。 所有的数据样本都经过归一化处理。

1.2 ARIMA模型

ARIMA(p,d,q)×(P,D,Q)是一种精度较高的非线性时间序列预报方法, 且其计算简单, 操作方便。 其中， 非负整数p、d、q分别为自回归阶数、 常规差分阶数、 滑动平均阶数; 非负整数P、D、Q分别为季节性自回归阶数、 季节性常规差分阶数、 季节性移动平均阶数。 建模预报前先对非平稳时间序列进行差分,使其平稳化; 再根据时间序列样本数值的相关性,判别序列应属于何种模型, 计算其阶数并对模型中的参数进行估计; 然后对初步得到的模型进行诊断检验; 最终选择最优模型进行预报。

1.3 变权组合模型

变权组合模型的建立是先将各单一模型预报残差统计出来,按不同精度目标赋予不同的权值,使得组合预报误差平方和达到最小,即最优非负变权组合。设IGS中心提供电离层TEC序列为{Yt,t=1,2,…,n},用以上两种预报模型对其预报,预报值为Yit,它表示第i种模型在t历元的预报值,其中i=1,2;t=1,2,…,n,下同。令

(1)

(2)

设eit、et分别为第i种单一模型和变权组合模型在第t历元的TEC预报误差,则

(3)

若记Wt=[W1t,W2t]T,Et=[e1t,e2t]则

(4)

(5)

设f为最优非负变权组合预报的预报误差平方和,则最优非负变权系数的规划模式为

minf=WTEW;

(6)

(7)

其中，Rn=[1,1,…,1]T。

通过规划法可以确定变权组合模型在各历元预报值的权系数。

2 实验验证

2.1 选取数据

本文利用IGS中心提供的TEC数据,分别选取不同纬度区域电离层平静期、活跃期的TEC数据进行建模预报。实验选取2012年年积日91—105、216—230,2013年27—41和2014年60—74的低纬度(10°N、 110°E)、 中纬度(40°N、 110°E)、 高纬度(70°N、 110°E)电离层格网TEC作为平静期数据; 选取2015年年积日76—90和236—250的低纬度(10°N、 110°E)、中纬度(40°N、 110°E)、高纬度(70°N、 110°E)电离层格网TEC作为活跃期数据(表1)。

表1 IGS电离层格网数据统计Table 1 Statistics of IGS ionospheric grid data

为综合评定模型的精度,本文采用相对精度Prel(%)和均方根误差RMSE(TECu)进行各模型在电离层TEC预报中的评定[15-16]:

(8)

(9)

式中,Ipre[i]为预报的电离层TEC值;Iigs[i]为IGS发布的TEC值;n为预报时段的起始历元;m为结束历元。

2.2 实验分析

对所选数据分别用BP神经网络、 ARIMA模型和变权组合模型进行预报, 选取前10天的TEC样本数据建模, 预报后5天的TEC, 预报结果如图1～3所示。 其中IGS观测值和3种模型的预报值的对比, 以IGS观测值作为真值。 可以看出, 3种模型在平静期和活跃期均能较好地反映TEC变化特征。 在平静期，3种模型的预报值对于IGS观测值的拟合度都是中纬度最好,低纬度最差;而在活跃期，3种模型的拟合度均呈现随纬度的增加而降低的规律,即纬度越高,拟合度越低。比较相同的纬度区域，平静期的拟合度明显优于活跃期。

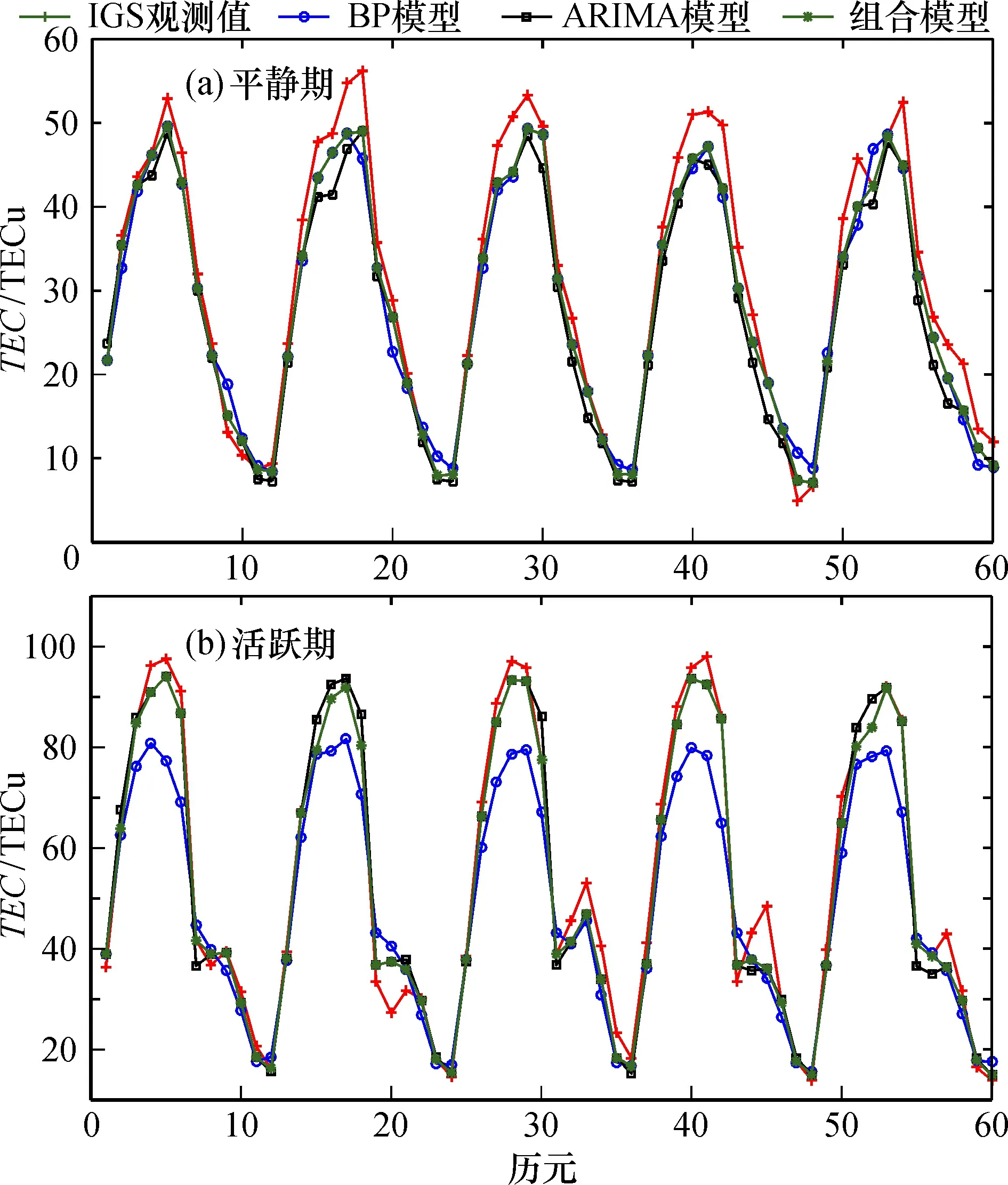
图1 低纬度地区电离层平静期(a)与活跃期(b) TEC预报结果Fig.1 TEC forecast results at low latitude of ionosphere in quiet and active periods

图2 中纬度地区电离层平静期(a)和活跃期(b) TEC值预报结果Fig.2 TEC forecast results at mid-latitude of ionosphere in quiet and active periods

图3 高纬度地区电离层平静期(a)和活跃期(b) TEC值预报结果Fig.3 TEC forecast results at high latitude of ionosphere in quiet and active periods

为了更好地比较3种模型的精度,分别统计了3种模型在电离层平静期和活跃期预报值残差分布情况。

由表2可知，在平静期，BP神经网络模型约22%的预报残差在1 TECu以内,约30%的预报残差≥3 TECu;ARIMA模型约29%的预报残差在1 TECu以内,约31%的预报残差≥ 3TECu;变权组合模型约49%的预报残差在1 TECu以内,约11%的预报数据残差≥3 TECu。由此可知,在平静期变权组合模型预报效果明显优于其他两种模型。

由表3可知,在活跃期BP神经网络模型约26%的预报残差在1 TECu以内,约31%的预报残差≥3 TECu;ARIMA模型约23%的预报残差在1 TECu以内,约32%的预报残差≥3 TECu;变权组合模型约39%的预报残差在1 TECu以内, 约22%的预报残差≥3 TECu。 由此可知, 在活跃期变权组合模型的预报效果明显优于其他两种模型。

表2 电离层平静期残差分类统计

Table 2 Residual difference of inosphere in quiet period %

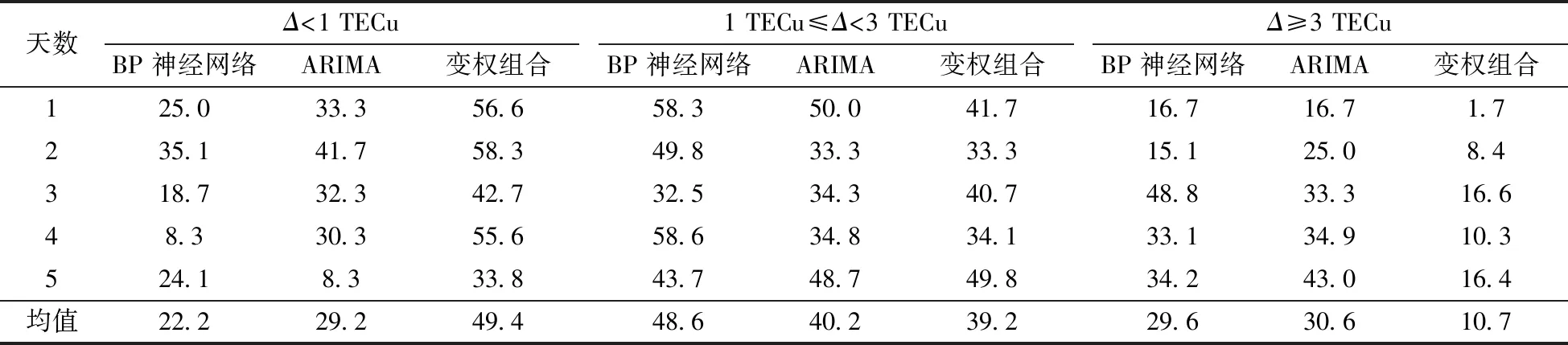
天数Δ<1 TECuBP神经网络ARIMA变权组合1 TECu≤Δ<3 TECuBP神经网络ARIMA变权组合Δ≥3 TECuBP神经网络ARIMA变权组合125.033.356.658.350.041.716.716.71.7 235.141.758.349.833.333.315.125.08.4 318.732.342.732.534.340.748.833.316.6 48.330.355.658.634.834.133.134.910.3 524.18.333.843.748.749.834.243.016.4 均值22.229.249.448.640.239.229.630.610.7

表3 电离层活跃期残差分类统计

Table 3 Residual difference of inosphere in active period %

天数Δ<1 TECuBP神经网络ARIMA变权组合1 TECu≤Δ<3 TECuBP神经网络ARIMA变权组合Δ≥3 TECuBP神经网络ARIMA变权组合138.938.866.750.055.627.811.15.65.5 216.722.227.858.352.855.625.025.016.6 336.125.044.438.947.241.725.027.813.9 422.213.927.836.133.336.141.752.836.1 516.716.726.633.336.137.950.047.235.5 均值26.123.338.743.345.039.830.631.721.5

综合可以看出，无论是平静期还是活跃期,变权组合模型预报残差平均值均小于其他两种模型,说明变权组合模型预报效果优于其他两种模型。同时,3种模型在电离层平静期的预报效果都比活跃期预报效果好。

分别统计不同纬度区域平静期、活跃期预报值的相对精度和均方根误差。

由表4可知,电离层平静期，对于BP神经网络模型,相对精度中纬度最高,低纬度最低;均方根误差中纬度最小,低纬度最大。对于ARIMA模型,相对精度中纬度最高,高纬度最低;均方根误差中纬度最小、低纬度最大。对于变权组合模型,相对精度中纬度最高,高纬度最低;均方根误差中纬度最小、低纬度最大。比较同一纬度地区,ARIMA模型预报值的相对精度和均方根误差均优于BP神经网络模型,而变权组合模型预报值的相对精度比两种单一模型都要高且均方根误差都要小。这说明,变权组合模型能够提高电离层TEC预报的精度。

由表5可知, 电离层活跃期，对于BP神经网络模型,RMSE中纬度最小, 低纬度最大; ARIMA模型,RMSE中纬度最小、低纬度最大; 变权组合模型,RMSE高纬度最小、 低纬度最大。 而相对精度3种模型则呈现统一的变化规律, 即随纬度的增大而增大。 对比来看, BP神经网络模型和ARIMA模型RMSE和相对精度各纬度区域无明显差异, 而变权组合模型的均方根误差和相对精度则明显优于各单一模型。

表4 电离层平静期预报值均方根误差和相对精度Table 4 Mean square error and relative accuracy of inospheric forecast value in quiet period

表5 电离层活跃期期预报值均方根误差和相对精度Table 5 Mean square error and relative accuracy of inospheric forecast value in active period

综合可以看出,无论电离层平静期还是活跃期,变权组合模型预报精度比其他两种单一模型都有所提高。变权组合模型根据单一模型在各历元预报精度的高低赋予不同权值,以预报误差平方和最小为准则。该模型结合了单一模型的优点,预报结果明显优于各单一模型。

为进一步说明3种模型的预报效果,统计各个模型电离层活跃期和平静期不同纬度区域的相对精度和均方根误差的平均值。

由图4可知, 3种模型平静期的相对精度明显优于活跃期的相对精度。 比较来看, 变权组合模型相对精度的均值优于ARIMA模型的均值, ARIMA模型预报相对精度的均值优于BP神经网络模型的均值。

由图5可知,3种模型的均方根误差均值在平静期和活跃期差异较大,BP神经网络模型平静期均值远大于活跃期均值,ARIMA模型平静期均值稍大于活跃期均值,而变权组合模型平静期均值小于活跃期均值。对比来看,变权组合模型的均方根误差均值优于ARIMA模型的均值,ARIMA模型的均值优于BP神经网络的均值。

综合可知,变权组合模型无论是平静期还是活跃期预报效果都有所改善。在相对精度方面，变权组合模型平静期和活跃期相对两个单一模型都要高；在均方根误差方面，变权组合模型平静期和活跃期相对两个单一模型都要小。由此可见,变权组合模型的预报效果优于两个单一模型。

图4 3种模型相对精度均值直方图Fig.4 Histogram of relative accuracy averages of three models

3 结 论

本文利用IGS中心提供的不同经纬度电离层平静期和活跃期TEC格网点数据,分别采用BP神经网络模型、ARIMA模型和变权组合模型进行短期电离层TEC预报。将预报值与IGS中心提供的观测值对比分析得出如下结论:

(1)3种模型在电离层平静期和活跃期所得预报结果均能较好地反映电离层的变化特性, 但从3种模型的预报效果来看，平静期的预报效果明显优于活跃期的预报效果。 从不同纬度区域分析, 无论是单一模型，还是变权组合模型对于中纬度的预报效果都是最优的, 且3种模型在电离层平静期和活跃期, 高纬度和低纬度的预报效果差异较大。

(2)在电离层平静期和活跃期，变权组合模型预报5 d的平均相对精度分别为94.7%和88.9%,其中预报残差小于3 TECu的比例分别达到89.3%和78.5%, 较单一模型的预报精度有显著提高。变权组合模型考虑了单一模型预报效果的不稳定性,通过改变权重提高预报的精度，比单一BP神经网络模型或ARIMA模型预报精度均有显著提高。因此利用变权组合模型短期预报电离层TEC是可行的。

由于本文采用的数据有限以及电离层时空上的不确定性,该方法对其他地区是否适用还有待验证,笔者将在未来展开进一步研究。

致谢:感谢IGS中心提供的观测数据。