商业银行系统性风险贡献度的相关性研究——基于Copu la函数的实证分析

刘志洋

（东北师范大学，吉林长春 130024）

一、引言

2007-2009年爆发的全球金融危机以及之后爆发的欧洲主权债务危机，使系统性金融风险成为学术界和金融监管当局关注的重点。鉴于金融风险监管存在疏漏，各国金融监管当局纷纷出台相关监管法案，比如《巴塞尔协议III》要求对系统重要性金融机构施加更为严格的监管，Dodd-Frank法案也提出了类似的监管要求。2017年全国金融工作会议将系统性风险管理放在重要位置，同年十九大报告中也指出“健全货币政策和宏观审慎政策双支柱调控框架”、“守住不发生系统性金融风险的底线”，因此对我国系统性金融风险进行测算十分重要。在中国金融体系中，商业银行居于主体地位，而其中又以国有商业银行和全国性股份制商业银行为主。任何一家主要商业银行风险的增加都有可能加剧系统性风险，因此在研究系统性风险贡献度的同时，还应进一步研究该指标的相关性，即一家商业银行系统性风险贡献度的上升是否会导致其他商业银行系统性风险贡献度的上升。基于此考虑，本文在测度我国上市商业银行系统性风险贡献度的基础上，研究各上市商业银行系统性风险贡献度之间的相关性，以期为降低系统性金融风险，实施宏观审慎监管提供参考。

二、文献综述

金融危机期间，一家金融机构陷入困境往往会通过金融市场传染给其他经营稳健的金融机构，而这种风险传染特征很多情况下无法用正常的理论来解释。Bertero and Mayer（1990）发现1987年美国股灾爆发时，全球股票市场相关性显著增加。Forbes and Rigobon（2002）研究1987年美国股灾、墨西哥金融危机和东南亚金融危机，发现在考虑了股票市场异质性后，各国股票市场价格不存在相关性。2008年次贷危机爆发后，学者们提出大量有关测度系统性金融风险的指标。Bisias et al.（2012）在对系统性金融风险测度指标进行总结后指出，没有任何一个指标能够准确预测金融危机，同时Danielsson et al.（2016）也质疑系统性风险测度指标的预测能力。为了解决模型预测偏差问题，Giglio et al.（2016）将各种系统性金融风险的测度指标汇总成单一指标，有效运用了所有相关信息对系统性风险进行预测。在所有系统性风险测度指标中，Adrian and Brunnermeier（2016）提出的ΔCoVaR是最常用的指标之一。之后许多学者研究了金融系统陷入困境对单家金融机构的影响，这类研究主要使用结构模型或简约模型进行分析，代表性文献有Lehar（2005）和Brownlees and Engle（2017）。

在系统性风险贡献度研究方面，学术界普遍认为规模越大的商业银行系统性风险贡献度越高，代表性文献包括Huang et al.（2009）、Zhang et al.（2015）、Laeven et al.（2016）等，但Weiβ et al.（2014）认为规模因素不一定能够永久决定一家金融机构系统性风险贡献度，且大型商业银行之间不一定有传染风险。同时，大量研究表明金融机构间关联程度是决定系统性风险高低的主要原因之一，相关研究包括López-Espinosa et al.（2013），Hautsch et al.（2015）和Betz et al.（2016）。

使用股票市场数据研究系统性风险的结构化模型是2008年次贷危机爆发后学者们使用的主要研究方法之一。Brownlees and Engle（2017）将金融危机定义为股票市场指数收益率在6个月内下跌40%。然而此定义有一定缺陷，比如2000年网络股泡沫破灭时，股票指数收益率从最高点跌至最低点，跌幅达50%。因此，Varotto and Zhao（2018）认为Brownlees and Engle（2017）对金融危机的定义具有“系统（Systematic）”特征，但不具备“系统性（Systemic）”特征，而结构化模型具有“系统性（Systemic）”特征。

根据资产组合理论，系统性金融风险的上升往往伴随着金融机构传染风险的增加。大量学者使用极值理论、马尔科夫状态转移模型等工具测量风险传染。然而马尔科夫状态转移模型在多元正态分布以及非线性相关性处理上存在缺陷，而极值理论由于假设存在渐进相关性而高估金融风险。Copula函数的优势在于能够包含两个随机变量相关性的所有信息，且能够处理非线性问题。另外，Copula函数也包含了随机变量的尾部相关信息，这恰恰是传染风险主要关注点之一。本文在现有文献研究基础上，以上市商业银行为研究样本，测度我国商业银行系统性风险贡献度，并使用Copula函数研究系统性风险贡献度之间的相关性，以期为风险监管提供参考。

三、研究方法

（一）系统性风险贡献度测度指标

本文使用基于市值加权的银行业指数代表商业银行系统性风险状况，并使用GARCH-DCC模型求解系统性风险测度过程中涉及的相关系数和变量的标准差。

1.ΔCoVaR

Adrian and Brunnermeier（2016）将CoVaR定义为单家商业银行陷入困境后，商业银行系统整体的VaR值；ΔCoVaRi定义为当商业银行i陷入困境后，银行系统VaR值与商业银行i正常经营时银行系统VaR值的差。根据Acharya et al.（2012）的研究成果，本文假设商业银行i股票收益率和银行业指数收益率的期望值为0。在正态分布假设下，商业银行i的ΔCoVaR表达式为：

其中，σmt为银行业指数收益率的标准差，ρimt为商业银行i与银行业指数的相关系数，N-1（q）表示正态分布在q分位点的值。本文q的取值为0.01。

2.MES

参考Acharya et al.（2010）的研究成果，MES的含义是银行系统陷入困境对单家商业银行的影响，表达式为：

其中rit表示商业银行i的股票收益率，rmt表示银行业指数收益率，c为刻画银行系统陷入压力情景的变量。本文假设c的取值为-0.05。参考Kreis and Leisen（2017）的研究成果，假设rit和rmt的期望值为0。在正态分布假设下，商业银行i的MES表达式为：

3.CES

参考Banulescu and Dumitrescu（2015）的研究成果，CES的含义是商业银行i对银行系统尾部期望损失的贡献度，表达式为：

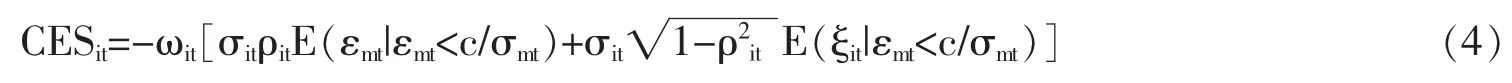
其中，ωit表示t时刻商业银行i的市值占银行系统整体市值的权重，εmt和ξit为GARCH-DCC模型估计后生成的残差项。c为刻画银行系统陷入压力情景的变量，本文c取值为-0.05。

（二）基于Copula函数的相关性测度

Copula函数的优势是可以刻画变量之间的相关结构，其优势包括：第一，对随机变量的单调变换不改变Copula函数；第二，Copula函数与Kendall和Spearman相关系数具有一致性；第三，Copula函数能够刻画随机变量之间的尾部相关性，进而能够研究风险传染。在多元分布中，Copula函数可以将每一个边缘分布连接起来，从而得到多元分布函数。假设D为n维分布函数，每个维度的边缘概率密度为F1，F2，……，Fn，则对于n维空间中所有x，Copula函数C定义为：

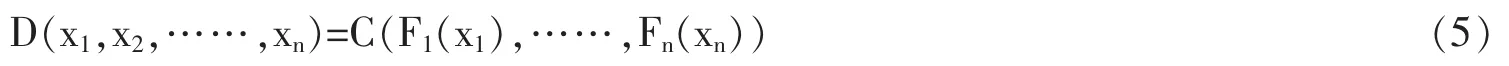
如果F1，F2，……，Fn连续，则C唯一。如果C是n维Copula函数，F1，F2，……，Fn为边缘分布函数，则D为相应的多元分布函数。如果D是连续多元分布函数，则可以将边缘分布函数与多元分布函数分开，二者可以通过Copula函数相连，进而表现出数据的相关结构。假设Fi可微，C和D为n次可微，则D的密度函数为：

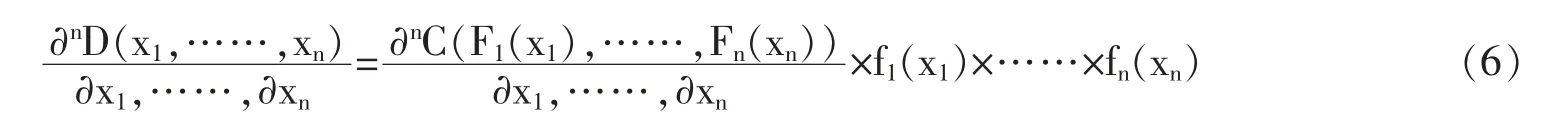
从式（6）可以看出，Copula函数刻画了变量之间的相关结构。

1.上尾相关性

为研究商业银行风险传染，本文需要测度商业银行同时出现某种情况的可能性。令X和Y为连续随机变量，其边缘分布函数为F和G。令u=F（X），v=G（Y），则根据Copula函数理论，X和Y的上尾相关性（Upper Tail Dependence）为：

上尾相关性关注一家商业银行系统性风险贡献度的降低与另外一家商业银行系统性风险贡献度降低之间的关系。本文使用Gumbel Copula函数刻画商业银行系统性风险贡献度的上尾相关性。

2.下尾相关性

在系统性风险研究中，监管当局更加关注的是下尾相关性，即一家商业银行系统性风险贡献度的上升与另外一家商业银行系统性风险贡献度上升之间的关系。随机变量X和Y的下尾相关性（Down Tail Dependence）为：

本文使用Clayton Copula函数刻画商业银行系统性风险贡献度的下尾相关性。

3.Kendall相关系数

如果存在两个随机变量（X1，X2）和（Y1，Y2），P［（X1-Y1）（X2-Y2）＞0］-P［（X1-Y1）（X2-Y2）＜0］＞0说明X和Y变化方向趋于一致。Kendall相关系数τ 定义为：

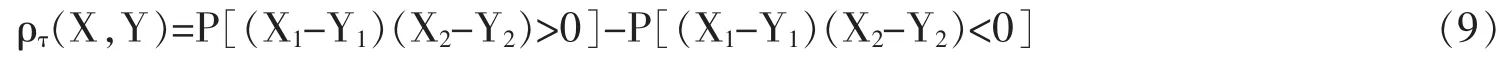
根据Copula函数理论，Kendall相关系数τ 可以写成：

Kendall相关系数τ 可以用来研究随机变量之间的非线性相关性。本文分别对Gumbel Copula和Clayton Copula计算Kendall相关系数τ。此外，为了研究金融系统正常时期各个商业银行系统性风险贡献度之间的相关性，使用Frank Copula函数测度表示正常时期商业银行系统性风险贡献度相关性的Kendall相关系数τ。

四、样本选取与实证分析

（一）样本选取

本文研究对象为2007年1月至2017年12月，我国上市商业银行股票收益率周数据，数据来源为Wind数据库。由于许多城市商业银行在2017年上市，而本文计算系统性风险贡献度需要大样本，因此选取2016年之前上市的16家商业银行。16家商业银行包括5家国有大型商业银行（工商银行、农业银行、中国银行、建设银行、交通银行）、8家全国性股份制商业银行（中信银行、光大银行、浦东发展银行、招商银行、平安银行、兴业银行、民生银行、华夏银行）和3家城市商业银行（宁波银行、南京银行、北京银行）。

（二）实证分析

本文在测度样本商业银行3类系统性风险贡献度指标（ΔCoVaR、MES和CES）之后，使用Copula函数测度各家样本商业银行系统性风险贡献度之间的尾部相关性以及Kendall秩相关系数。

1.系统性风险贡献度测度结果

从式（1）、式（3）和式（4）可以看出，ΔCoVaR和CES关注单家商业银行对银行系统的影响，而MES关注的则是银行系统陷入困境对单家商业银行的影响。由于式（1）假设随机变量服从正态分布，因此式（1）更加关注金融系统正常状态下的系统性风险贡献度，而式（4）更加关注的是单家商业银行在银行系统处于极端状态下的风险贡献度。图1至图3分别为商业银行系统性风险贡献度统计指标走势图。从图1可以看出，各上市商业银行ΔCoVaR值的走势基本一致。2008年金融危机期间以及2014-2015年均为最低，说明当时我国商业银行系统性风险较高，各家上市商业银行对银行业系统性风险的贡献度均较大。

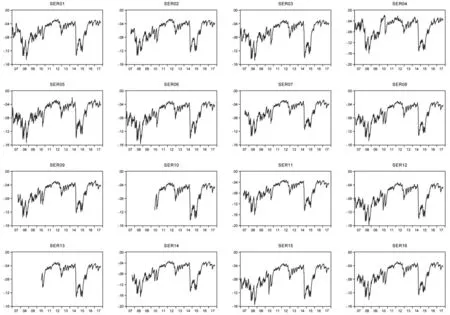
图1 样本商业银行ΔCoVaR走势图

从CES指标来看（如图2所示），样本商业银行极端风险贡献度的走势并不一致，且波动性较强。从股份制商业银行来看，平安银行、浦发银行、华夏银行、兴业银行、民生银行、中信银行和光大银行在2013年前后系统性风险贡献度较高；招商银行在2016-2017年系统性风险贡献度较高。从城市商业银行来看，CES整体波动性较强，且在2016-2017年显著上升。从国有大型商业银行来看，5家商业银行系统性风险贡献度走势并不一致。整体来看，股份制商业银行的系统性风险贡献度具有一致性，但城市商业银行和国有大型商业银行风险贡献程度各具特点。

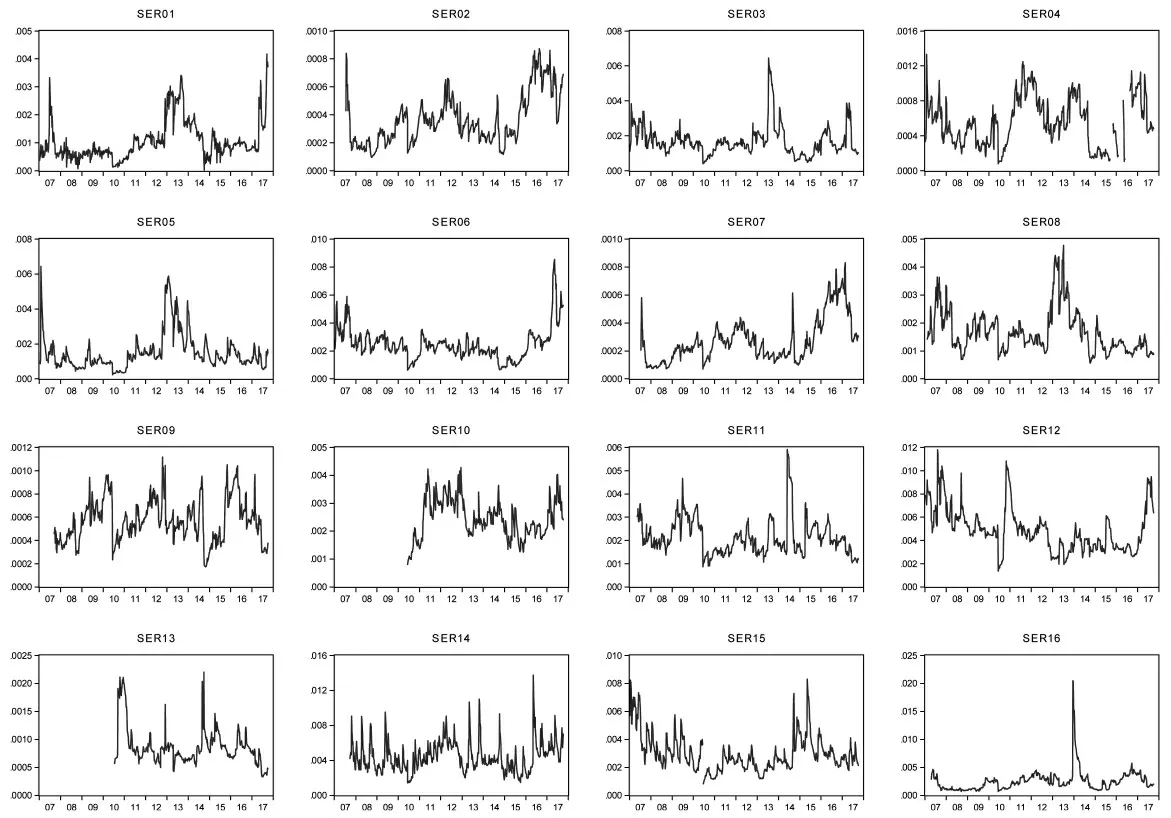
图2 样本商业银行CES走势图

从MES指标来看（如图3所示），金融系统陷入困境对各家商业银行的影响模式基本一致，呈现出分时段波动聚集现象。在2008年金融危机期间、2012-2013年和2014-2015年三个时间段，银行系统性风险的增加对每家商业银行的影响都非常大。

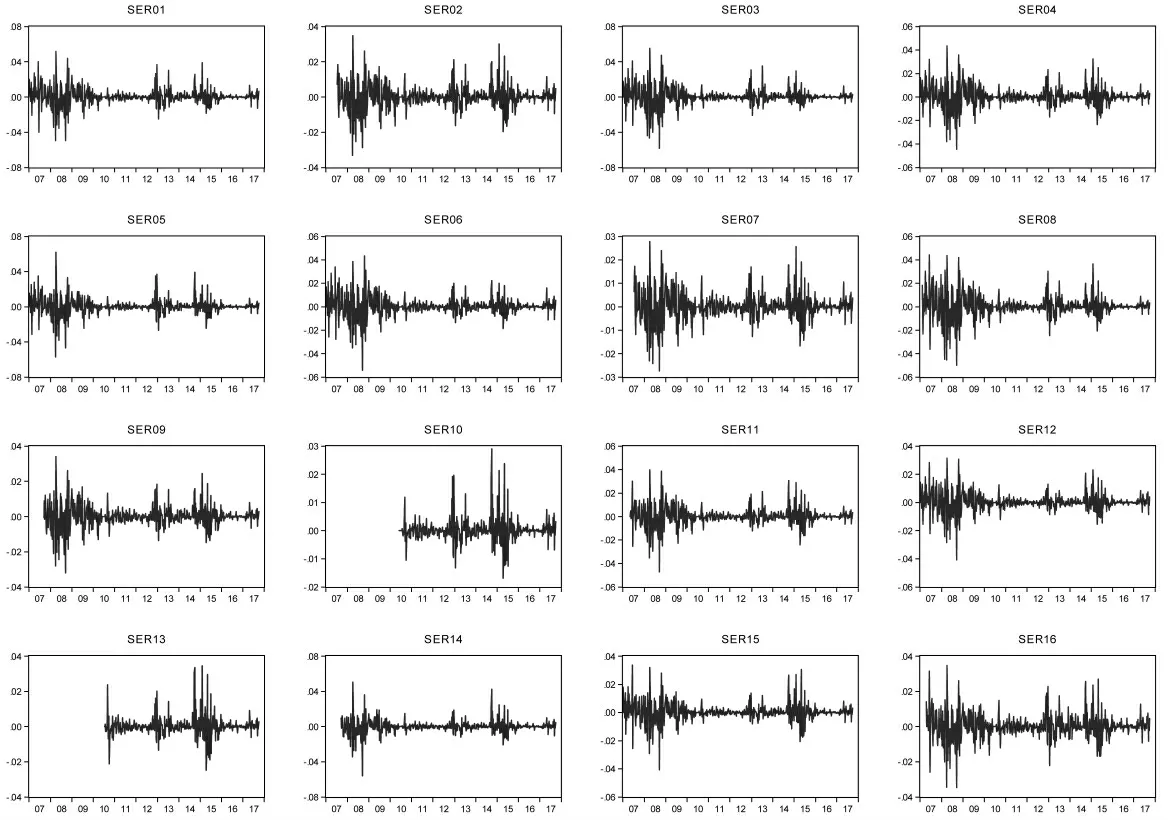
图3 样本商业银行MES走势图

2.系统性风险贡献度相关性分析

本文使用Clayton Copula函数、Gumbel Copula函数和Frank Copula函数测度商业银行系统性风险贡献度之间的秩相关系数，同时使用Clayton Copula函数和Gumbel Copula函数测度商业银行系统性风险贡献度之间的下尾相关系数和上尾相关系数。在此基础上，分别计算商业银行系统性风险贡献度与其他商业银行系统性风险贡献度之间相关系数的平均值，用于表示单家商业银行与银行系统关联性情况。

表1为各家上市商业银行MES相关系数平均值。从表1可以看出，各商业银行MES相关性都非常高，这与图3显示的样本商业银行MES走势互为印证。从下尾相关系数来看，除农业银行和光大银行外，各商业银行相关系数平均值均在0.9以上，说明一旦金融系统陷入困境，样本商业银行风险都会增加。农业银行和光大银行与其他商业银行Clayton下尾相关系数的平均值分别为0.8976和0.8940，说明农业银行和光大银行在金融系统陷入困境后，股票收益率跌幅较轻。Gumbel上尾相关系数也显示，金融系统繁荣时期，农业银行和光大银行股票收益率的涨幅低于其他商业银行。从Clayton Copula函数的秩相关系数来看，农业银行和光大银行最低，说明两家银行受银行系统性风险的影响程度最低。国有大型商业银行与股份制商业银行、城市商业银行的平均相关系数基本一致，说明规模因素不一定是系统性风险贡献度高低的主要决定因素（陈忠阳和刘志洋，2013；刘志洋，2015）。

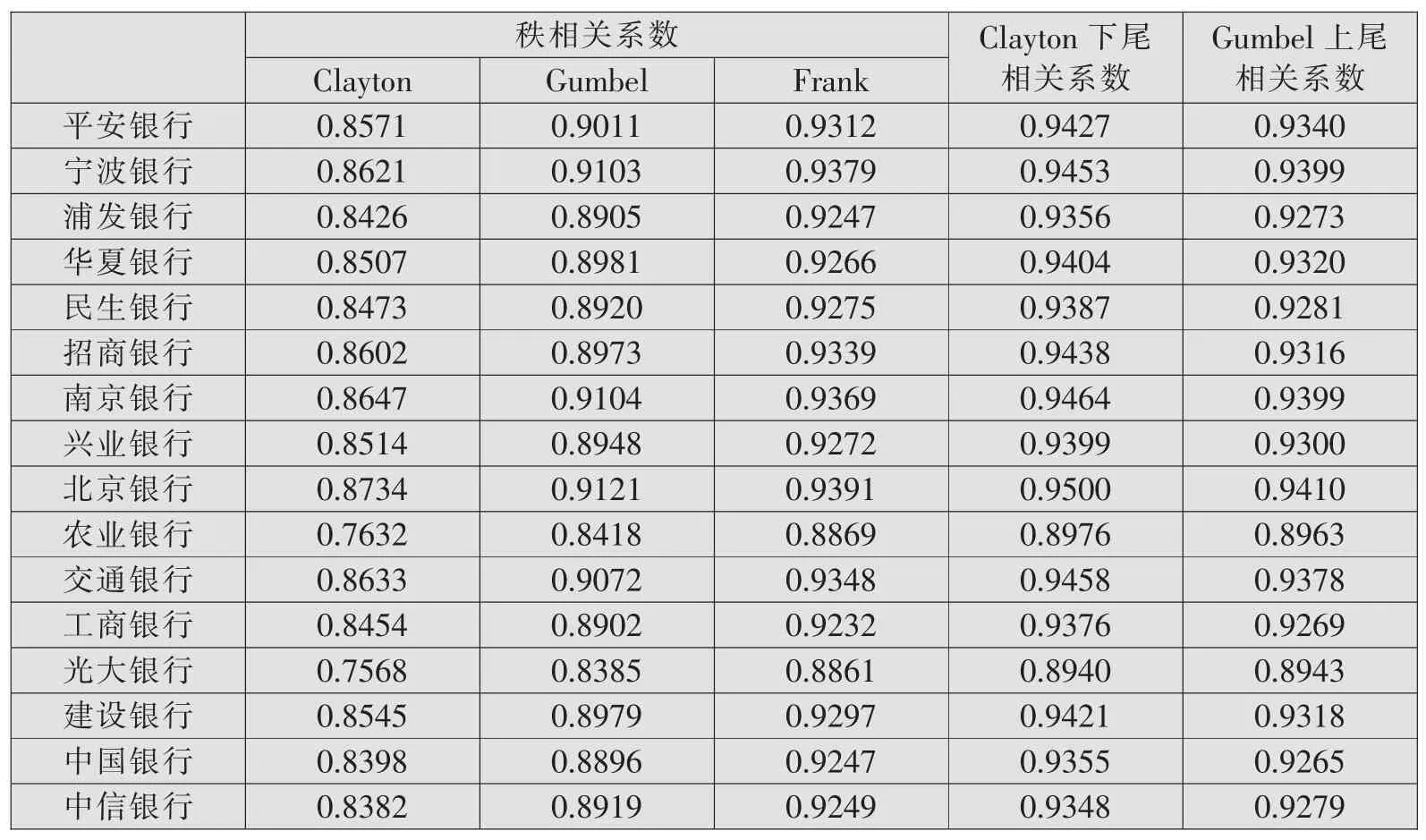
表1 系统性风险贡献度的相关系数（MES）

表2为各家上市商业银行CES相关系数平均值。可以看出，各上市商业银行CES的平均相关系数绝对值要显著低于MES平均相关系数绝对值，说明商业银行对银行系统极端风险的风险贡献度相关性较低，最高在0.3左右，但银行系统繁荣期风险贡献度的平均相关系数较高，均在0.5以上。从Clayton下尾相关系数来看，工商银行、光大银行和中国银行对银行系统极端风险贡献度的平均相关系数较低，无论是Clayton下尾相关系数，还是秩相关系数，均在0.1以下，说明一旦工商银行、中国银行和光大银行陷入困境，其对银行系统的负面冲击小于其他商业银行。需要注意的是，3家商业银行Frank Copula函数的秩相关系数为负值，说明金融系统正常时期，3家商业银行对稳定银行系统能发挥重要作用。同样，国有大型商业银行与其他商业银行相关系数平均值并不显著高于股份制商业银行和城市商业银行。

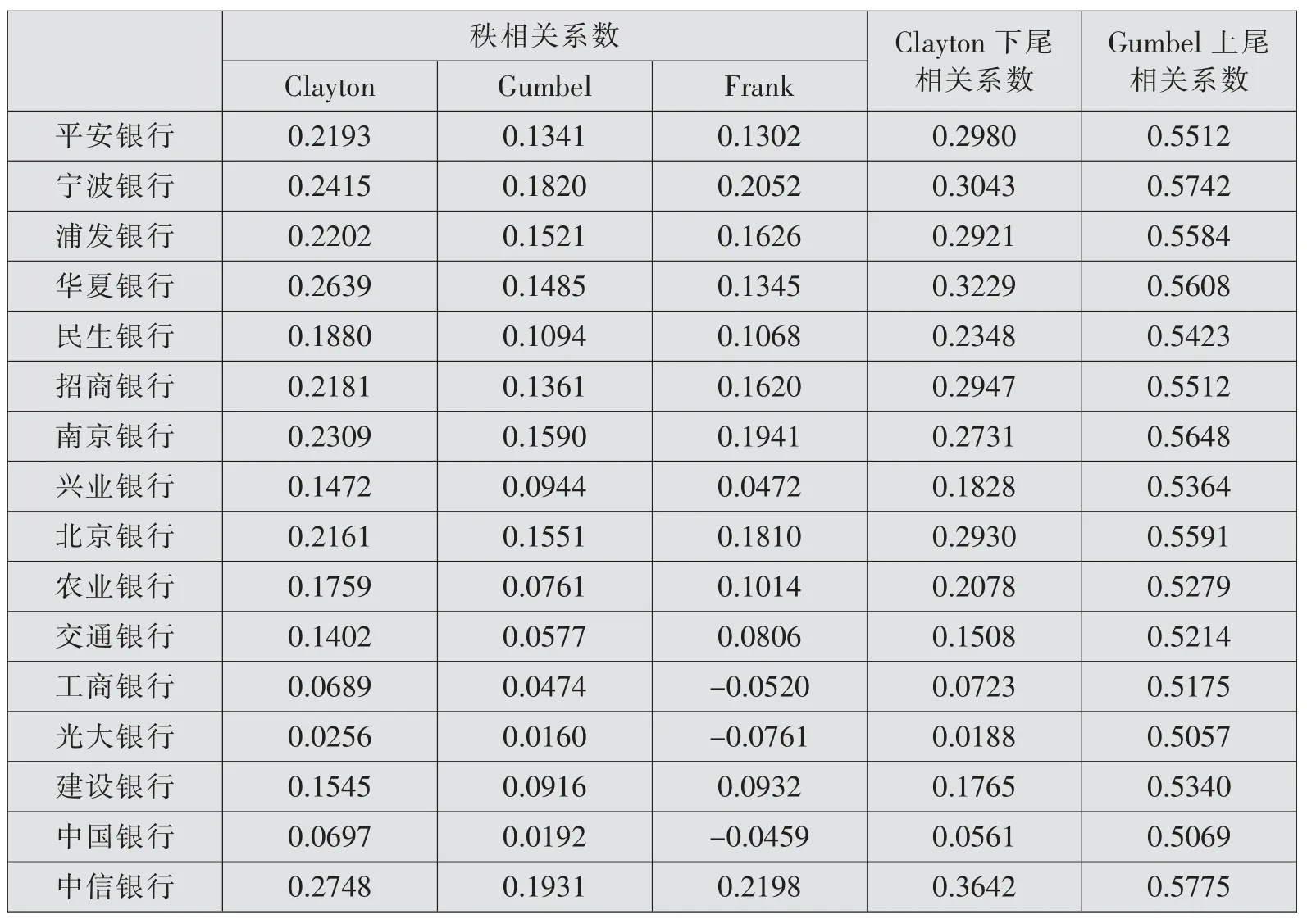
表2 系统性风险贡献度的相关系数（CES）

表3为各家上市商业银行ΔCoVaR相关系数平均值。可以看出，ΔCoVaR的相关性绝对值要显著高于CES相关性绝对值，与MES几乎相当，说明在正常时期，各商业银行系统性风险贡献度相关性较高，各类型商业银行相关系数的平均值在0.8～0.9。从Clayton下尾相关系数来看，华夏银行、光大银行和农业银行的系统性风险贡献度相关性相对较低，同时Clayton Copula秩相关系数也显示类似结果，说明3家商业银行系统性风险贡献度小于其他商业银行。同样，国有大型商业银行与其他商业银行相关系数的平均值并没有显著高于股份制商业银行和城市商业银行。

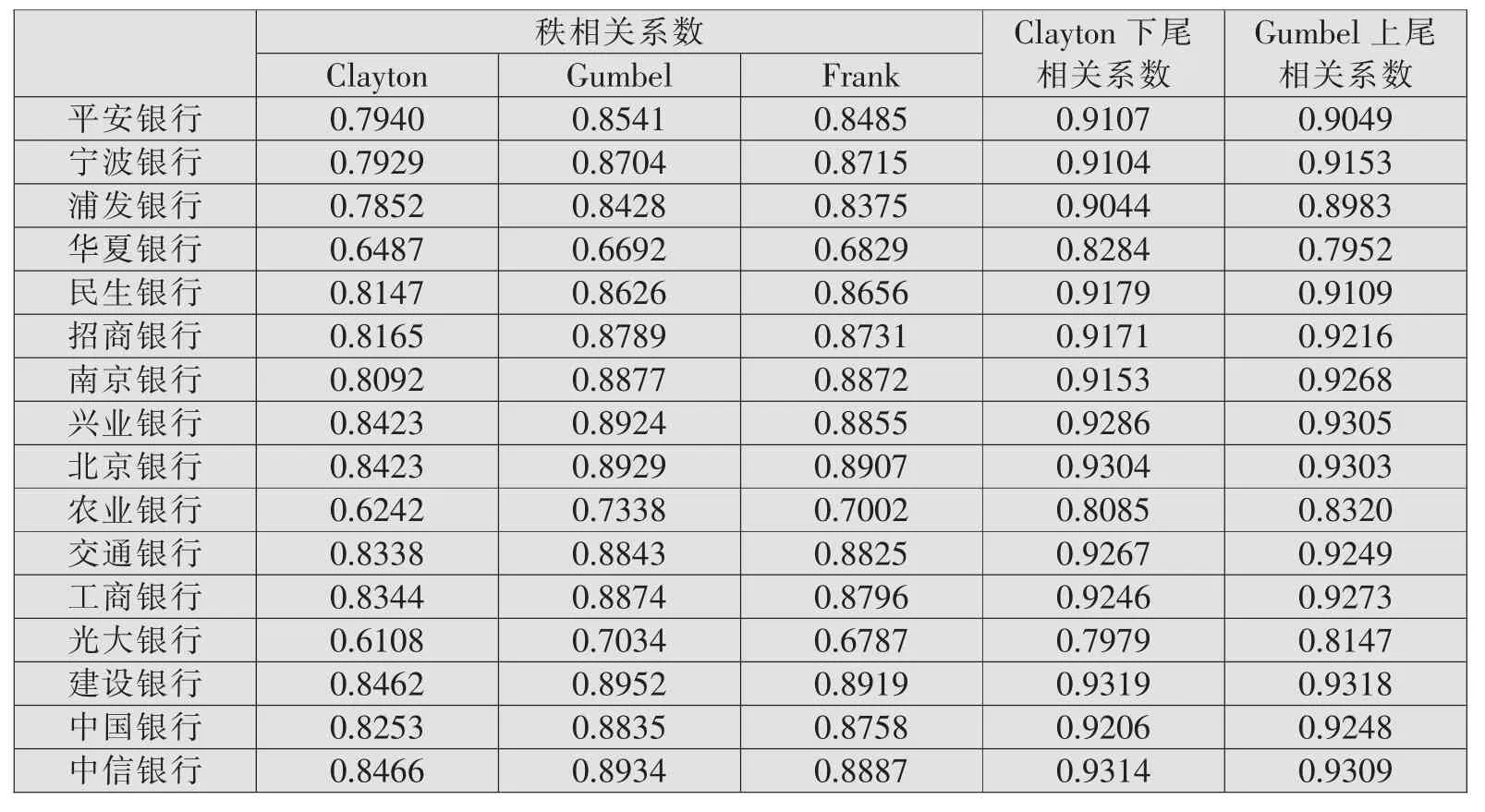
表3 系统性风险贡献度的相关系数（ΔCoVaR）

五、结论

2008年金融危机爆发后，测度系统性风险与金融机构系统性风险贡献度成为学术界主要研究方向之一。对于中国上市商业银行来说，对商业银行系统性风险贡献度的研究相对丰富，但对商业银行系统性风险贡献度相关性的研究并不多见。本文在测度了各家上市商业银行ΔCoVaR、MES和CES基础上，使用Copula函数分析了商业银行间系统性风险贡献度的相关性。商业银行系统性风险贡献度相关性较高意味着一家商业银行系统性风险贡献度的增加会导致其他商业银行系统性风险贡献度的增加，进而增加银行系统性风险。实证分析表明，中国上市商业银行系统性风险贡献度的平均相关系数非常高，说明单家商业银行系统性风险贡献度的上升会导致银行系统性风险的增加。

同时，实证分析结果表明各个商业银行MES的平均相关系数较高，说明银行系统陷入困境对单家商业银行的影响非常大，但对农业银行和光大银行的影响相对较低。在CES方面，工商银行、中国银行和光大银行极端风险贡献度的增加对其他商业银行极端风险贡献度的影响较弱。在ΔCoVaR方面，华夏银行、光大银行和农业银行正常状态下系统性风险贡献度的增加对其他商业银行系统性风险贡献度的影响相对较弱。同时，国有大型商业银行相关系数的平均值并没有显著高于股份制商业银行和城市商业银行。总体上，本文认为对于系统性金融风险的监管，不能仅仅关注系统性风险贡献度，还要关注各商业银行间系统性风险贡献度的相关性，进而制定系统重要性金融机构管理框架。