香港沿岸台风暴潮灾害联合强度概率分析

陈 磊

(浙江大学舟山海洋研究中心, 浙江 舟山 316021)

1 研究背景

中国香港地区位于台风频发的西北太平洋沿岸，每年都有热带气旋影响或者登陆，这也是沿岸居民和生态环境所面临的最不利的自然灾害风险[1]。台风经过香港时，它在不同的沿岸地区引发的风暴潮增水过程有所不同，对当地的破坏程度也有较大差异。选择台风过程引发的最大台风暴潮增水作为研究对象，它可以在一定程度上反映该风暴潮过程对该验潮站附近海域的影响。通过对香港多个验潮站观测得到的台风暴潮最大增水数据进行联合概率分析，能够综合评估该台风暴潮过程对香港地区的整体影响。

对不同验潮站的风暴增水进行联合概率分析，需要通过一些方法获得联合概率分布。目前最常用的是Copula函数构造法[2-5]。Copula函数是一种多元性质的函数，通过引入参数描述不同变量间的相关性。实际上Copula函数是通过联合分布函数将它们各自的边缘分布函数结合在一起的函数，因此也可称之为连接函数。Copula函数已经广泛应用于陆地水文[6-7]、金融[8]、风险管理[9]、生物学[10]等多个领域。近年来Copula函数也被广泛引进到海洋水文研究中。陈子燊等[11]、陈玲舫等[12]利用4类常用的二维Archimedean Copula函数，分别建立了粤东汕头海域年最大增水与相应风速、海口年最大增水与相应日期最大风速的联合概率分布。Dong等[13]基于Copula和二元复合极值分布，建立了珠江口天文潮和增水的联合概率分布，并对其联合重现频率进行了分析。Rueda等[14]针对风暴过程引发的极值波高和风暴增水，利用广义极值分布边缘和Gaussian Copula函数，构造了二者的联合概率模型，用以描述风暴的强度。

本文选择香港东部沿岸的两个验潮站——鲗鱼涌和大埔滘，基于1999-2018年间影响香港的台风过程所引发的最大风暴增水数据，利用广义极值分布和二元Copula函数，建立鲗鱼涌和大埔滘两地最大风暴增水的联合概率分布，对台风引发的香港东部风暴潮灾害强度进行综合评估。

2 风暴增水的概率模型

一场台风经过某地区时，会引发附近各海域潮位不同程度的增加[15]。不同验潮站会测得台风过程中该站的最大风暴增水，统计一定期间的长周期序列，可以进行风暴增水概率分布的拟合。对两个验潮站进行联合重现概率分析时，需要构建合适的联合概率模型。

2.1 边缘概率分布

相较于皮尔逊Ⅲ型分布，广义极值(GEV)分布属于理论上的极值分布，更为适用于台风过程引发的最大增水数据。因此，本文选用GEV分布作为边缘分布，对台风过程中某验潮站的最大风暴增水(设为随机变量X)进行拟合。GEVl分布的累积概率分布函数为：

F(x)=exp{-[1+ξ((x-μ)/σ)]-1/ξ},

1+ξ(x-μ)/σ>0

(1)

式中：μ为位置参数；σ为尺度参数；ξ为形状参数。本文选用极大似然法进行参数估计。

2.2 二元Copula函数

Copula函数的概念是由Sklar提出，二元Copula函数结构简单，而两种事物的相关性又便于寻找规律。二元Copula函数C(u,v)是从[0, 1]2→[0, 1]的映射。

本文选用二元Gumbel-Hougaard Copula函数来构造联合概率分布。其分布函数C(u,v)结构形式为：

(2)

式中：θ为相关参数，且θ≥ 1，其与Kendall秩相关系数τ有个固定的相关关系。具体关系为τ=1-1/θ。当θ→ +∞时，U与V趋于完全相关；当θ=1时，U与V独立。

2.3 风暴增水最大值的联合概率分布

Sklar定理是所有Copula理论的基石，通过Sklar定理可以完成多个边缘分布向联合分布的转换。其内容如下：

假若FXY(x,y)是关于随机变量X和Y的二维联合分布函数，随机变量X和Y的边缘分布函数分别为FX(x)和FY(y)，根据Sklar定理则必然存在一个二元Copula函数C(u,v)满足对任意的(x,y) ∈[-∞, +∞]2，则有：

FXY(x,y)=C(u,v)=C(FX(x),FY(y))

(3)

若FX(x)与FY(y)连续，则C(u,v)是唯一的，否则C(u,v)由RanFX×RanFY唯一确定(Ran表示值域)。反之，如果C(u,v)为二元Copula函数，FX(x)和FY(y) 分别为X和Y为边缘分布函数，则由公式(3)确定的函数F(x,y)即为变量X和Y的二维联合分布函数。

对于两验潮站的台风过程中，最大风暴增水分别用随机变量X和Y表示，X和Y的边缘分布服从GEV分布，选用二元Gumbel-Hougaard Copula作为连接函数。则根据Sklar定理和公式(3)，可得到同一台风过程中两验潮站的最大风暴增水的联合概率分布FXY(x,y)。其中：

FX(x)=exp{-[1+ξX((x-μX)/σX)]-1/ξX}

(4)

FY(y)=exp{-[1+ξY((y-μY)/σY)]-1/ξY}

(5)

式中：σX和σY分别为X和Y的尺度参数；ξX和ξY分别为X和Y的形状参数；μX和μY分别为GEV分布中X和Y的位置参数。

2.4 风暴联合强度

这里应用两验潮站的风暴增水联合重现频次作为其强度的表征。设某台风过程经过时，引发两验潮站的最大风暴增水分别为x0和y0，则风暴增水联合重现频次T(x0,y0)的定义为：

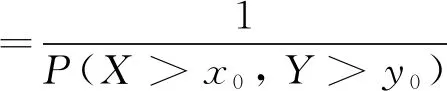
(6)

式中：FX(x)和FY(y)分别为X和Y对应的边缘分布函数，服从相应的Gumbel分布，FXY(x,y)为联合概率分布。

3 实例分析

本文选用1999-2018年香港东部鲗鱼涌和大埔滘两个验潮站的风暴增水数据，每场台风过程引发的这两站的最大风暴增水序对见图1。从图1中可看出，二者存在较强的线性相关性，且存在一特大值(2018年9月超强台风山竹所致)。鲗鱼涌验潮站和大埔滘验潮站分别位于香港东岸的南北两侧，可以在一定程度上代表台风暴潮对香港东部的影响。

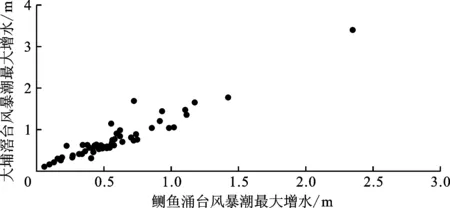
图1 1999-2018年鲗鱼涌和大埔滘台风暴潮最大增水序对

3.1 边缘分布拟合

利用公式(4)和(5)的GEV分布，分别对鲗鱼涌和大埔滘两个验潮站的台风暴潮最大增水序列进行拟合。参数估计和拟合结果见表1和图2。

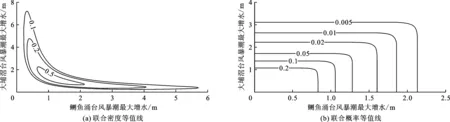
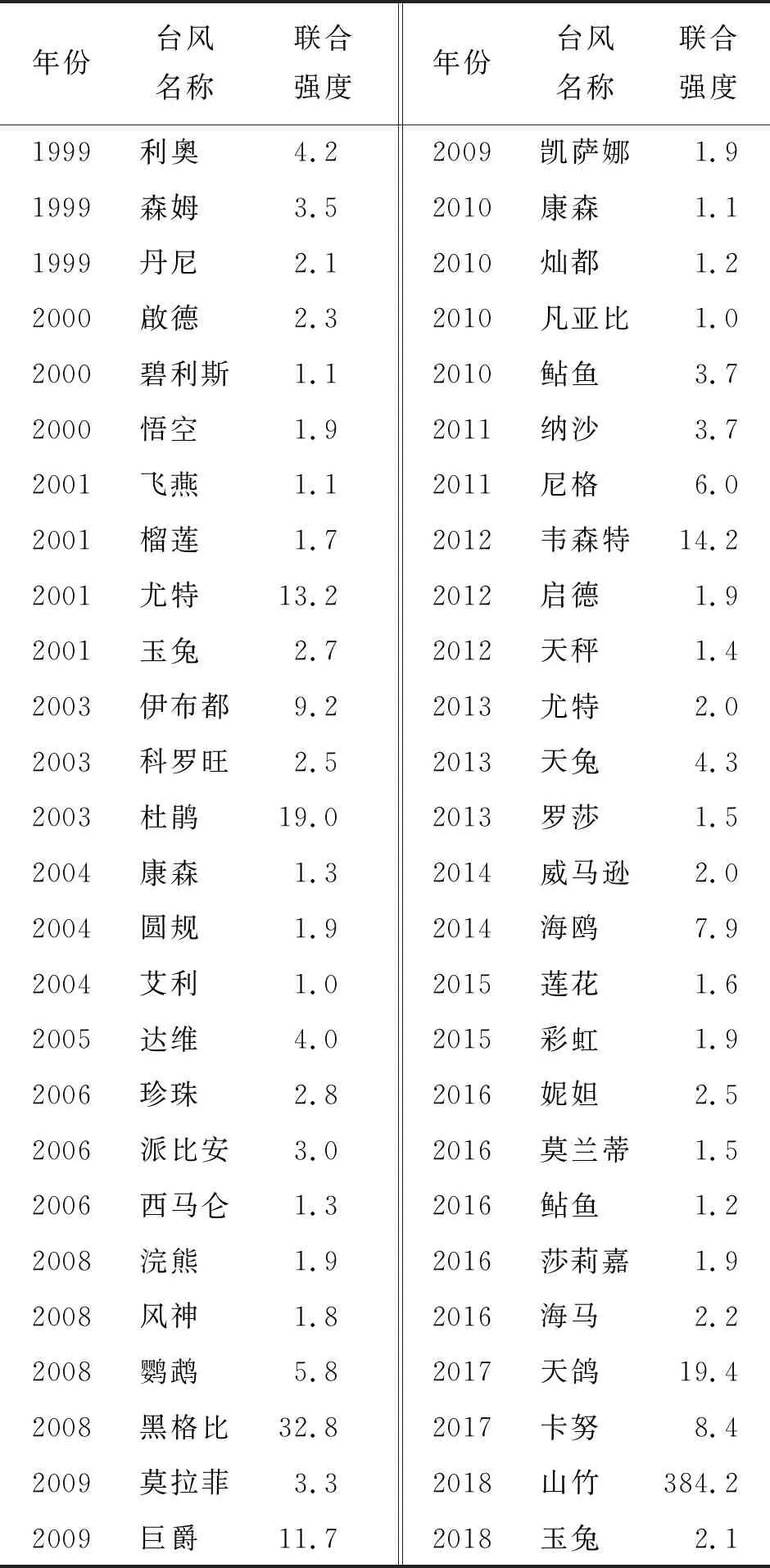
结果显示，GEV分布对两个序列的拟合优度较好，平均离差平方和均较小，且在置信度为0.05的条件下，均通过了K-S检验(Dn

3.2 联合强度分析

获得边缘GEV分布的拟合结果后，根据Sklar定理和公式(3)，利用Gumbel-Hougaard Copula，得到鲗鱼涌和大埔滘两验潮站的台风过程最大风暴增水的联合概率分布FXY(x,y)。

对建立的二元概率分布进行拟合优度检验，包括χ2检验和K-S检验(见表2)。结果表明，采用Gumbel-Hougaard Copula获得的二元模型拟合良好，在置信度为0.05的条件下，通过了这两种检验。图3(a)、3(b)分别为联合密度等值线和联合概率等值线。

表1 鲗鱼涌站和大埔滘站台风暴潮最大增水序列的参数估计及GEV分布拟合

图2 鲗鱼涌和大埔滘台风暴潮最大增水GEV分布拟合

表2 鲗鱼涌站和大埔滘站台风暴潮最大增水的拟合优度检验结果

图3 鲗鱼涌和大埔滘台风暴潮最大增水的联合密度和联合概率等值线

通过公式(6)，可以计算鲗鱼涌和大埔滘两验潮站的风暴增水联合重现频次T(x0,y0)。结果见表3，给出的联合重现频次值可作为台风暴潮的联合强度。

表3 1999-2018年鲗鱼涌站和大埔滘站台风暴潮最大增水的联合强度

由表3可知，2018年9月的超强台风山竹所引发的风暴潮强度最大，其联合重现频次达到了384.2，这与实际情况相符。2000年8月的台风悟空在鲗鱼涌站和大埔滘站所引发的最大风暴增水分别为0.49、0.55 m；2008年的台风浣熊在这两站引发的最大风暴增水分别为0.38、0.62 m，但其联合重现频次均为1.9。同样类似的情况如1999年4月的台风利奥与2013年的超强台风天兔等。这说明综合考虑两验潮站的数据，可以综合评估台风暴潮对香港东部沿岸的影响。

4 结 论

本文基于1999-2018年香港东部鲗鱼涌和大埔滘两个验潮站的台风暴潮增水数据，对香港东部沿岸的台风暴潮强度进行了联合概率评估，并得出如下结论。

(1)鲗鱼涌和大埔滘两验潮站在台风过程中的最大风暴增水序列分别采用GEV分布拟合，结果优良。GEV分布适合这两个验潮站。

(2)以GEV分布作为边缘分布，采用Gumbel-Hougaard Copula构造的二元联合概率分布，适合鲗鱼涌和大埔滘两站的最大风暴增水数据对，拟合良好。Gumbel-Hougaard Copula构造的二元联合概率分布函数具体的构造过程和使用方法可以推广到其他类似事例当中。

(3)基于两站最大风暴增水变量的联合重现频次，能够反映台风在香港东部引发的风暴潮的强度，这种联合概率分析较一元分析有更强的地区适用性，因为事物本身是有相关性的，这种联合在一起综合考虑也更有其合理性。