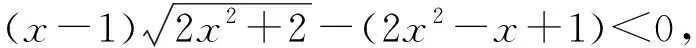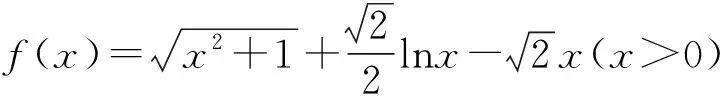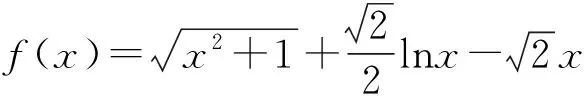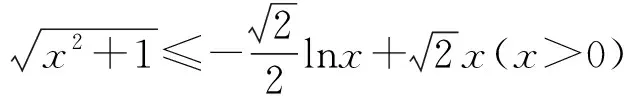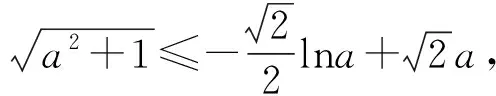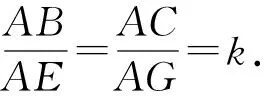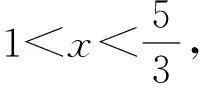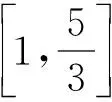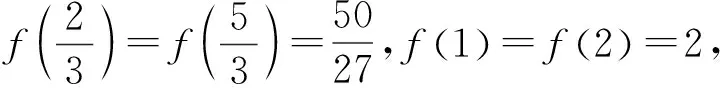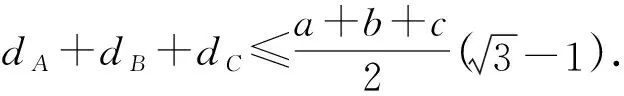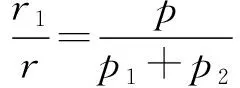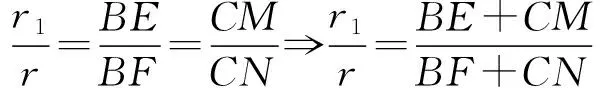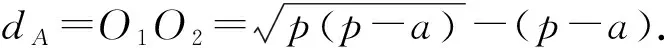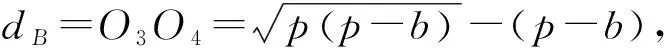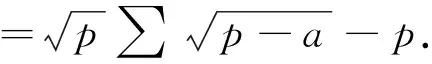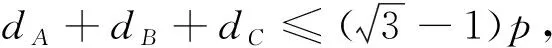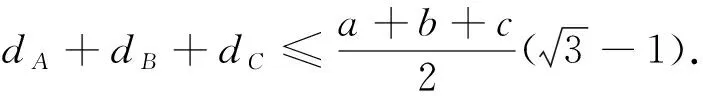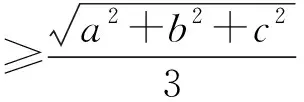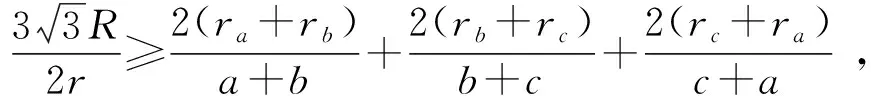数学问题解答
2019年11月号问题解答
(解答由问题提供人给出)
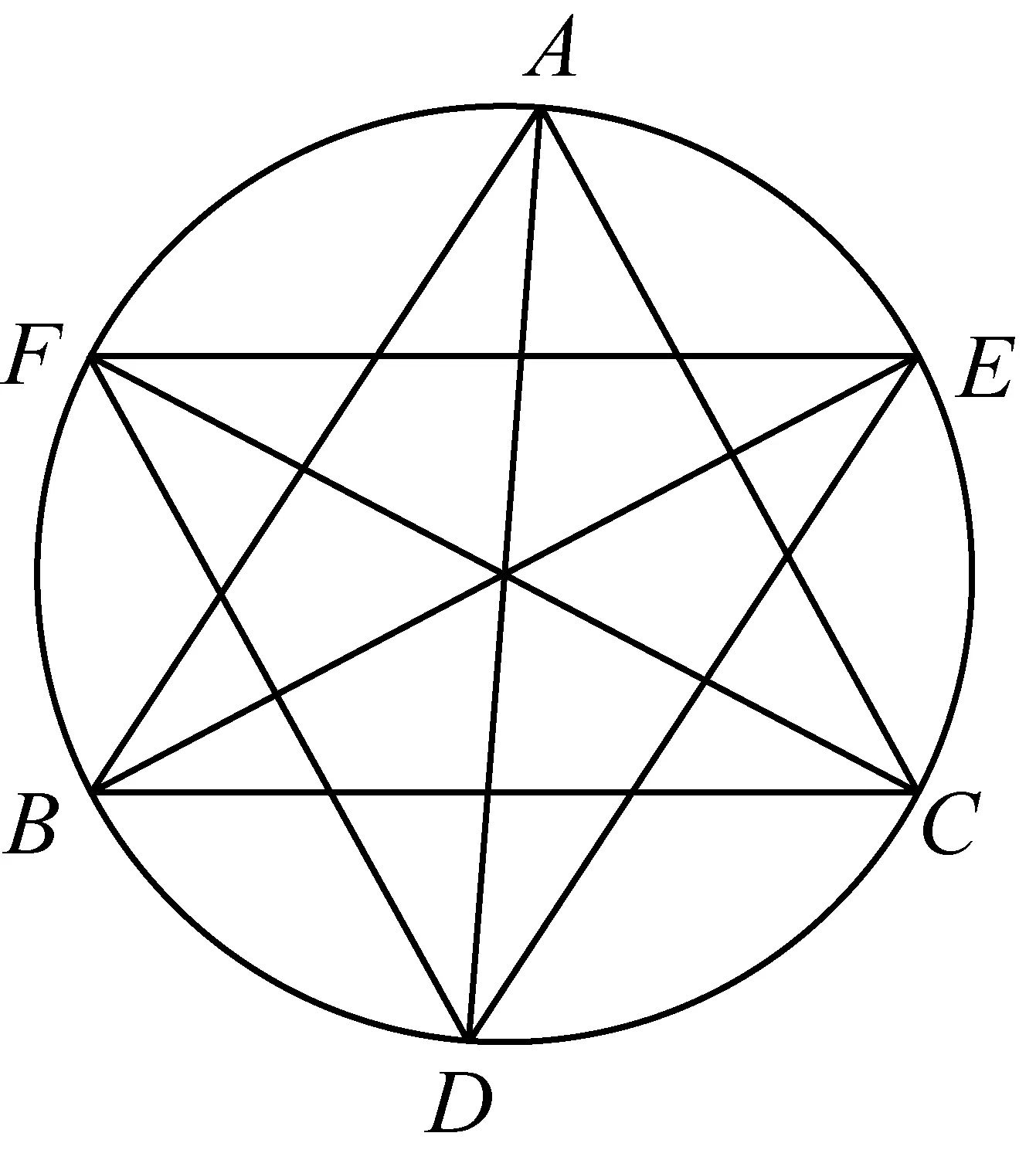
2511已知△ABC的角A,B,C的角平分线分别交边BC、AC、AB的垂直平分线于D、E、F,求证:△ABC的周长≤△DEF的周长.
( 山东省泰安市宁阳第一中学 刘才华 271400)
证明首先证明A,F,B,D,C,E六点共圆.
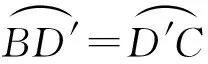
再证明△ABC的周长≤△DEF的周长.
设△ABC的外接圆的半径为R,由正弦定理得△ABC的周长=2R(sinA+sinB+sinC).
在△DEF中,由∠DFE=∠DFC+∠EFC
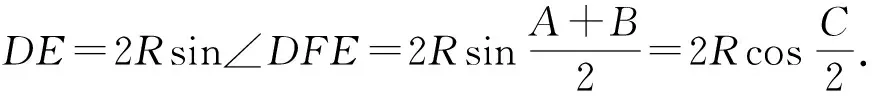
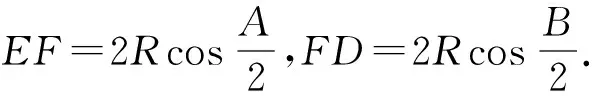

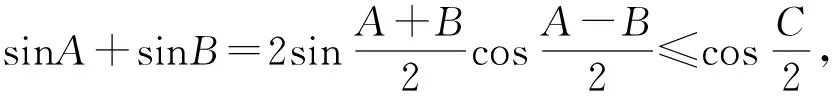
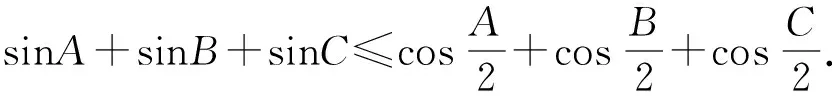
故△ABC的周长≤△DEF的周长.
2512已知正数a,b,c,d满足abcd=1,求证:
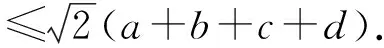
(安徽省岳西县汤池中学 杨续亮 苏岳祥 246620)
证明先构造辅助不等式
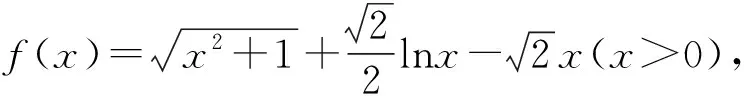
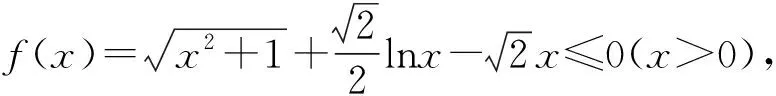
求导
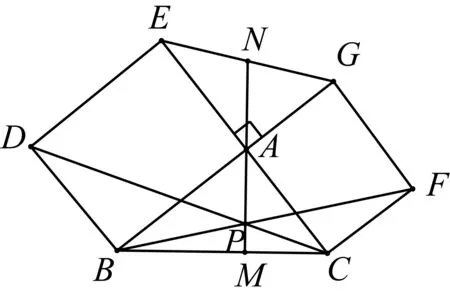
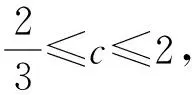
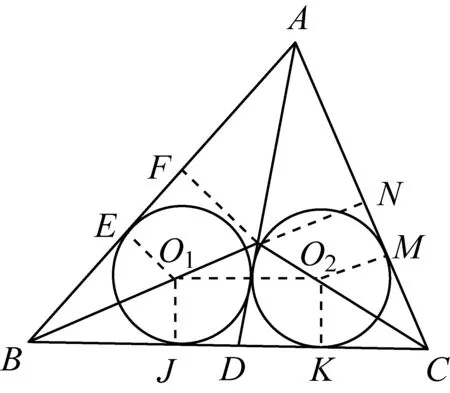
当0 当x>1时, =-(2x4+x2+2x)+1<0, ≤f(x)max=f(1)=0, 以上四式相加可得 因此不等式 得证. 2513如图1,分别以△ABC边AB、AC为一边向△ABC外作矩形ABDE和矩形ACFG,CD交BF于点P.若AB=kAE,AC=kAG,直线AP分别交BC、EG于点M、N.求证:(1)MN⊥BC.(2)点N是EG的中点. (四川省巴中市巴州区大和初中 李发勇 636031) 图1 证明(1)如图2,作AK⊥CD,AS⊥BF. 连结AD、AF、BK、CS、KS. 易证AKBD、ASCF、AKPS四点共圆. 图2 在Rt△ABD和Rt△ACF中, 得tan∠BAD=tan∠CAF, 所以∠BAD=∠CAF, 所以∠BKD=∠BAD=∠CAF=∠CSF, 所以∠BKC=∠BSC,所以BKSC四点共圆, 所以∠BCK=∠BSK=∠PAK. 因为∠APK=∠CPM, 所以∠AMC=∠AKC=90°,所以AM⊥BC. (2)如图2,过点E作EQ∥AG交AN延长线于点Q. 则∠AEQ=180°-∠EAG=∠BAC, ∠EAQ=90°-∠BAM=∠ABC. 所以△EAQ∽△ABC, 所以EQ=AG. 即点N是EG的中点. (四川省成都华西中学 彭艳玲 张云华 610051) 证明因为a,b,c≥0,a+b+c=4,a2+b2+c2=6, 所以6=a2+b2+c2=(a+b)2-2ab+c2 =(4-c)2-2ab+c2, 故ab=c2-4c+5, 由0≤(a-b)2=(a+b)2-4ab =(4-c)2-4(c2-4c+5)=-3c2+8c-4, 有abc=(c2-4c+5)c=c3-4c2+5c. 令f(x)=x3-4x2+5x,x∈R, 则abc=f(c),且f′(x)=3x2-8x+5. (江西省高安市石脑二中 王典辉 330818) 证明设p1、p2、p分别为△ABD、△ADC、△ABC的半周长,r为△ABC的内切圆半径,r1、r2为⊙O1、⊙O2的半径. 因为S△ABC=S△ABD+S△ADC, 有r1p1+r2p2=rp. ① 易知p1+p2=p+AD ② 设I是△ABC的内心,过I作IF⊥AB、IN⊥AC,垂足分别为F、N.过△ABD的内心O1作O1E⊥AB,垂足为E;过△ADC的内心O2作O2M⊥AC,垂足为M.则E、M分别是⊙O1切AB的切点、⊙O2切AC的切点.有 BE=p1-AD,BF=p-b,CM=p2-AD, CN=p-c. 因为O1、I分别为△ABD、△ABC的内心, 所以B、O1、I在一条直线上. 同理C、O2、I也在同一条直线上. 易证△BO1E∽△BIF,△CO2M∽△CIN. ③ 由①、②、③,得AD2=p(p-a) ④ 过O1作O1J⊥BC于J,过O2作O2K⊥BC于K, 有四边形O1JKO2为矩形, 则有O1O2=JK=AD-(p-a), 把上述三式相加得 由柯西不等式有 当且仅当△ABC为等边三角形时,等号成立. 2019年12月号问题 (来稿请注明出处——编者) 2516设x,y,z均为正数,求证: ( 湖北省公安县第一中学 杨先义434300) 2517已知如图1,在⊙O中,弦B1C1∥B2C2,且B1C1=B2C2,O1、O2分别为B1C1、B2C2的中点,点A在C2C1的延长线上,CF1⊥AO1于点F1,与AB1交于点E1,CF2⊥AO2于点F2,与AB2交于点E2.求证: 图1 (北京市朝阳区芳草地国际学校富力分校 郭文征 郭璋 100121) 2518设P是△ABC内的任意点,三条边长、外接圆半径与内切圆半径、点P到三边BC,CA,AB的距离分别为a,b,c,R,r,x,y,z,则有 (天津水运高级技工学校 黄兆麟 300456) 2519在△ABC中,AB>AC>BC,D,E,F,G四点分别在射线AB,CB,AC,BC上,且满足AD=CE=AC及AF=BG=AB,证明:△BDE的外心O1和△CFG的外心O2到点A的距离相等. (河南辉县一中 贺基军 453600) (安徽省太和县第二小学 任迪慧 236630)