立足图像表征 凸显面积计算本质
白丹娜


摘 要:图像表征是学生建立概念、理解概念的有效方式。借助图像表征不仅可以帮助学生推导、理解面积计算公式,更能帮助学生深化面积本质,沟通平面图形面积计算的联系,建立空间观念。笔者以《长方形和正方形面积的计算》为课例,从解构——提取——演变——创建图像表征四个方面来阐述如何让学生完善面积概念、理解公式内涵、内化计算本质、拓展应用途径。
关键词:图像表征;面积计算;小学数学
面积计算是学生进一步理解面积含义,并对面积概念进行应用、提升的过程,更是建立空间观念的学习载体。小学中高段的学生的思维还处在向抽象思维与抽象概括能力发展的过渡期,对面积计算的推导、空间观念的建立还需要具体的图像表征来支撑。立足于图像表征,学生才能有效开展对比、沟通、优化、迁移等活动,理解面积计算的本质。
研究发现,学生在经过一系列的教学活动之后能顺利得出公式并理解公式内涵,而经过一段时间后,大部分学生只记得公式与活动内容,却无法用语言描述公式的本质内涵。那么,如何让学生对面积计算本质的理解不仅停留在课堂中,还能长留于今后的学习中?笔者认为,图像表征弥补了语言描述概括的抽象性的弊端,用更直观的方式体现了面积计算的本质。学生借助图形建构起文字与图形的联系,让学生在今后的面积学习中,用图像代替语言,用图像促进理解,用图像加深记忆。
一、解构重组,完善面积概念
在建立面积概念的教学中,学生对面积的认识建立与具体事物上,而后续的教学重点是对各种平面图形的面积计算。因此,完善平面图形的面积概念显得尤为重要。借助对图形的分割、组合、平移等活动,让学生认识到单位面积与面积之间的关系,凸显面积计算的本质。
师:你是怎么比较的?
生:把多出的格子移到少的那边,这样就变成跟右边一样的图形了。
师:用以多补少的方法,也变成长方形,这个图形面积的大小不变。
师:还有其他方法吗?
生:数里面的格子。
师:小方格的个数相同,表示的面积也相同。
师:如果1个正方形的面积是1平方厘米,这两个图形的面积是几平方厘米?
生:8平方厘米。
师:为什么是8平方厘米?
生:因为里面有8个小正方形,所以是8平方厘米。
师:如果1个正方形的面积是1平方分米呢?(8平方分米)
师:都是这两个图形,怎么一会儿8平方厘米,一会儿8平方分米呢?
师(小结):也就是说,一个图形里面有几个1平方厘米、1平方分米,它的面积就是几平方厘米、几平方分米。单位面积不同,整个图形表示的面积也不同。
上述案例中,借助方格图,学生经历了两个层次的面积概念认知。第一层次:借助方格图对图形中的方格进行平移、拼补、拆分,让学生感受到图形的面积与图形中的小方格的个数有关,与图形的形状无关,渗透了面积的守恒性,初步架构起学生对单位面积与面积之间的联系。第二层次:根据每一个方格表示的单位面积的不同,图形的面积也会发生变化,学生进一步体会到面积的大小与单位面积的大小有关,将两者的关系在方格图中建立起来,加深了学生对面积的认识。
可见,借助熟悉的图像表征,学生能将面积含义、单位面积、面积计算这些零散的知识进行沟通、联系,建构起知识之间的相互联系,完善面积的认知。
二、提取要素,理解公式内涵
完善面积概念是进行系统学习面积知识的起始,是进行面积计算的基础,而了解单位面积与面积之间的关系是探究面积公式本质的关键。面积公式是面积计算方法的优化结果。教师如何在面积公式的推导中,让学生逐步感悟这个优化过程,理解公式的内涵呢?笔者认为,面积公式的推导过程就是一个提取要素的优化过程,而这个优化、提取的过程学生无法用语言进行准确的描述与表达,但在具体的图像中,学生通过观察、比较,能直观看到关键要素,也就更容易提取与理解。
案例二:长方形面积公式推导过程:
1. 小组反馈测量长方形面积(长5厘米,宽3厘米)的方法:
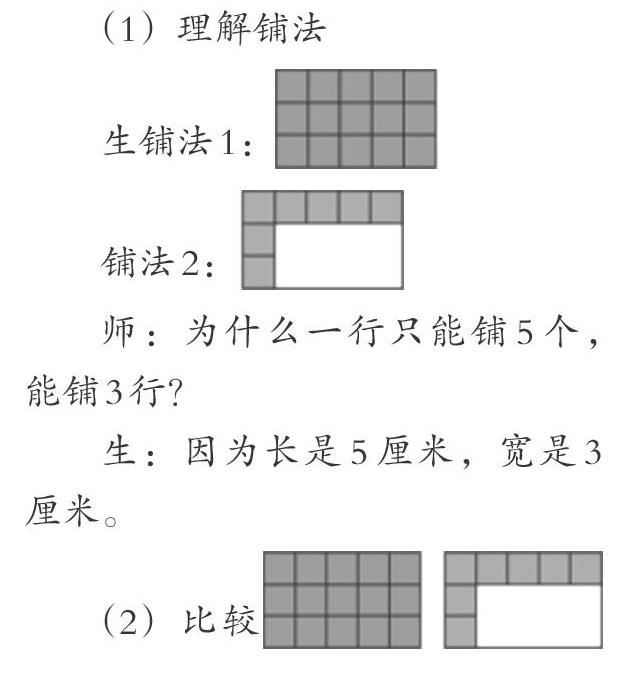
(1)理解铺法
师:为什么一行只能铺5个,能铺3行?
生:因为长是5厘米,宽是3厘米。
2. 摆长方形求面积,找长、宽
师:你摆的长方形的长是几?宽是几?
生:长是5厘米,宽是2厘米。
师:你是怎么知道的?
生:因为一个正方形就是1厘米。一行有5个正方形,就是5厘米,竖的有2个正方形,宽就是2厘米。
生:一行摆了5个,长就是5厘米;一列有4个,宽就是4厘米。
师小结:只要知道一行有几个,有几行,就能知道长和宽。
生:因为长是6厘米,一行能摆6个。宽是4厘米,表示能摆4行。
4. 观察表格,抽象出面积公式。
生:长和宽相乘的得数与面积相同。
生:长乘宽就是长方形面积。
师:长、宽是长度,怎么相乘就变面积了呢?
生:长表示一行有几个,宽表示有几行。
师:也就是说长和宽相乘的得数与小正方形的個数相同。
上述案例中,学生经历了4个活动推导出了长方形面积公式,每一个活动就是一个提取要素的过程。4个过程环环相扣、层层递进,引领学生利用网络图、表格图征抽象出公式,并理解其内涵。
(一)网格图中提取行列要素
学生通过在长方形中铺小正方形的活动,得到了这两种网格图,初步感知到长是几,一行就有几个小正方形,宽是几,一列就有几个小正方形,并通过比较,将方格图优化成行列式的网格图。在优化过程中提取出行列要素,让学生关注一行、一列的小正方形个数,来求小正方形的总数,即长方形的面积,从而初步感悟到长方形面积就是小正方形面积之和。
(二)长方形拼图中提取长宽要素
学生在第2个活动中进行了摆长方形的实践操作活动,并利用2种不同形式的长方形寻找长宽。从寻找长宽,正是长宽要素提取的过程。通过提取长宽,让学生感悟到一行有几个小正方形,长就是几,一列有几个小正方形,宽就是几。与第1个活动的思维相反,帮助学生建立起长宽与行列之间的关系。
紧接着在第3个活动中,让学生经历的想象过程,对图像再次优化,让学生进一步关注长宽与行列之间的关系,理解长宽在面积计算中的含义。
(三)表格图中提取关系要素
学生从理解长宽的含义到理解公式内涵还有一段的距离,教师还需要帮助学生打通两者的关系。借助表格图教师便能将两者之间的关系外显出来,建立起图与文字的关系,将文字表示的关系外化成图像,有助于学生发现和理解公式的内涵。
在第4个活动中学生通过表格中多个长方形面积计算的数据,对比发现长宽与长方形面积的关系,抽象出长方形的面积公式。同时,追问“长和宽表示的是长度,怎么相乘后变成了面积?”进一步让学生思考长宽的含义与面积的关系,并将这种联系以文字和图示的形式表示出来。如下图,借助了图示,学生将公式中长、宽、面积与行、列、总个数之间进行相互沟通与理解,从而理解公式内涵。
学生经历3个要素的提取,从感悟长方形面积与小正方形面积之和的关系,到理解长宽在面积中的含义,最后到打通相互间的关系,理解公式内涵。并且通过图像的形成、优化、理解三个活动,将公式内涵以图像和文字两种形式呈现,帮助学生初步认识面积计算的本质。
三、演变推理,内化计算本质
一种图像表征的建立,通常是在指定的教学活动中或情境中进行,而这种图像表征是具有特定性、唯一性的,甚至会造成思维定势。在面积计算的教学课例中,教师采用的单位面积常常是1平方厘米,形成的图像中的方格也是以1平方厘米的为例,但要让学生真正体会到面积计算的本质是计算单位面积的个数,同时单位面积是多种形式的,就需要我们对建立的图像表征进行变式,丰富学生对图像作用的认识,从而理解面积计算本质。
【变式一】“平移”重组图像
这个长方形的长是( )厘米,宽时( )厘米。面积是( )平方厘米。
【变式二】“扩大或缩小”测量单位
一行能鋪( )个正方形,能铺( )行。长方形面积是( )平方厘米。
上面两种变式中,主要达到两个目的。第一个目的:第一种变式中改变了图像中小方格的位置,让学生更关注长宽与方格边长数之间的关系,从而进行平移重组图像,丰富学生对图像的认知。第二种变式中改变了测量的单位面积,主要目的是打破认为只能用边长是1厘米的正方形才能测量的思维定势。第二个目的:在面积计算时,既可以用面积公式计算长方形面积,也可以用求小正方形面积之和来计算长方形面积,在两种计算方法的对比中让学生进一步体会公式的内涵,理解面积计算的本质。同时感受到面积的守恒性,深化面积概念。
四、多元创建,拓展应用途径
图像表征能帮助学生在解决面积问题时,更易找到解决面积问题的关键与方法,拓展思考途径与方法,也更关注面积计算的本质,全面认识面积度量。
案例四:解决问题(草坪是一块块的草皮拼起来的,每块草皮是边长6分米的正方形。用这样的草拼25块,能铺多大面积?)
从上面学生的作品中我们可以发现:(1)图像相同,面积计算的方法不同。作品1和作品2都创建了长方形图形,但作品1采用了求小正方形面积之和的方法,作品2采用了长方形面积公式的方法。两位学生方法不同,得到的结论却相同。有助于学生丰富面积计算的方法,杜绝方法的单一性,拓展解题途径,也让学生认识到面积的守恒性。(2)图像不同,面积计算的方法相同。作品1和3图像不同,但都采用计算小正方形面积之和的方法,而作品2和4根据图像,得到25块草坪拼成长方形或正方形,都利用面积公式进行计算。通过不同图形之间抽象出相同的计算方法,可以让学生深刻感悟到面积计算的方法的应用范围之广,也对面积计算本质的认识再次深化与理解。
总之,对面积计算本质的理解从以文字描述为主的方式转变为以图像表征为主的方式,更符合学生的认知心理。立足于图像表征,让学生更直观、简易地理解公式内涵,真正做到将本质内涵内化与外化互通,完善概念的理解,提升面积计算本质的理解与运用。
参考文献
[1]葛素儿.通过图像表征促进小学数学理解教学[J].课程教学研究,2012(12).
[2]黄燕舞.在思考与尝试中走进知识本质——长正方形面积公式浅探[J].基础教育参考,2011(20).
[3]叶柱.聚焦数学本质,凸显模型意义——“长方形、正方形面积的计算”课例解读[J].小学教学(数学版),2014(09).

