宏程序在数控车削加工中的应用

李应峰, 宋琳琛

摘 要：宏程序在数控编程中有着广泛的应用。结合两种非圆曲线宏程序编程实例，分析表明：宏程序数控编程具有编程快捷和程序短小精悍的显著特点，尤其适用于一些含非圆曲线的零件的数控编程加工。

关键词：宏程序;数控编程;非圆曲线

DOI：10.16640/j.cnki.37-1222/t.2019.02.009

1 概述

在数控加工中经常要对一些轮廓的表面进行加工，而这些轮廓的表面往往都不是一个平面，可能为：球面结构、凸面结构等。这样我们就要用到一些椭圆、抛物线、渐开线等曲线加工法。这样以来，普通的手工编程方式往往不能满足这些轮廓的加工需求，我们就需要采用宏程序编程，用变量参数代替具体的数值，在加工过程中不断改变变量从而实现普通编程难以实现的功能。而宏程序编程不单可以满足普通编程难以实现的功能，这样编程方式使我们在编程应用起来灵活多变，加工程序也更加简单，是数控加工编程的重要部分。

椭圆是较为典型的非圆曲线，是我们在数控加工经常遇到的曲面之一，也是必须要利用宏程序来才能完成加工的曲面，在数控车和数控铣编程中具有很强的代表性，因此本文将着重分析和说明椭圆曲面中的宏程序编制方法和使用技巧。

2 关于椭圆型曲线的宏程序编辑加工

2.1 椭圆长轴不与工件轴线重合

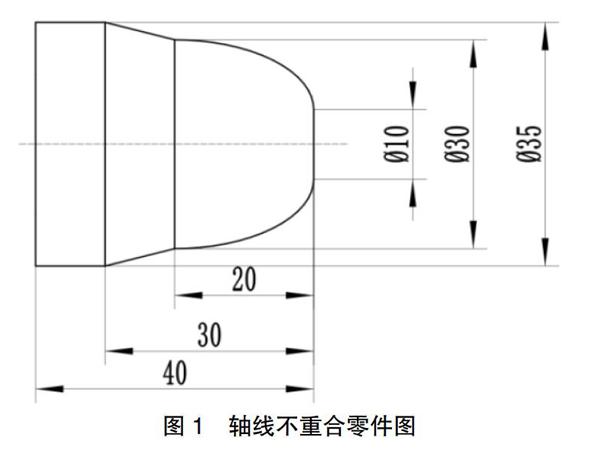
如图1所示零件，材料为硬铝，φ40毛坯锻件棒料。在此仅对椭圆曲线用宏程序进行编程讨论，过程如下：

（1）根据椭圆曲线的函数方程： （X值为半径值）。

则（X值为直径值）。

编程时，必须考虑椭圆中心与编程原点不一致的问题，即所有按上述公式计算出的拟合点坐标都应该加上相应的X和Z偏差值。[1]由图1可知，椭圆中心的坐标值为（X10.0，Z-20.0），从而可得：。

因为是凸圆弧，故取。

（2）定义变量：

#111——椭圆的长轴半径;

#112——椭圆短轴半径;

#113——Z向循环变量;

#115——X坐标变量。

（3）变量运算思路。采用小段直线拟合，以Z向长度0.1mm为一个步距来分段，把Z坐标当为自变量，[2]由上述公式即可计算出所有拟合点的坐标，通过修改步长值的大小可改变曲线加工精度与表面粗糙度。

（4）参考程序：

图1零件椭圆曲线部分的参考宏程序如下：

%

O0001

N10 #111=20

N20 #112=10

N30#113=20

N40 IF[#113LT0]GOTO100

N50#114=SQRT[#111*#111-#113*#113]

N60 #115=#112*#114/#111

N70 G01X[10+2*#115+#150]Z[#113]

N80 #113=#113-0.1

N90 GOTO40

N100 G00U20.0Z5.0

N110 M99

%

2.2 椭圆的长半轴与工件轴线重合

参考程序：

%

O0002

N10 G98M03S1000T0404F200.0

N20G00X45.0Z2.0

N30 #150=4.0

N40 IF[#150LT1]GOTO80

N50 M98 P0002

N60 #150=#150-3.0

N70 GOTO40

N80G00X45.0Z2.0

N90S1450F100.0

N100 #150=0.0

N110 M98P0002

N120 G00X150.0Z55.0

N130 M05

N140 M30

%

%

O0003

N10 #111=20.0

N20#112=10.0

N30#113=20.0

N40 IF[#113LT0]GOTO100

N50#114=SQRT[#111*#111-#113*#113]

N60 #115=#112*#114/#111

N70 G01X[2*#115+#150]Z[#113]

N80 #113=#113-0.1

N90 GOTO40

N100 G00U20.0Z20.0

N110 M99

%

3 主要結论

通过以上讨论分析可知，宏程序能用变量编程，程序精炼，通用性强等特点，在解决非圆曲线编程问题上优势突出，可以用于解决实际生产中特殊曲面编程问题，对提高生产效率有重大意义。

参考文献：

[1]韩加好.数控编程与操作技术[M].北京：冶金工业出版社，2008.

[2]王洪亮.数控车床宏程序编程应用实例[J].科技资讯，2007（04）.