幼儿前滑步动作发展特征的函数型数据分析

张百发，周兴龙，席健夫，罗冬梅

（北京体育大学 运动人体科学学院，北京 100084）

幼儿时期是基本动作技能发展、成熟关键期，探索该阶段基本动作技能发展特征对幼儿提高基本动作技能、掌握各类运动、增强体力活动及养成终身运动习惯至关重 要（Hands，2008；Holfelder et al.，2014；Payne et al.，2008；Reinert，2013）。前滑步作为幼儿接触的首个不对称位移技能，通常在两岁左右开始发展，广泛出现于游戏、下楼梯/斜坡等情景中（Fiers et al.，2013），若前滑步动作发展滞后，会导致幼儿体力活动不足，进而造成体质健康方面问题（Foulkes et al.，2015）。

幼儿动作发展领域中，学者们通常以观察、归纳前滑步动作发展序列的方法，定性描述前滑步发展特征。动作发展序列是指特定生理年龄阶段儿童完成基本动作技能时所表现出的共同特征，将这些特征按照先后顺序排列即为该动作技能发展序列（王兴泽等，2014），分为反映儿童整体动作特征的整体序列，以及体现上肢、躯干或下肢特定部位动作特征的部分序列。Snapp（1980）率先采用整体序列法定性描述儿童前滑步整体动作特征，并划分出3个发展阶段（表1），该发展序列受到学者们广泛认同（Getchell et al.，2004；Peck et al.，1997）。定性研究可以提供前滑步不同发展阶段的动作模式信息，但容易受观察者的主观性影响，需要结合客观定量分析方法。幼儿前滑步运动学数据背后是完整连续过程，采用传统截面统计会忽略样本间有序性，故需要更契合的统计工具——函数型数据分析。

函数型数据分析是加拿大统计学会主席Ramsay（2005）开创的新型统计方法，广泛应用于动作发展、动作技术分析（林辉杰等，2012）、运动损伤诊断（Donoghue et al.，2008；Epifanio et al.，2008）以 及 康 复 效 果 评 价（Sánchez-Sánchez et al.，2018）等研究。函数型数据分析核心思想是把观测数据函数看作整体，而不仅是个体观测值顺序排列。相较于传统截面统计，函数型数据分析既体现系统本身连续性又满足能量有限原理。同时作为衔接连续动态分析与数字信号处理的重要工具，容易与回归分析、模式识别技术相结合（向馗等，2014）。

因此，本文通过2年纵向跟踪测试，基于动作发展序列理论定性归纳3.5～5.5岁幼儿下肢动作发展序列；同时采用函数型数据分析方法提取不同发展阶段幼儿下肢运动学特征，探讨函数型数据分析技术在幼儿前滑步研究中的应用效果，以期未来结合机器学习技术研发幼儿动作发展自动评价工具。

1 研究对象与方法

1.1 受试者

本研究选取北京市城区2所幼儿园53名3.5岁幼儿（男孩27人，女孩26人），年龄纳入标准为测试日期减去出生日期所得天数在3岁6个月前后15天内。于2015年10月—2017年10月跟踪测试2年，测试间隔时间为1年，共进行3次测试。受试者均为健康幼儿，无认知、动作发展迟缓以及身体发育障碍等问题。追踪2年期间由于转学、生病等客观因素，最终完整参与3次测试的受试者共计16名（男孩10人，女孩6人）。采用卡方检验比较最终样本与原来样本性别情况，二者差异不具有统计学意义（P=0.417），故最终样本为原样本的无偏代表。

1.2 测试仪器

应用6镜头红外高速运动捕捉系统（100 Hz，Qualisys，瑞典）采集幼儿前滑步时人体运动学数据。采用HDR-PJ600摄像机（50 Hz，Sony，日本）从侧面记录幼儿前滑步动作视频。

1.3 测试过程

测试前记录受试者基本信息（姓名、性别），测试人员为幼儿穿上同款紧身裤及统一测试鞋后，告知幼儿测试流程，并口头引导幼儿热身熟悉动作。热身结束，由同一名专业实验人员按照Helen Hayes方案粘贴27个反光标志点（颅顶点，第七颈椎，第五腰椎，两侧肩峰点，两侧肱骨外上髁，两侧桡骨茎突，两侧髂前上嵴，两侧大腿前侧，两侧股骨外上髁，两侧股骨内上髁，两侧胫骨前缘中点，两侧外踝，两侧内踝，两侧足跟和足尖）。开始测试时，专业测试人员示范引导受试者在自然速度下前滑步往返通过测试区域（图1）；受试者自然、无停顿前滑步通过测试区域视为1次有效数据，共采集4次有效数据。

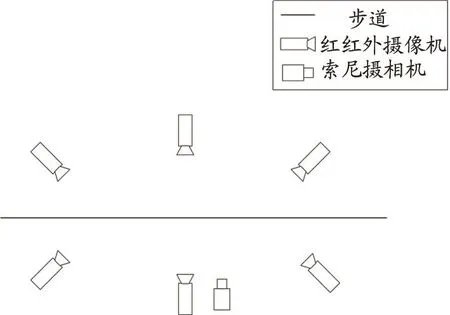
图1 测试现场示意图Figure 1.The Schematic Diagram of Test Field

1.4 数据处理

1.4.1 动作部分发展序列定性分析

根据前滑步4个特征时刻（跟随腿着地、引导腿着地、跟随腿离地、引导腿离地）将前滑步分为跟随腿支撑期、双支撑期、引导腿支撑期、腾空期4个动作技术阶段（图2）。

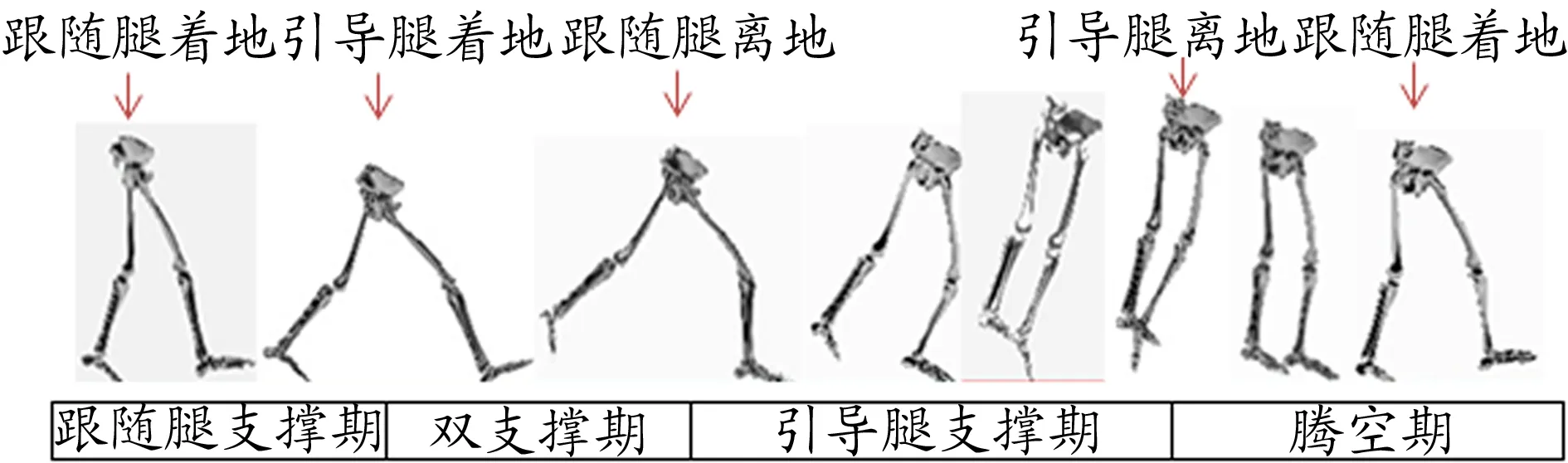
图2 前滑步动作技术分析示意图Figure 2.Technique Analysis on Galloping

选取幼儿在前滑步途中一个完整动作周期测试视频反复仔细观察。参照前人研究（Payne et al.，2012），依据部分序列发展理论，从以下3个方面：特征时刻下肢状态、腾空阶段下肢状态、跟随腿与引导腿位置关系观察分析幼儿前滑步动作，总结幼儿前滑步下肢动作特征。

1.4.2 运动学数据获取

运动学参数采用Visual 3D软件计算处理。根据标志点坐标建立下肢多刚体模型，采用欧拉角计算方法获得下肢关节三维角度。将下肢关节矢状面角度按一个动作周期时长（跟随腿着地至跟随腿再次着地）进行标准化处理。

1.4.3 函数型数据分析

函数型数据分析在matlab R2015b平台下，采用FDA的FPCA工具包编程实现（Ramsay，2018）。前滑步属于周期性动作，故采用151个3阶傅里叶基将下肢关节角度时间序列曲线拟合为函数（Donoghue et al.，2008），平滑参数设为e-7。随后将函数降维分解成若干主元，具体公式如下：

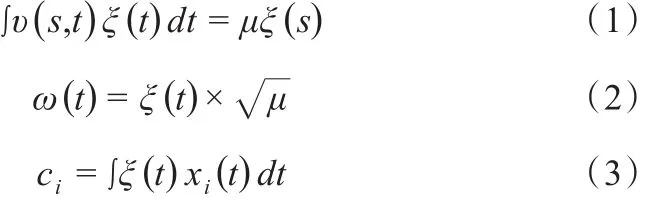
式（1）中：υ(s，t)为函数变量的协方差函数，ξ(t)为特征函数，μ为主元协方差矩阵；式（2）中：ω(t)为主元加权权重系数函数，即以主成分特征值为权重的特征函数；式（3）中：ci为原始函数变量xi(t)在各主元上的得分。通过对上述矩阵的特征方程进行求解，计算出各主元对应的特征值及其特征函数。主元数量确定标准为累积贡献率达到95%且各主元特征值大于1（Ryan et al.，2006）。为了便于对主元解释，采用varimax旋转方法（Jolliffe，2002）及连续配准（Ramsay et al.，1998）消除相位变异性。

1.4.4 数理统计

采用单因素方差分析，分别比较不同前滑步发展阶段幼儿下肢关节角度时间序列曲线主元得分，后续检验采用LSD法，显著性水平设为0.05；采用逐步判别分析，将方差分析中不同前滑步发展阶段幼儿具有显著性差异的下肢关节角度曲线主元得分作为自变量，前滑步发展阶段作为分组因变量，筛选出反映前滑步发展特征的敏感指标，数据分析采用SPSS 20.0软件。

2 结果

2.1 幼儿前滑步动作部分发展序列定性分析

通过对所有幼儿前滑步动作视频观察分析、比较以及归纳总结，参照Sapp研究中归纳的前滑步整体发展序列（表1），将3～6岁幼儿前滑步下肢动作划分为3个发展阶段，各阶段特征见表2。图3为幼儿前滑步动作发展阶段的年龄分布比例图，该图显示各年龄组岁组幼儿在3个阶段均有分布。

表1 前滑步动作整体发展序列（Sapp,1980）Table 1 Developmental Sequences for Galloping：Total Body Approach

表2 幼儿前滑步动作部分发展序列Table 2 Developmental Sequences for the Galloping of Preschoolers：Component Approach

2.2 不同发展阶段下肢各关节角度时间序列曲线函数型数据分析

2.2.1 引导腿髋关节角度时间序列曲线函数型数据分析

图4为幼儿前滑步引导腿髋关节角度时间序列曲线主元分析结果，经过连续配准剔除相位变异串扰，反映各主元幅度变异特性。图中实线为关节角度变化均值曲线，“+”曲线是在均值基础上加上主元适当倍数，“-”曲线是在均值基础上减去主元适当倍数（梁银双等，2017）。从“+”曲线和“-”曲线包围区域可以看出变异发生位置及大小。当个体主元得分为正值时，其关节角度变化曲线接近“+”曲线，反之接近“-”曲线。

幼儿前滑步引导腿髋关节角度时间序列曲线降维成两个主元，特征值为61.7、11.4，分别表达82.2%、15.1%的变异性，累积贡献率97.4%。引导腿髋关节角度主元一幅度变异集中在波谷位置，结果显示，不同动作发展阶段幼儿该主元得分差异不具有统计学意义（图4 i）。引导腿髋关节角度主元二幅度变异集中在波峰位置，结果显示，第3阶段幼儿该主元得分低于第1阶段幼儿，二者差异具有统计学意义（P=0.02，图4 ii）。

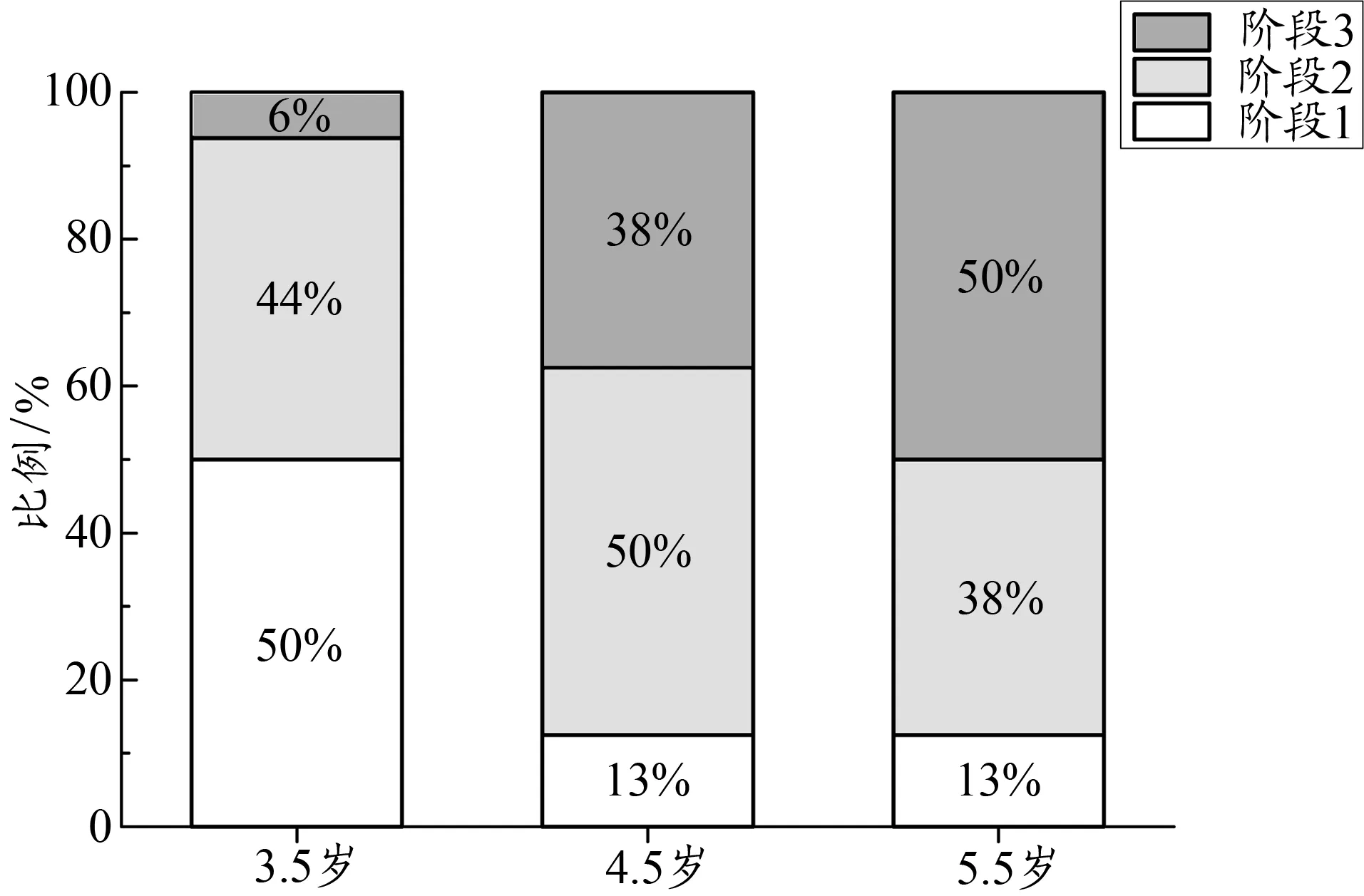
图3 幼儿前滑步动作发展阶段年龄分布比例Figure 3.Age Distribution of the Development Stage of Preschool Children's Galloping Action

2.2.2 引导腿膝关节角度时间序列曲线函数型数据分析

图5为幼儿前滑步引导腿膝关节角度时间序列曲线主元分析结果，该关节角度时间序列曲线降维成两个主元，特征值为105.6、11.6，分别表达86.3%、9.5%的变异性，累积贡献率95.8%。引导腿膝关节角度主元一幅度变异集中在第1个波峰上升、第2个波峰下降两时段，结果显示，第1阶段幼儿该主元得分低于第2阶段、第3阶段幼儿，差异具有统计学意义（P＜0.01，P＜0.01，图5 i）。引导腿膝关节角度主元二幅度变异集中在波谷位置，结果显示，第1阶段幼儿该主元得分高于第2阶段、第3阶段，差异具有统计学意义（P＜0.01，P=0.02，图5 ii）。

2.2.3 引导腿踝关节角度时间序列曲线函数型数据分析

图6为幼儿前滑步引导腿踝关节角度时间序列曲线主元分析结果，该关节角度时间序列曲线降维成3个主元，特征值为40.3、9.2、4.3，分别表达72.7%、16.6%、7.8%的变异性，累积贡献率97.1%。引导腿踝关节主元一幅度变异集中在第2个波谷谷值位置、第1个波峰上升位置两个时段，结果显示，第1阶段幼儿该主元得分低于第3阶段幼儿，二者差异具有统计学意义（P=0.05，图6 i）。引导腿踝关节主元二幅度变异集中在第2个波峰峰值位置，结果显示，第1阶段幼儿该主元得分高于第3阶段幼儿，二者差异具有统计学意义（P=0.01，图6 ii）。引导腿踝关节主元三幅度变异集中在第1个波峰时段，结果显示，不同动作发展阶段幼儿该主元得分差异不具有统计学意义（图 6 iii）。

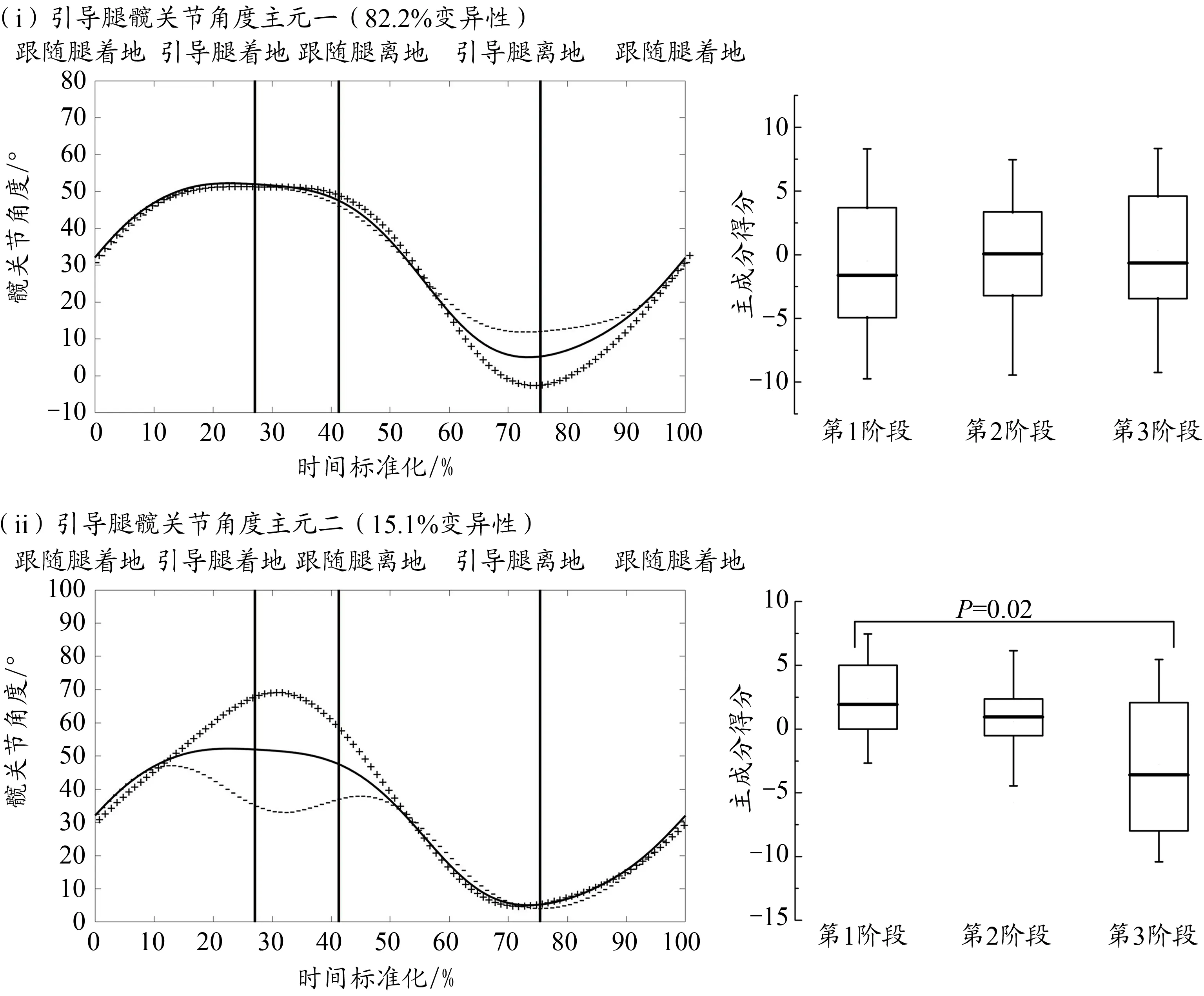
图4 前滑步引导腿髋关节角度均值±权重系数及不同动作发展阶段主元得分Figure 4.Adding and Subtracting a Multiple of the FPC to the Mean Lead Hip Joint Angle Curve and the Distribution of FPC Scores with Respect to Developmental Stage

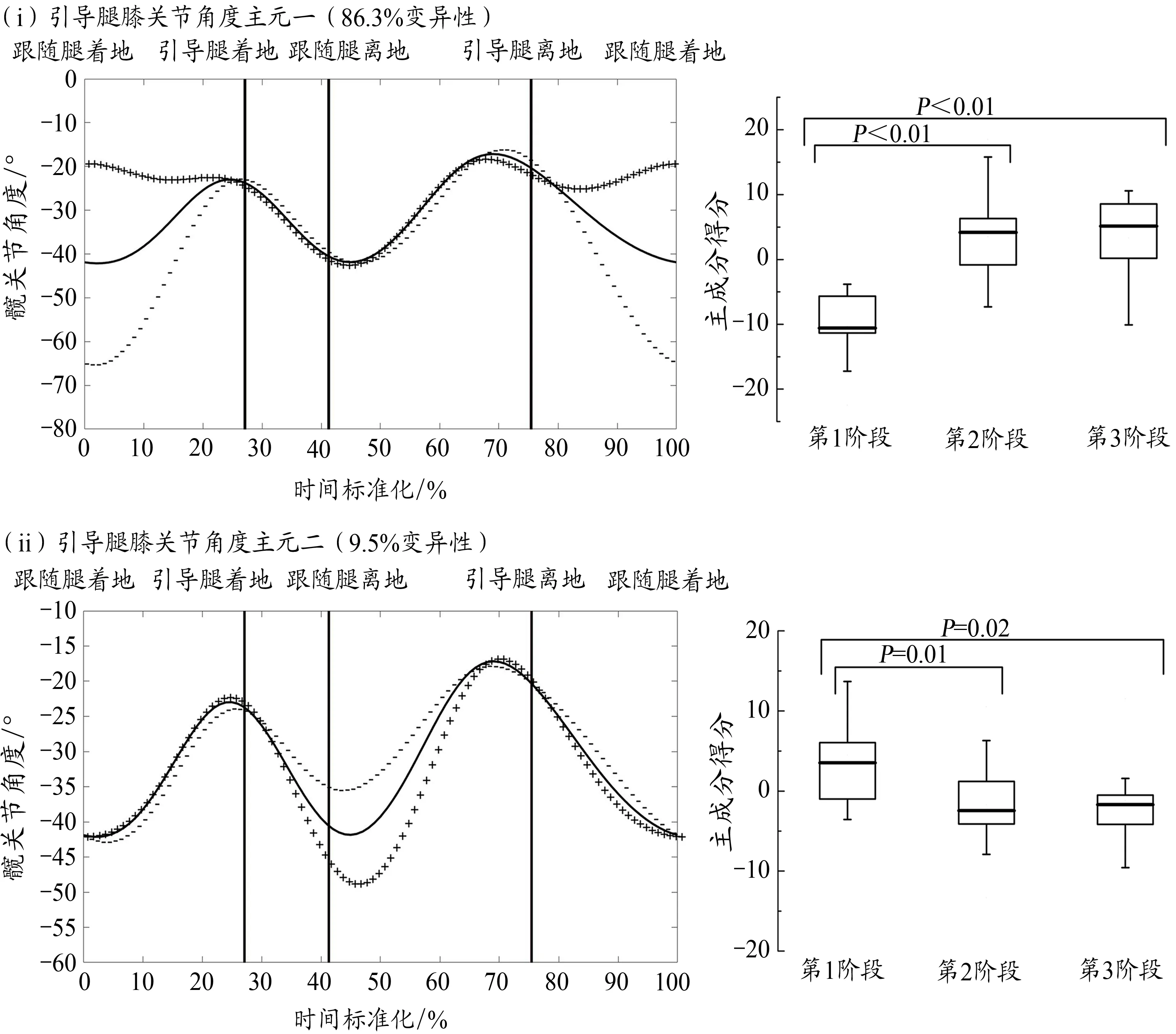
图5 前滑步引导腿膝关节角度均值±权重系数及不同动作发展阶段主元得分Figure 5.Adding and Subtracting a Multiple of the FPC to the Mean Lead Knee Joint Angle Curve and the Distribution of FPC Scores with Respect to Developmental Stage

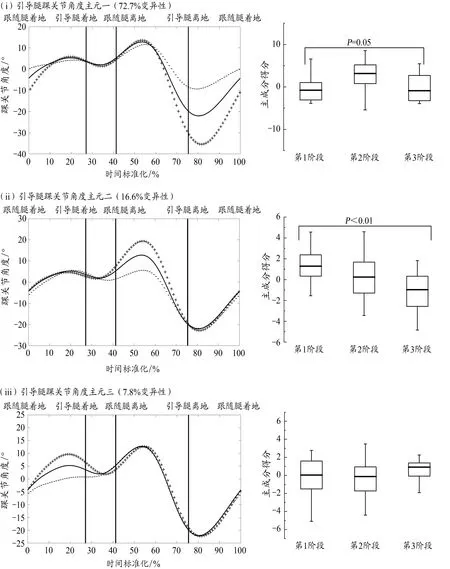
图6 前滑步引导腿踝关节角度均值±权重系数及不同动作发展阶段主元得分Figure 6. Adding and Subtracting a Multiple of the FPC to the Mean Lead Ankle Joint Angle Curve and the Distribution of FPC Scores with Respect to Developmental Stage

2.2.4 跟随腿髋关节角度时间序列曲线函数型数据分析

图7为幼儿前滑步跟随腿髋关节角度时间序列曲线主元分析结果，该关节角度时间序列曲线降维成两个主元，特征值为96.8、6.4，分别表达91.5%、6.0%的变异性，累积贡献率97.5%。跟随腿髋关节角度主元一幅度变异集中在波峰峰值位置，结果显示，第1阶段幼儿该主元得分高于第3阶段幼儿，二者差异具有统计学意义（P＜0.01，图7 i）。跟随腿髋关节角度主元二幅度变异集中在波谷谷值位置，结果显示，不同动作发展阶段幼儿该主元得分差异不具有统计学意义（图7 ii）。

2.2.5 跟随腿膝关节角度时间序列曲线函数型数据分析

图8为幼儿前滑步跟随腿膝关节角度时间序列曲线主元分析结果，该关节角度时间序列曲线降维成两个主元，特征值为199.1、16.7，分别表达87.9%、7.4%的变异性，累积贡献率95.3%。跟随腿膝关节角度主元一幅度变异集中在第1个波峰、第2个波谷两个时段，结果显示，第1阶段幼儿该主元得分低于第2阶段、第3阶段幼儿，差异具有统计学意义（P＜0.01，图8 i）。跟随腿膝关节角度主元二幅度变异集中在第一个波谷时段，结果显示，不同动作发展阶段幼儿该主元得分差异不具有统计学意义（图8 ii）。

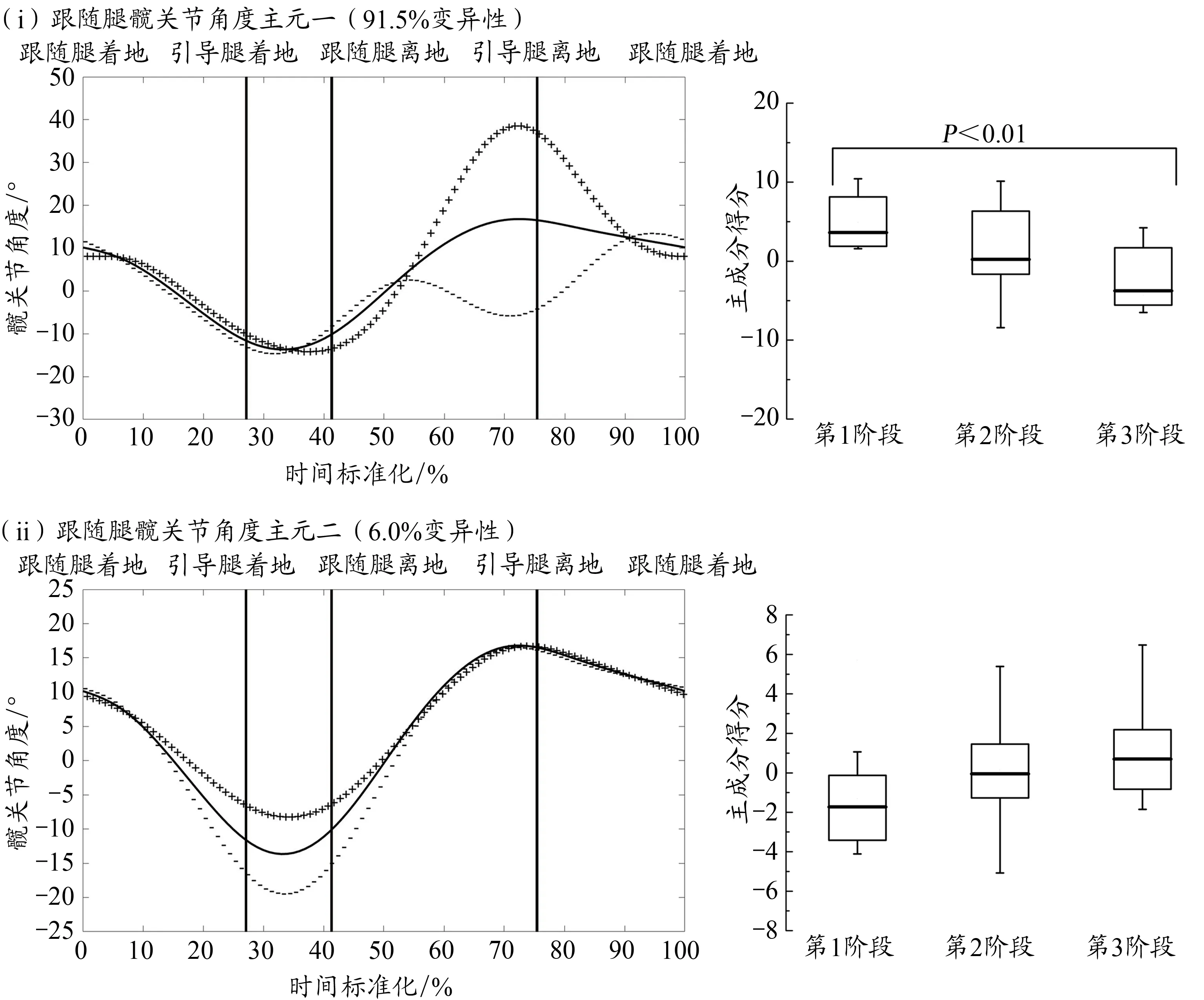
图7 前滑步跟随腿髋关节角度均值±权重系数及不同动作发展阶段主元得分Figure 7.Adding and Subtracting a Multiple of the FPC to the Mean Trail Hip Joint Angle Curve and the Distribution of FPC Scores with Respect to Developmental Stage

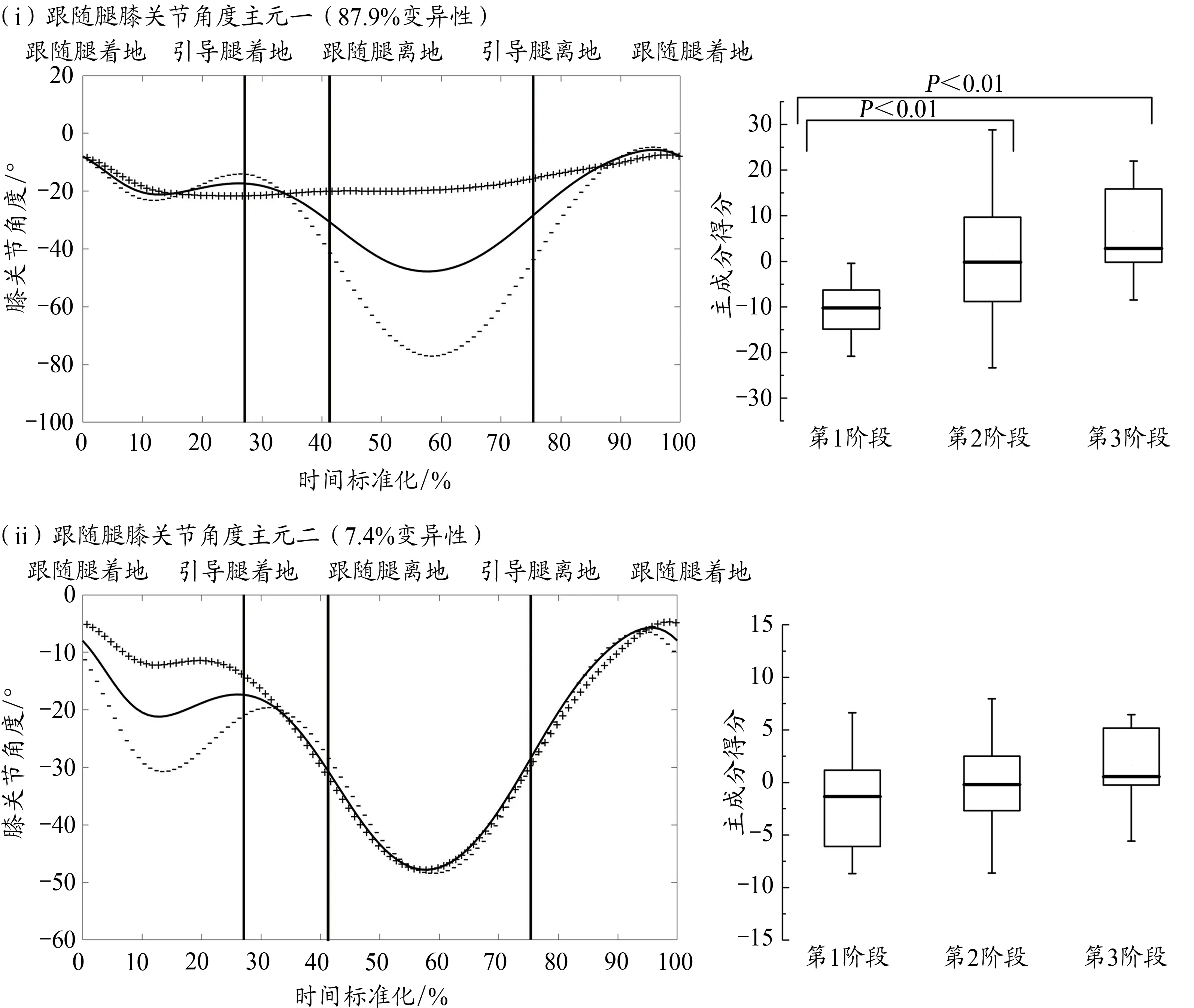
图8 前滑步跟随腿膝关节角度均值±权重系数及不同动作发展阶段主元得分Figure 8.Adding and Subtracting a Multiple of the FPC to the Mean Trail Knee Joint Angle Curve and the Distribution of FPC Scores with Respect to Developmental Stage

2.2.6 跟随腿踝关节角度时间序列曲线函数型数据分析

图9为幼儿前滑步跟随腿踝关节角度时间序列曲线主元分析结果，该关节角度时间序列曲线降维成4个主元，特征值为43.6、11.3、9.9、3.8，分别表达62.8%、16.2%、14.3%、5.5%的变异性，累积贡献率98.8%。跟随腿踝关节角度主元一幅度变异集中在第1个波谷时段，结果显示，第1阶段幼儿该主元得分高于第2阶段幼儿，二者差异具有统计学意义（P=0.01，图9 i）。跟随腿踝关节角度主元二幅度变异集中在第1个波峰峰值位置，结果显示，不同动作发展阶段幼儿该主元得分差异不具有统计学意义（图9 ii）。跟随腿踝关节角度主元三幅度变异集中在第2个波谷时段，结果显示，不同动作发展阶段幼儿该主元得分差异不具有统计学意义（图9 iii）。跟随腿踝关节角度主元四幅度变异集中在第2个波峰时段，结果显示，第1阶段幼儿该主元得分低于第2阶段幼儿，即第1阶段幼儿引导腿支撑期、腾空期跟随腿踝关节背屈角度最大值及跟随腿踝关节运动幅度大于第2阶段幼儿，二者差异具有统计学意义（P＜0.01，图9 iv）。?

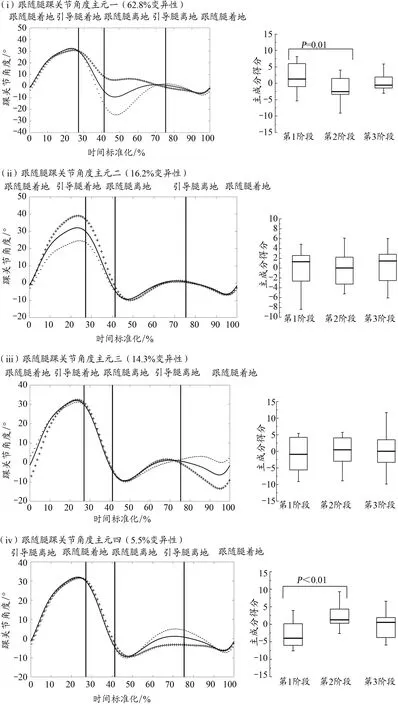
图9 前滑步跟随腿踝关节角度均值±权重系数及不同动作发展阶段主元得分Figure 9.Adding and Subtracting a Multiple of the FPC to the Mean Trail Ankle Joint Angle Curve and the Distribution of FPC Scores with Respect to Developmental Stage

表3显示，经过对幼儿下肢关节角度主元得分逐步判别分析，最终筛选出3个主元作为幼儿前滑步动作发展特征敏感指标，分别为引导腿髋关节主元二、膝关节主元一及跟随腿髋关节主元一。表4为检验判别效果的判别分类结果矩阵，结果显示，判断幼儿前滑步动作发展阶段整体正确率为79.2%，第1阶段幼儿全部被正确判别。

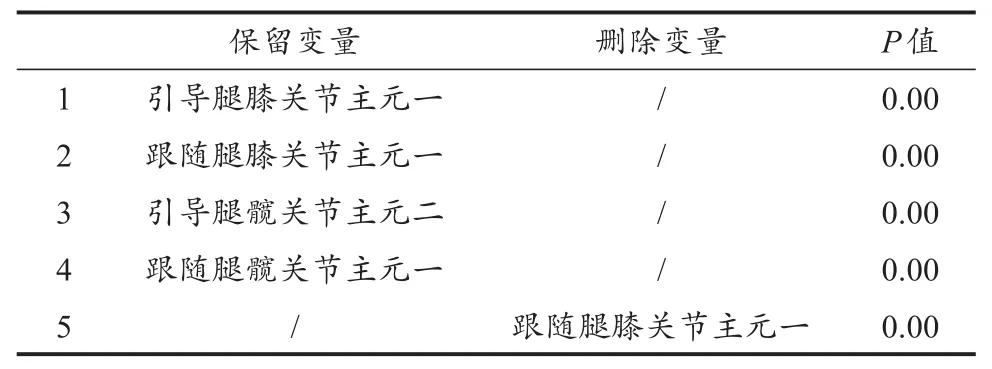
表3 逐步判别分析步骤及结果Table 3 The Results for Each Step of The Stepwise Discriminant Analysis

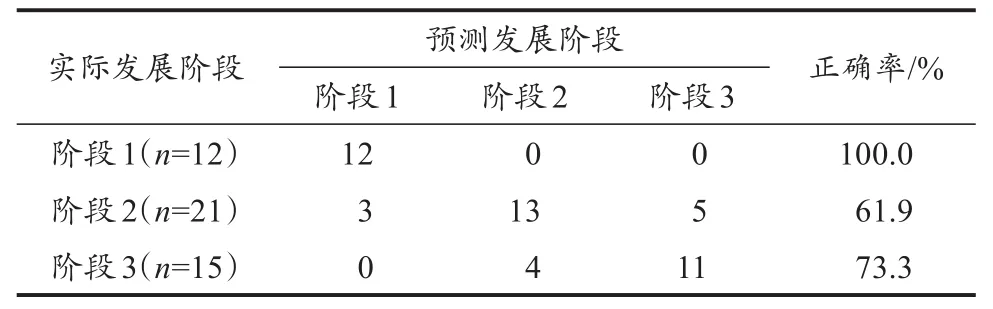
表4 判别分析验证结果Table 4 Classification Results from Discriminant Analysis

3 讨论

动作发展序列理论由涵盖“阶段”等概念的机体发展理论演变发展而来，通过识别个体生命过程中重复某项动作任务表现的动作特征，从而探索动作技能形成过程中动作模式发生的本质变化（Roberton，1977）。动作发展学者普遍认为，年龄不是幼儿动作发展的唯一基准，相同生理年龄幼儿动作特征不尽相同。张莹（2013）通过横向观察归纳3～6岁幼儿投掷动作特征及发展趋势发现，幼儿投掷动作可归纳为10种类型，并分布在各生理年龄段。范雪（2017）通过横向观察总结3～6岁幼儿跑步动作发展特征发现，幼儿跑步的发展水平存在3个阶段，且分布在各生理年龄段。本研究结果显示，3.5～5.5岁幼儿前滑步下肢动作发展序列可分为3个阶段，且不同年龄段幼儿前滑步下肢发展水平在3个阶段均有分布。由此可见，幼儿虽然经历相似动作发展序列，但个体动作发展水平在不断提高过程中所达到的水平仍取决于个体遗传、环境、所受到约束的影响（王兴泽等，2014）。本研究结果显示，5.5岁组幼儿前滑步处于第3阶段比例最高，处于第1阶段比例较4.5岁组未减少，说明部分幼儿前滑步动作发展产生瓶颈，如果没有正确引导可能会导致幼儿前滑步动作滞留在该阶段，提示在幼儿群体中开展体育教学活动需要识别每个孩子动作技能成熟度，以便更好地促进幼儿发展。

函数型数据分析通过将离散运动数据序列转化为连续函数，找出运动的连续特征信息（苏本跃等，2017）。Ryan等（2006）将幼儿纵跳时膝关节角度时间序列通过函数型数据分析转化为连续函数并降维成三阶主元，发现膝关节主元三可作为区分幼儿纵跳发展阶段的敏感指标，该指标对应人的牵张收缩循环能力。本研究筛选出幼儿前滑步动作下肢关节角度敏感指标为引导腿髋关节主元二、引导腿膝关节主元一和跟随腿髋关节主元一。引导腿髋关节主元二变异时段对应跟随腿着地时刻，人体重心前移，引导腿向前方摆动过程，该主元得分反映摆动过程中髋关节运动幅度、屈曲角度最大值。本研究结果显示，第1阶段幼儿该主元得分高于第3阶段，即第1阶段幼儿引导腿向前摆动过程中髋关节运动幅度、屈曲最大值较第3阶段大，提示第1阶段幼儿支撑阶段重心起伏过大。引导腿膝关节主元一变异时段对应引导腿离地时刻，引导腿自由摆动过程，该主元得分反映摆动过程中膝关节运动幅度、屈曲角度最大值。本研究结果显示，第1阶段幼儿该主元得分低于第2阶段、第3阶段，即第1阶段幼儿引导腿自由摆动过程中膝关节运动幅度、屈曲角度最大值较第2阶段、第3阶段大，提示第1阶段幼儿引导腿在摆动过程中小腿发生折叠。该指标与定性描述呼应，位于发展起始阶段的幼儿前滑步通常表现类似缺省的跑步模式，腾空阶段两侧小腿会发生向后折叠，因此跟随腿着地时刻，引导腿仍保持折叠状态。跟随腿髋关节主元一变异时段对应跟随腿蹬离地面后向前自由摆动过程，该主元得分反映跟随腿摆动过程中髋关节运动幅度、屈曲角度最大值。本研究结果显示，第1阶段幼儿该主元得分高于第3阶段，即第1阶段幼儿引导腿向前摆动过程中髋关节运动幅度、屈曲最大值较第3阶段大，提示第1阶段幼儿跟随腿摆动幅度过大。该指标与第1阶段幼儿腾空阶段跟随腿会超越引导腿定性描述呼应。

本研究详细探讨函数性主元分析在提取幼儿动作发展动作特征的应用条件、参数设置、统计量诠释等，并取得较好效果，认为其是一种能应用于量化识别幼儿动作发展阶段的工具手段。后期可考虑结合机器学习中支持向量机、决策束、人工网络等分类器算法对人体动作行为进行识别（苏本跃等，2017），从而为幼儿动作发展自动评价工具建立提供算法帮助。性别、年龄是幼儿动作技能发展重要变量，后续研究可考虑扩大样本量来探讨不同年龄、性别幼儿前滑步动作发展特征差异。

4 结论

1）3.5 ～5.5岁幼儿前滑步下肢动作发展序列可以分为3个阶段，相同年龄段幼儿前滑步动作发展水平不同。

2）对函数型数据分析方法在提取幼儿前滑步动作发展特征中的应用进行初步探索，筛选出引导腿髋关节角度主元二、引导腿膝关节角度主元一及跟随腿髋关节角度主元一可以作为前滑步动作阶段划分的敏感指标，为定量评价幼儿动作发展水平提供新型技术手段。