热效应下形状记忆合金驱动的磁流变液与滑块摩擦复合传动研究

黄 金，谢 勇，王 西，姚 华

（重庆理工大学 机械工程学院，重庆 400054）

磁流变液（简称MRF）作为一种新型智能材料，在磁场作用下，其力学特性可以迅速变化。从微观角度来说，就是悬浮磁颗粒在磁场的作用下相互作用，形成一种抵抗剪切变形或流动的结构。这种材料的变化表现为表观黏度随磁场作用而迅速增加，当磁场撤去，MRF又迅速恢复为牛顿流体，这就是MRF的流变特性。MRF的整个变化过程具有可逆、可控、迅速等多个特点，基于该特性，其被广泛应用于各种传动和制动器中［1］。

针对基于MRF的剪切屈服应力传递转矩，目前国内外学者进行了大量研究。Huang等［2］分析了MRF制动器和离合器的工作原理，建立了力学模型，分析了MRF传递转矩能力，提出了MRF器件关键几何尺寸的设计方法。Farjoud等［3］分析了MRF在制动器中的流动及MRF屈服面的变化，揭示了MRF在圆盘间流动的本质。Doruk等［4］将制动器的磁路设计成蛇形，使得同等尺寸的制动器制动转矩大大增加。Tran等［5］介绍了一种MR制动器的设计新方法，使得设计出的制动转矩比常规制动器高1倍。黄金等［6］基于MRF的Bingham模型分析了MRF在偏心圆筒中的流动，根据一维雷诺方程，建立了MRF在偏心圆筒中的剪切应力方程，并对剪切应力在偏心圆筒中产生的制动转矩方程进行了推导。郑军［7］根据Bingham粘塑体模型和Navier-Stokes方程，对两圆筒间MRF的瞬态流场进行数值计算，分析了流变响应时间的影响因素，并测试了传动装置的动态响应性能。乔臻等［8］提出了一种SMA驱动的MRF自发电传动方法，可自行对MRF施加磁场，并建立了输入转速与发电电流的关系以及输出转矩与输入、输出转速的关系。杨岩等［9］给出了盘式MRF制动器的设计方法，推导了MRF产生制动力矩的方程，得出了盘式MRF制动器中MRF体积、厚度等的计算公式。

智能材料SMA发展至今，众多学者从不同角度，采用不同方法结合实验建立了包括温度、应力等变量在内的本构模型，描述了SMA的主要特性。Zhou［10］将SMA驱动器用于汽车自适应风扇离合器中，并推导了SMA驱动器的输出行程。Sun等［11］基于细观力学、不可逆热力学和对微结构物理机制的分析，解释了SMA在任意非比例加载下拟弹性和形状记忆特性的宏观现象及其细观机制。熊克等［12］研究了SMA丝缠绕角对扭力驱动器驱动性能的影响，得到了SMA扭力驱动器的力学模型，并对SMA扭力驱动器的响应速度进行了分析及实验研究。Peng等［13］采用混合物理论描述了SMA在非比例复杂热力加载条件下包括铁弹性、伪弹性、形状记忆特性在内的响应特性。陈松等［14］设计了一种MRF和SMA复合传动装置，在温度较低时依靠磁场控制的MRF来传递转矩，在温度升高、MRF性能下降时，利用SMA弹簧辅助传力对所设计的传动装置进行传力分析，推导了传动装置传力公式。

基于上述分析可知，国内外学者对单独的MRF和SMA材料及应用进行了大量研究，并取得了重要进展，但有关MRF和SMA联合作用的研究还比较少。本文在MRF和SMA联合作用方面进行了研究，针对热效应下SMA驱动的MRF和滑块复合传动，将MRF用于圆筒型传动，并考虑高温下SMA弹簧驱动的滑块产生的摩擦力以弥补MRF性能下降对传动性能的影响。

1 工作原理

图1为装置未工作状态示意图。其中：1为主动轴，2为电刷滑环，3为导线，4为导线孔，5为毛毡圈，6为SMA温控开关，7为储油腔端盖，8为SMA驱动位移弹簧，9为注液螺塞，10为储油腔，11为上壳体，12为MRF，13为励磁线圈，14为滑块，15为螺栓，16为导线孔，17为从动轴，18为右壳体，19为SMA压紧力弹簧，20为下壳体，21为左壳体，22为主动壳体。

图1 装置未工作状态示意图

工作原理及工作过程如下：

1）当主动轴1转动时，温度低于50℃，MRF储存在从动轴壳体的储油腔10中；当温度大于50℃时，SMA驱动位移弹簧8在热效应作用下轴向伸长，并随温度的升高而增大，逐步将MRF驱动进入主动圆筒和从动圆筒形成的工作间隙中；

2）温度低于70℃时，SMA温控开关6未给励磁线圈通电时，滑块14在离心力的作用下虽然能克服SMA压紧力弹簧19的拉力，但未与从动套筒内壁接触，只是间隙很小，传动处于分离状态。

3）当温度高于70℃时，SMA温控开关6开始给励磁线圈通电，磁通穿过工作间隙中的MRF，MRF中的磁性颗粒沿磁通方向排列成链状结构，从而增大了MRF的剪切屈服应力。同时，SMA压紧力弹簧19使滑块紧顶从动套筒内壁，依靠MRF的剪切屈服应力和滑块摩擦力的共同作用传递转矩，主动轴开始带动从动轴转动。随着温度的进一步升高，SMA温控开关上的滑片继续移动，使SMA开关内的电阻减小，励磁线圈中的电流增大，从而使产生的磁场强度增大，MRF传递的转矩增大。SMA弹簧压紧力增大，离心滑块传递的摩擦转矩增大，依靠MRF与滑块摩擦共同传递转矩，从而带动从动轴17转动，温度越高，转速越高。

4）当温度低于70℃时，SMA温控开关6断开励磁线圈的电流，磁场消失，SMA压紧力弹簧19及驱动位移弹簧8被收缩到原来状态，传动处于分离状态。在离心力和工作腔中压缩空气的作用下，MRF通过导管流回储油腔中保存起来，保持了MRF的性能，延长了MRF的寿命。本文中控制SMA材料的热量均来自装置自身产生的热量，使SMA材料在不同温度下分别行使闭合、驱动、挤压的作用。

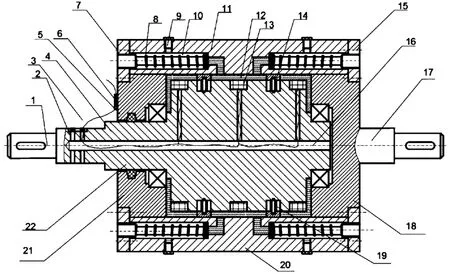
图2 装置工作状态示意图

2 MRF体积

2.1 MRF未工作时体积

MRF工作区域和储液区域简图见图3。当温度低于50℃时，形状记忆合金弹簧呈马氏体相，这时在储油腔中MRF的体积为

式中：V1表示储油腔中MRF体积；N为储油腔的个数；Δδ为SMA驱动位移弹簧的移动行程；A为活塞面积。

图3 关键几何尺寸示意图

2.2 MRF工作体积

当温度高于50℃时，SMA弹簧将产生奥氏体相变，表现为弹簧轴向伸长，从而将储油腔中的MRF推入工作间隙中。当温度达到70℃时，SMA弹簧完成奥氏体相变，这时储油腔中MRF全部被推进并充满传动装置的整个工作间隙，SMA弹簧轴向位移为［15］

式中：d1为弹簧丝径；D1为中径；n1为有效圈数；GL为低温切变弹性模量；γmax为最大剪切应变。G（T）为SMA弹簧的剪切模量，在相变区是温度T的函数，可表示为

式中：GM为SMA马氏体相的弹性模量；GA为SMA奥氏体相弹性模量；Tm＝（Af＋As）／2，ω＝π／（Af-As），其中As、Af分别为奥氏体相变开始和结束时温度。

工作时传动装置工作间隙中MRF的体积为

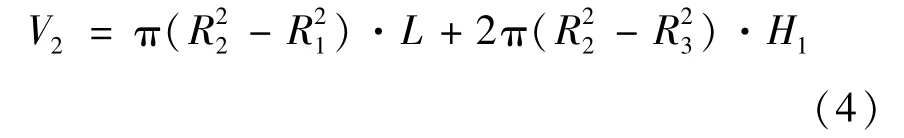
式中：H1为圆盘间隙；R3为圆盘小径；L为主动内圆筒的工作长度。

装置内导油孔中MRF的体积为

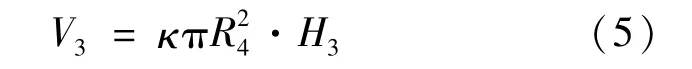
式中：V3表示装置内导油孔中MRF的体积；K为导油孔的个数；R4为导油孔的半径；H2、H3为导油孔的高度。因此，工作时装置中MRF的总体积为

3 传递转矩

3.1 MRF传动转矩

Sun等［16］针对温度对MRF的影响进行了实验研究。图4表明了实验中MRF材料MRM-1的实验所得的剪切应力τ与磁感应强度B的关系，最大剪切应力约为60 kPa，此时对应的磁感应强度约为9 kGs。将图4用Excel软件拟合，得到磁感应强度B小于9 kGs时的τ-B数学表达式为

在磁场作用下，MRF剪切应力可用Bingham模型［17］来描述，得剪切应力与磁感应强度的关系为

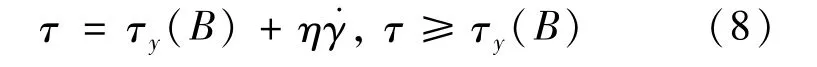
式中：τ为剪切应力；τy（B）为MRF的剪切屈服应力，它是磁感应强度B的函数；η为MRF零磁场时的黏度为剪应变率。

实验中，MRF材料MRM-1的零磁场黏度为0.1 Pa·s，剪切应变率为˙γ＝40（1／s），由式（7）（8）可得剪切屈服应力与磁感应强度的关系为

从图4可看出：剪切屈服应力随着磁感应强度的增加而迅速增大，当磁感应强度达到一定程度时，剪切屈服应力不再随磁感应强度的增加而增大，这是由于MRF中的磁性颗粒达到了磁饱和导致。

图4 剪切屈服应力与磁感应强度的关系

图5表示了MRF材料MRM-1的剪切应力与温度的关系［16］。最大剪切应力约为40 kPa，磁感应强度约为3.7 kGs，最小温度约为20℃，最大温度约为100℃。将图5用Excel软件拟合得到温度从20～100℃时的τ-T数学表达式为

图5 剪切应力与温度的关系

假设MRF的转矩为M，则MRF传递的转矩为M＝M1＋2M2，式中M1、M2分别为圆筒和圆盘的转矩，分别表示［16-17］为

3.2 摩擦滑块转矩

随着工况温度的升高，MRF受温度的影响传动性能下降，因此MRF传递的转矩会有所下降。当装置温度上升到一定程度，M f≤T≤Af时，此时SMA弹簧压紧力为［15］

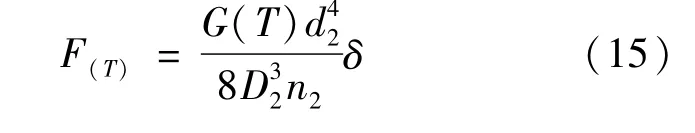
式中：d2为弹簧丝径；D2为弹簧中径；n2为有效圈数；δ为弹簧轴向伸缩量；G（T）为SMA弹簧的剪切模量，是温度T的函数。

在工作过程中，摩擦块在旋转作用下会产生离心力，也会产生离心摩擦转矩。假设由于离心力而使滑块产生的摩擦力为F1，总摩擦力为Ff，则

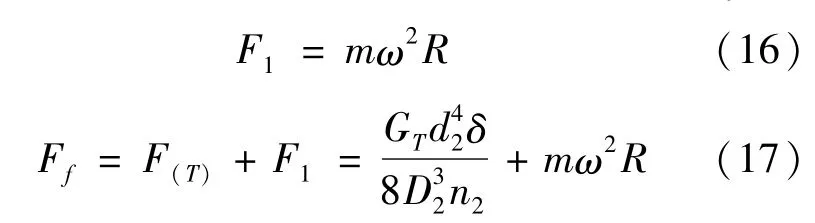
设摩擦滑块的转矩为M3，由式（17）可得摩擦滑块能传递的转矩为

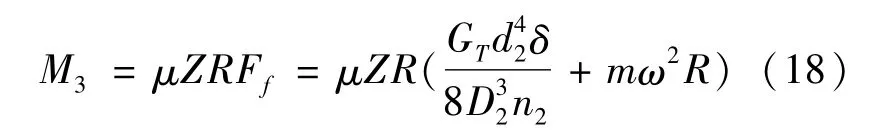
式中：μ为摩擦因数；Z为摩擦滑块的个数；m为摩擦块的质量；R为摩擦转矩的有效半径；ω为摩擦块的旋转角速度，由于摩擦块在主动内圆筒上，所以摩擦滑块的角速度与主动内圆筒的角速度相同。

综上，所述装置的总转矩M4为

4 结果分析与讨论

4.1 MRF体积

未工作时，MRF体积为V1＋V3，取MRF储油腔个数N为4，导油孔的个数K为8，导油孔的半径R4为1 mm，导油孔的高度H2＝H3＝5 mm，活塞的半径R＝9.56 mm，活塞的面积A＝288.276 mm2。由式（1）可得，V1＝21 567.04 mm3，故未工作时，MRF的体积为21 567.04 mm3。

本文中，SMA材料选为Ti-49.5at.%Ni，其结构参数和材料参数为：簧丝直径d1＝1mm，弹簧直径D1＝9 mm，弹簧匝数n1＝7，γmax＝1.5%，GL＝7.5 GPa，G＝25 GPa，As＝50℃，Af＝70℃，Ms＝40℃，M f＝20℃，Tm＝（Af＋As）／2，ω＝π／（Af-As），其中As、Af分别为奥氏体相变开始和结束时的温度。根据式（2）（3）可得SMA弹簧输出位移与温度的关系如图6所示。从图6中可以看出，当温度大于50℃时，SMA弹簧的驱动位移开始轴向伸长，并随温度的变化而变化，当温度分别为55℃、60℃、65℃、70℃时，弹簧的位移量分别为6.805、14.378、17.788、18.703 mm。当温度超过70℃时，驱动MRF进入主动圆筒和从动圆筒的工作间隙中，SMA弹簧的输出位移随温度的升高而伸长，当温度达到一定值时，SMA弹簧的驱动位移几乎不再伸长达到极限值，位移量约为18.703 mm。

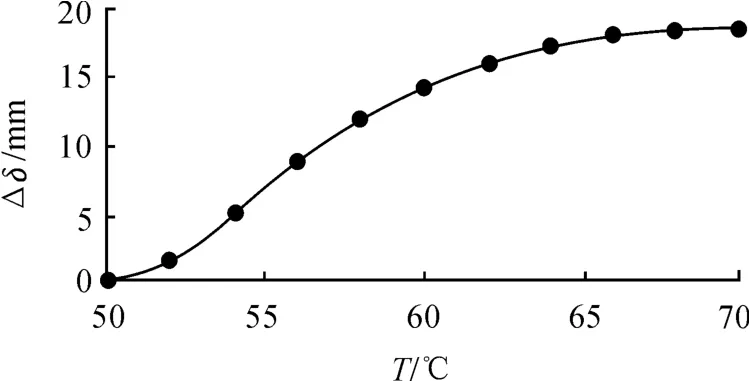
图6 SMA弹簧的位移变化与温度的关系

初始时MRF储存在储油腔中，由SMA弹簧推动进入工作间隙中的实际MRF体积与温度的关系如图7所示。当温度高于50℃时，SMA弹簧开始推动MRF进入工作间隙。当温度分别为55℃、60℃、65℃、70℃时，推入MRF到工作间隙中的体积分别为7846.758、16 590.027、20 511.281、21 567.035 mm3；当温度为70℃时，MRF充满整个工作间隙。

图7 MRF实际工作体积与温度的关系

工作时，MRF的体积为V＝V2＋V3，取R1＝34 mm，R2＝35 mm，L1＝L3＝30 mm，L2＝L4＝L5＝5 mm，L＝L1＋L2＋L3＋L4＋L5＝75 mm，圆盘间隙h＝1 mm，圆盘小径R3＝20 mm。由式（4）～（6）可得V＝21 520 mm3，考虑到安装以及加工制造过程中会产生误差，故未工作时MRF的体积略大于工作时的体积，从而保证了MRF能充满整个工作间隙。

4.2 MRF转矩

分析计算中，黏度为η＝0.1 Pa·s，剪应变率为＝40（1／S）。MRF传动的结构参数为：MRF工作间隙H1＝1 mm，导油孔高度H2＝H3＝5 mm，假定最大输入角速度为ωmax＝100 rad／s，得到转矩M与磁感应强度的关系和转矩M与温度的关系分别如图8、9所示。

图8 转矩与磁感应强度的关系

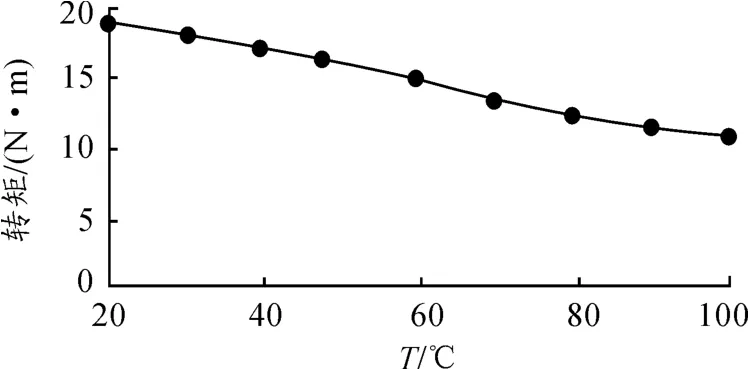
图9 MRF转矩与温度的关系

图8是当外加磁场作用时，如当磁感应强度B分别为0、2和4 KGs时，MRF传递的转矩分别为1.3149 7、15.444 7和25.226 9 N·m。当磁感应强度B达到9 kGs时，MRF基本达到磁饱和，其传递转矩为35.009 N·m。这表明随着磁感应强度的增加，MRF传递转矩的能力增大；当磁感应强度增加到一定值后，MRF达到磁饱和，MRF传递的转矩也达到极限值。图9是由方程（10）～（14）计算出的圆筒式MRF传动装置在外加磁场作用时传递转矩能力的计算结果。分析显示，温度从70℃升高到100℃的过程中MRF的转矩不断减小，表明温度对MRF的影响比较显著。

4.3 滑块摩擦转矩

本文中，SMA材料为Ti-49.8at.%Ni，其结构参数为：簧丝直径d2＝2 mm，弹簧直径D2＝14 mm，弹簧有效圈数n2＝6。相变温度为Ms＝40℃，M f＝20℃，As＝70℃，Af＝100℃。高温剪切模量GA＝25 GPa，低温剪切模量GM＝7.5 GPa。取恒定伸缩量δ＝8 mm，Tm＝（Af＋As）／2，ω＝π／（Af-As），其中As、Af分别为奥氏体相变开始和结束时的温度。根据式（15）可得SMA弹簧压紧力与温度的关系如图10所示。从图10可以看出：SMA弹簧的压紧力随温度的升高而增大，当温度达到一定程度时，SMA弹簧的压紧力基本不再变化，达到极限值，极限值约为24.295 N。

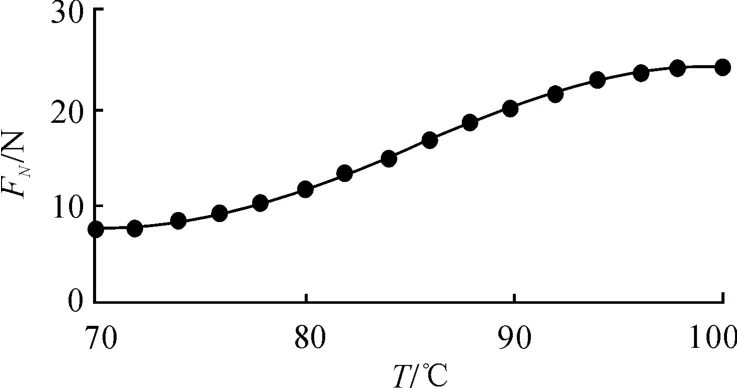
图10 弹簧压紧力与温度的关系

由式（16）～（18）可得滑块摩擦转矩与温度的关系如图11所示，式中摩擦因数μ＝0.1（在油润滑的条件下，钢的摩擦因数通常可取0.05～0.12），Z＝12，摩擦块的质量m＝0.2 kg，摩擦力矩有效作用半径R＝35 mm，摩擦滑块的角速度ω＝100 rad／s。从图11可以看出：当温度升高时。可通过摩擦滑块进行辅助传递转矩来补偿MRF在高温作用下传力性能下降的情况，提高了传动的稳定性。在SMA弹簧的作用下动摩擦块向外圆筒内壁方向贴紧产生摩擦，从而产生摩擦力矩，装置依靠这种摩擦力矩可在一定程度上补偿MRF因温度升高而传动性能下降的情况。

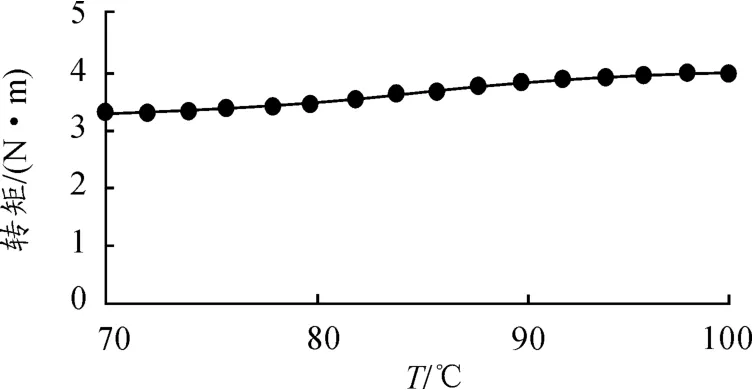
图11 摩擦滑块传递转矩与温度的关系

5 结束语

综合上述分析，由式（18）（19）可得到装置总转矩M4如图12所示。从图9可以看出，当温度升高时，MRF传递转矩能力下降；从图12可以看出，总装置传递的转矩虽然有小幅度的变化，但基本保持一致，从而保持了装置传动的稳定性，表明SMA驱动的MRF与滑块摩擦复合传动能有效弥补热效应下MRF传递转矩下降的情况。

图12 装置总转矩与温度的关系