基于盲源分离方法的声振降噪算法研究

卫 莹 南 林 杨德华 陈 涛

中国航天科技集团第四研究院401所 陕西 西安 710025

1 引言

振动与噪声测量是发动机状态监测与故障诊断的主要手段，研究和解决各种振动问题是当前工程技术领域的重要课题。在发动机试验中，振动源多，振动传播路径复杂，多种振动源信号与噪声以不同的方式混合在一起，使得观测信号成分十分复杂，进而影响特征信号的提取，给发动机性能监测与故障诊断带来困难，因此，需要研究固体发动机试验数据处理方法，对测量数据进行降噪处理，保证测量数据的可信度。我们将目标定位数据降噪——分离试验中的环境噪声。

现有的振动信号降噪方法有滤波，小波分析等方法，虽然可以满足固体火箭发动机试验使用要求，但传统的低通滤波会过分抑制噪声，使得信号失真，高通滤波会使得背景噪声同时加强，不符合固体发动机试验中对数据的准确性、可靠性、误差小的要求，并且固发试验中的振动信号具有突变性特征，现有方法常为针对平稳段信号的降噪处理方法，不符合固体火箭发动机试验振动信号特性。

本文通过设计适应固体发动机试验环境下的FastICA-AIC新算法，进行振源信号与噪声信号的分离，将其应用在其它不同型号发动机上，均进行了有效的信号分离，证明将此方法应用到我们固体火箭发动机测试中，可以更有效的进行发动机状态诊断与监测，对提升测试技术有较大的帮助。

2 快速振动信号分离方法的数学模型与FastICA-AIC算法实现

对采集到的振动源信号，先进行AIC算法的源信号个数判断，其输出(源信号个数k)作为下一步信号分离算法的输入参数之一；根据预判得到的源信号个数k，用改进的FastICA算法——少分多FastICA-AIC分离与改进的学习函数——正弦函数sin(x)运算，对采集到的振动源信号进行信号分离，得出分离结果。

BSS问题包含两层含义:源数估计和源分离，源数的确定是盲源分离问题的关键点，是盲源分离实施之前的重要步骤，也是本文着重解决的一个问题，结合发动机试验的特定环境，源信号的个数无法人为判定的情况，基于AIC判别准则，结合ICA算法，建立模型，设计FastICA-AIC新算法。

信号均方误差(SMSE)公式如下:

时延相关系数(DDCC)公式如下:

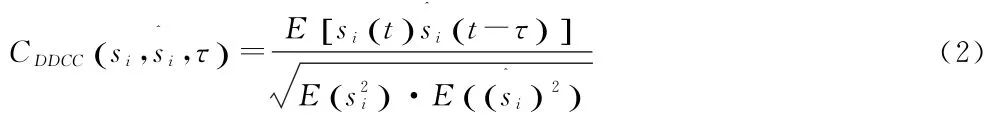
其中:sk为源信号为相应的估计信号，K为源信号个数，τ为时延值。

因为结合发动机试验的特定环境，源的种类较多且源信号的个数无法判定，源信号的个数与噪声源个数相关，设源信号的个数为k，通过模型选择来调整预设参数，运用AIC判别准则完成源信号个数识别。AIC标准在模型的复杂度和此模型拟合数据的优良性权衡上有充分考虑，故我们采用AIC标准选择源信号的个数k。AIC判别准则是基于特征值根据信息论准则确定的源数估计方法。Akaike信息论准则(AIC)通过最小化如下代价函数选择模型

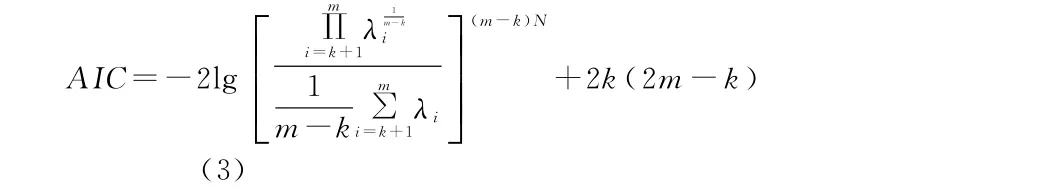
其中，λi为观测信号的特征值，N为样本数，当k从1到m取值时，最小的AIC(k)所对应的即为信号子空间维数n，即信号的源数估计。

2.1 Fast ICA分离算法改进研究——少分多Fast ICA-AIC分离算法

上文所述的Fast ICA分离算法是从N个源信号分离出N个信号，但在发动机实际应用中，采集到的一路观测信号即为混合信号，包含多种源信号，所以我们需要提出一种少分多的Fast ICA-AIC分离算法，使得其符合固发试验数据的实际情况，更加具有实用性。

通过改进ICA算法，将矩阵维数由M*M维改为M*k，从而实现对采集到的M路源信号分离出N个独立信号(其中M＜N)。

图1是3个源信号，由该组源信号混合产生的4路混合信号如图2所示，经过改进

算法实现的少分多结果如图3所示。通过直观的时域信号波形就可以清楚看出，该改进算法的分离效果很好，能够清晰的辨别出图1所示的源信号。

图1 搭载试验平台采集到的源信号

图2 根据搭载试验平台采集到的源信号随机混合后的四路混合信号

2.2 快速振动信号分离方法的数学模型 经过算法分析和实际试验验证，建立了振动信号快速盲分离的数学模型，如公式(4)所示。

对采集到的振动源信号，先进行AIC算法的源信号个数判断，其输出(源信号个数k)作为下一步信号分离算法的输入参数之一；根据预判得到的源信号个数k，用改进的Fast ICA算法——少分多Fast ICA-AIC分离与改进的学习函数——正弦函数sin(x)运算，对采集到的振动源信号进行信号分离，得出分离结果。

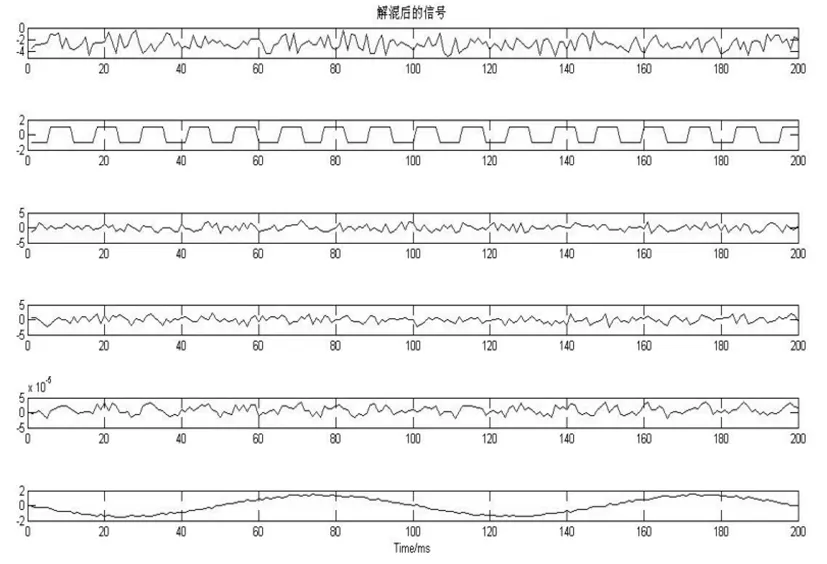
图3 根据改进Fast ICA算法解混后的分离信号

2.2.1 算法FastICA-AIC过程与软件实现

1)对采集到的各路振动源信号进行EMD分解，得到源信号的本征模函数mi；

2)各路源信号的本征模函数复合构成一组新的本征模函数M，并对本征模函数M的相关阵进行特征值分解(SVD分解)，得到特征值向量；

3)消除特征值为0的元素，组成新的长度为L的特征值向量；

5)确定AIC的最小值，其对应的k即为源信号的数目N；

6)对观测数据X进行中心化，使它的均值为0；1

7)对数据进行白化，X→Z；

8)选择需要估计的分量的个数m，设迭代次数p←1；

9)选择一个初始权矢量(随机的)WM×k；

10)令WM×k=E{ Z sin()}-E{ sin'()}W，非线性函数g的选取见前文；

11)WM×k=WM×k-( WpTWj)Wj；

12)令WM×k=WM×k/‖WM×k‖；

13)假如WM×k不收敛的话，返回第5步。即振动信号快速盲分离的算法迭代公式为

Z为观测数据X白化后的矩阵，WM×k为权矢量，WM×k=WM×k/‖WM×k‖。

3 发动机试验

我们将本文提出的FastICA-AIC算法应用至固发试验中，验证其在试验中应用的可行性。搭载振动传感器与噪声传感器进行某型号固体火箭发动机地面试验。

3.1 AIC准则源数的判定 在实验室激振器上安装标准振动传感器，在激振器工作的过程中，对标准振动传感器附加外部冲击激励，通过标准振动传感器采集到的振动数据仅包含了确定已知的两个激励源信号，运用AIC算法对采集到的振动数据进行处理得到的AIC输出结果为:AIC=[4.2947，0.0087，0.0098，0.0105，0.0115，0.0122，0.0126]，结果表明在第2个数据点[0.0087]出现最小值，根据AIC算法的判定准则，使得AIC值最小的个数即为源信号个数，即该信号包含有两个独立源信号，与实际情况一致。

3.2 发动机试验过程

3.2.1 试验准备 本次试验选用振动与噪声传感器，为了物理消减发动机工作噪声对振动信号的影响，我们对使用的部分振动传感器进行了防护，防护方法包括包裹耐火泥块和包裹南大胶。

从图4空置振动传感器信号可以看出，即将振动传感器远离发动机，只感受点火冲击波与环境噪声所带来的振动，发现幅值在±10g，表明环境噪声确实会对振动信号造成干扰。图5为振动传感器包裹耐火泥块、南大胶时的时域振动信号，表明经过物理防护，隔绝掉部分干扰后，幅值有一定程度的降低，再次证明环境噪声会对振动信号造成干扰。

本次试验共在发动机上选择了五个测点位置，第一测点和第二测点在前裙，这两个测点位置为90°对称；第三测点和第四测点在筒段中部，这两个测点位置也为90°对称；安装这四个测点的振动传感器时，安装块紧贴发动机表面；第五测点只安装一路噪声传感器且安装方向面向振动源，使它远离测试架和发动机。

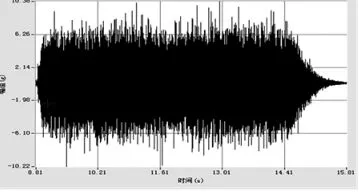
图4 发动机试验中空置振动传感器信号

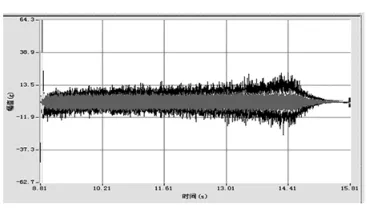
图5 发动机试验中振动传感器包裹耐火泥块、南大胶时的时域振动信号

图6 发动机试验中第2和第4测点

图7 发动机试验中第3测点与第5测点

3.2.2 试验结果分析 试验数据分两部分进行分析。

第一部分为第一测点的4只传感器信号，采用FastICA-AIC算法进行分离，分离前后的时域信号如图8所示，分离前后的频域信号如图9和图10所示，分离前后的功率谱如图11和图12所示。前三路信号分别为振动传感器时域信号、耐火泥块防护的振动传感器时域信号和南大胶防护的振动传感器时域信号，最后一路为噪声传感器时域信号。

通过比较同一频率成分下幅值的变化情况和有无新的频率成分产生，可以判断工况情况。从采集信号频谱图和分离信号的频谱图对比可以看出，图9(4)中的噪声信号频谱与图10(2)中频谱信号从主频成分到最大值所对应的频率均一致，且各个频率分布一致，集中在400 Hz与660 Hz，图9(2)和图10(3)中的振动信号频谱与图10(3)中频谱信号基本一致。

从采集信号功率谱和分离信号功率谱对比可以看出，图11(4)中的噪声信号功率谱与图12(1)中功率谱信号基本一致，图11(2)和图11(3)中的振动信号功率谱与图12(2)中功率谱信号基本一致。表明通过Fast ICA-AIC算法，可以有效的将环境噪声信号进行分离。

第二部分为第一和第二测点的共8只振动传感器信号，前6路为振动信号，后2路为噪声信号，分离前后的时域信号如图13所示，分离前后的频域信号如图14和15所示，分离前后的功率谱如图16和17所示。

从采集信号频谱图和分离信号的频谱图对比可以看出，图14(1)中的噪声信号频谱与图15(2)中频谱信号基本一致，图14(2))中的振动信号频谱与图15(3)中频谱信号基本一致。其中，图15(1)中的主频成分为50 Hz的整数倍，与工频干扰一致。从采集信号功率谱和分离信号功率谱对比可以看出，图16(1)中的噪声信号功率谱与图17(2)中频谱信号基本一致，图16(2)中的振动信号功率谱与图17(3)中频谱信号基本一致。FastICA-AIC算法进行分离，分离前后的时域信号如图8所示，分离前后的频域信号如图9和图10所示，分离前后的功率谱如图11和图12所示。

图8

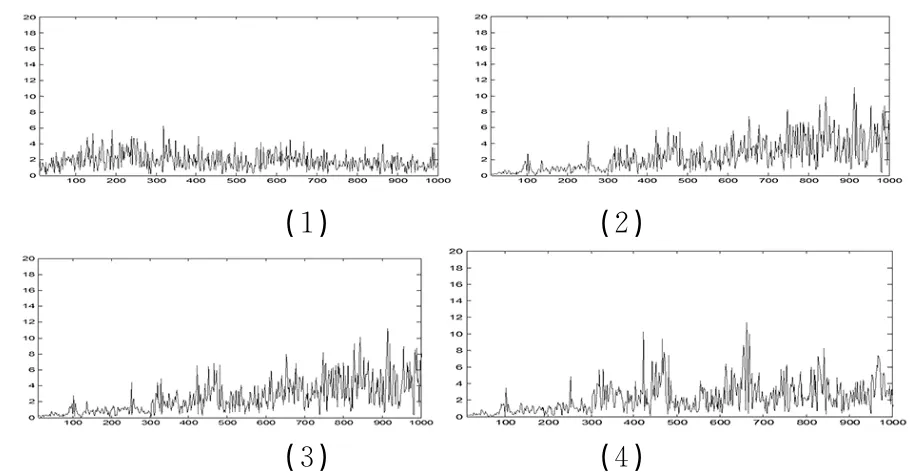
图9

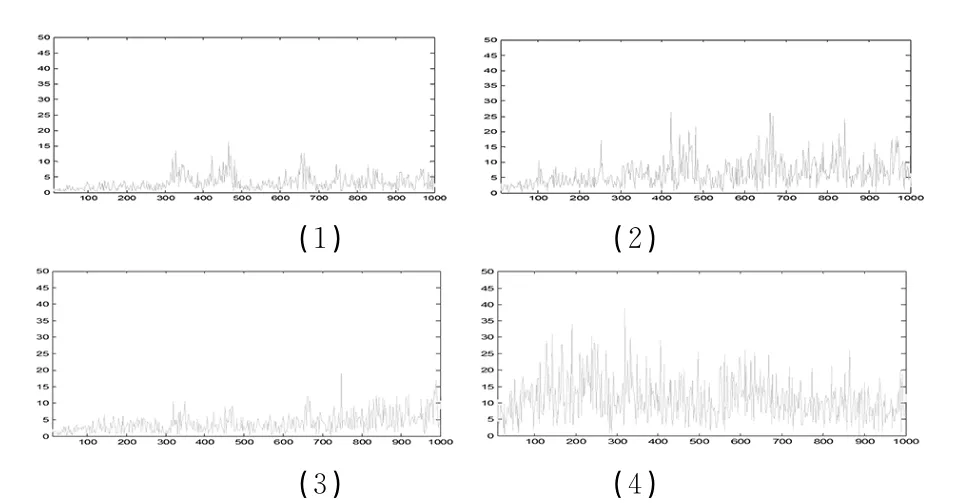
图10

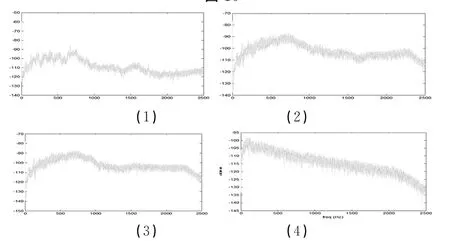
图11

图13

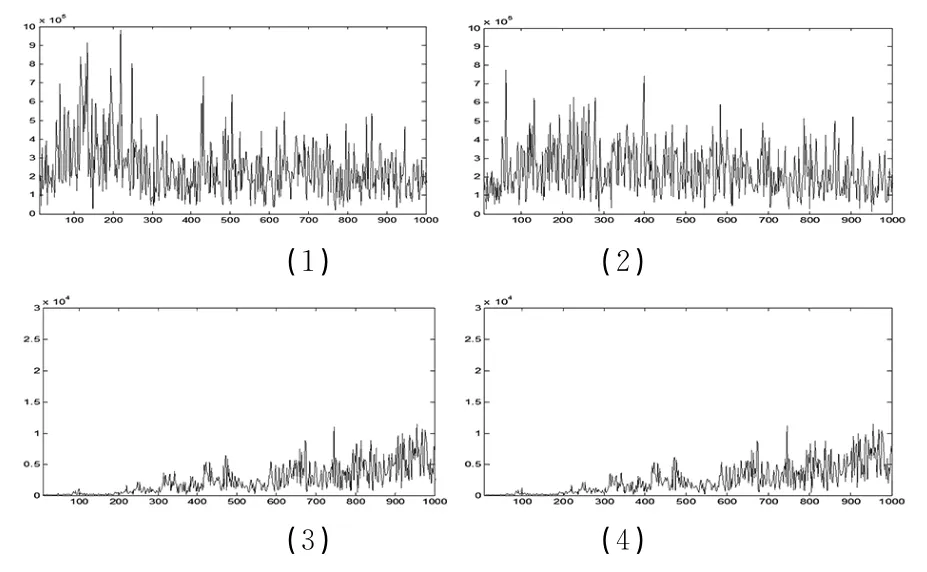
图14

图15

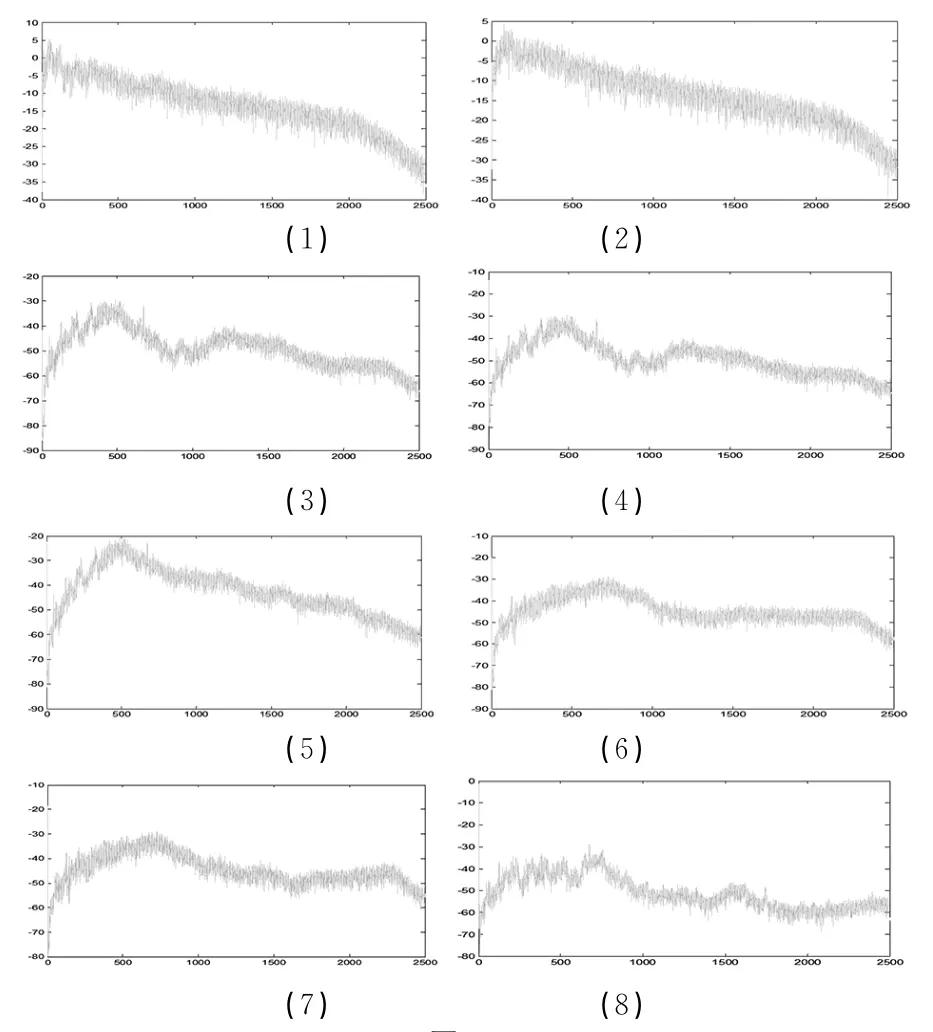
图16

图13-17:选取第二部分为第一和第二测点的共8只振动传感器信号，前6路为振动信号，后2路为噪声信号，采用Fast ICA-AIC算法进行分离，分离前后的时域信号如图13所示，分离前后的频域信号如图14和15所示，分离前后的功率谱如图16和17所示。

图17

3 总结

本文设计ICA方法与源信号个数识别的新算法-快速振动信号分离算法Fast ICA-AIC，实现“以少分多”，即对采集到的M路源信号分离出N个独立信号(其中M＜N)；将FastICA-AIC算法应用在固体发动机试验中，解决环境和设备较为复杂情况下的发动机振动源信号辨识和噪声分离问题，结合试验数据，分析振源信号的分布特性。