金属结构环境累积损伤研究进展

钟勇，苏艳，滕俊鹏，王强，李祖柳，肖桂琴

（1.西南技术工程研究所，重庆400039；2.成都飞机设计研究所，成都 610091）

金属结构在使用过程中总是暴露于一定的环境中，不管是外界自然环境，还是内部微气候环境都会对金属结构材料产生持续的腐蚀作用，导致点蚀、晶间腐蚀、微观裂纹等各种腐蚀损伤。环境腐蚀是一种慢作用渐进过程，短时间内对金属结构的影响轻微，往往需要历经数月到数年，当腐蚀损伤累积到一定量值，才会造成结构性能明显下降，或功能丧失。然而，当结构件处于工作状态时，环境因素和工况载荷的联合作用将引起结构突然断裂或提前破坏。调查发现，这种突发性破坏在桥梁等工程结构，以及航空、兵器等装备承力结构中都发生过，轻则影响使用，重则发生灾难性事故。为了保证金属结构的安全可靠，环境腐蚀与工况载荷的协同作用已成为结构设计必须考虑的重要因素。

数十年来，国内外学者从金属结构环境损伤影响因素、环境损伤演变规律、环境及力学耦合机理等多个方面对金属材料及结构开展了大量的研究工作。这些研究工作在金属结构累积损伤理论研究、模型构建以及工程应用上取得了一定成果，但由于环境与力学耦合机制极其复杂，对结构损伤的影响规律尚不清楚，现有累积损伤理论主要考虑单纯机械载荷作用，如线性疲劳累积损伤理论、非线性疲劳累积损伤理论等，同时考虑环境作用的累积损伤理论较少。

文中简要介绍了金属结构环境损伤的主要影响因素，对当前国内外金属结构累积损伤理论与模型进行了系统梳理，重点探讨了金属结构环境累积损伤研究未来发展方向。

1 金属结构环境损伤的影响因素

金属材料/结构在各种内外部因素（包括组织成分、热处理状态、结构形状、加工工艺、力、温度、 腐蚀、辐射等）作用下出现宏观上的损伤，这一过程从本质上看，可以理解为金属材料内部受外界因素影响产生微观缺陷（如微裂纹和微孔洞），这些缺陷的形核、扩展、汇合最终造成材料的逐渐劣化，直至破坏[1]。具体而言，金属结构的环境损伤通常主要表现为两类：由环境腐蚀作用或环境-载荷耦合作用造成的缺陷，如点蚀坑、应力腐蚀（微）裂纹、腐蚀疲劳（微）裂纹等；由各种内外应力单独作用造成的损伤，如外加载荷对材料/结构静强度、疲劳寿命等产生影响，以至结构出现裂纹、断裂、失效等。

金属结构环境损伤的影响因素十分复杂，国内外学者针对各种影响因素进行了大量的理论机制、规律模型等研究，此处不再论述。金属结构环境损伤的主要影响因素见表1[2]。

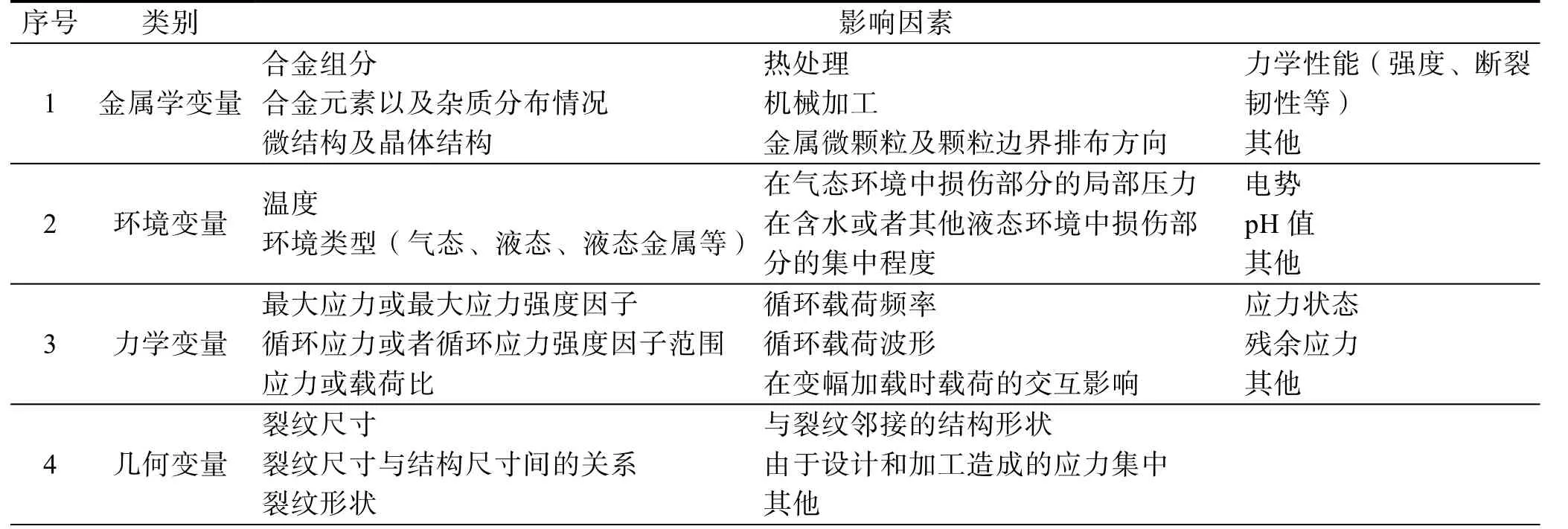
表1 金属结构环境损伤的主要影响因素

2 金属结构累积损伤理论与模型简介

2.1 概述

由前述金属结构环境损伤影响因素分析可知，当金属结构在金属学和几何上的各种变量/参数完全确定后，对金属结构损伤影响最大的就是力学载荷和环境带来的影响，而环境对金属结构的影响又往往以腐蚀为主。基于上述认识，金属累积损伤领域围绕这些影响因素研究发展至今，涌现出了一大批颇具代表性的理论与模型。这些理论按照是否考虑环境腐蚀影响，可以简单分为两类：不考虑环境腐蚀影响的金属累积损伤理论与模型（主要包括传统的Miner线性累积损伤理论、其他非线性累积损伤理论等）和考虑环境腐蚀影响的金属累积损伤理论与模型（包括预腐蚀疲劳模型、腐蚀疲劳模型等）。

2.2 不考虑环境腐蚀影响的金属累积损伤理论与模型

2.2.1 线性累积损伤理论（Miner理论）

Miner理论[3-9]中假设损伤积累与疲劳次数成线性关系，在1945年时将此理论公式化，形成了著名的Miner法则，即Miner线性累积损伤法则。此法则形式简单，易于使用，在工程实际中得到了广泛应用。在该理论中，假设各个应力之间相互独立、互不相关，因此疲劳损伤可以按线性累加，而当累加的损伤达到某一程度（数值）时，疲劳破坏就会发生。

l）一个载荷循环造成的损伤：

式中：N为对应当前载荷水平下的疲劳寿命。

2）n个等幅载荷循环造成的损伤：

变幅载荷下，造成的损伤：

式中：Ni为在应力si下的疲劳极限寿命。

3）当累计损伤D等于临界疲劳损伤DCR且等于1时，产生破坏。

Miner理论提出后，被广泛应用，经过大量实践证明，Miner法则的预测结果与实测数据之间通常存在较大差异，且材料或试件在发生失效破坏时所累积的损伤总量并不一定为1，通常在0.01～10的较大范围内波动[10-12]。这是因为Miner 法则的假设中，各级载荷相互独立，损伤累积与加载历程无关，没有考虑载荷加载顺序、载荷相互作用效应的影响，从而导致其寿命预测偏差较大。在文献[4]中推导了二级载荷加载下材料破坏时累计损伤D与1的关系，载荷加载顺序为高-低加载时，累计损伤D＜1；载荷加载顺序为低-高加载时，累计损伤D＞1。因此提出修正Miner理论，即当累计损伤D等于临界疲劳损伤DCR等于a时，产生破坏。a值因材料而异，而且随载荷谱和加载水平改变，在确定材料和加载条件下a为常数。

2.2.2 Marco-Starkey理论

针对Miner 法则的固有缺陷，许多学者通过改变损伤的积累形式，研究提出了非线性损伤累积理论。Richart和Newmark最早提出损伤曲线的概念。据此，Marco和Starkey[13]通过载荷顺序加载试验，提出了一种考虑载荷水平的损伤曲线模型，即Marco-Starkey非线性累积损伤理论，该理论将损伤定义为：

式中：n为对应载荷下的循环次数；N为对应载荷下的极限循环次数。Ci（Ci＞1）由试验确定，是与应力水平相关的常数。该理论假设：损伤与载荷顺序无关，当损伤D=1时发生疲劳破坏。该理论的不足之处为Ci未给出具体定义，很难被赋值。

2.2.3 Manson-Halford理论

前述Marco-Starkey理论未给出损伤指数的具体形式，在实际应用时仍存在一些问题。此后，Manson和Halford[14]在“有效裂纹增长模型”基础上发展并完善了Marco-Starkey理论，定义损伤为瞬时裂纹长度与最终裂纹长度之比。

Manson-Halford提出裂纹的扩展方程为：

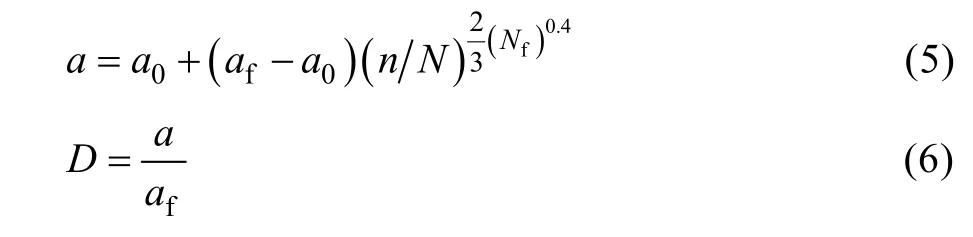
式中：a0为初始疲劳导致的裂纹长度；n为加载次数；af为外加载荷的疲劳寿命为Nf时的裂纹长度。

经过一系列数学推导得出，在两级载荷下破坏时，Manson经验公式为：

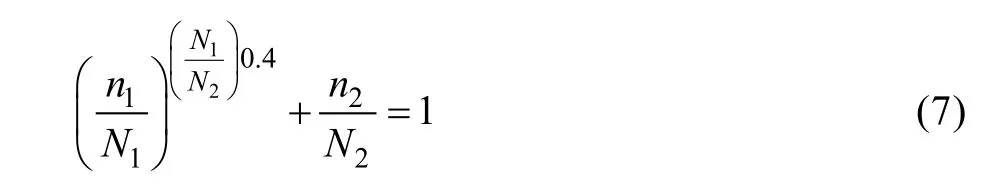
式中：Ni是对应于当前载荷水平的疲劳寿命；ni为对应疲劳次数。

此类模型与两级载荷试验结果吻合较好，但并没有证明适用于多级或随机载荷。另外该模型同样没有考虑载荷间的相互作用效应。

2.2.4 Corten-Dolan理论

Corten-Dolan理论[15]认为，材料的疲劳损伤实质是裂纹的累积与联合，它与材料损伤核数目和裂纹扩展速率有关。该理论认为等幅载荷下n个循环造成的损伤为：

式中：n为循环次数；m为损伤核数目（应力越大，m越大）；r为损伤发展速率（正比于应力水平）；c、d为材料常数。

经过一系列数学推导，最终得出多级加载情况下的Corten-Dolan公式为：

式中：Nf为多级交变应力下破坏总循环数；σ1为多级交变应力中的最大交变应力；N1为σ1下破坏循环数；σi为第i级交变应力；λi为σi下的循环百分数，即λi=ni/Nf；d为材料常数（由试验确定）。

此理论的不足之处在于部分假设与试验事实不符，而且给出的损伤公式形式复杂，损伤核数目等参数难以确定，公式的实用意义不大。

2.2.5 叶笃毅模型

叶笃毅[16-17]选择韧性作为疲劳损伤表征的力学参量，从交变载荷下材料的韧性耗散规律出发，结合对疲劳损伤的能耗过程分析，系统研究并提出了疲劳损伤变量、损伤临界值、损伤演化方程和累积损伤模型。据此建立了一种新的疲劳损伤定量方法——韧性随疲劳损伤演化的耗散模型，并在实验中得到了验证。

通过一系列数学推导，最终得出在第二级应力σ2作用下的剩余循环比：

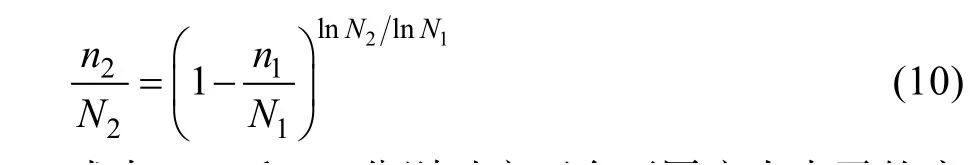
式中：N1和N2分别对应两个不同应力水平的疲劳断裂周次；n1和n2分别对应两个不同应力水平的疲劳次数。

该模型的优点是形式简单，具有较好的物理基础，不需要其他试验常数。在最后的损伤表达式中，只含循环数n这一个参量，不含其他力学参量，本质上是另一种形式的幂指数模型。

2.2.6 胡明敏模型

胡明敏[18]同样以材料静力韧性为宏观损伤变量，依据疲劳过程中金属材料韧性随疲劳循环加载而变化的实验结果的规律分析，得到了应力和循环数表达的损伤演化方程和损伤累积模型。

该模型从剩余静力韧性模型出发：

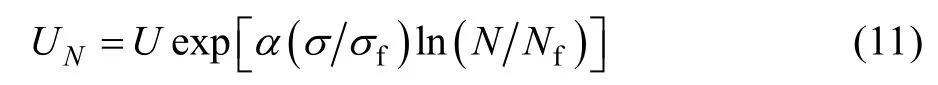
通过数学推导得出，材料二级加载断裂时：

通过式（12）可以计算二级应力加载情况下材料剩余疲劳寿命。

2.2.7 其他模型

前述理论与模型主要聚焦于材料/结构在疲劳载荷作用下对其疲劳寿命的影响。在外加载荷作用下，金属结构除了发生疲劳损伤外，其剩余强度等静力性能指标也可能发生变化，为此一些研究人员对其损伤理论与模型进行了专门的研究。文中简要介绍其中两个比较有代表性的模型。

1）敖波模型。敖波[19]在Schaff提出的剩余强度模型基础上，提出了等损伤比剩余强度模型，给出了多级载荷作用下剩余强度的退化模型公式，并用于多级载荷作用下剩余强度的估算。

由Schaff提出的剩余强度模型，推导得出载荷S1经历n1次循环后的剩余强度R(n1)为：

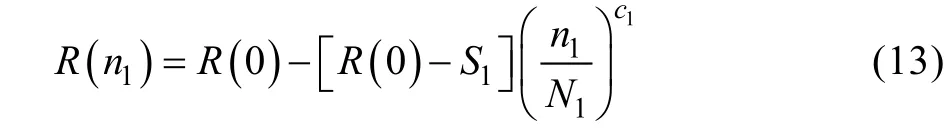
式中：R(0)为初始强度；N1为载荷S1下直至破坏的循环数；c1为常数。

两级载荷作用后的剩余强度为：

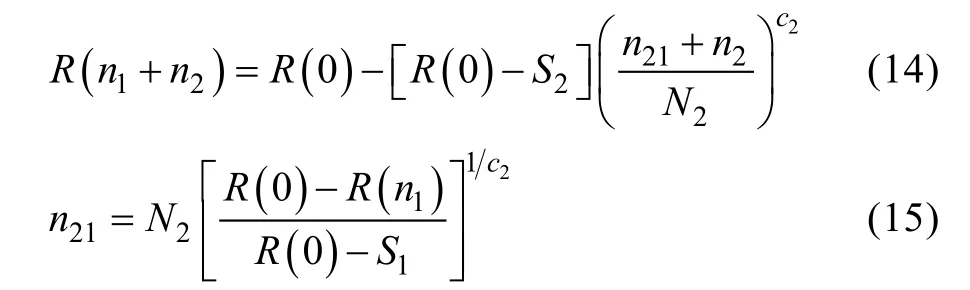
式中：R(0)为初始强度；N2为载荷S2下直至破坏的循环数；c2为常数。通过该模型可预估剩余强度，但确定c1、c2数值较困难。

在这里，除了路面、建筑物、少量的麦地和玉米地外，其他地方几乎都被草地所覆盖。铺天盖地般舒展开来的绿野为荷兰奶牛提供了充足的食物，新鲜的青草，换来的是新鲜的牛奶，最后便是奶酪了。这里的奶酪品种之全，让人叹为观止。

2）苏志霄模型。苏志霄[20]通过对正火45钢的试验数据分析，给出了对称恒幅应力循环下疲劳损伤的定义，提出了一个反映剩余强度退化的对数表达式。该表达式能够反映损伤演化的非线性特性。

材料在应力下经历n个循环后剩余强度表达式为：

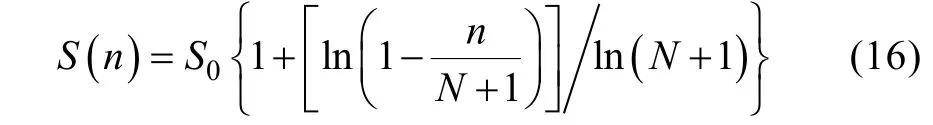
式中：n为对应应力下循环次数；N为对应应力下极限循环次数；S0为材料初始强度。

2.3 考虑环境腐蚀影响的金属累积损伤理论与模型

金属材料/结构暴露于环境中时，受各种环境因素影响，容易出现腐蚀现象。由于金属腐蚀本身具有很大的不确定性，加之腐蚀与力学载荷的耦合复杂多变，给腐蚀环境下的金属累积损伤分析带来了非常大的难度。在大量的研究基础上，一些学者提出了一种逻辑上比较简便直观的思路——将环境腐蚀的影响以某一系数或某种数学上的关联关系引入已有的金属累积损伤理论与模型中，充分借助现有的累积损伤理论与模型，实现结构损伤与寿命预测。在这一思路下催生了很多相关理论与方法[21]，如基于S-N曲线的材料预腐蚀影响系数法（C系数法）和腐蚀条件下细节疲劳额定值方法（DCR法）、基于ε-N曲线的局部应力应变法、基于断裂力学方法的腐蚀改进等效初始裂纹尺寸方法（CM-EIFS法）、将腐蚀与疲劳裂纹扩展结合的分析模型、将电化学与断裂力学结合的模型等。

2.3.1 预腐蚀疲劳裂纹扩展分析模型

贺小帆等[22]认为在耐久性分析中的相对小裂纹范围内，预腐蚀T时间后，相对小裂纹扩展规律仍可以采用类似于断裂力学中描述裂纹扩展的Paris公式的形式，对室温大气环境下相对小裂纹扩展公式进行修正：

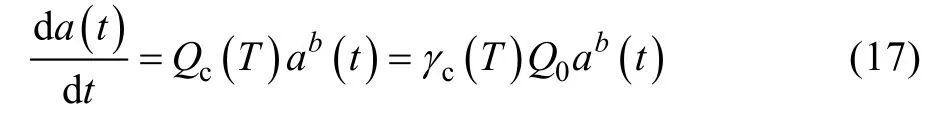
式中：t为指定使用寿命；a(t)为与t对应的裂纹尺寸；Q0为室温大气环境下的裂纹扩展速率；Qc(T)为腐蚀环境下腐蚀时间T对应的裂纹扩展率，Qc(T)=γc(T)Q0；γc(T)为裂纹扩展率的腐蚀修正系数，γc(T)=Qc(T)/Q0，在耐久性分析的相对小裂纹扩展阶段，b=1。

事实上，当预腐蚀时间确定后，γc(T)为常数，则式（17）为：

必须指出，预腐蚀裂纹扩展模型不适用于腐蚀和疲劳同时发生的情况，仅适用于疲劳和腐蚀交替发生的情况。

2.3.2 腐蚀疲劳裂纹扩展分析模型

在前述预腐蚀疲劳裂纹扩展分析模型基础上，贺小帆[22]等进一步研究了腐蚀环境下的裂纹扩展速率模型，认为仍可沿用一般环境下的相对小裂纹扩展速率公式，只需在适当的参数中考虑腐蚀的影响，即引入腐蚀修正系数。这是一种通用的工程简化处理方法，并给出了通常条件下的确定性裂纹扩展方程（见式（17））。

在材料、结构形式以及载荷谱确定后，Qc(T)、γc(T)均为应力水平和腐蚀时间的函数。腐蚀疲劳与预腐蚀疲劳的区别在于，腐蚀环境下的修正系数γc在腐蚀疲劳中始终为随时间的变量，而预腐蚀时间给定后，该系数则为常数。腐蚀疲劳裂纹扩展模型适用于分析腐蚀环境下的疲劳问题。

2.3.3 电化学分析与断裂力学结合的分析模型

结构在使用中，往往同时承受环境腐蚀作用和载荷作用，当载荷为疲劳载荷时，结构损伤扩展包括腐蚀损伤扩展和疲劳损伤扩展两部分。电化学分析与断裂力学结合的分析模型中，通常假定两者相互独立。首先依据电化学原理建立腐蚀速率模型、腐蚀深度等模型（很多学者对腐蚀速率、腐蚀深度等参数随时间变化的数学表达进行了大量的研究，建立了多种多样的模型[1,23]）。之后，依据断裂力学中疲劳裂纹扩展模型，对比腐蚀损伤扩展速率和疲劳裂纹扩展速率，实现腐蚀深度、腐蚀率、时间与剩余寿命等参数的串联。

将电化学腐蚀与断裂力学结合用于分析结构损伤是一种很有意义的尝试。初步的研究表明，该模型适用于分析单一的金属，对复杂连接结构以及含表面氧化工艺的结构并不适用，同时该方法仍有待进一步试验验证。

2.3.4 其他结构寿命评定模型

除以上模型以外，还有一些研究人员针对环境腐蚀影响下的金属结构提出了不同的剩余寿命预测方法与模型：如通过有限元软件建立预腐蚀试验件的有限元模型[2]，从而预测结构寿命；将结构使用过程简化为腐蚀和腐蚀疲劳的两个弱相关过程，引入综合反映上述作用的腐蚀影响系数k(T)（k随环境、时间（t）变化）预测结构疲劳寿命[24]；采用BP神经网络模型将复杂环境和载荷交替的复杂影响规律简化为数学模型，以腐蚀参量为输入层，疲劳寿命的累积衰减率为网络输出层，借助训练后的模型预测结构寿命[25]等。

3 结语

金属材料/结构自加工制造成型后，在实际使用中受腐蚀环境、力学载荷等因素作用不可避免地会产生损伤，这是客观规律。研究金属材料/结构环境累积损伤规律与机制，对于金属材料/结构的正常使用、寿命预测等具有重要意义。

由于金属环境损伤影响因素众多，当研究对象由简单材料件上升到结构件层级时，不同于材料件受环境或载荷单独作用造成的单一类型损伤，外部环境、结构细节、受力形式等多方面因素的耦合，往往导致金属结构的损伤机理发生明显变化，其损伤类型/模式、损伤规律更加复杂。特别是环境-载荷耦合方式的复杂多变，给环境-载荷耦合作用下金属宏微观损伤研究带来很大难度。如何表征环境-载荷耦合作用下金属结构的损伤，掌握损伤机理，并构建合适的理论与模型，准确评价预测结构损伤，一直是该领域的研究热点与难点。

现阶段，以金属材料件在环境、载荷单独作用下的损伤研究为切入点，逐步上升到含孔件、装配件、连接结构等不同结构形式。同时对环境变量的影响（尤其是综合影响）进行细化研究，通过多层级“积木式”研究建立环境（腐蚀）损伤参量-力学性能退化关联模型，是解决金属结构环境-载荷耦合作用下损伤演变规律与机理、剩余强度/寿命评价与预测等关键问题的有效路径。