山区单悬臂廊桥结构抖振响应及等效风荷载

苏 益 ，李明水 ，杨 阳 ，段青松

（1. 西南交通大学土木工程学院，四川 成都 610031；2. 西南交通大学风工程四川省重点实验室，四川 成都610031）

抖振是紊流作用引起的结构随机振动，以紊流中脉动部分引起的结构强迫振动为主，一般不会引起灾难性破坏，但会导致结构的功能性障碍，且在任意风速下均可发生. 对于桥梁结构而言，过大的抖振会危及结构安全、影响行人及车辆舒适度、缩短部分构件疲劳寿命等. 随着人们对桥梁风工程深入研究发现，风敏感的桥梁结构不仅限于大跨度桥梁，很多短、中跨桥梁结构也被归为风敏感结构中，如某些人行桥梁等[1]. 近年来更有多座山区悬挑式观景廊桥出现，诸如科罗拉多U型廊桥、重庆云阳廊桥、重庆万盛廊桥等，且悬挑长度不断增大. 目前山区桥梁抗风大都针对悬索桥及斜拉桥等大跨度桥梁[2-3]，此类悬挑式廊桥的抗风问题研究极少. 并且由于山区风环境的复杂性，尚无法利用规范获得设计参数，需通过风洞试验等手段进行研究.

山区地形复杂，局部风环境影响因素多，深入研究桥位风环境是山区桥梁抗风设计的前提[4-6]. 山区各类风场特性参数对结构三分力系数及抖振响应均有影响[7]. 文献[8]中就风场参数的不确定性对风振响应的影响做过研究，并给出相应结论. 河南新乡南太行关山一号拉索观景廊桥建于海拔1 533 m悬崖边缘，悬挑长度70 m，设计风速48 m/s. 本文以该廊桥结构为背景，针对各风场特性进行风洞试验，根据试验结果分析各参数对结构三分力及抖振响应的影响，并给出结构等效静力风荷载，为山区风环境下类似长悬挑结构的抗风设计与研究提供参考.

1 试验概况

1.1 试验设备及模型

试验在西南交通大学3号风洞中进行. 风洞试验段截面尺寸22.5 m × 4.5 m，风速范围1.0～16.5 m/s.试验段底壁设有转盘，可实现风向角的变换. 试验采用5 kg、5分量天平测量悬挑底部的基底力，并用激光位移传感器测量悬挑尖端的位移响应.

综合考虑结构尺寸、地形特点，及阻塞率要求，在风洞中最大限度地还原了桥址处地形. 模型几何缩尺比为1∶50. 模型主梁长1.4 m，最宽位置0.463 m，在风洞中的阻塞率小于5%，满足试验要求.

1.2 大气边界层模拟

试验段配备由尖塔、挡板和粗糙元等组成的边界层模拟装置. 试验设计了3种风场，并在2种风速下分别进行. 经测量，3种风场特性参数如表1所示.表中： Um为试验风速； Uf为实际风速； Iu、 Iw分别为 u 、w方向紊流度； Lu、 Lw分别为 u 和 w 方向紊流积分尺度. 模拟风谱在桥梁抖振所依赖的折算频率范围内（ f ＞10-1）与von Kármán谱吻合良好，满足抖振试验要求.

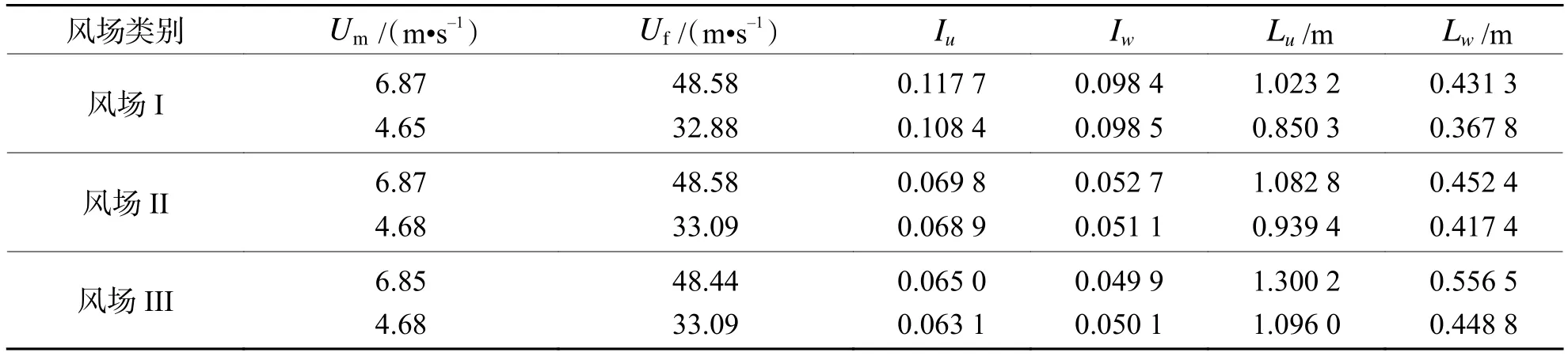
表1 各类风场特性参数Tab.1 Characteristic parameters of wind fields

1.3 试验工况

试验共分两部分，第1部分为刚性模型测力试验，获得结构静力三分力系数；第2部分为通过拟弹性模型准确模拟结构动力特性，测量结构的抖振响应. 图1为模型风洞试验图. 由图1可知，廊桥周边山体均为近似垂直于水平面的悬崖. 当结构处于0°风向角时，来流向廊桥受风面几乎没有山体遮挡；当结构处于180° 风向角时，顺风向廊桥的受风面有部分山体遮挡，遮挡宽度约为桥长的1/4～1/3.

试验风攻角及风向角示意图如图2所示，图中：风攻角包含 - 3°、0°、 + 3°；三分力系数试验包括0°～180° 范围内风向角；抖振试验包括全部角度；试验在前述3种风场及2种风速下进行.

图1 模型风洞试验示意Fig.1 Schematic of model and wind tunnel test

图2 风洞试验风向角及风攻角示意Fig.2 Diagram of wind direction and angle of attack

2 静力三分力系数结果及分析

静力三分力系数是表征各类结构断面在平均风作用下受力大小的无量纲系数，反映了风对结构的定常气动力作用. 根据试验得到结构在体轴系下的静力三分力系数，如图3所示. 图中： CV、 CH、CM分别为升力系数、阻力系数和扭矩系数； α 为风向角.

由图3可知，随着风攻角和风向角变化，场地模型对风场影响明显，三分力系数变化较大. 3个风攻角各曲线随风向角改变的变化趋势大体相同，但系数值有明显差别. 因地形不对称等差异，0°～90° 和 90°～180° 的三分力系数未呈现对称的结果，前者各系数值普遍高于后者.

由于山体地形的影响，从0°～180° 随风向角改变 CV呈现明显的先增大后减小的整体趋势. 在来流风方向当山体处于桥体下风侧时，山体对来流风的阻挡引起风沿崖壁折向桥体的回流会使结构的CV增大，但因考虑当风向与崖壁垂直时悬崖对风能量的消耗也最大，因此， CV最大值未出现在90°.

CH呈现出先增大后减小、再增加后减小的趋势，其最大值出现在25° 附近. 随着风向角继续增大，风向与结构阻力方向（横桥向）夹角逐渐减小，至 90° 达到最小， CH达 到最小值. 而后 CH向相反方向增大至155° 附近达到最大，因山体在来流向的遮挡导致结构处平均风速降低， CH减小.

CM大体呈现先减小后增大再减小的趋势，0°和 + 3°风攻角 CM最大值出现在 10° 附近， - 3°风攻角 CM最大值出现在 135°. + 3° 和 0° 攻角在 90° 附近 CM减小到 0，而 - 3° 攻角在 45° 附近 CM已减小至0，且方向改变， + 3° 攻角下的扭矩系数方向基本没有变化.

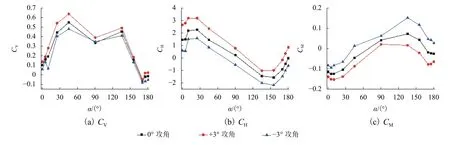
图3 三分力系数曲线Fig.3 Curves of aerostatic force coefficients

3 抖振响应结果及分析

3.1 抖振响应试验结果

根据《公路桥梁抗风设计规范》[9]（以下简称《桥规》）对限幅振动计算的规定，将此类廊桥结构视为桥梁的单悬臂状态，依据相关力学知识可知此类结构最大位移响应将发生在悬挑最外缘，试验选取该点进行测量.

经对各工况试验数据处理分析，得到模型在紊流场中的风致响应. 在3种风场、2种风速、3个攻角下，实桥横向、竖向及扭转3个方向的位移响应均方根（σx、σy、σθ）随风向角变化的曲线如图 4所示.

图4 各风场抖振响应变化曲线Fig.4 Structural buffeting responses in different wind fields

3.2 抖振响应结果分析

3.2.1 抖振响应随风向角的变化趋势

由图4可以看出，当结构位于山体上风侧（0°～180°）时，σx、σy、σθ均呈现明显的先减小后增大趋势，当山体处于结构侧面（0°附近）或部分山体位于结构上风侧（180° 附近）时，山体会引起来流风紊流度增大，致使结构响应均方根较大，因此结构处于 45°～135° 风向角内时其响应均方根较小，90°附近达到最小，其余风向角下结构响应均方根较大，且在180° 附近达到最大.

对于桥梁结构，其不仅受法向来流风影响很大，在具有一定风向角的斜风作用下结构具有同样大的不利影响[10-11]. 再考虑到结构所处当地风环境，国内外诸多学者已做了相当的实验，发现结构最不利响应值通常出现在与结构法向具有一定角度的斜风作用下，在悬挑屋盖中也观察到类似的现象[12]. 因此需对此类地处复杂山区的悬挑结构在斜风作用下的风致响应引起足够的重视.

当结构位于山体下风侧（180°～360°），在来流向随着山体对结构遮挡面积的增大，结构尖端各响应均整体呈现减小的走势，但在来流向山体刚好遮挡在结构尖端附近时，引起结构尖端局部紊流度增大，致其抖振响应增大，即风向角在180°～360° 范围内抖振响应整体呈现先减小后增大的趋势，且在225° 及 300° 附近出现局部峰值. 观察结构在山体上风侧（60°～120°）和结构处在完全被山体遮挡的下风侧（240°～300°），引起前者结构响应的脉动风主要由来流风的脉动成分提供，后者在此基础上加之由山体及桥塔引起的脉动成分. 虽然后者结构被山体及桥塔遮挡，但其抖振响应并未呈现整体低于前者的态势，甚至部分响应高于前者. 因此抖振响应不仅要考虑桥塔风效应的影响[13]，山区风环境下结构位于山体下风侧时地形的干扰亦需加以重视.

3.2.2 风攻角对抖振响应的影响

在同一风速下，不同风攻角下的抖振响应变化趋势大体相同，同一风向角下各攻角抖振响应差值相对较小，仅在个别位置出现较大差异，且没有明显的规律，可以发现在此 ± 3° 较小幅度范围内，不同风攻角对结构抖振响应的结果影响不大.

3.2.3 风速对抖振响应的影响

通过2种不同风速下所得抖振响应值发现，风速对结构抖振响应随风向角改变的变化趋势几乎没有影响，但其对各响应值的影响较为显著，较高风速下各抖振响应值均明显大于低风速下的各项响应值. 比较发现，本次试验较高风速约为低风速的1.5倍，高风速下 σx约为低风速下 σx的1.5倍， σy约为低风速的1.8倍， σθ约为低风速的1.9倍. 风场II和风场III同样进行了2种风速的试验，结果与风场I相同，抖振响应图不再赘余.

3.2.4 紊流度对抖振响应的影响

在设计风速下，通过比较风场I和风场II结构抖振响应值探讨紊流度I的改变对结构抖振响应的影响，发现I的变化对不同方向抖振响应的影响不同. 当结构位于山体上风侧时，I的变化对 σx影响较小. 但随着I的增大 σy及σθ有较大变化，虽然其随着风向角的变化没有明显的规律性，但在各风向角下均明显增大. 由表1可知风场I较风场II的Iu增大约 40.7%，Iw增大约 46.4%. 在此定义 ∆σIi为随I的增大各抖振响应的增幅，由式（1）计算.

式中：i为 x、y、θ；σIi、σIIi分别为 I类和 II类风场横向、竖向、扭转抖振响应均方根； ∆σIi分别为由紊流度变化引起的横向、竖向、扭转抖振响应均方根的增幅.

在设计风速下3种抖振响应增幅随I增大的变化情况如图5所示，并将各工况下 ∆ σIi变化情况汇见表2.

3.2.5 紊流积分尺度对抖振响应的影响

紊流积分尺度是脉动风中紊流涡旋平均尺寸的量度，其大小决定了脉动风对结构作用的影响范围，如果紊流涡旋增大至可以将结构包含其中，则结构各部位所受的脉动风荷载会叠加，相反，脉动风荷载可能会互相抵消[14]. 通过比较在设计风速下的风场II和风场III中廊桥结构抖振响应值探讨积分尺度L的改变对结构抖振响应的影响. 由表1可知，风场III较风场II ，Lu增大约20.1%，Lw增大约23%. 在此，定义∆σLi为随L的增大各抖振响应的增幅，由式（2）计算.

式中： ∆ σLi为对应由积分尺度变化引起的各响应增幅； σIIIi为III类风场抖振响应均方根.

在设计风速下各抖振响应随L增大的变化情况如图6所示，并将结果汇总于表3.

由图6发现L变化对不同抖振响应影响不同.L的改变对 σx几乎无影响，各风向角 σy随L的增大整体呈现增大的趋势，各风向角 σθ在 ± 3° 攻角下随L的增大整体增大，但在0° 攻角下受L影响较小.

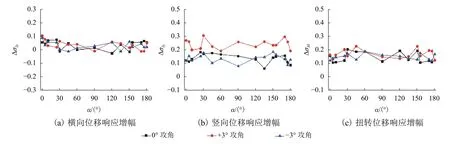
图5 各抖振响应随紊流度改变的增幅Fig.5 Increments of buffeting responses with the variation of turbulence intensity

表2 紊流度的变化对结构抖振响应的影响Tab.2 Effects of variation of turbulence intensity on the structural buffeting responses

图6 各抖振响应随紊流积分尺度改变的增幅Fig.6 Increments of buffeting responses with the variation of turbulence integral scale

表3 紊流积分尺度的变化对结构抖振响应的影响Tab.3 Effects of variation of turbulence integral scale on the structural buffeting responses

4 等效风荷载

自然风产生的风荷载由两部分组成：平均风作用产生的平均风荷载；脉动风引起的动力风荷载. 通常将后者分为脉动风的背景作用和结构惯性力作用. 现行各国桥梁抗风规范中计算一般只考虑顺风向风荷载，且对于顺风向风荷载的计算通常都忽略脉动风中与结构自振频率相近而产生的共振响应.《桥规》在桥梁静力风荷载作用计算时，可仅考虑静阵风荷载，且因抖振惯性力与平均风效应和背景脉动效应不能直接叠加，该规范静阵风荷载的计算方法亦为忽略抖振惯性力，在设计中将导致结果偏小，使设计偏于不安全. 该部分计算复杂且较难把握，为此将脉动风荷载等效为响应相同的静力风荷载成为十分有效的手段[3]. 鉴于此类人行桥梁结构与传统桥梁在外形及力的分配等方面存在明显的差异，其等效风荷载的获得有待研究，以便用于设计.根据实际地形情况，将桥址地形视为B类风场（抖振试验中风场I即为B类风场）进行计算分析.

对于桥梁结构来说，《桥规》中将平均风作用和风的背景脉动两部分合并，定义静阵风系数 GV为总响应与平均风响应之比，并给出了不同地表类别随水平加载长度变化的 GV的取值表格.

依据《桥规》可得结构在横桥向风荷载作用下主梁单位长度上的横向等效风荷载为[9]

式中： FH为作用在主梁单位长度上的静阵风荷载；ρ为空气密度； U0为静阵风风速；H为主梁投影高度.

根据随机振动理论，响应谱 Sx(ω) 、速度谱Sv(ω) 、 加速度谱 Sa(ω) 的关系为

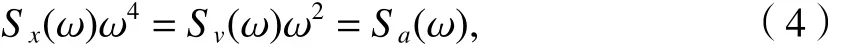
式中： ω 为圆频率.

本文抖振试验为结构在脉动风作用下产生的总的抖振响应. 因此可根据风洞试验抖振响应值，按照抖振惯性力计算公式[15]得到结构所受脉动风荷载，并与基于三分力系数结果得到的平均风荷载整合，获得结构静力等效风荷载.

结构每延米脉动风荷载为

式中： g 为峰值因子； l 为主梁长度； m (x) 为单位长度主梁质量； φ (x) 为 结构振型； σ (x) 为抖振位移响应均方根； x 为桥轴向坐标.

平均风荷载：

式中： U 为平均风速.

结构静力等效风荷载为

结构阻力系数及等效风荷载最大值出现在25°风向角，根据式（3）～（7）计算得到桥梁规范及基于风洞试验结构最大横桥向等效风荷载计算结果如表4，表中计算误差值为以风洞试验值为基础的《桥规》计算结果的误差值，即为二者差值与试验值的比值.

表4 等效风荷载计算结果Tab.4 Results of equivalent wind loading

文中观景廊桥属人行桥梁，但结构与传统桥梁结构有明显区别. 此结构固有频率高（结构一阶横向频率高达2.41 Hz）、刚度大，为特殊的单悬臂结构，且主梁包含箱梁及桁架梁两种结构形式. 通过桥梁规范以及风洞试验响应值对结构等效风荷载的计算比较发现，利用桥梁规范的计算结果明显高于试验值，规范设计偏于安全. 桥梁规范的计算忽略了脉动风谱中与结构自振频率相近的共振部分，通过静阵风系数将平均风作用和风的背景脉动放大得到二者的综合效应，即为静阵风荷载. 在将风的作用仅当作静力作用考虑并忽略共振部分原本是偏于不安全的，但因该结构水平加载长度小，频率高，共振部分影响小，按规范取值中静阵风系数过大，使静力风荷载作用放大较多，风荷载计算结果高于试验值30%，即使用桥梁规范计算该结构等效风荷载过于保守，对于此类结构桥梁规范的计算方法及静阵风系数取值有待商榷及进一步分析. 通过风洞试验获得的结构静力等效风荷载，综合考虑了平均风、脉动风的背景脉动，以及脉动风引起的共振部分，其每延米结构等效风荷载可直接用于结构设计.

5 结 论

（1） 随着风向角改变，结构三分力系数呈现规律的变化趋势，山体对三分力系数影响显著，其对来流风的阻挡导致平均风速的降低使阻力系数减小，且来流风沿崖壁向上的回流会使升力系数增大.

（2） 风向角在 0°～180° 和 180°～360° 内变化，抖振响应呈现明显先减小后增大的走势，结构在一定偏角的斜风作用下抖振响应达到最大，且当结构位于山体及桥塔下风侧时其抖振响应可能高于上风侧，结构设计时需加以重视.

（3） ± 3° 小幅度范围内风攻角对抖振响应的结果影响不大. 因同一风场风速不同引起标准差的变化，较高风速下各响应值明显大于低风速各响应值.

（4） 结构横向抖振响应受紊流度的变化影响较小，竖向及扭转响应随紊流度的增加增幅较大.

（5） 紊流积分尺度的变化对结构横向抖振响应几乎无影响，随着紊流积分尺度的增大，竖向响应相应增大，扭转响应在 ± 3° 攻角下整体增大，但在 0°攻角下受积分尺度影响较小.

（6） 针对此类频率高、刚度大的单悬臂结构，《公路桥梁抗风设计规范》对结构等效风荷载的计算偏于保守，静阵风系数取值有待修正. 基于试验获得的等效风荷载综合考虑了平均风及脉动风作用，可直接用于结构设计.