语言直觉模糊数的可能度排序方法及其应用
,,
(西华大学无线电管理技术研究中心, 四川 成都 610039)
美国控制论专家Zadeh在1965年提出模糊集[1],用隶属度来刻画事物的模糊性和不确定性并用[0,1]上的单个数值来表示。在1966年,学者Moorse提出区间值模糊集[2],即用一个[0,1]中的子区间表示隶属度,更进一步描述事物的模糊性,并在1979年提出区间值模糊集的基本运算及其应用[3]。随后,学者对区间值模糊集进行研究并对一组区间数进行排序,已有的排序方法可分为两类:一是确定性排序方法[2-5],二是基于度的排序方法[6-16]。确定性排序方法只能给出两个区间数的绝对大于、小于或等于关系,无法反映区间数所代表的不确定性,而基于度的排序方法既可以给出两个区间数的排序,又可以给出两个区间数之间相对大小的可能程度,还可以反映区间数的不确定程度;因此与确定性排序方法相比更具有适用性和理论研究价值。例如,徐泽水等[8]定义区间数的可能度并提出一种基于可能度的排序方法,以及在文献[8]中证明与文献[7]和[16]中提出的可能度公式等价。在1986年,又有学者Atanassov[17-18]将模糊集进行推广提出直觉模糊集,即用隶属度和非隶属度来描述事物的模糊性和不确定性,与模糊集相比在描述对象模糊性上更具有灵活性和适用性。随后学者将直觉模糊集转化到区间值模糊集上进行讨论。例如,Li[19]将直觉模糊数转化为区间数并定义直觉模糊数的可能度;Wei等[20]再次定义直觉模糊数的可能度并提出新的基于可能度的排序方法。
由于实际决策问题的复杂性和人类思维的模糊性,在含有不确定和不完备信息的决策问题中使用自然语言描述是直接有效的。为了应对语言描述固有的不确定性和含糊性,1975年,Zadeh提出语言变量[21]一词并建立模糊语言方法。2004年,Xu[22]提出不确定性语言变量和可能度定义以及不确定性语言加权聚合算子和不确定性语言混合聚合算子。考虑到直觉模糊集和模糊语言方法所具有的优势,在2015年,Chen等[23]提出语言直觉模糊数,用语言值表示隶属度和非隶属度,更进一步描述事物的模糊性和不确定性。他们同时提出一系列聚合算子,如有序加权平均聚合算子,并提出语言直觉模糊数的得分函数和精确函数对语言直觉模糊数进行排序。目前,在现有文献中关于语言直觉模糊数的排序方法和决策方法研究得比较少,并且对某些语言直觉模糊数的比较不合理,更重要的是语言直觉模糊数在处理决策问题中更具有优势,值得进一步研究。
1 预备知识
1.1 直觉模糊集
定义1[17]设X是一个非空论域,定义在X上的直觉模糊集表示为A={

定义2[18]设a1=
1)u1≥u2,v1
2)u1=u2,v1=v2时,则a1=a2;
3)u1>u2,v1>v2时,则a1,a2无法比较。
定义3[20]设a1=
(1)
上述可能度公式与文献[7,8,16,20]中提出的可能度公式等价,此处不做详细证明。
例1 设a=<0.5,0.3>,b=<0.4,0.2>,c=<0.2,0.5>都是直觉模糊数。

1.2 模糊语言方法
模糊语言方法是一种通过语言变量语义使用语言值表示定性方面的近似技术。
定义4[25]设S={s0,s1,s2,…,sg}是一个给定的有序语言项集,si表示语言变量的可能取值,g取自然数。例如一个含有5个语言项的集合S,如下:
S={s0=none,s1=low,s2=medium,
s3=high,s4=perfect}
对∀si,sj∈S,其中i,j∈{0,1,2,…,g},满足以下性质:
1)有序性:如果i≤j,则si≤sj;
2)可逆性:neg(si)=sg-i;
3)取大算子:如果si≤sj,则sj=max(si,sj);
4)取小算子:如果si≤sj,则si=min(si,sj)。

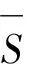
1)sα⊕sβ=sβ⊕sα=sα+β;
2)sα⊗sβ=sβ⊗sα=sαβ;
3)λsα=sλα;
4)(sα)λ=sαλ。
由文献[28]知道,语言项的计算可直观地看成语言项下标计算。
1.3 语言直觉模糊集
直觉模糊数是采用[0,1]上的实数来表示隶属度和非隶属度的。然而,在大多数情况下,由于环境的复杂性和人类思维的含糊性,决策信息是不确定的、模糊的,精确地数字不再适用于这些决策问题;因此,引入用语言值表示隶属度和非隶属度的语言直觉模糊数。
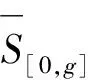
定义7[23]设∀
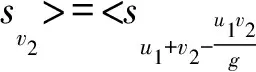

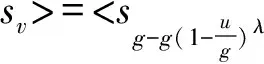

与直觉模糊数类似,Chen等[23]提出语言直觉模糊数的语言得分函数和语言精确函数并给出任意两个语言直觉模糊数的比较方法。
定义8[23]设γ=(su,sv)∈Γ[0,g],记Ls(γ)=u-v,Lh(γ)=u+v,称Ls(γ)、Lh(γ)为γ的语言得分函数和语言精确函数。
定义9[23]设∀γ1=(su1,sv1),γ2=(su2,sv2)∈Γ[0,g],有以下关系:
1)如果Ls(γ1)>Ls(γ2),那么γ1>γ2;
2)如果Ls(γ1) 3)如果Ls(γ1)=Ls(γ2), (ⅰ)若Lh(γ1)>Lh(γ2),则γ1>γ2; (ⅱ)若Lh(γ1) (ⅲ)若Lh(γ1)=Lh(γ2),则γ1=γ2。 显然,对∀(su,sv)∈Γ[0,g],有(s0,sg)≤(su,sv)≤(sg,s0)。 定理1[23]设γ1= 为了将决策信息聚集,本文引入一个常用的聚合算子,如下。 (2) 定义11 设∀α1= (3) 为α1大于α2的可能度。 定义12 设∀α1= (4) 为α1大于α2的可能度。 定理2 设∀α1= 1)1≥p(α1>α2)≥0; 3)互补性:p(α1>α2)+p(α2>α1)=1; 证明显然,根据定义,以上性质成立。 对于语言直觉模糊数,Chen等[23]定义语言得分函数和语言精确函数并提出基于语言得分函数和语言精确函数的比较方法。此处结合语言直觉模糊数的可能度,得到如下结论。 必要性。设Ls(α1)≥Ls(α2),即u1-v1≥u2-v2⟺u1+v2≥u2+v1。 当u1≤u2,v1>v2oru1 当u1 综上所述,故定理3得证。 根据上述分析,结合可能度和语言精确函数定义任意两个语言直觉模糊数的序关系。 定义13 设∀α1= 当Lh(α1)=Lh(α2)时,则α1≈α2。 对于一系列语言直觉模糊数,把它们进行两两比较,根据定义12计算出可能度并构造出一个可能度矩阵P=(p(α1>α2))n×n,该矩阵包含所有语言直觉模糊数两两比较的全部信息。于是可以得到以下结论。 定理4 可能度矩阵P=[p(α1>α2)]n×n是一个模糊互补判断矩阵。 证明由定理2的性质1)、3)即可证明。 根据文献[24],将可能度排序问题转化为求解可能度矩阵的排序向量即优先权重问题,其排序向量由如下公式计算: (5) 基于优先权重越大其值越大的思想,于是结合语言精确函数给出任意两个语言直觉模糊数之间的比较方法。 定义14 设∀α1= 2)如果w1=w2,那么 当Lh(α1)=Lh(α2)时,则α1≈α2。 根据以上所述,本文设计出一个关于语言直觉模糊数的可能度排序方法,如下: Step1:根据定义12中的公式(4)计算任意两个语言直觉模糊数之间的可能度p(ai>aj)(i,j=1,2,…,n)并构造可能度矩阵P=(p(ai>aj))n×n; Step2:再根据公式(5)计算出每一个语言直觉模糊数αi的优先权重wi; Step3:然后计算每一个语言直觉模糊数αi的语言精确函数Lh(αi); Step4:最后依据定义14,得到一系列语言直觉模糊数的排序结果。 例2 设4个语言直觉模糊数γ1= Step1:根据定义12中的公式(4)计算γi(i=1,2,3,4)偏好度并构造偏好度矩阵为 Step2:再根据公式(5)计算每一个语言直觉模糊数γi对应的优先权重,得到其排序向量为w=(0.2584,0.375,0.125,0.2416)。 Step3:计算每一个语言直觉模糊数γi对应的语言精确函数,得Lh(γ1)=7.531和Lh(γ2)=7.402,Lh(γ3)=7.086,Lh(γ4)=7.292。 在多属性决策中,属性权重是一个重要的研究课题。在实际的应用中,由于专家具有不同的知识领域和不同的偏好等因素,因此属性权重对于不同的专家具有不同的重要性。可以说,对于不同的专家,属性权重相同是一种特殊情况。例如,新城的建立需考虑地理环境、人口、经济、文化等因素,有的专家认为地理环境先天影响着城市今后的建设发展,有的专家则认为经济是影响城市建设的重要因素。因此,不同的专家应该具有不同的属性权重是合理的。于是设 基于上述分析,一个语言直觉模糊环境下基于可能度的多属性群决策方法概括如下: (6) (7) 其中,υ=(υ1,υ2,…,υl)Τ是专家权重。 Step3:根据公式(4)计算方案ai与ai*对应的整体综合值ri与ri*的偏好度为pii*,并构造构造可能度矩阵P=(pii*)m×m(i,i*=1,2,…,m); Step4:根据公式(5)计算出ri(i=1,2,…,m)对应的优先权重wi及其排序向量; Step5:然后由定义8计算ri(i=1,2,…,m)对应的语言精确函数Lh(ri); Step6:最后根据定义14,得到所有ri(i=1,2,…,m)的排序结果以及选择最佳方案。 引入文献[23]中的例子,一个语言直觉模糊信息环境下寻求全球最佳供应商的多属性群决策问题。 设A={a1,a2,a3,a4}是一个含有4个潜在全球供应商的集合即备选方案集,评价准则即属性集C={c1,c2,c3,c4,c5},其中cj(j=1,…,5)分别表示生产成本、产品质量、服务水平、供应商的利益以及风险因素。4个决策者给定的有序语言项集 S={s0=extremly poor,s1=very poor,s2=poor,s3=slightly poor,s4=fair,s5=slightly good,s6=good,s7=very good,s8=extremely good}。 接下来利用本文所提出的决策方法选择最佳方案。 Step1:假设专家dk(k=1,2,3,4)的属性权重分别为 ω1=(0.14,0.17,0.26,0.13,0.30)T, ω2=(0.17,0.27,0.16,0.20,0.20)Τ, ω3=(0.17,0.15,0.30,0.20,0.18)Τ, ω4=(0.17,0.32,0.18,0.20,0.13)Τ。 r1=(s5.388,s2.108),r2=(s6.111,s1.306), r3=(s5.180,s1.986),r4=(s5.352,s1.914)。 Step3:根据公式(4)计算方案ai与ai*即ri与ri*的偏好度pii*,并构造构造可能度矩阵为P=(pii*)m×m(i,i*=1,2,3,4): Step4:根据公式(5)计算出方案ai即ri(i=1,2,3,4)的优先权重及排序向量为 w=(0.206,0.375,0.164,0.255)。 Step5:由定义8计算ri(i=1,2,3,4)的语言精确函数Lh(ri)为 Lh(r1)=7.496,Lh(r2)=7.417, Lh(r3)=7.166,Lh(r4)=7.266。 Step6:最后根据定义14的序关系,得到ri(i=1,2,3,4)的排序结果为r2>r4>r1>r3,即是方案a2最优,方案a4次之,方案a1再次之,而方案a3最差。 由定义8计算ri(i=1,2,3,4)的语言得分函数Lh(ri)为Ls(r1)=3.280,Ls(r2)=4.805, Ls(r3)=3.194,Ls(r4)=3.438,显然有Ls(r2)>Ls(r4)>Ls(r1)>Ls(r3),再根据文献[25]中提出的比较方法可得它们排序结果为r2>r4>r1>r3即a2>a4>a1>a3,同本文的排序结果相比,其排序相同。因此,本文提出的语言直觉模糊环境下基于可能度的排序方法是合理有效的。特别地,考虑两个语言直觉模糊数γ1= 本文受到区间可能度和不确定语言变量的可能度定义的启发,针对语言直觉模糊数的比较排序,结合Atanassov偏序对可能度的定义范围进行适当改进提出语言直觉模糊数的可能度定义,并且讨论一些相关性质。通过构造可能度矩阵将比较排序问题转化为求解排序向量即优先权重的问题,并提出基于可能度的语言直觉模糊数排序方法。该方法不仅具有Atanassov偏序的确定性排序优点而且还具有基于度的排序优点,既可以给出两个语言直觉模糊数的大小比较,又可以给出两者相对大小的可能程度,更具有实用价值和理论研究价值。这种方法和基于得分函数和精确函数的粗糙的确定性排序方法比较起来,其计算结果更加精确更具有说服力。本文提出的可能度排序方法可推广到其他方面,如犹豫模糊集。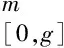

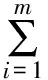
2 语言直觉模糊数的可能度排序方法
2.1 语言直觉模糊数的可能度
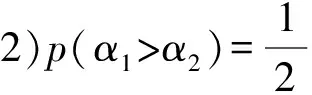
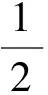


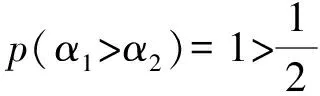



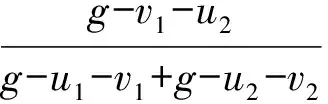


2.2 语言直觉模糊数的可能度排序方法




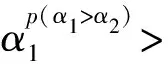
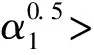

3 语言直觉模糊环境下基于可能度的多属性群决策方法
3.1 语言直觉模糊环境下的多属性群决策问题

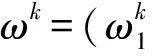
3.2 语言直觉模糊环境下基于可能度的多属性群决策方法
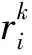


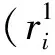
4 案例分析
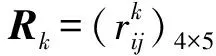
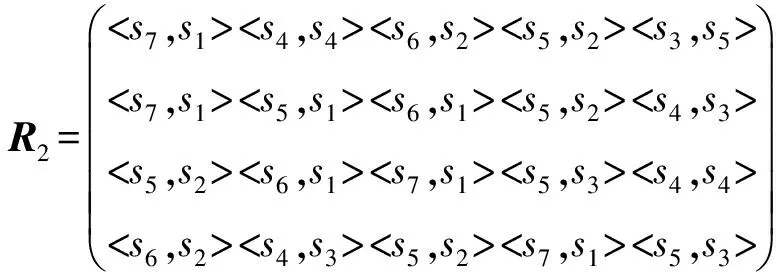
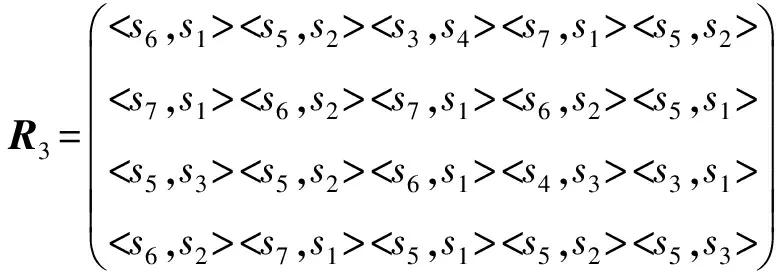
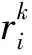

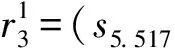




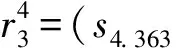
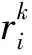

5 结论

