基于分段快速模拟退火的零偏VSP全波形反演

韩璇颖,印兴耀,曹丹平,梁 锴

(1.中国石油化工股份有限公司石油物探技术研究院,江苏南京211103;2.中国石油大学(华东)地球科学与技术学院,山东青岛266580)

VSP技术作为一种井中地震勘探方法,在地面地震、钻井和地质资料间发挥了桥梁作用。利用VSP资料可获得井口附近地震频带尺度的可靠参数,利用该参数可进行地震地质层位的标定,成果解释及油气预测[1-2]。

STEWART[3]和LINES等[4]系统地研究了利用旅行时反演VSP资料速度的方法;邹强等[5]利用阻抗和旅行时联合反演层速度;姚忠瑞等[6]以北101井VSP测井为例,利用零偏VSP资料求取横波速度;受旅行时拾取的误差和地震波能量等多种因素的影响,得到的横波速度不准确[7]。全波形反演充分利用了旅行时及波场相关信息(如振幅、频率和相位等)提高了反演的精度[8-9]。OWUSU等[10]利用阿拉伯湾VSP资料进行全波形反演建立了合理的速度模型;EGOROV等[11]基于全波形反演得到了VSP资料的纵波速度及其数值范围。

采用模拟退火(simulated annealing,SA)算法进行零偏VSP全波形反演可以克服传统局部优化算法过于依赖初始模型和易陷入局部极值的不足[12-15]。作为一种非线性优化算法,在足够的模型扰动和迭代次数以及严格退火方案的条件下,SA算法是有效的[16],但在实际应用中,因难以满足上述条件而导致该算法效率不高。尽管零偏VSP资料的数据量小,但将SA算法应用于耗时长﹑计算量大的零偏VSP全波形反演,效率问题不容忽视。

许多学者对SA算法加以改进以提高效率,INGBER[17]提出了一种VFSA算法;刘海飞等[18]将局部搜索能力较强的单纯形法和鲍威尔法引入SA算法,形成了基于SA算法的全局混合反演方法。李亚楠等[19]提出了一种改进的自适应差分演化算法,该算法融入了SA思想,提高了全局搜索能力。虽然这些改进在一定程度上解决了SA算法耗时长的问题,但将SA算法应用于零偏VSP全波形反演,计算效率仍然较低。改进的算法虽然提高了局部搜索能力但一定程度上限制了整个算法的全局搜索能力,不易得到精确解。

本文在VFSA算法理论框架下,将高效、高精度的SFSA反演策略应用于零偏VSP全波形反演,在不同阶段采用了不同的扰动模型和退火方式,反演前期采用大扰动空间和较慢温度衰减速度,充分发挥全局搜索能力,而后期采用小扰动空间和较快温度衰减速度,有效提高了局部搜索能力及收敛速度,最终在井孔周围获得了可靠的地层速度,为精确的时深转换及油气预测奠定了基础。

1 零偏VSP全波形反演的理论基础

全波形反演的基础为时间域声波波动方程有限差分正演。当震源为零时,二维各向同性均匀介质的声波方程为:

(1)

式中:v为纵波速度;f为波场;t为波传播的时间。我们采用空间四阶时间二阶交错网格差分方法[20]进行正演模拟。相较于地面地震资料,零偏VSP资料的数据量小,有利于全局优化算法的应用。

地震全波形反演的目标函数,可用于衡量真实数据和模拟数据之间的匹配程度。将L2范数作为目标函数,其形式为:

(2)

式中:F为目标函数;d为真实的零偏VSP资料;f(v)为当前速度模型的正演数据。在提高算法的效率同时为了避免陷入局部极值,本文将SFSA反演策略应用于零偏VSP全波形反演,在反演的前、后阶段分别采用相匹配的退火计划和扰动模型,前期侧重保留算法的全局优化性能,后期强化算法的局部搜索性能,总体上提高了反演的寻优效率及精度。

2 SA算法原理

2.1 退火计划

SA算法采用不断降低温度的手段来控制整个算法的进程。算法通常包括两种形式:快速衰减的温度和长马尔可夫链以及缓慢衰减的温度和短马尔可夫链。我们需要综合考虑计算效率和结果精度来平衡温度的衰减速度和马尔可夫链长度。温度衰减过慢,会使算法的效率变低,反之,则可能陷入局部极值[21]。通常我们选取的温度衰减速度较小,这是为了减小所需马尔可夫链的长度。本文采用的退火计划为[22]:

(3)

式中:T为当前温度;k为迭代次数;T0为初始温度;M为反演的参数数量(本文中M=1);α为接近1.0的常数,表示衰减的快慢,通常为0.7≤α<1.0。

2.2 引入限制因子的扰动模型的产生

SA算法的新模型基于当前模型扰动得出。蒋龙聪等[23]基于非均匀变异的思想提出了新模型参数公式为:

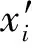
为进一步提高局部搜索能力和效率,本文在扰动模型中引入了一个限制因子,该因子与迭代次数k成反比,目的是在迭代不断增加的时候逐渐减小模型的扰动空间,即随着迭代次数的增加,扰动模型将在和当前模型不断逼近的范围中产生,从而更快得到最优解。新公式可以表示为:

(6)

式中:b为限制因子,b(k)=1/(mk),其中系数m控制模型扰动空间的变化。

2.3 VFSA算法理论框架下的SFSA反演策略

基于VFSA算法理论框架,在不同阶段分别采用不同的扰动模型和退火方式,相较于常规VFSA算法,本文提出了一种更具灵活性﹑高效和高精度的SFSA反演策略。根据该策略,可根据实际需要将反演划分成不同的阶段,分别调节不同阶段时模型扰动空间大小和温度衰减的速度。基本原则为在充分发挥全局优化性能寻找最优解范围的同时,快速收敛到最优解。本文将反演阶段划分为两段,迭代前期采用大扰动空间和较慢的温度衰减速度;迭代后期采用小扰动空间和较快的温度衰减速度。这里引入一个参数:截断迭代数K,以确定两段法的前、后期次。在前期,当迭代次数小于截断迭代数K时,扰动模型使用全局扰动模式,遍历整个解空间,采用传统的VFSA算法,可得:

(7)

与此时扰动模式相匹配的退火计划为α=0.99的公式(3),α值较大,温度衰减缓慢,可有效地搜索和锁定最优解的范围。在反演后期,即迭代次数大于截断迭代数K时,需快速收敛到最优解,为提高后期局部搜索的能力,我们使用公式(6)生成扰动模型,随着迭代次数的增加,扰动空间不断变小,不断逼近最优值,相应的退火计划为α=0.97的公式(3),α值较小,温度的衰减速度快。根据不同阶段的目的和特点,采用不同的公式,可提高整个反演过程的效率和精度。

3 测试及应用

3.1 系数测试

本文正演模拟的纵波速度模型如图1a所示,最大深度为900m;空间采样间隔Δx=Δz=10m;时间采样间隔为1ms;爆炸震源位于0处,产生主频为30Hz的雷克子波。在偏移距为20m处设置井位进行观察。图1b为正演得到的零偏VSP资料的地震记录。

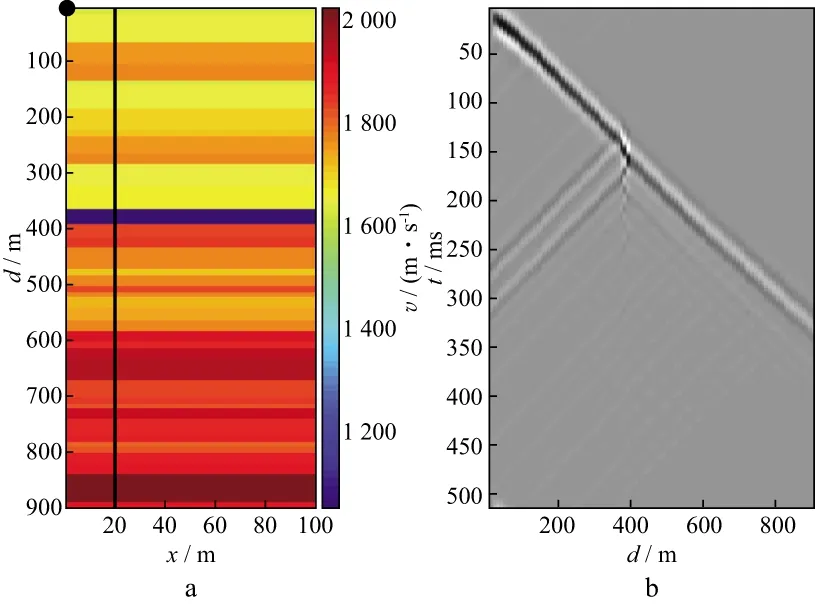
图1 纵波速度模型(a)和零偏VSP地震记录(b)

根据SFSA零偏VSP全波形反演的效果进行系数测试以确定m和K的最佳值。系数测试的初始温度为10℃,终止温度为1×10-6℃,马尔科夫链长为15,迭代次数为529。首先设定m值,取K=10,50,100,150,200,300时分别进行测试,反演效果最好的为该条件下的最佳K值;然后设定K值,取m=1,2,3,4,10,50时分别进行测试,反演效果最好的为该条件下的最佳m值。需要注意的是,当m<1时,迭代次数k略大于截断迭代数K,反演后期开始时,模型的扰动空间陡增(图2a),会使得前期得到的较小最优解空间没有意义,不符合随着迭代次数增加模型的空间扰动量不断减小的趋势。当m=0.5时,反演得到的速度与模型速度的对比如图2b所示,误差较大(图2c),反演效果不理想,因此m的值不应小于1。

当m=3的时候,速度反演结果如图3所示,可以看出,当K值较小(图3a)时,反演结果不理想;当K=100(图3b)时,反演的速度和模型速度对比误差最小,反演结果可靠;当K值较大(图3c)时,结果同样不理想。从温度和扰动空间随迭代次数的变化情况(图4)可以看出,K值较小时(图4a),温度降低快,尚未得到最佳扰动模型空间时,空间扰动量已经变小,算法易陷入局部极值;当K=100时(图4b),前期温度降低慢,空间扰动量较大利于充分寻优,后期温度快速降低,空间扰动量无突变的减小,变化较为合理;当K值较大时(图4c),反演后期空间扰动量陡降,会使扰动模型出现突变,不利于找到速度的最优解。

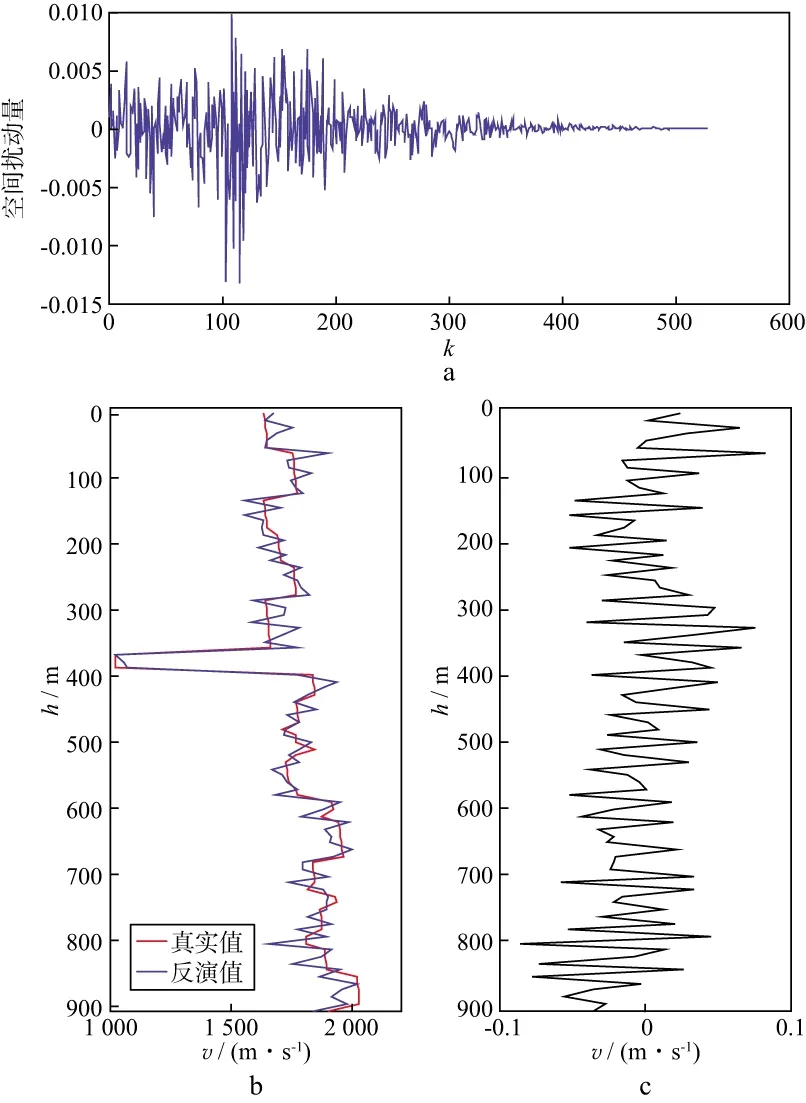
图2 m=0.5时的反演结果a 空间扰动量随迭代次数的变化情况; b 反演得到的速度与模型速度的对比; c 速度反演的误差

结合m=3且K=50,150,200的其他3组测试结果表明,K为[100,150]时,反演结果可靠。根据m=1,2,4,10,50时的测试结果可知,K取值[100,150]最合理。由于不同m对应最佳K的取值范围相同,故仅需对该范围内任意K值(如K=100)时m=1,2,3,4,10,50分别进行反演测试。K=100时,反演结果和模型的平均相对误差依次为2.35%,0.60%,0.53%,0.51%,3.64%,10.05%。图5 显示了K=100时部分m值的反演结果和误差曲线,可以看出,m太小或者太大均会导致不合适的扰动空间变化,影响反演的效果,m为[2,4]时,反演效果较理想。下文均采用K=100,m=3进行反演。

3.2 零偏VSP纵波速度反演

分别采用VFSA和SFSA反演零偏VSP资料的纵波速度。为验证SFSA反演的高效性和高精度性,我们进行了两组测试:反演Ⅰ和反演Ⅱ。初始速度均为1500m/s,终止温度均为1×10-6℃。

图3 不同K值对应的反演结果与真实值对比(m=3)a K=10; b K=100; c K=300

图4 温度和空间扰动量随迭代次数的变化情况a K=10; b K=100; c K=300

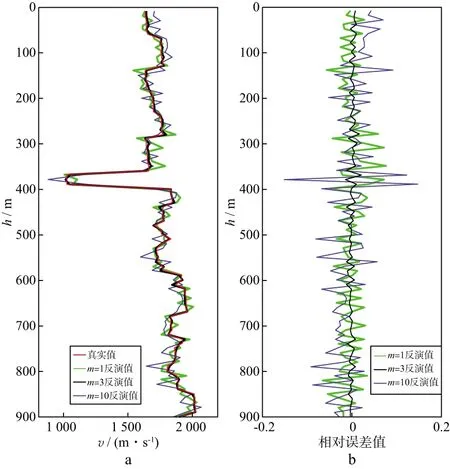
图5 不同m值对应的反演结果及误差曲线(K=100)a 反演的速度与真实速度的对比; b 速度反演的误差

反演Ⅰ的初始温度为100℃,马尔可夫链长度为200,VFSA反演和SFSA反演的迭代次数分别为912和604。反演Ⅰ的结果及误差对比如图6所示。分别将图6中两种反演方法得到的地震记录与真实模型得到的地震记录(h=600m)进行对比,结果如图7所示,可以看出,在反演Ⅰ中,两种反演方法都得到了理想的效果,但SFSA法迭代次数少,用时少,且误差小,相较于VFSA,其效率提高了约50%。

反演Ⅱ的初始温度为10℃,马尔可夫链长度为20,VFSA反演和SFSA反演的迭代次数分别为798和529,SFSA反演效率约为VFSA反演效率的1.5倍。图8a和图8b分别为VFSA反演和SFSA反演得到的速度与模型速度的对比,图8c为两种方法误差的对比,图9为两种方法反演得到的速度对应的地震记录与模型地震记录的对比,可以看出VFSA反演得到的结果误差较大,而采用SFSA反演可得到可靠解。图10为反演Ⅱ中分别采用VFSA反演和SFSA反演时能量随迭代次数的变化情况。能量代表着误差,在较低的初始温度和较短的马尔可夫链长度的情况下,VFSA反演后期能量收敛的速度很慢,故误差较大;而SFSA反演收敛速度相对较快,故在更小的迭代次数条件下SFSA反演可获得更好的效果。基于与反演Ⅱ相同的条件进行添加噪声测试,当地震记录的信噪比RSN分别为4和2时,反演结果及其与模型值的误差分别如图11和图12所示,可以看出,SFSA反演比VFSA反演的效率和精度更高。

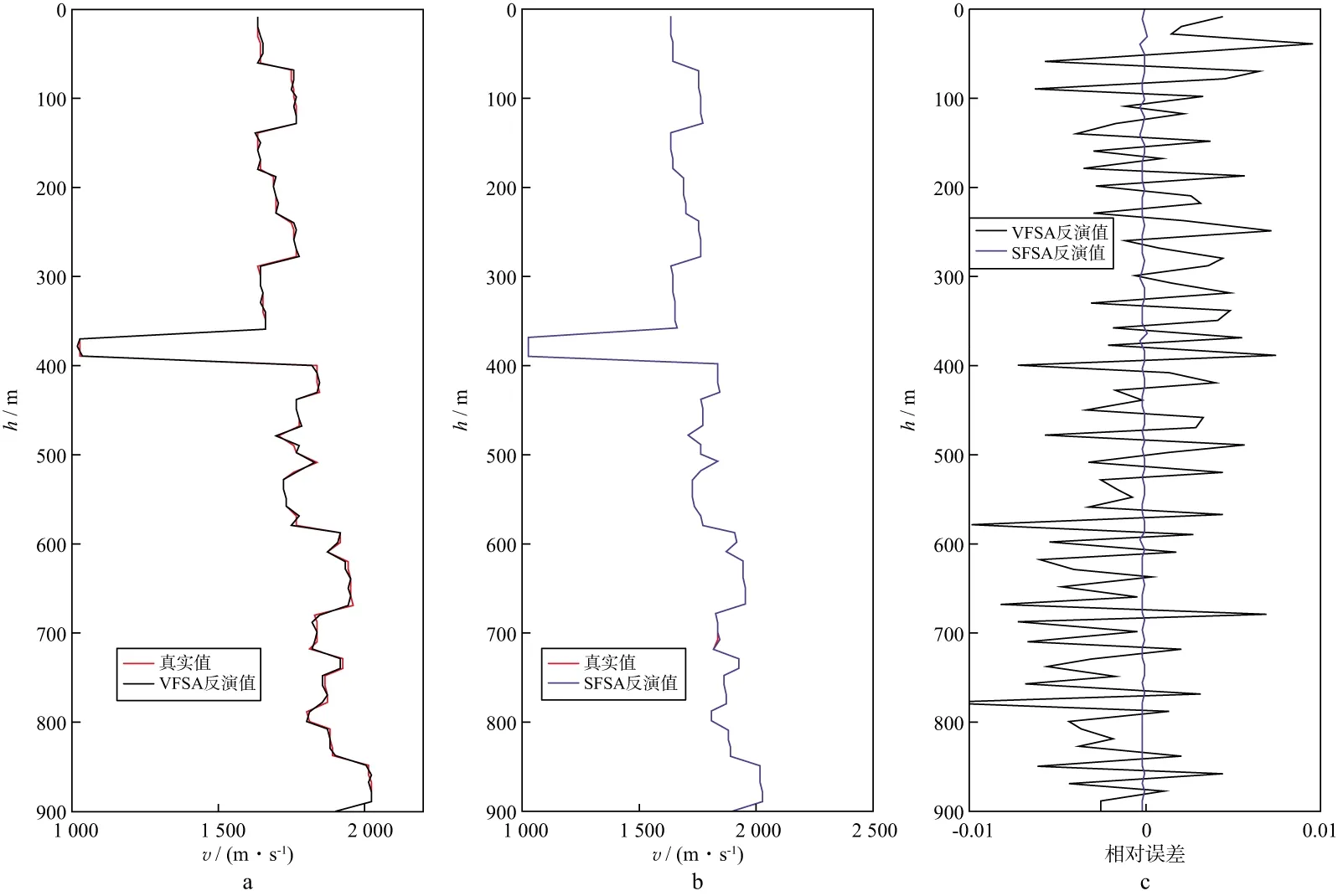
图6 反演Ⅰ的结果a VFSA反演得到的速度与真实速度; b SFSA反演得到的速度与真实速度; c 速度反演的误差

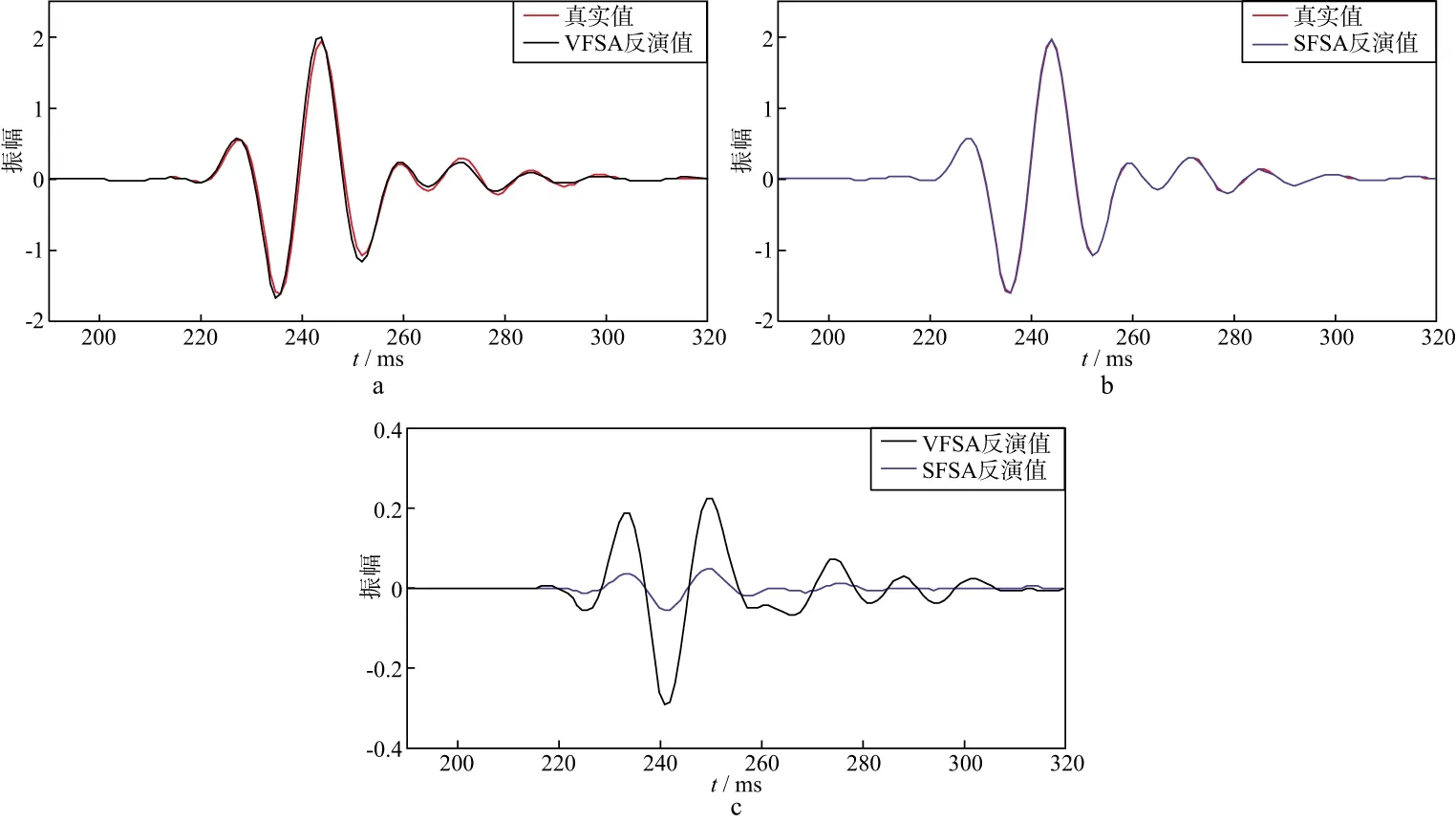
图7 反演Ⅰ得到的地震记录与真实模型得到的地震记录(h=600m)a VFSA; b SFSA; c 地震记录的误差

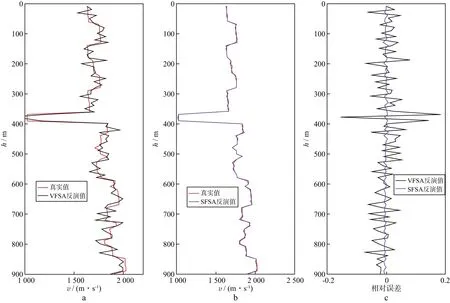
图8 反演Ⅱ的结果a VFSA反演得到的速度与真实速度; b SFSA反演得到的速度与真实速度; c 速度反演的误差

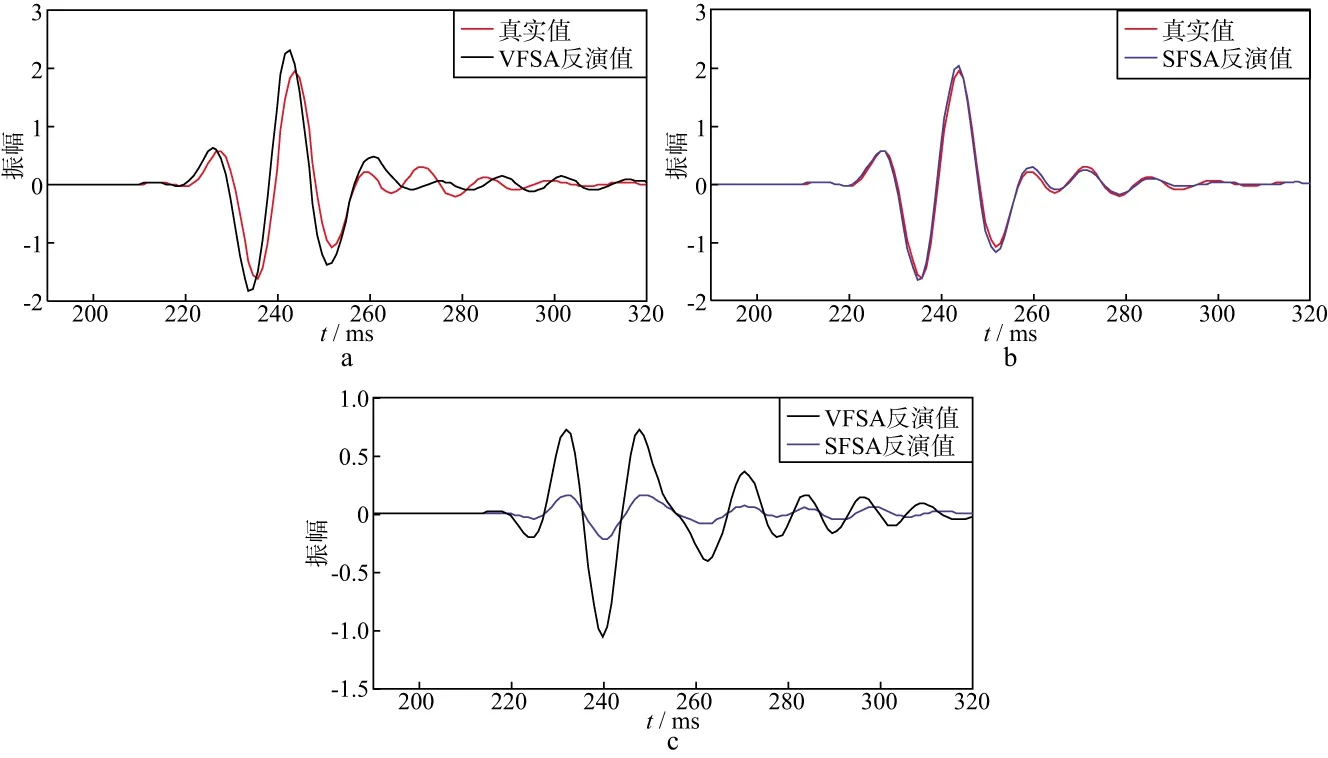
图9 利用反演Ⅱ的模型得到的地震记录与真实模型得到的地震记录(h=600m)a VFSA; b SFSA; c地震记录的误差

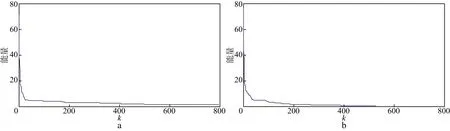
图10 反演Ⅱ中能量随迭代次数变化情况a VFSA; b SFSA

图11 添加噪声测试结果(RSN=4)a VFSA反演得到的速度与真实速度; b SFSA反演得到的速度与真实速度; c 速度反演的误差

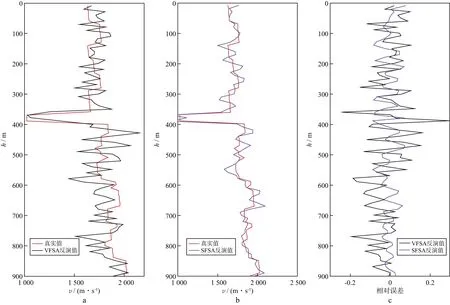
图12 添加噪声测试结果(RSN=2)a VFSA反演得到的速度与真实速度; b SFSA反演得到的速度与真实速度; c 速度反演的误差

4 结束语

本文提出将SFSA反演策略应用于零偏VSP全波形反演。以两段法为例,将反演分为前、后两个阶段,前期有效锁定最优解的范围,后期反演结果快速收敛。模型测试证明,SFSA反演可明显提高收敛速度,效率约为基于VFSA反演的1.5倍,还可以在比VFSA反演迭代次数更少的情况下获得更可靠的纵波速度。基于SFSA的零偏VSP全波形反演具有高效性和高精度性,这为之后地震地质层位标定,成果解释及油气预测奠定了基础。本文仅讨论了反演过程中m和K的取值范围,二者最优值的选取还需要进一步研究。