基于单道SVD和振幅比的地面微地震资料去噪方法
胡永泉,黄建波,田志华,潘树林
(1.成都工业学院计算机工程学院,四川成都611730;2.中国石油新疆油田分公司工程技术研究院,新疆克拉玛依834000;3.西南石油大学地球科学与技术学院,四川成都610500)
随着油气资源需求量的不断增加和常规油气资源的不断消耗,非常规油气资源的勘探与开发得到快速发展。其中,页岩气因其蕴藏量丰富、开采周期长等优势而备受青睐。页岩气勘探与开发技术的进步主要受到水力压裂技术发展的制约[1-3],而微地震作为一种监测水力压裂效果的关键技术,可通过对微地震有效信号的识别,利用定位与成像技术反演出水力压裂产生裂缝的方位和尺寸,进而为压裂效果评价与施工方案的调整提供指导性意见[4-7]。目前,微地震技术分为地面微地震和井中微地震两种。相对于井中微地震,地面微地震具有便于施工、观测点充分等优点,具有更广阔的发展前景。然而,地面微地震资料噪声种类多、能量强,资料信噪比极低,有效微地震信号完全淹没于噪声之中,采用常规去噪方法很难得到理想的效果,不利于有效信号的识别与震源定位[8-10]。因此,寻找合适的去噪方法是微地震资料处理与解释的关键[11-13]。
近年来,国内外专家学者针对地面微地震资料特点做了很多研究,并提出了适用于地面微地震资料的去噪方法,主要包括:经验模态分解互信息熵的去噪方法[14]、高精度字典学习算法的去噪方法[15]、τ-p域有效事件时差校正噪声压制法[16]、曲波变换自适应去噪法[17]、时频域S变换去噪法[18]、地面阵列式盲源分离去噪方法[19]、Shearlet变换去噪方法[20]、单道SVD去噪方法[21]、字典训练小波域稀疏表示去噪方法[22]、SVD与经验模态分解(empirical mode decomposition,EMD)联合去噪方法[23]等。这些微地震资料去噪方法大多只能较好地压制特定种类的噪声,将其直接用于四川某地区地面微地震资料的噪声压制处理,效果不尽理想。
鉴于此,本文提出一种基于单道SVD与振幅比的联合去噪方法。该方法首先采用振幅比法压制微地震资料中的随机噪声,然后采用单道SVD去噪方法压制单道微地震记录中的强周期性噪声,从而达到有效压制噪声,提高微地震资料信噪比的目的。将此联合去噪方法应用于实际微地震资料的处理,取得了较为理想的效果。
1 方法原理
1.1 SVD去噪
SVD去噪采用地震记录构建分解矩阵,然后将矩阵进行分解和变换,求取矩阵的奇异值(奇异值逆序排列),其中较大奇异值对应各道间相关性较强信号,较小奇异值对应随机干扰。在实际应用中,选取奇异值序列中前列几个数值较大的奇异值进行矩阵重构(低通滤波),突出各道之间相关性较强的信号;选取部分中间奇异值进行矩阵重构(带通滤波),突出具有一定相关性的信号;选取最后几个数值较小的奇异值进行矩阵重构(高通滤波),用于提取随机噪声[24-25]。
假设微地震资料剖面有M道,每道N个记录点,由此产生的矩阵用A表示,其中元素为aij(i代表道号,j代表记录点序号),即:
(1)
对矩阵A进行奇异值分解可表示为:
(2)
式中:U是由AAT的特征值向量构成的正交矩阵;V是由ATA的特征值向量构成的N×N的正交矩阵;Σ是由奇异值σx按从大到小顺序构成的一个对角矩阵。
(3)
式中:r为矩阵A的秩,矩阵奇异值满足σ1≥σ2≥…≥σr≥0。
(4)
在实际重构中,奇异值的选择取决于地震资料有效信号的相关性。通常情况下,有效信号相关性越强,重构所需要的奇异值越少。然而,地面微地震资料有效信号较弱,同相轴连续性较差,采用常规SVD方法无法达到提高信噪比的目的。鉴于此,针对单道微地震记录周期性干扰较强的特点,采用单道SVD去噪方法进行处理。
1.2 单道SVD去噪
本文的单道SVD去噪方法是在传统SVD去噪方法基础上针对微地震信号中噪声的强周期性提出的,其原理如图1所示。图1显示了单道微地震记录的部分数据,由于有效信号较弱,呈现的基本是噪声信号,可见,对于单道微地震记录而言,强周期性干扰较为严重。若对规律性较强的周期干扰进行有效压制,可较好地突出微地震资料的有效信号。
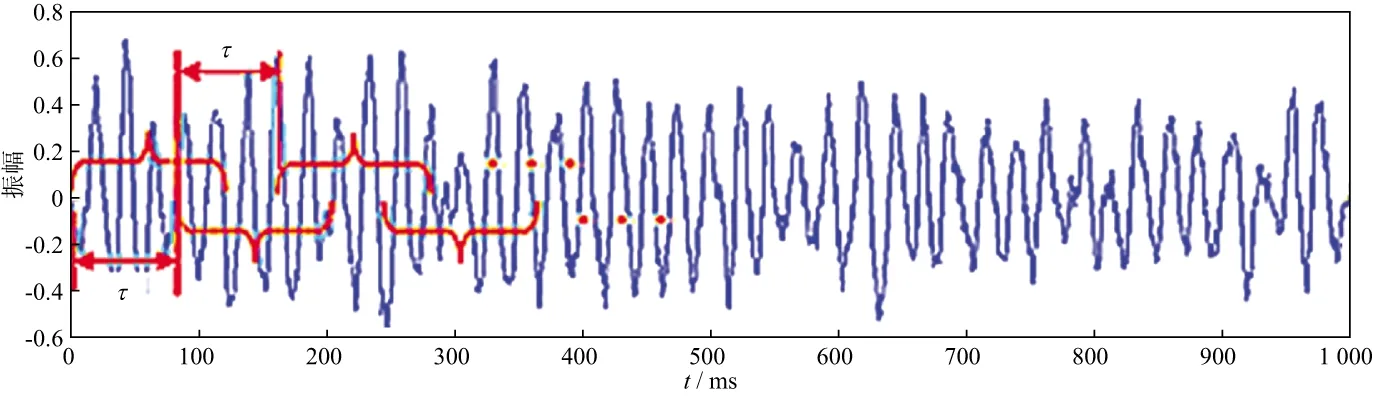
图1 单道SVD去噪原理
首先,单道SVD根据设定的时间延迟量τ将微地震记录分成相关性较强的若干段,并采用分段记录创建分解矩阵Am。随后对分解矩阵进行奇异值分解,并根据实际微地震资料强周期干扰的分布规律选取部分中间奇异值进行单道微地震记录的重构,从而达到压制周期干扰,突出有效信号的目的。
设单道微地震记录的采样点数为N,根据设定的时间延迟量τ将单道微地震记录分为m-1段,确保各段记录之间周期干扰信号相关性较强,由m-1段记录构成的分解矩阵Am表示为:
(5)
式中:m代表矩阵维数;τ代表时间延迟量;n代表每个分段的采样点数。各参数之间关系可表示为:
(6)
对矩阵Am进行分解,奇异值构成可表示为:
(7)
式中:SA是矩阵Am的全部奇异值;SW代表数值较大的部分奇异值,与单道微地震资料中的强周期干扰相对应;SD代表数值居中的奇异值,该部分奇异值是微地震资料重构的关键,包含绝大多数微地震有效信号;SN代表数值较小的奇异值,主要对应随机噪声。在矩阵重构时,保留SD,并将SW和SN充零,这样经过SVD反变换可有效地压制强周期干扰和随机噪声。依次对所有道进行计算,最终便可得到去噪后的微地震剖面。
单道SVD去噪方法的有效性主要取决于矩阵Am参数的取值。其中,时间延迟量τ是决定最终效果的关键。它不但决定了Am各分段记录的相关性,还间接限定了Am其它参数的取值。本文采用单道微地震记录自相关归一化方法求取τ值,从而改善固定取值不能适应每道记录特点的不足。τ值求取可表示为:
(8)
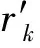
由于单道SVD去噪是选取数值大小居中的部分奇异值进行记录重构的,这就要确保矩阵分解后奇异值个数不能过少,否则,很难从中选取适合的奇异值进行重构。由于分解矩阵奇异值的个数与Am的秩相等,为了防止奇异值个数过少现象的产生,本文将由单道微地震记录分段构成的分解矩阵维数m和每维记录点数n设置为相同数值,将m=n代入(6)式变换可得:
(9)
1.3 振幅比法去噪
借鉴能量比法原理,振幅比法同样利用时窗内信号统计规律进行噪声压制。与能量比法不同的是,振幅比法采用一个固定时窗和一个扩展时窗来求取振幅比,其原理如图2所示。
首先计算参考点p处固定时窗和扩展时窗内信号的振幅和,即:
图2 振幅比法原理示意
式中:Eg(p)为参考点p处固定时窗内信号的振幅和;Es(p)为参考点p处扩展时窗内信号的振幅和;T0为单道微地震记录的起始时间;T1为参考点p处固定时窗的起始时间;T2为参考点p处固定时窗和扩展时窗的终止时间;x(t)为时窗内微地震记录采样点的振幅取值。两个时窗的振幅比为:
(12)
式中:R(p)代表参考点p处的振幅比。依次滑动两时窗,逐一计算所有点的振幅比,随后,找出最大振幅比,从而得到单道微地震记录各点的归一化振幅比,即:
R′(p)=R(p)/max{R(p)},p=1,2,…,N
(13)
式中:R′(p)为微地震记录各点归一化的振幅比;max{·}为最大值运算,即求取微地震记录各点的最大振幅比。最后,采用归一化的振幅比作为滤波因子对微地震资料进行去噪,即:
(14)
振幅比去噪方法采用扩展时窗代替固定时窗,当时窗内信号以随机噪声为主时,振幅和趋近于零,当存在有效信号时,振幅和绝对值较大,可以更好地突出有效信号。这在较大程度上削弱了随机噪声对振幅比法的影响,保证了有效信号得到更好的突出。对于振幅比法,固定时窗长度选择直接关系到方法效果的好坏,若长度过短,振幅叠加无法有效压制噪声;若长度过长,导致固定时窗与扩展时窗内信号振幅和相当,其振幅比无法突出有效信号。在实际资料处理中,固定时窗在80~200ms选择为宜,伸缩时窗长度至少为固定时窗的两倍。
1.4 单道SVD与振幅比联合去噪
由上述分析可知,单道SVD去噪方法可有效压制单道微地震记录中的强周期性干扰,然而对随机噪声的压制效果并不理想;振幅比法利用有效信号和噪声的统计特性差异,可有效压制微地震记录中的随机噪声,然而对强周期性干扰的压制并不理想。综合两种去噪方法的优点,本文采用单道SVD与振幅比联合去噪方法进行地面微地震资料去噪。
首先,采用振幅比法压制微地震剖面中的随机噪声。利用公式(13)计算两个时窗内振幅比R′(p),以此作为滤波因子对资料进行去噪。在实际应用中,为了削弱噪声统计规律对去噪效果的影响,振幅比法中固定时窗长度在80~200ms选取较为合适,兼顾去噪效果和计算效率,扩展时窗长度定为固定时窗的2倍。经过振幅比去噪后,剖面中的噪声主要为单道记录中的强周期干扰,这为单道SVD去噪方法的使用提供了良好的前提条件。
其次,采用单道SVD去噪方法进一步压制单道记录中的强周期干扰。单道SVD去噪效果的好坏主要取决于分解矩阵各道之间的相关性,为了确保各道之间具有较强的相关性,采用归一化自相关方法公式(8)确定时间延迟量τ,再由公式(9)计算分解矩阵维数和每维记录点数。由于单道SVD去噪的目的在于压制各道之间相关性较强的周期干扰,因此在矩阵重构时选取奇异值序列中间部分奇异值以达到压制强周期干扰和随机干扰的目的。在实际应用中,重构奇异值取值范围占奇异值序列的15%~45%为宜。
2 测试及应用
2.1 理论模型测试
2.1.1 单道SVD理论模型测试
图3为模拟微地震记录。由图3可见,在200ms,400~700ms存在两条有效信号同相轴。为验证单道SVD去噪方法的有效性,在单道记录中加入周期性较强的干扰信号。
图4是采用单道SVD方法去噪后的重构剖面,其中,时间延迟量τ采用自相关归一化方法求取。

图3 单道SVD理论模型微地震记录

图4 采用单道SVD方法的重构结果(采用自相关归一化法确定时间延迟量)a 各分解矩阵对应时间延迟量τ曲线; b 第一道模拟记录构建的分解矩阵对应的奇异值序列; c 奇异值序列比例<6%; d 奇异值序列比例为6%~45%; e 奇异值序列比例为10%~45%; f 奇异值序列比例为15%~45%; g 奇异值序列比例为45%~100%; h 奇异值序列比例为50%~100%
图4a 是各道模拟微地震记录所构建的分解矩阵对应的时间延迟量τ曲线。分解矩阵其它参数用公式(9)求取。图4b是由第一道模拟记录所构建的分解矩阵经过奇异值分解后所对应的奇异值序列,可以看出,奇异值分布呈现明显的阶梯状。其中,前3个数值较大的奇异值主要对应分解矩阵中各道相关性较强的强周期干扰;数值居中的奇异值(序号为4~70)主要对应强周期干扰和微地震有效信号;数值较小的奇异值主要对应随机干扰(序号为71~126)。单道SVD去噪就是通过选取有限个数值居中的奇异值进行矩阵重构(带通滤波),以达到削弱强周期干扰和随机干扰的目的。由于每道模拟记录构建的分解矩阵经奇异值分解后对应的奇异值序列不同,为了更合理地讨论奇异值选取原则,剖面重构奇异值选取采用百分比形式进行描述。图4c是采用数值较大奇异值重构后的剖面,可以看出,较大奇异值主要对应微地震记录中周期性较强的噪声。图4d,图4e和图4f是采用中间不同范围奇异值进行重构的剖面,可见,采用中间部分奇异值进行剖面重构可较好地突出有效信号。图4g和图4h是采用数值较小的奇异值进行重构的剖面,可以看出,较小奇异值主要对应微地震记录中的随机噪声,对有效信号的重构贡献不大。但在图4g 中隐约呈现出有效信号同相轴的影子,因此可将45%定为奇异值序列的上限比例。由模拟结果可见,参与剖面重构奇异值序列比例下限以大于6%为宜,上限以小于45%为宜,选取10%~45%内的奇异值进行重构可有效压制周期干扰。
2.1.2 振幅比理论模型测试
图5a是振幅比法理论模型,模型在200~600ms含有一条呈双曲线规律分布的同相轴,与此同时,在模型中加入能量较强的随机噪声。下面采用振幅比法对该模型数据进行处理。
图5b至图5e是采用不同尺寸时窗振幅比法进行去噪后的重构剖面。其中,扩展时窗长度均为固定时窗的2倍。从重构效果可以看出,当固定时窗长度为20ms时(图5b),原始模型中随机噪声得到较好压制,但有效信号也受到较大程度的削弱。固定时窗长度为40ms时(图5c),有效信号得到更好的突出,同相轴的连续性有所增强。当固定时窗长度增加到100ms时(图5d),有效信号的同相轴基本得到恢复,但在200~400ms出现能量较强的随机干扰。当固定时窗长度增大到200ms时(图5e),有效信号得到完全重构,随机噪声得到较好压制。图5f是固定时窗为200ms时,第一道模拟记录对应的R′(n)曲线。从曲线图可以看出,第100个采样点处R′(n)值较大,由于剖面采样间隔为2ms,该点正好对应剖面中第一道记录200ms位置,与实际情况相符。从理论模型实验可以看出,固定时窗长度增加到200ms时,随机噪声得到有效的压制,有效信号得到了较好的突出。可见,振幅比法是一种压制随机噪声,突出有效信号的去噪方法。

图5 理论模型及振幅比法重构结果a 振幅比法理论模型;b 固定时窗长度20ms,扩展时窗40ms;c 固定时窗长度40ms,扩展时窗80ms; d 固定时窗长度100ms,扩展时窗200ms;e 固定时窗长度200ms,扩展时窗400ms;f 第一道模拟记录R′(n)曲线(固定时窗长度200ms)
2.1.3 联合去噪理论模型测试
图6a为联合去噪方法的理论模型。模型在200ms有一条水平同相轴,在400~700ms含有一条呈双曲线规律分布的同相轴。
为验证联合去噪方法的有效性,在模型的单道记录中加入强周期干扰,在整体模型中加入能量较强的随机噪声。图6b是采用振幅比法(固定时窗长度200ms)去噪后的重构剖面,可以看出,原始剖面中的随机干扰得到较好的压制,但单道模拟记录中的强周期干扰依然较为严重。图6c是采用单道SVD方法(重构奇异值序列比例为15%~45%)去噪后的重构剖面,可见,原始剖面单道记录中的强周期干扰得到较好压制,但剖面中的随机干扰仍然较为严重。图6d是联合去噪后的重构剖面,可以看出,联合去噪方法同时压制了模拟记录中的强周期干扰和随机干扰,资料的信噪比得到明显改善,这也说明本文的联合去噪方法是一种有效的微地震资料去噪方法。
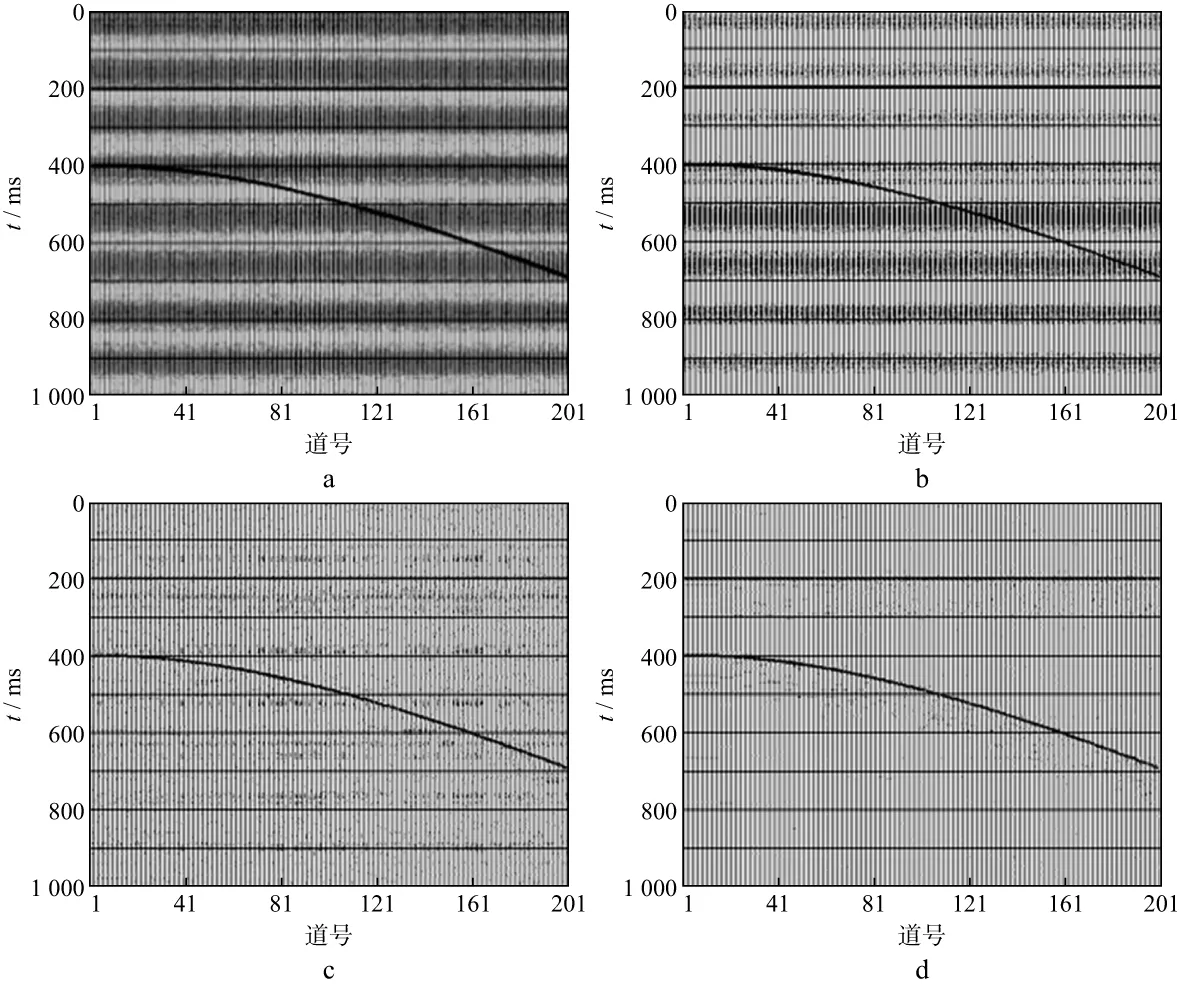
图6 理论模型及不同固定时窗下模型重构剖面a 含噪声的理论模型数据; b 固定时窗长度200ms的振幅比重构剖面; c 奇异值序列比例为15%~45%的单道SVD重构剖面; d 联合去噪后重构剖面(参数同b和c)
2.2 实际微地震资料处理
2.2.1 单道SVD应用于实际资料处理
图7为四川某地区地面微地震射孔资料剖面,图中椭圆内的同相轴为直达波同相轴。图中可见能量较强的噪声干扰使得直达波同相轴无法得到较好的突出。观察单道微地震记录可以看出,噪声的周期性较强,这为单道SVD去噪方法提供了前提条件。因此,可采用单道SVD去噪方法对微地震资料进行去噪处理。此外,参与剖面重构的奇异值采用百分比形式进行选取。
图8是利用单道SVD选取不同范围奇异值重构后的结果。其中,图8a是各道微地震记录所构建的分解矩阵对应的时间延迟量τ曲线,分解矩阵其它参数按公式(9)求取。图8b是由第一道微地震记录所构建的分解矩阵经奇异值分解过后所对应的奇异值序列。与模拟记录相比,实际微地震资料奇异值数值变化相对平缓,这说明实际微地震资料强周期干扰没有理论模型明显。
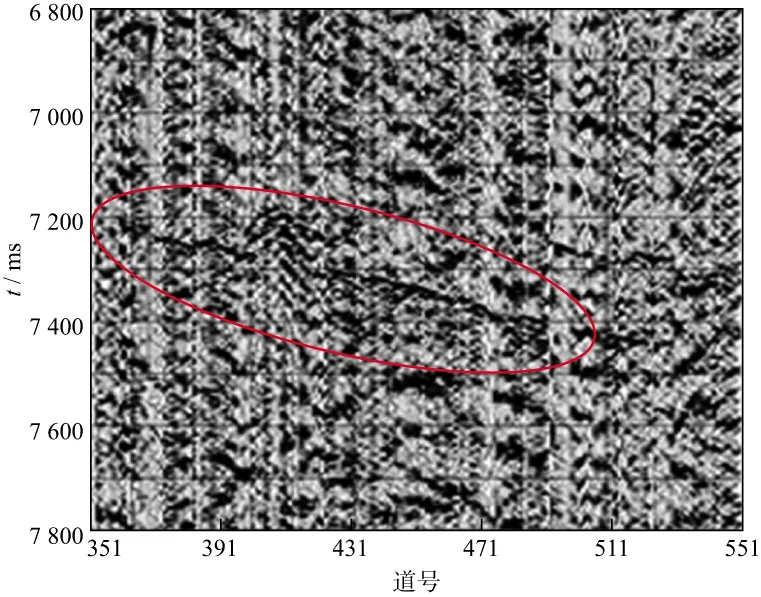
图7 四川某地区地面微地震射孔资料剖面
图8c是选取奇异值序列前5%数值较大奇异值进行重构后的剖面,从重构效果可以看出,主要对应低频强周期干扰。图8d和图8e分别是选取奇异值序列比例大于38%和大于36%的数值较小奇异值进行重构的剖面。对比图8d和图8e可以看出,图8d主要对应原始微地震剖面中的随机干扰,而从图8e中却隐约可见有效直达波的信息。所以,在进行微地震资料重构时,可将参与剖面重构奇异值序列比例上限定为36%。
图8f,图8g和图8h分别为采用不同范围中间部分奇异值进行重构的剖面,可以看出,当奇异值序列比例上限为36%时,剖面重构效果随着参与重构奇异值比例下限的增大得到明显改善;当下限值达到15%时,重构效果较为理想,强周期干扰和随机干扰都得到较好的压制。可见,选取序列比例为15%~36%的奇异值进行重构时,微地震剖面信噪比可得到较大程度的改善。
综上所述,对于实际的微地震资料,参与重构的奇异值序列比例以下限大于5%,上限小于36%为宜。通常情况下,选取序列比例为15%~36%的奇异值进行微地震资料重构。
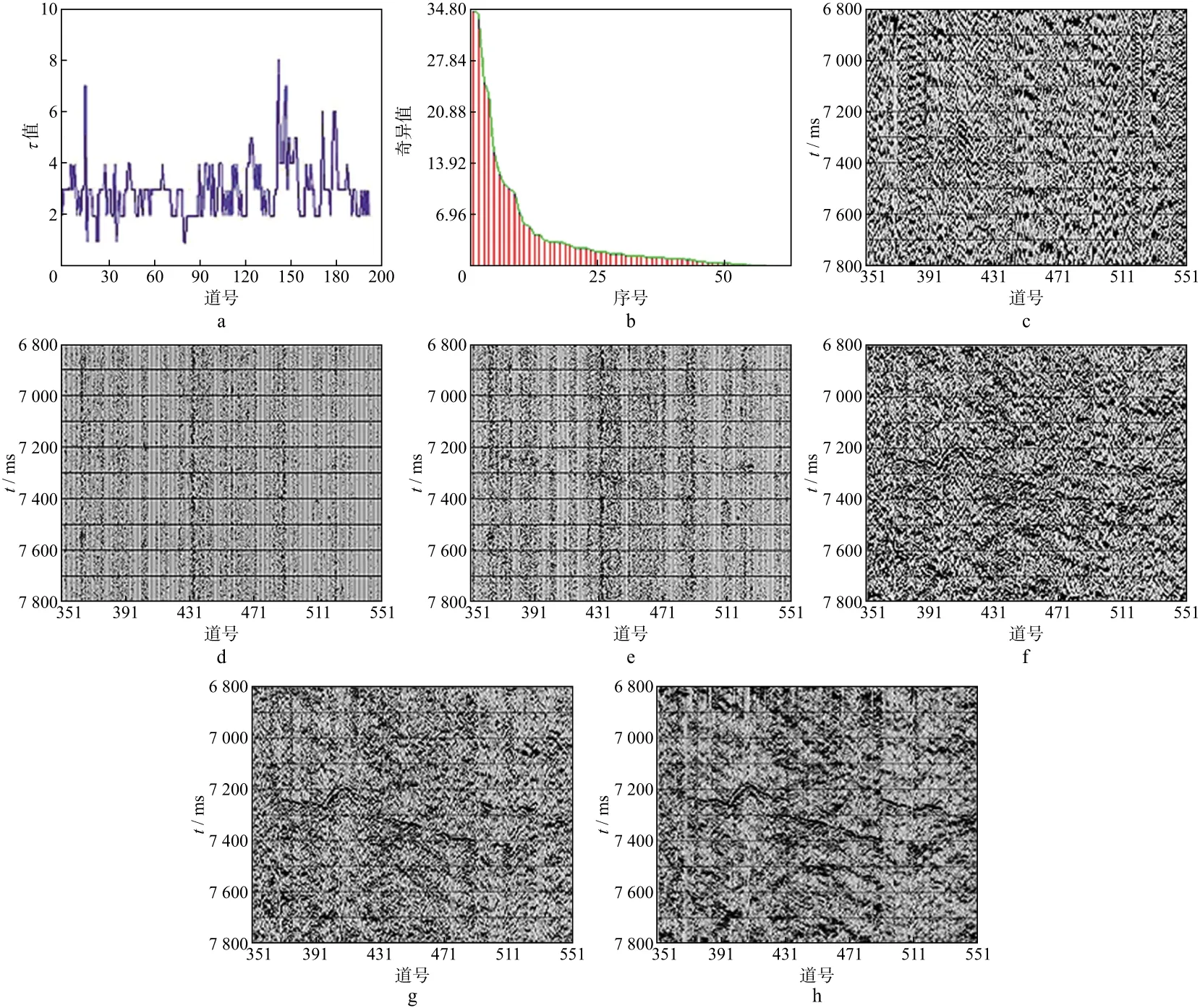
图8 单道SVD去噪重构剖面a 各分解矩阵对应时间延迟量τ曲线; b 第一道微地震记录构建的分解矩阵对应的奇异值序列; c 奇异值序列比例<5%; d 奇异值序列比例>38%; e 奇异值序列比例>36%; f 奇异值序列比例为5%~36%; g 奇异值序列比例为12%~36%; h 奇异值序列比例为15%~36%
2.2.2 振幅比应用于实际资料处理
为验证振幅比法的有效性,我们采用振幅比法对微地震射孔资料(图7)进行处理。图9是采用不同尺寸固定时窗的振幅比法进行去噪后的微地震资料重构剖面,可以看出,固定时窗长度在小于40ms范围内变化时,原始剖面中噪声得到较好的压制,尤其是能量较强的低频随机噪声,并且随着时窗长度的增加,微地震有效信号的同相轴连续性有所增强;当固定时窗长度增加到100ms时,尽管有效信号同相轴连续性得到进一步改善,但低频随机噪声能量也有所增强(图9c);当固定时窗长度增加到200ms时,低频噪声已经相当严重(图9d中红色矩形框区域)。经分析可知,采用振幅比法进行微地震资料处理时,固定时窗长度不宜过长。针对四川地区地面微地震资料,固定时窗长度在40~100ms取值可以得到较好的去噪效果。
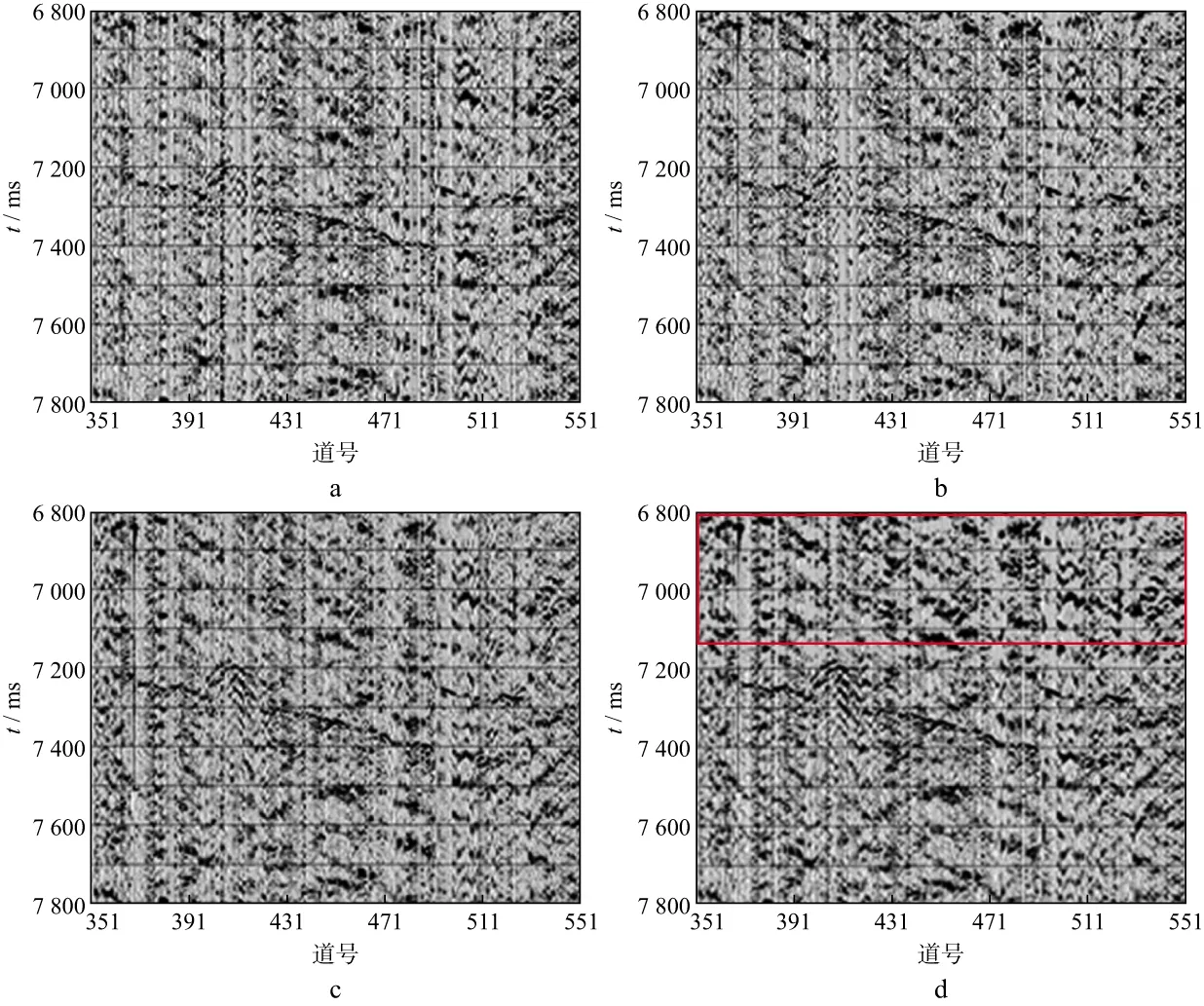
图9 不同固定时窗下振幅比法资料重构剖面a 固定时窗长度20ms,扩展时窗长度40ms; b 固定时窗长度40ms,扩展时窗长度80ms; c 固定时窗长度100ms,扩展时窗长度200ms; d 固定时窗长度200ms,扩展时窗长度400ms
2.2.3 联合资料处理
图10是采用单道SVD和振幅比联合去噪方法对地面微地震射孔资料(图7)去噪后的重构剖面。首先采用振幅比法(固定时窗80ms,扩展时窗160ms)压制微地震资料中的随机噪声,减少随机噪声对单道SVD方法的影响;然后采用单道SVD方法(奇异值序列比例取值为15%~36%)压制单道微地震记录中的强周期干扰。
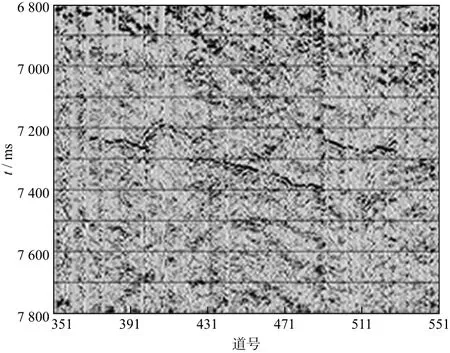
图10 单道SVD与振幅比联合去噪微地震资料重构剖面
从重构效果可见,联合去噪方法充分发挥了两种去噪方法的优势,同时压制了强周期性干扰和随机干扰,使微地震资料信噪比得到较大程度的改善。这也说明,对于地面微地震资料而言,联合去噪是提高资料信噪比的一种有效手段。
3 结论
本文在已有地面微地震资料去噪方法的基础上,提出基于单道SVD和振幅比的联合去噪方法,实现对压制微地震资料中的强周期性噪声和随机噪声的压制,提高了信噪比。将此方法应用于模型数据和四川某地区地面微地震射孔资料,在很大程度上改善了单一去噪方法无法有效突出有效信号的不足,进一步说明了联合去噪方法是改善地面微地震资料信噪比的有效手段。此外,由于单道SVD方法需进行矩阵构建、分解、重构等一系列计算,尽管采用了内存优化手段,计算效率不是十分理想。在后期实践中,将GPU计算、分布式计算等技术应用于联合去噪方法是提高算法效率的主要研究方向。

