回转窑模型与智能控制研究

艾 红，邵婷婷

(北京信息科技大学自动化学院，北京 100192)

0 引言

水泥回转窑系统是不断进行输入/输出的高温复杂系统，它的热工参数众多，物理反应、化学反应复杂交错，且系统反应中气、固、液三相并存。对水泥回转窑生产系统的主要环节(分解炉和回转窑的内部生产过程)进行分析，针对分解炉的温度变化和回转窑的温度变化，找出影响它们各自温度变化的主要因素。水泥生产系统很复杂，生产过程具有多变量、非线性、强干扰、大滞后等特点，给准确建立模型带来很大难度；利用某水泥厂监测得到的数据，采用辨识工具箱对水泥回转窑系统进行模型研究。良好的回转窑模型不仅会使水泥高质量生产，而且能够降低能源和资源的消耗率，减少对环境的污染。温度是影响水泥生产质量的主要因素之一。一个更为接近实际的回转窑模型，在对其进行温度控制时，控制效果会较好，误差会较小。回转窑系统是一个具有非线性、时变性和多变性的复杂系统，以往的常规控制并不能取得很好的控制效果。在计算机飞速发展的今天，计算机技术为智能控制的实现提供了保障，智能控制技术广泛应用于各种复杂的工业过程中，能够实现以往常规控制所不能实现的自动控制。智能控制对回转窑复杂系统的控制具有较大的优越性[1-3]。

1 水泥生产工艺与回转窑

新型干法水泥回转窑系统工艺流程如图1所示。回转窑是水泥生产过程的关键设备，生料从窑烟房的进料托盘送入窑壳内，由于窑壳的倾斜和缓慢旋转，物料产生既沿着窑筒体圆周径向翻滚，又沿着轴向窑筒体从高部向低部移动作复合运动。原料在窑内进行分解和煅烧，水泥熟料烧制完成后从窑壳下端排出，进入冷却机运行后续工艺流程。燃料从窑头注入并在窑炉内部燃烧，释放的热量加热原料，将原料煅烧成熟料。与物料进行热交换后形成的热空气从进料炉喷入窑尾系统，最后从烟囱排入大气。

图1 系统工艺流程图

回转窑的水泥生产工艺主要由四部分组成：生料磨、煤磨、水泥磨和回转窑。生料磨主要是研磨生料，把生料细化可以加快燃烧速度，并且使反应更充分进行，不仅释放更多热量，还可以节省生料的使用。煤磨原理与其相同。生料在水泥窑中煅烧成熟料后经过水泥磨的研磨即可制成水泥成品，其主要生产过程如下。

首先是生料的制作工艺。生料是经过生料制备系统生成的。生料制备系统由生料的原料和研磨生料的粉磨组成。生料的原料主要为：石灰石、砂岩、铁粉、矿渣。这四部分原料想要组成水泥还得考虑计算它们的比例关系。配比完成后，通过给料机把生料送往生料磨研磨成粉状，研磨好的生料再通过提升机输送到生料分配器。分配器主要对生料进行均化。均化好的生料再通过生料计量系统由气力泵输送到回转窑内煅烧成熟料[4-5]。

从生料配比完到输送到回转窑内煅烧成熟料的过程还需要经过许多步骤。均化完的生料先通过气力泵输送到五级旋风式预热器内。五级旋风式预热器能充分预热生料，为煅烧节省了时间，也节省了能源。经过充分预热的生料再进入分解炉进行受热发生化学反应，最后再进入回转窑，从回转窑的窑头和窑尾喷入的煤粉与生料在一起不断受热充分燃烧发生化学反应，直至生成熟料。熟料生成后要经过篦冷机冷却，再送入熟料库。此时，回转窑内产生的废气会由窑尾废气处理系统进行处理，尽量保护环境还会对废气的余热进行充分利用。

除了生料的制作过程，还有很重要的一种物质制作那就是煤粉制作。煤粉的制作主要由原煤经过煤磨磨成煤粉制成，煤粉制成后不会立即输送到分解炉和回转窑中，而是会存放在煤粉仓中，预热生料，再输送煤粉。煤粉的输送主要靠喂煤系统组成。经过回转窑煅烧后的水泥只是初级水泥。初级水泥还要经过水泥粉磨系统研磨，并配以石膏再输送至水泥磨，才能制成最终的水泥[6-7]。

2 回转窑选取的主要参数

①分解炉温度。

一般分解炉出口温度需要达到850～900 ℃才能顺利地进行烧结反应。它反映了分解率、煤粉燃烧条件、风量是否合适以及进口通道是否堵塞等。如果温度过高，表明燃料添加过多或燃烧缓慢，炉内温度过高可能导致窑炉系统过热结皮，甚至引起堵塞；如果炉温过低，则意味着分解炉的底部燃料用尽。

②窑尾温度。

一般窑尾温度控制在950～1 100 ℃，常用热电偶或辐射高温计测量。它与烧成带温度、预热系统温度一起，表征窑内及窑外热力分布情况，反应窑内燃料供给量及总热量，反应生料的易烧性、火焰长短和煤粉的燃烧状况。由于进窑温度大约为850 ℃，如果窑尾温度保持低温，将使窑末段失效、窑内平均温度下降，对窑内传热和化学反应是不利的。同时，控制窑尾温度过低限制了窑炉的通风和加热能力，影响了高温带的长度并且减少了可以传递到预热器中材料的热量。

③窑头喷煤反馈(即喂煤量)。

喂煤量对煅烧区域的温度和废气中的氧气含量有着直接影响。增加喂煤量可以提供煅烧区域温度并降低氧气含量，减少喂煤量可以降低煅烧区域温度并增加氧气含量。当回转窑运行稳定时，喂煤量应与进入窑炉的物料量相平衡，因此必须与窑转速保持平衡。

④生料量。

增加物料会引起温度降低，物料太多则会导致物料反应不充分，影响水泥产出的品质和产量。当窑速剧烈变化时，喂料量应随之调整，最好与窑速成一定比例以保持窑内料层均匀，这样利于克服干扰因素。

⑤窑主电机电流。

窑内炉料多，主电机运行电流整体上升；窑内结圈、窑口结渣不均匀，甚至是炉料发黏翻动效果差都会引起主电机电流周期性变化。主电机电流是整个回转窑运行负载的直接体现。当窑内出现大量结皮，出现前圈、后圈、大料球时，窑主电机电流增大。当出现跑生料时，窑主电机电流减小。

⑥回转窑转速。

回转窑转速应基本保持不变。当窑速变化较大时，应相应调整进料量，最好与窑速保持一定比例，以维持窑料层均匀。这样有助于克服干扰因素。

从某大型水泥厂实际生产过程中获得的整点数据中选取合适水泥生产的参数。与回转窑相关的常用数据如表1所示。

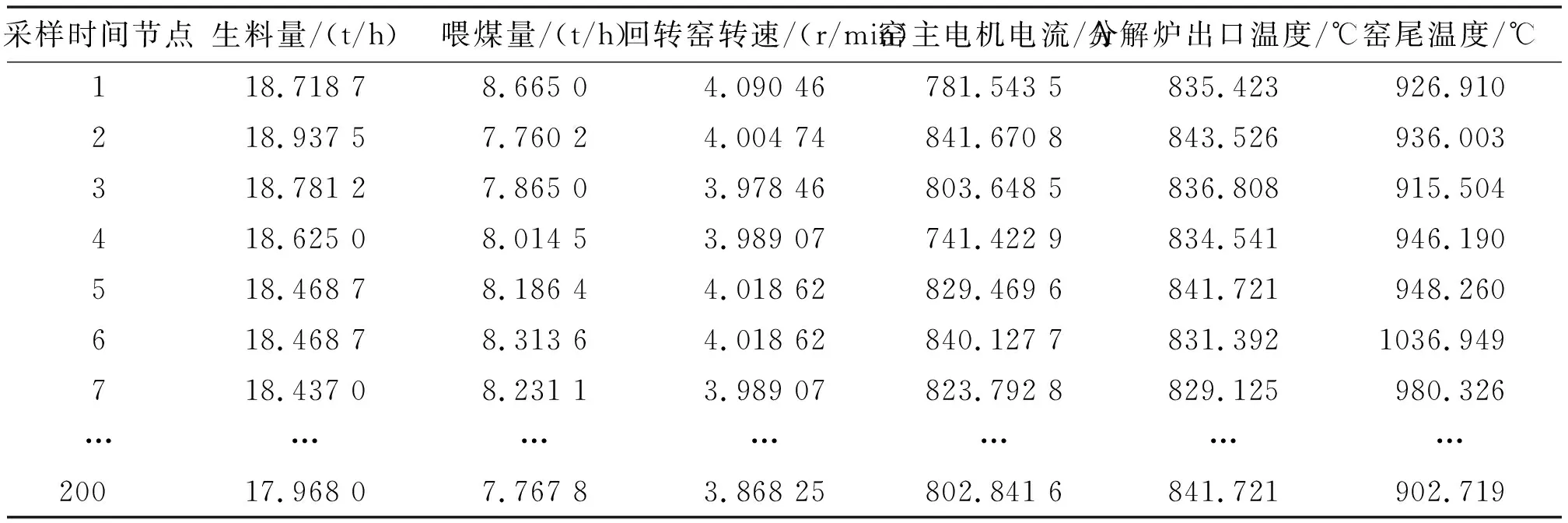
表1 与回转窑相关的常用数据

3 模型参数辨识

参数辨识是在已经确定模型结构的前提下通过实际操作获取系统输入输出数据辨识求取模型参数，通常辨识结果为传递函数。增大喂煤量和生料量，将升高分解炉温度；减少喂煤量和生料量，将降低分解炉温度[8-9]。回转窑炉体采用保温隔热材料建造，当氧含量变化窑内温度升高时，窑内的空气会进行对流换热(即热交换)，窑体会吸收一部分热量，增加窑内的温度。由于回转窑炉的尺寸和质量较大，表现出一定的惯性滞后，并且输出对输入控制量的变化响应缓慢，类似于一阶惯性对象的输出特性，因此，用一阶惯性和延迟环节来近似模拟窑尾温度输出和控制量之间的传递函数关系，如式(1)所示。

(1)

式中：对象的特性用时间常数T、纯滞后时间τ、广义对象放大系数K三个参数描述。

首先，导入数据至MATLAB工作区间。在MATLAB命令行窗口输入ident调出模型辨识工具箱，将数据导入到MATLAB系统辨识工具箱中。代入生料量和窑尾温度的数据，点击Process Models运行得到参数：Kp=47.251、Tp1=21.299、Td=0.388。

通过辨识，生料量与窑尾温度之间传递函数为：

(2)

喂煤量与窑尾温度之间传递函数为：

(3)

喂煤量和窑尾温度这两组数据辨识出的二阶振荡滞后模型，其传递函数为：

(4)

生料量与分解炉温度之间的传递函数为：

(5)

喂煤量与分解炉温度之间的传递函数为：

(6)

回转窑转速与分解炉温度之间的传递函数为：

(7)

回转窑转速与窑尾温度之间的传递函数为：

(8)

以生料量和分解炉温度之间通过数据辨识出的模型为例，将其传递函数输出到工作区间并勾选Model output。辨识模型拟合曲线如图2所示。

图2 辨识模型拟合曲线

从图2可以看出，辨识模型拟合曲线能较好地跟踪实际测量变量的输出曲线。因此，由模型辨识工具箱辨识出的模型具有一定可信度。

4 模糊控制及模糊PID控制

4.1 窑尾温度模糊控制器设计

模糊控制器结构如图3所示。

图3 模糊控制器结构图

在每个输入输出语言变量的量化论域中，定义模糊子集。该设计中模糊子集设置为{负大，负中，负小，零，正小，正中，正大}七个元素的序列，模糊语言记为：{NB,NM,NS,ZR,PS,PM,PB}。由于回转窑温度的变化较为平缓，温度偏差隶属度函数取为高斯函数，其形式为：

(9)

4.2 建立模糊推理系统

在MATLAB环境中，使用模糊推理系统编辑器和隶属度函数编辑器。选定适合输入输出模糊变量的量化论域范围以及选定模糊语言变量的隶属度函数类型等关键参数，选用默认的重心法作为解模糊方法，完成模糊推理系统中相关变量的定义和各变量隶属度函数的选择设定。在MATLAB的应用程序中点击Fuzzy Logic Designer，进入模糊逻辑工具箱。在Edit中添加输入输出变量至设计控制器所需要的数量，双击input或output修改控制器变量名称，并设置量化论域的范围。在Current Membership Function中设置模糊子集和各隶属度函数。

4.3 模糊控制仿真研究

对于回转窑模糊控制系统，可以利用Simulink对其进行仿真。经过反复比较和验证，PID的三个控制参数分别选取为kP=80、ki=9、kd=80,模糊控制变量量化因子ke、kec的取值大小对控制系统的动态性能如响应时间和超调量等有很大影响。当ke偏大时，系统超调量较大，响应时间长过渡过程缓慢。当kec较大时，超调量将减小，kec选择越大超调量越小，对超调的抑制作用十分明显，但系统的响应速度变慢，应当在两个动态性能间选定最适宜的量化因子取值。量化因子ke、kec的取值大小意味着对输入变量偏差和偏差变化趋势的不同加权程度，ke、kec这两个因素之间也相互影响。模糊控制系统的特性也受到输出比例因子ku的影响。ku选择过小会使得系统动态响应过程缓慢，过渡过程变长，而ke=0.4、kec=5、ku=5。

仿真运行时，需调整Simulation中的Model Configuration Parameters参数。将Solver改为ode23s，将Zero-crossing control改为不予允许，避免因仿真过程中的数据因迭代次数过高而运行时间过久，并将Diagnostics进行稍微调整。利用Simulink设计模糊PID，模糊控制和PID控制三种控制方案，控制对象选定喂煤量和窑尾温度这两组数据辨识出的二阶振荡滞后模型，其传递函数为：

(10)

搭建Simulink模型后，点击模糊控制器，分别设置为“purefussy”和“fussypid”，连接模糊推理系统。仿真时间为 100 s 时，模糊PID及模糊控制仿真结果如图4所示。由图4可以看出，模糊控制鲁棒性强， 适用于解决过程控制中的非线性、强耦合时变、滞后等问题。对纯模糊控制器超调量小但调节时间过长快速性较差且存在静差，系统控制精度降低动态品质变差。虽然模糊PID控制的结构复杂，但优化控制效果明显，超调量较小、上升时间短、系统响应速度快、调节时间短、稳态性能好、动态性能稳定，充分体现了模糊PID 参数自整定调节参数的效果。

图4 模糊PID及模糊控制仿真结果图

4.4 加干扰信号后的控制方案仿真结果

由于回转窑稳定工作时的窑尾温度在890 ℃左右，所以在程序运行零时刻加入给定的信号890 ℃，运行40 s后加入幅值为+90 ℃的干扰。加干扰信号后的控制方案仿真结果如图5所示。

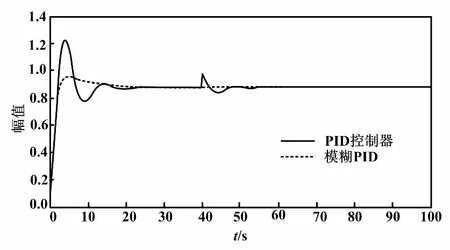
图5 加干扰后的控制方案仿真结果图

从图5可以看出，在加干扰之后，模糊PID控制能快速且小超调地稳定到初始信号设定值，PID控制调节时间较长，且对于出现扰动时的恢复时间同样较长，快速性较差，超调过大。模糊PID控制能快速克服扰动且超调量小，动态性能较好。

5 模糊PID控制用M文件编写

控制对象选定喂煤量和窑尾温度这两组数据辨识出的二阶振荡滞后模型，传递函数为：

(11)

将模糊PID控制以M文件的形式写出，主要程序是使用语句a=newfis(' fuzzypid')建立新的模糊推理规则，继而设定输入及输出变量的量化论域及隶属度函数形如a=addvar(a,'input','e',[-3 3]);addmf(a,' input',1,' NM',' trimf' )等。

再将连续系统的传递函数用Z变换离散化，并求出其零极点矩阵，如下所示。

sys=tf(5.798,[905.107 98.182 1],'inputdelay',0);

dsys=c2d(sys,ts,' tustin');

//连续系统离散化，用z变换

[num,den]=tfdata(dsys,' v');

//求零极点矩阵

语句k_pid=evalfis([0.4*e_1,5*ec_1],a)利用编辑好的模糊推理工具箱对系统实际输出偏差和偏差变化率进行基于模糊逻辑的控制。其中，将偏差e的量化因子和变化率ec的量化因子分别设置为0.4和5。并将模糊控制输出后的结果保存在k_pid这个矩阵内部。

模糊PID控制及PID控制运行结果如图6所示。

图6 模糊PID控制及PID控制结果图

6 结束语

选出影响水泥回转窑分解炉及窑尾温度的变量，根据某水泥厂获得的实际生产过程中各个测控参数的数据及回转窑系统自身的特点，利用辨识工具箱进行操作，得到与水泥回转窑煅烧系统各测量和控制参数对应的辨识模型，确定对象的传递函数。基于模糊集理论、模糊语言知识表示和模糊逻辑规则推理，采用模糊控制和模糊PID控制自动整定参数并实现温度控制。将MATLAB中的模糊推理工具箱及可视化Simulink模型相结合，对模糊控制系统的控制进行有效的实现。通过仿真运行结果比较PID控制、模糊控制和模糊PID控制的控制效果。比较结果表明，模糊PID控制效果理想，鲁棒性强，适用于水泥回转窑锻烧系统的温度控制。