基于超声声速的气力输送颗粒体积分数测量

安连锁，刘伟龙，魏 萌，林 冲，沈国清，张世平

(华北电力大学能源动力与机械工程学院，北京 102206)

0 引言

气力输送由于具有密封性好、输送量大、输送距离长等特点，被广泛应用于众多工业过程中。颗粒体积分数作为气力输送过程中的重要参数之一，科研工作者已经研发了多种测量体积分数的方法，研究较多的方法包括电容法[1]、静电法[2]、光学法[3]、声学法[4]。其中，超声法以其良好的穿透性等优点，得到业界越来越多的关注。目前，研究较多的就是超声衰减情况，而声速相关的论文鲜有报道。

许伟龙[5]等对电站锅炉颗粒介质中的可听声频段的声速进行了数值研究，分析了部分参数对其声波传播的影响。其研究表明，在仅改变浓度的情况下，声速随着浓度的增大而减小。乔榛[6]曾对声速随着颗粒粒径、浓度、超声频率的变化进行了理论分析。研究结果表明，在一定范围内，颗粒的粒径和超声频率对声速的影响均可忽略不计。刘心志[7]等采用均相模型作为参考模型，利用超声声速对气粉混合物的浓度进行了测量，证明声速法可以作为一种测量颗粒相浓度的有效手段。李永明[8]等利用基于多重散射理论的超声计算模型对管道内粉体体积分数进行了测量。测量结果表明，声速法对体积分数更为敏感，但其并未将试验结果与其模拟结果进行对比。

本文利用基于两相流理论的Harker和Temple[9-10]模型，对气力输送过程中的超声声速法测量颗粒相的浓度进行了理论分析。通过分析部分参数对声速测量的影响，推导了超声声速与颗粒相体积分数的关系，证明了理论与实际的结果相近。该方法可以应用于实际生产中颗粒相体积分数的测量。

1 理论基础

超声波在气固两相流中传播过程中，由于气体和固体颗粒的物理性质不同，会发生吸收、散射耗散等现象。造成超声波的能量和速度变化的主要原因如下。

①替代效应：由于两种介质的密度不同，其声速的传播速度会发生变化。

②黏性损失：超声波本质上是一种机械波，由于两相间的密度差异，颗粒相在振动过程中会对气相产生相对滑移。

③热损失：由于两相的导热系数和传热系数不同，会在两相交界面产生温度梯度。一些学者[11-12]从声波传播角度出发，建立了能够准确描述球形颗粒在气固两相流中的声波动的ECAH模型。该模型将声波的传播特性归结到一个6阶线性方程组并进行求解，得到由声速和声衰减来表征的复波数k，由此得到其声速。另一些学者从两相流的角度出发，从质量守恒、能量守恒、动量守恒的角度来求解超声波在气固两相间的传播特性，来求解复波数k，进而求解出超声声速。本文根据Harker 和 Temple的两相流理论，预测气力输送中的超声声速c。其计算式为：

(1)

S=Q+jP

(2)

(3)

(4)

ω=2πf

(5)

(6)

2 试验系统及过程参数

2.1 试验系统

系统主要通过振动给料机配合其储料仓进行连续给料，超声信号发生器由汕头超声公司生产，能够产生20 kHz～5 MHz超声脉冲信号。管道系统由有机玻璃制造的管径为50 mm的竖直管道组成。

在管道中部截面，直径方向上相对布置一对直径为22 mm的超声换能器。下部设置回收系统，从而对颗粒进行回收。系统结构如图1所示。

图1 系统结构图

2.2 试验过程及参数

采集信号如图2所示。

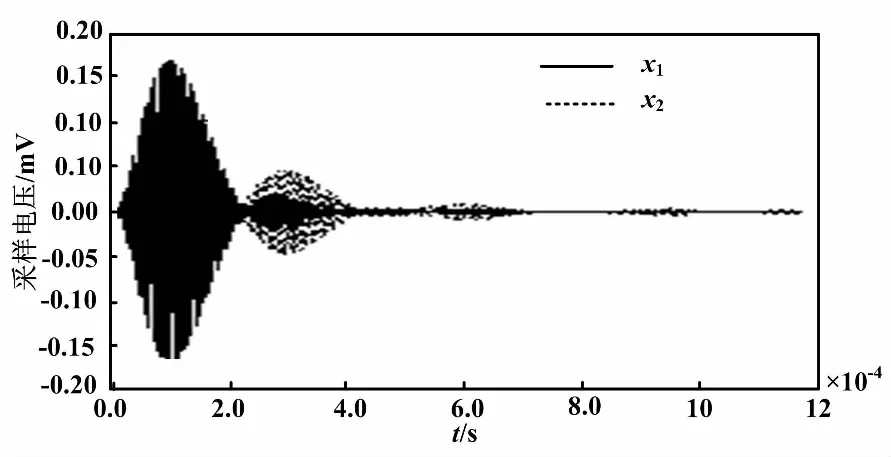
图2 采集信号图

在试验进行前，先对振动给料机进行给料量标定，通过电压调节器来调节给料机电压，进而调节给料量。在试验过程中，信号发射端的驱动频率为140 kHz，驱动电压为350 V。驱动信号驱动超声换能器产生频率为140 kHz的超声信号，超声信号通过管道后由对面的另外一个超声换能器接收，接收到的信号经过放大后经由采集卡采集到计算机中，信号发生器的信号与接收端的信号同时接入数据采集卡并进入计算机。

从图2可以看出，和发射端信号相比，接收端的信号存在时间延迟。

本文通过对发射端和接收端的信号进行互相关求取时间延迟τ，进而求取声速c。

3 模拟与试验结果分析

3.1 数值分析结果

利用Harker 和 Temple的两相流理论，对空气-玻璃微珠气力输送中的超声传播过程进行数值模拟。玻璃微珠和空气的物性参数如表1所示。

表1 玻璃微珠和空气的物性参数

声速-频率曲线如图3所示。由图3(a)可以看出，当频率大于50 kHz时，其声速不再随着频率的变化而变化。因此，在选取频率的过程中，应选取高于50 kHz的信号来作为信号源进行测量。由图3(b)可以看出，在粒径改变的情况下，当超过125 kHz时，随着频率的增大，声速趋于稳定值。

图3 声速-频率曲线

不同参数下的声速-粒径曲线如图4所示。由图4(a)可以看出，当粒径在大于某个范围时，其声速趋于平稳状态。100～200 μm时声速的变化在该范围内，其声速也是趋于平稳状态。本文所采用的 180 μm的粒径范围内， 颗粒粒径变化对声速的影响可以忽略不计。由图4(b)可以看出，在固定浓度的情况下，当粒径大于某个范围时，其声速处于稳定值。

图4 声速-粒径曲线

通过以上对参数的分析可知，利用频率在140 kHz的超声信号，可以实现声速法测量颗粒体积分数。

在试验过程中，玻璃微珠样品的平均直径为180 μm。图5给出了在此条件下超声声速-颗粒体积分数的关系。由图5可见，随着颗粒体积分数的增大，超声波声速逐渐减小。

图5 声速-体积分数曲线(R=180 μm,f=140 kHz)

3.2 声速法颗粒浓度结果

试验结果与理论值存在相同的趋势，随着体积分数的变化，声速逐渐减小。而试验值略高于理论值，分析其影响因素主要有以下几点。

①温度的影响。在理论计算中，并未涉及温度对声速的影响，而在试验过程中，温度对声速产生的影响是不能忽略的。

②颗粒分布的影响。在理论计算中，假设气相和颗粒相是均匀分布的。而在试验过程中，由于其气力输送属于湍流状态，难以实现理想状态下的均匀状态。在流动过程中，局部浓度不均会对其超声传播造成影响。声速-体积分数结果对比如图6所示。

图6 声速-体积分数结果对比图(R=180 μm,f=140 kHz)

4 结束语

通过理论推导出超声声速与颗粒相体积分数的关系，并对理论分析结果和试验结果进行对比，理论结果与试验结果基本吻合。由此说明，对于低浓度的气力输送过程，Harker 和 Temple的两相流理论的声速法可以用来对其体积分数进行测量。在获得其颗粒相密度的前提下，本文所采用的方法为颗粒相的体积分数测量提供了一种行之有效的手段。