氧化石墨烯/丁苯橡胶复合材料力学性能的分子动力学模拟

孙 斌， 郭 伟， 顾建兵， 米立伟

(中原工学院 材料与化工学院，河南 郑州 451191)

0 引 言

近年来，碳基纳米填料如碳纤维、碳纳米管、石墨烯等广泛地应用到聚合物复合材料的力学改性中.其中，氧化石墨烯(graphene oxide, GO)作为一类新型的纳米填料，越来越受到研究人员的关注[1-2].氧化石墨烯是石墨烯的衍生物，和纯石墨烯相比，它含有许多官能团，如羧基、羟基、羰基等.这些含氧官能团的存在，使得氧化石墨烯片能够很好地分散在水和聚合物基质中，并且能够保留材料的力学性能[3].

丁苯橡胶是应用最广泛的通用橡胶品种，广泛应用于轮胎、胶带、电线电缆、医疗器具等领域[4].但到目前为止，关于氧化石墨烯/丁苯橡胶纳米复合材料体系的研究非常少.笔者利用分子动力学模拟和ReaxFF反应力场，考察了氧化石墨烯/丁苯橡胶纳米复合材料的拉伸性能、硬度和耐摩擦性能.和Frankland、Chawla等[5-6]的研究相比，笔者的研究的创新之处有两个方面.一方面是使用Aryanpour等[7]开发的ReaxFF反应力场，它能够准确的模拟化学反应中键的生成和断裂.大量的研究表明，ReaxFF反应势函数在模拟聚合物体系力学性能方面具有较高的准确性[8].另一方面是使用氧化石墨烯作为增强材料，而不是石墨烯或氢功能化石墨烯.

1 计算方法

1.1 模型的建立

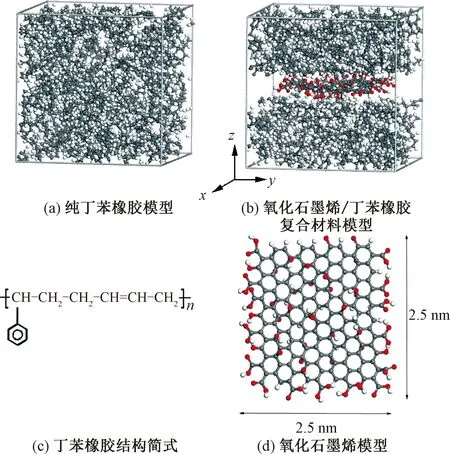
图1 计算模型Fig.1 Calculation model

1.2 单轴拉伸模拟

分子动力学模拟软件Lammps具体的模拟步骤如下：模型建立后,首先利用共轭梯度法对模型进行能量最小化处理,再利用Nose-Hoover热浴法控制体系在室温293 K下弛豫50 ps达到平衡态, 同时控制体系各方向上压力为1个大气压.对弛豫后的模型沿y轴方向施加均匀的拉伸应变，应变率为1×108/s,每次应变为0.000 1，每加载一次应变后弛豫5 000步, 分子动力学模拟的时间步长为0.10 fs,即弛豫时间为0.50 ps.重复此加载和弛豫过程, 直到应变达到60%.在拉伸过程中只对拉伸方向(y轴)设置周期性边界, 其他方向 (x轴和z轴)为自由边界.体系应力的计算使用的是维里应力计算方法[11]：

(1)

式中：i、j表示应力的方向；α、β代表原子序号；m和v分别是原子α的质量和速度；rαβ和Fαβ分别代表原子α和β之间的距离和力；V是系统总体积；N是体系内的原子个数.

1.3 硬度和摩擦性能的模拟

为了全面考察加入氧化石墨烯后丁苯橡胶力学性能的变化，笔者计算了纯丁苯橡胶和氧化石墨烯/丁苯橡胶复合材料两种模型的硬度和摩擦性能.采用的模拟方法见参考文献[7],具体模拟步骤如下：首先建立了铁针-丁苯橡胶-铁块模型，如图2所示.在图2中，最上面的是铁针，尺寸为0.40 nm×0.40 nm×2 nm.中间是构建好的纯丁苯橡胶模型，见图2(a)，氧化石墨烯/丁苯橡胶复合材料模型,见图2(b).这里的纯丁苯橡胶和复合材料模型已经进行过1.2节所述的能量最小化和弛豫平衡处理.图2中的最下层是铁块，尺寸为3.50 nm×3.50 nm×1 nm.在模拟中，各个方向均采用周期性边界条件.

在进行硬度模拟时，对铁针沿-y方向施加3个大小不同的冲击载荷，分别是0.12、0.24和0.36 kJ/(mol·nm).然后测量铁针压入丁苯橡胶中的深度，把此作为压痕深度h.

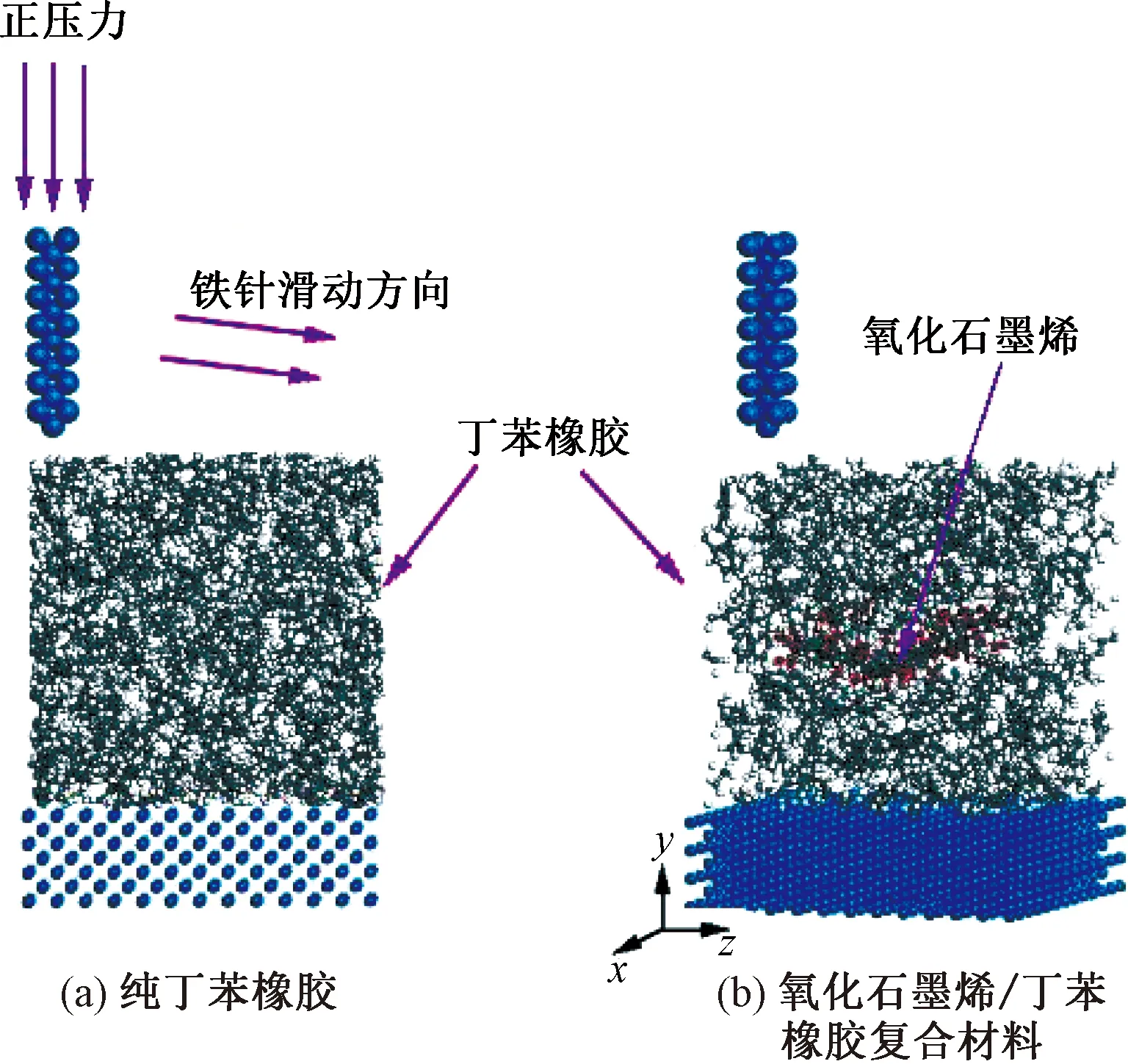
图2 用于硬度和摩擦力计算的铁针-丁苯橡胶-铁块3层模型胶复合材料Fig.2 A three-layer model of iron needle-SBR-iron block for hardness and friction calculation

在进行摩擦性能模拟时，首先将铁针沿-y方向缓慢移动到聚合物表面，对铁针施加一定的正压力使铁针同时向-y方向和z方向移动，移动速度分别是0.000 1 nm/fs和0.000 25 nm/fs.在移动过程中，记录下铁针最顶部原子的受力(fx、fy、fz)，根据公式μ=F/N(μ为摩擦系数，F为摩擦力，N为正压力)计算出摩擦系数.摩擦过程结束后，由于吸附作用，铁针会将一部分丁苯橡胶分子链带走，依据带走的分子链的多少，可以计算出磨损率I:

I=NFe/Ntot,

(2)

式中:NFe是被铁针带走的碳原子数量;Ntot是摩擦之前橡胶中碳原子的总数.

笔者还计算了摩擦过程中丁苯橡胶和氧化石墨烯之间结合能的变化，计算公式如下：

Uint=Utot-UGO-USBR,

(3)

式中:Uint为氧化石墨烯和丁苯橡胶之间的结合能;Utol为氧化石墨烯/丁苯橡胶复合材料的势能;UGO为氧化石墨烯的势能;USBR为丁苯橡胶的势能.

2 结果与讨论

2.1 拉伸性能

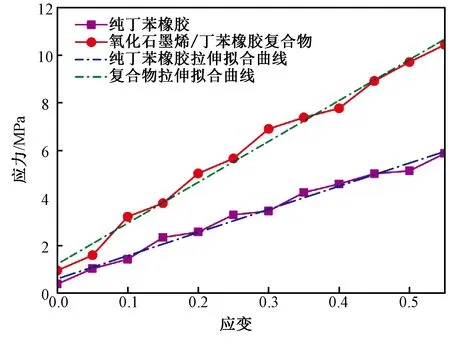
图3 纯丁苯橡胶和氧化石墨烯/丁苯橡胶复合材料的应力-应变曲线Fig.3 The stress-strain curves of pure SBR and GO/SBR composites

图3是纯丁苯橡胶和复合材料两种模型的应力-应变曲线.由于应力波动较大，我们对两条曲线进行了线性拟合.从图3可以看出，加入氧化石墨烯后，复合材料的杨氏模量明显增大.纯丁苯橡胶的杨氏模量为9.80 MPa，而氧化石墨烯/丁苯橡胶复合材料的杨氏模量达到17.30 MPa.相比于纯丁苯橡胶，复合材料的杨氏模量提高了77%.图3的结果与其他实验及计算机模拟的结果是一致的[6,12].一般认为，氧化石墨烯的增强机制主要是氧化石墨烯的比表面积特别大，达到2 600 m2/g.如此大的表面积使得氧化石墨烯与聚合物基体的接触面积也很大，结合能很强，这使得应力能够很好地从基体传递到氧化石墨烯,从而增大了聚合物链抵抗变形的能力.此外，这种结合作用也限制了聚合物链的局部运动，进而阻止了聚合物基体中裂纹的产生和扩展[13].

2.2 硬度计算

利用1.3节所述的模拟方法，笔者计算了两种模型的硬度.表1是纯丁苯橡胶和氧化石墨烯/丁苯橡胶复合材料在不同载荷下的压痕深度h.可以看出，两种模型的的压痕深度h均随载荷的增大而增加.当载荷从0.12 kJ/(mol·nm)增加到0.36 kJ/(mol·nm)，纯丁苯橡胶压痕深度从0.162 nm增加到1.057 nm，氧化石墨烯/丁苯橡胶复合材料的压痕深度从0.123 nm增加到0.871 nm.这表明添加氧化石墨烯后，复合材料的硬度增大，压痕深度比纯丁苯橡胶的平均减小20.3%.

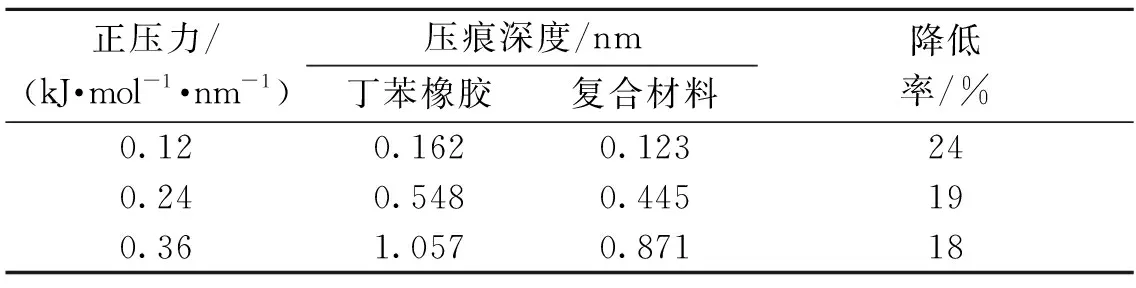
表1 纯丁苯橡胶和氧化石墨烯/丁苯橡胶复合材料在不同载荷下的压痕深度Tab.1 The indentation depth of pure SBR and GO/SBR composite under different loads

2.3 摩擦性能

依据橡胶摩擦性能测试的原理，笔者建立了铁针-丁苯橡胶-铁块3层模型来计算不同体系的摩擦性能，包括摩擦系数、磨损率等.此外，还考察了摩擦过程中氧化石墨烯和丁苯橡胶之间结合能和氢键能的变化以及铁原子(铁针中的铁)-碳原子(丁苯橡胶和氧化石墨烯/丁苯橡胶中的碳)的径向分布函数(RDF)，以此来考察氧化石墨烯和丁苯橡胶间的相互作用机制.

图4(a)和(b)分别是铁针摩擦过纯丁苯橡胶和氧化石墨烯/丁苯橡胶后的模型快照图.如1.3节所述，根据摩擦力公式μ=F/N，通过记录摩擦过程中铁针顶端原子在3个方向上的受力fx、fy、fz，我们可以计算摩擦系数μ.这里，|fy|等于正压力N，|fz|等于摩擦力F.计算结果见表2.需要说明的是，表2给出的摩擦系数是不同阶段摩擦系数的算术平均值，即当t=1、2、3、4、5、6、7、8、9、10、11、12 ps时，计算摩擦系数，然后求算术平均值.表2还给出了两种不同模型的磨损率.

图4 纯丁苯橡胶和氧化石墨烯/丁苯橡胶摩擦后的3层模型快照Fig.4 After friction processthree-layer model snapshot of pure SBR and GO/SBR

材料摩擦系数μ磨损率I/%纯丁苯橡胶0.5520.00复合材料0.4512.40

从表2可以看出，加入氧化石墨烯后，复合材料的摩擦系数和磨损率分别降低了18%和38%,这说明加入氧化石墨烯后，丁苯橡胶的耐磨损性能增强.为了考察氧化石墨烯对丁苯橡胶基体摩擦性能增强的机理，笔者计算了摩擦过程中氧化石墨烯和丁苯橡胶之间结合能的变化，如图5所示.

图5 摩擦过程中氧化石墨烯和丁苯橡胶之间的结合能Fig.5 The variation of interaction potential energy between GO nanosheet and SBR matrix during the course of friction process

从图5可以看出，在摩擦过程中，氧化石墨烯和丁苯橡胶基体间的结合能从463.45 kJ/mol增加到867.18 kJ/mol，增加了87%.也就是说，当材料受到摩擦力作用后，聚合物链和氧化石墨烯之间发生了更多的吸附作用或其他的非键相互作用，从而使整个体系达到更稳定的状态.在Chawla等[6]的研究中，所用的增强填料为石墨烯，研究表明这种相互作用是电磁力和范德华力.而在笔者的研究中，由于氧化石墨烯含有大量的含氧官能团，所以除了电磁力和范德华力之外，氧化石墨烯中的氧原子极有可能会和丁苯橡胶中的氢原子形成氢键.为了验证这种假设，我们计算了摩擦过程中氧化石墨烯和丁苯橡胶间氢键能的变化，如图6所示.从图6可以看出，随着摩擦时间的增加，氢键能逐渐增大，从28.7 kJ/mol增大到89.3 kJ/mol,其主要原因是由于铁针产生的压力使氧化石墨烯分子和丁苯橡胶分子链距离更近，产生更多的氢键，从而氢键能增大.据此可以得出，在摩擦过程中，丁苯橡胶与氧化石墨烯间结合能增加的原因之一是氢键作用的增强.

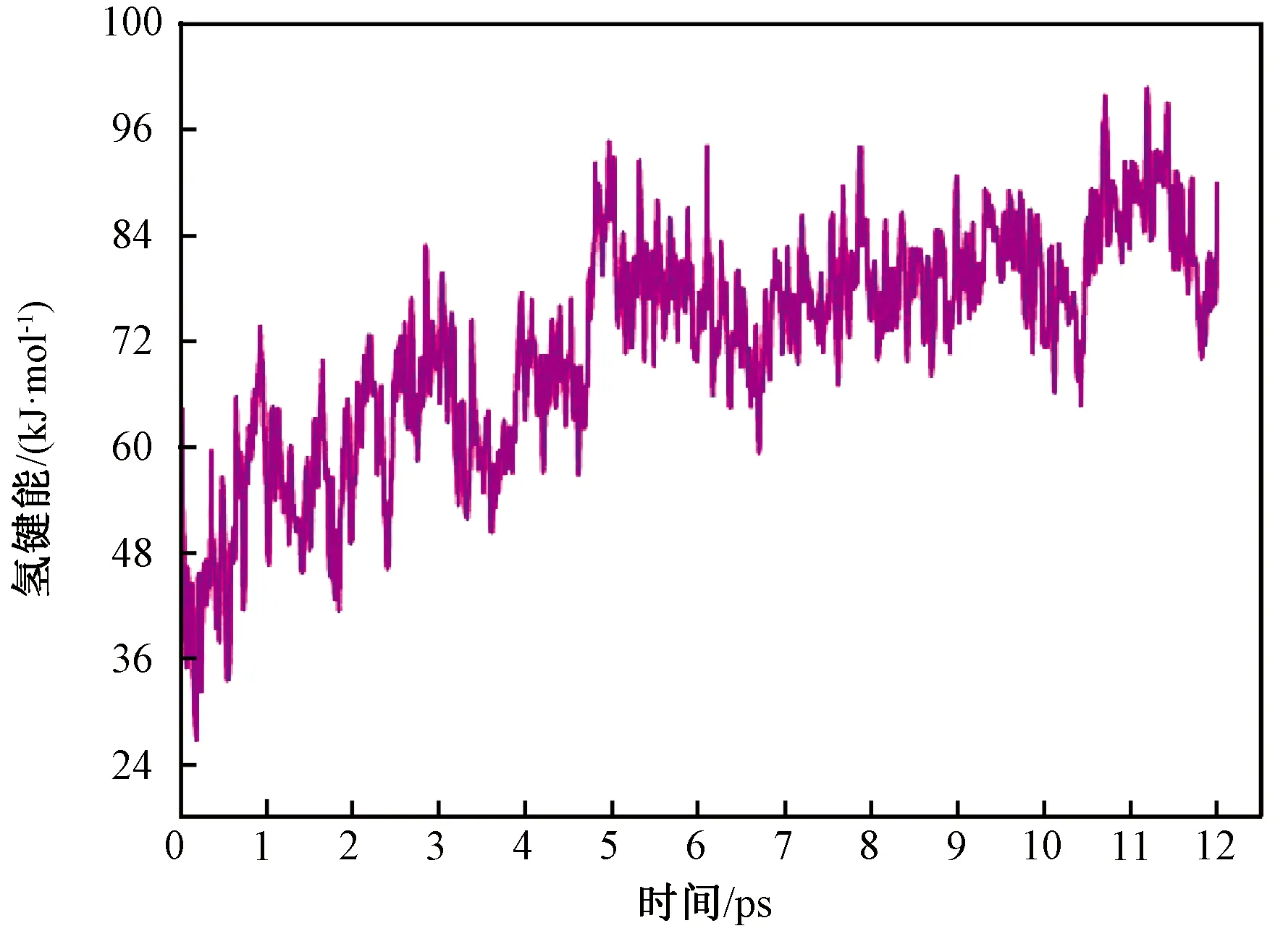
图6 摩擦过程中氧化石墨烯和丁苯橡胶之间氢键能的变化Fig.6 The variation of hydrogen bond energy between GO and SBR during the course of friction process

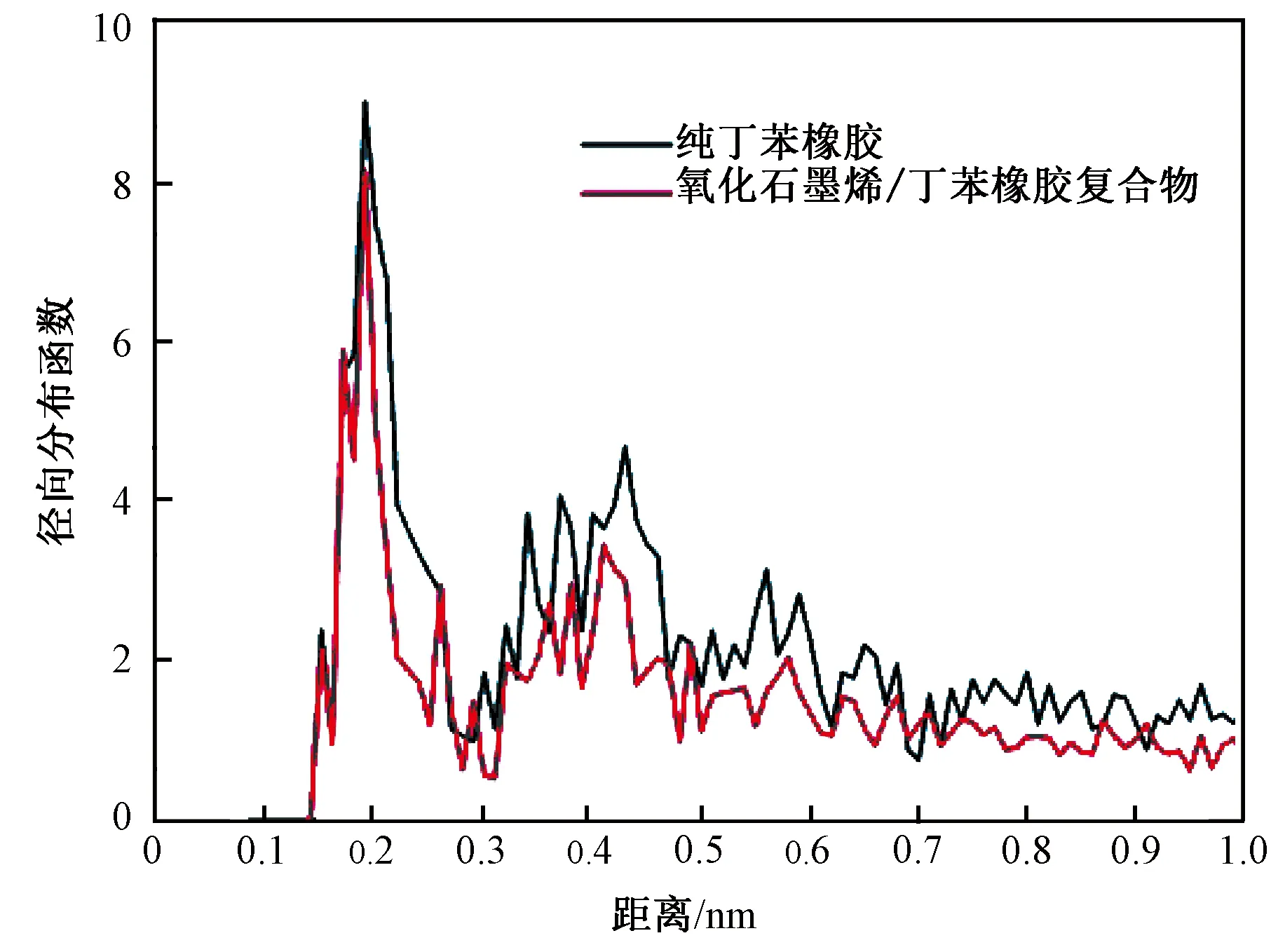
图7 铁针中的铁原子和丁苯橡胶及氧化石墨烯/丁苯橡胶复合材料中碳原子间的径向分布函数Fig.7 Radius distribution function between iron atoms in the iron needle and carbon atoms in the pure SBR or GO/SBR composites

笔者还计算了摩擦过程结束后，即图4(a)和4(b)铁针中的铁原子和丁苯橡胶及氧化石墨烯/丁苯橡胶复合材料中碳原子间的径向分布函数(RDF)，结果见图7.从图7可以看出，纯丁苯橡胶的RDF值要略高于复合材料的，这说明在氧化石墨烯/丁苯橡胶复合材料中，和铁棒发生吸引作用的丁苯橡胶分子要少一些.这个结论也可以很直观地从图4(a)、(b)看出.这个结果也再次证明，加入氧化石墨烯后，丁苯橡胶基体和氧化石墨烯之间发生了更多非键相互作用和氢键作用，导致基体和填料间结合能的增加，这也正是氧化石墨烯/丁苯橡胶复合材料摩擦性能增强的微观机理.

3 结论

笔者利用分子动力学模拟和ReaxFF反应力场，研究了加入氧化石墨烯后丁苯橡胶的力学性能及其增强机理.单轴拉伸模拟表明，加入氧化石墨烯后，复合材料的杨氏模量比纯丁苯橡胶提高了77%.并建立了铁针-丁苯橡胶-铁块3层模型，考察了复合材料的硬度和摩擦性能.计算结果表明，加入氧化石墨烯后，复合材料的硬度提高20.30%，摩擦系数和磨损率分别降低18.20%和38%.笔者还计算了摩擦过程中氧化石墨烯和丁苯橡胶之间结合能及氢键能的变化，提出了摩擦性能增强的机理.在摩擦过程中，丁苯橡胶基体和氧化石墨烯之间的结合能逐渐增大，结合能增大其中的一个原因是氢键作用的增强.结合能的增大使得应力能够很好地从丁苯橡胶基体转移到强度更高的氧化石墨烯上，从而提高复合材料的耐摩擦性能.